文档内容
2023-2024 学年秋学期高三年级期初调研考试
数学学科试卷
时间: 120分钟 满分:150分
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1. 已知集合 , ,则 ( )
.
A B. C. D.
2. 已知复数 , 则 ( )
A. B. C. D.
3. 已知等比数列 的前 项和为 ,且 , , 成等差数列,则数列 的公比 (
)
A. 1或 B. 或 C. D.
4. 若双曲线 的焦距为6,则该双曲线的离心率为( )
A. B. C. 3 D.
5. 向量旋转具有反映点与点之间特殊对应关系的特征,在电子信息传导方面有重要应用.平面向量旋转公
式在中学数学中用于求旋转相关点的轨迹方程具有明显优势,已知对任意平面向量 ,把 绕
其起点沿逆时针方向旋转 角得到向量 ,叫做把点B绕点A沿逆时针
方向旋转 角得到点P.已知平面内点 ,点 ,把点B绕点A沿顺时针方向旋转
第1页/共6页
学科网(北京)股份有限公司后得到点P,则点P的坐标为( )
.
A B. C. D.
6. 已知 ,则 ( )
A. B. C. D.
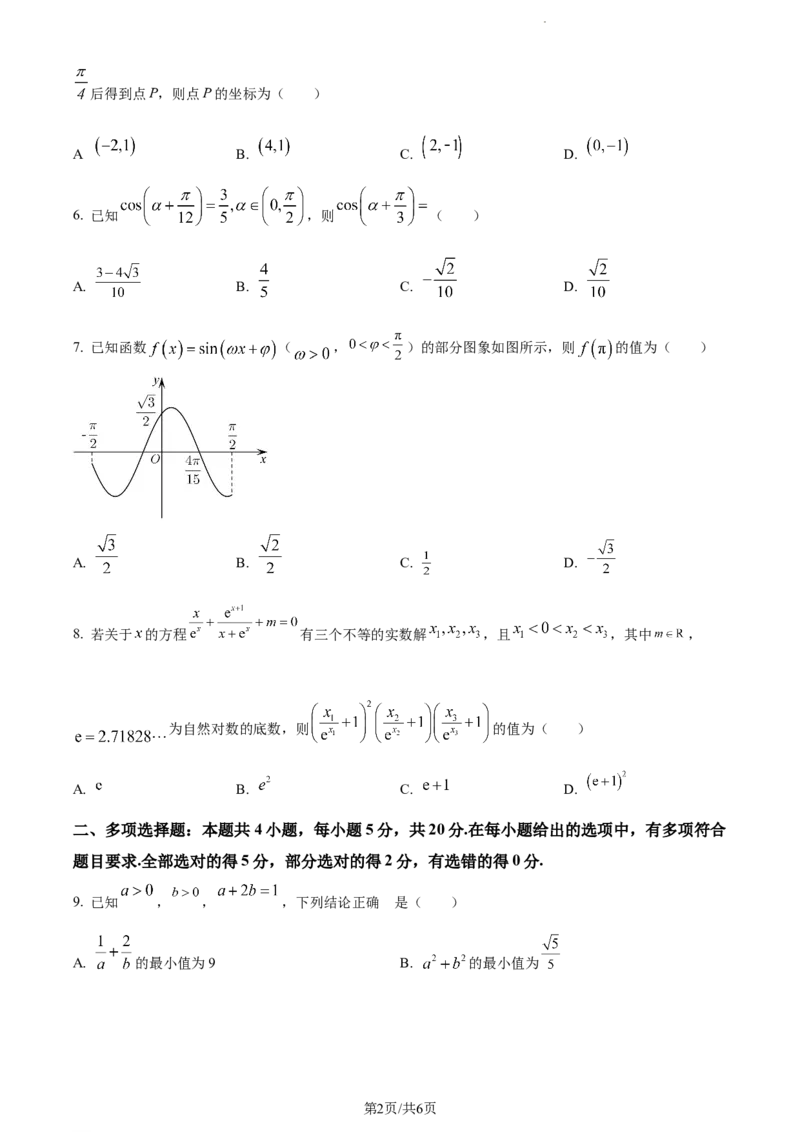
7. 已知函数 ( , )的部分图象如图所示,则 的值为( )
A. B. C. D.
8. 若关于 的方程 有三个不等的实数解 ,且 ,其中 ,
为自然对数的底数,则 的值为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
的
9. 已知 , , ,下列结论正确 是( )
A. 的最小值为9 B. 的最小值为
第2页/共6页
学科网(北京)股份有限公司C. 的最小值为 D. 的最小值为
10. “天宫课堂”是为发挥中国空间站的综合效益,推出的首个太空科普教育品牌.为了解学生对“天宫课堂”
的喜爱程度,某学校从全校学生中随机抽取200名学生进行问卷调查,得到以下数据,则( )
不喜欢天宫课
喜欢天宫课堂
堂
男生 80 20
女生 70 30
参考公式及数据:① , .②当 时,
.
A. 从这200名学生中任选1人,已知选到的是男生,则他喜欢天宫课堂的概率为
B. 用样本的频率估计概率,从全校学生中任选3人,恰有2人不喜欢天宫课堂的概率为
C. 根据小概率值 的独立性检验,认为喜欢天宫课堂与性别没有关联
D. 对抽取的喜欢天宫课堂的学生进行天文知识测试,男生的平均成绩为80,女生的平均成绩为90,则参
加测试的学生成绩的均值为85
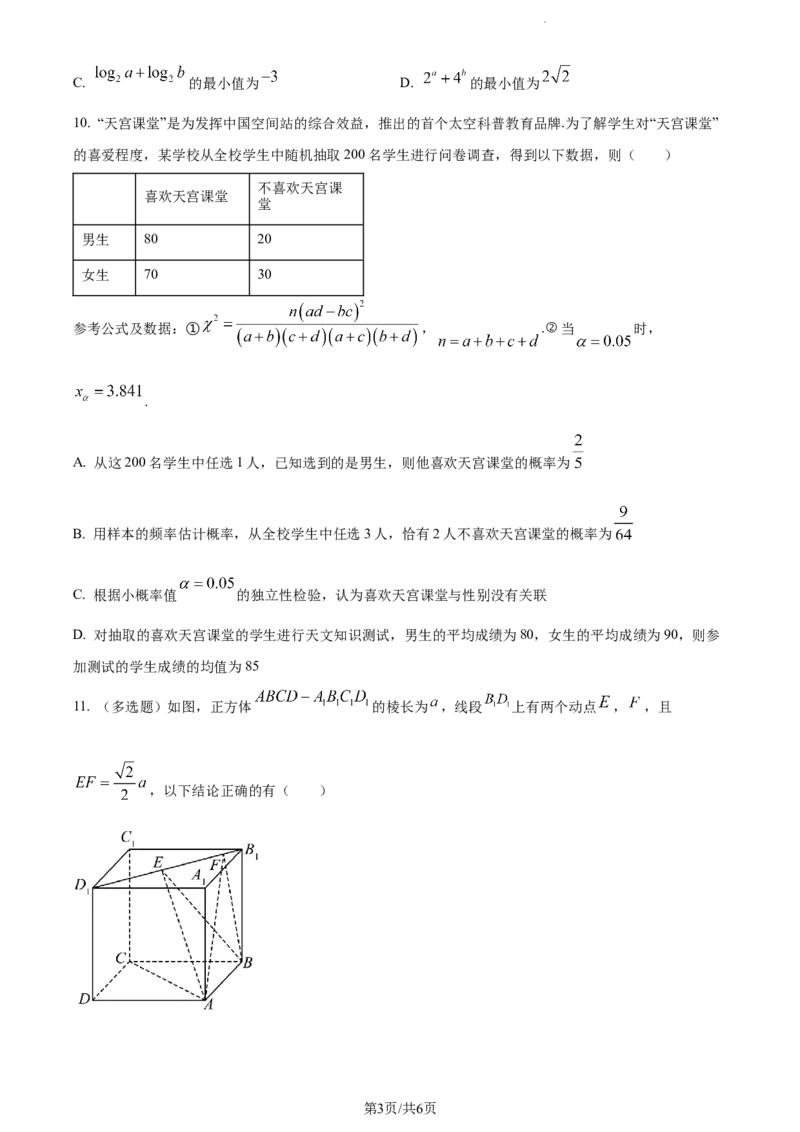
11. (多选题)如图,正方体 的棱长为 ,线段 上有两个动点 , ,且
,以下结论正确的有( )
第3页/共6页
学科网(北京)股份有限公司A.
的
B. 点 到平面 距离为定值
C. 三棱锥 的体积是正方体 体积的
D. 异面直线 , 所成的角为定值
12. 已知 ,则( )
A. B. C. D.
三、填空题:本题共4小题,每小题5分,共20分.
13. 已知“ ”是假命题,则实数 的取值范围为________.
14. 数据 的第25百分位数是__________.
15. 已知随机变量 ,其中 ,则
___________.
16. 定义在实数集 上的偶函数 满足 ,则 ____________.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 在 中,
(1)求 ;
(2)若 的面积为 ,求 的周长.
18. 已知等差数列 和等比数列 满足 .
(1)求数列 和 的通项公式;
第4页/共6页
学科网(北京)股份有限公司(2)记 ,求数列 的前 项和 .
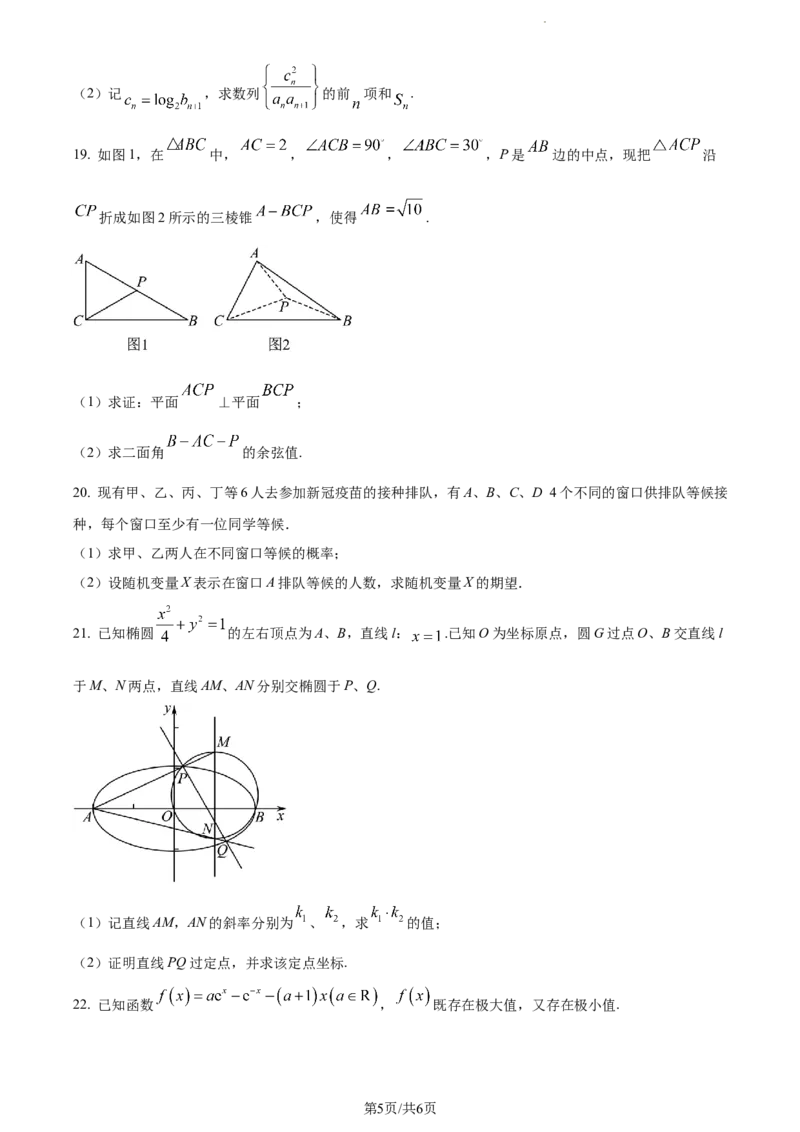
19. 如图1,在 中, , , ,P是 边的中点,现把 沿
折成如图2所示的三棱锥 ,使得 .
(1)求证:平面 ⊥平面 ;
(2)求二面角 的余弦值.
20. 现有甲、乙、丙、丁等6人去参加新冠疫苗的接种排队,有A、B、C、D 4个不同的窗口供排队等候接
种,每个窗口至少有一位同学等候.
(1)求甲、乙两人在不同窗口等候的概率;
(2)设随机变量X表示在窗口A排队等候的人数,求随机变量X的期望.
21. 已知椭圆 的左右顶点为A、B,直线l: .已知O为坐标原点,圆G过点O、B交直线l
于M、N两点,直线AM、AN分别交椭圆于P、Q.
(1)记直线AM,AN的斜率分别为 、 ,求 的值;
(2)证明直线PQ过定点,并求该定点坐标.
22. 已知函数 , 既存在极大值,又存在极小值.
第5页/共6页
学科网(北京)股份有限公司的
(1)求实数 取值范围;
(2)当 时, 、 分别为 的极大值点和极小值点,且 ,求实数 的取
值范围.
第6页/共6页
学科网(北京)股份有限公司