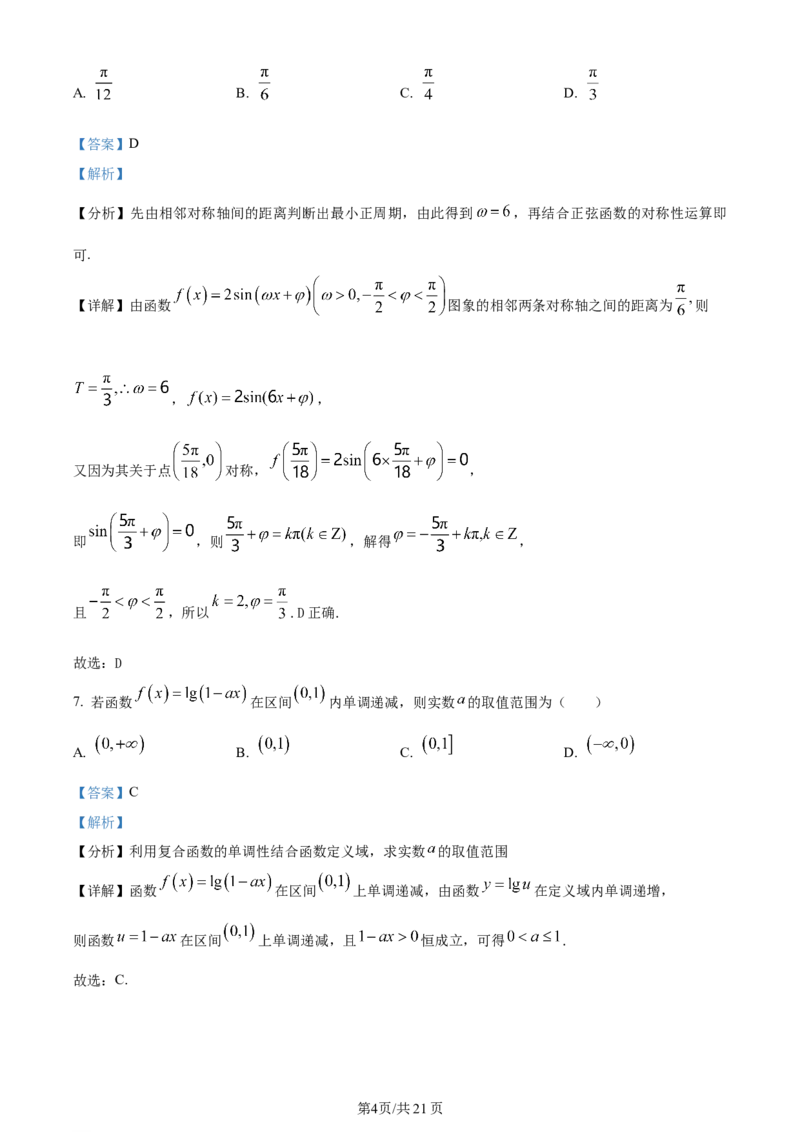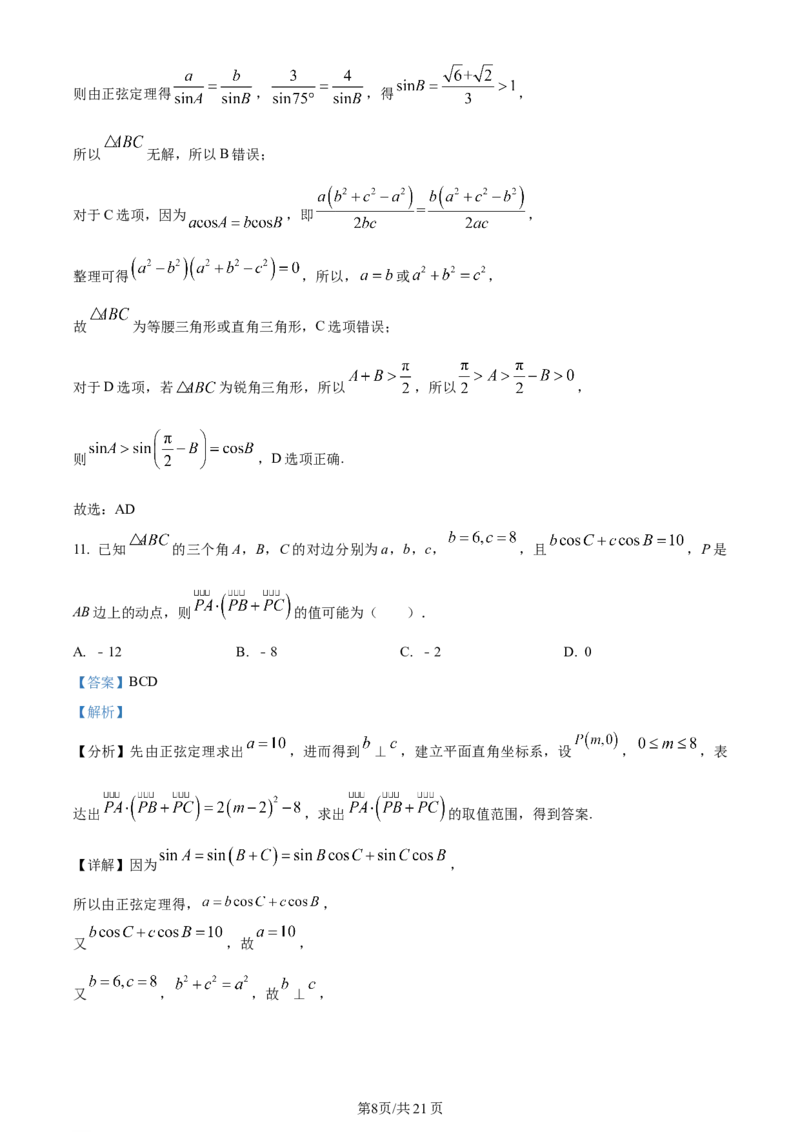文档内容
2023—2024 学年度上学期高三年级 10 月月考试题
数学
第Ⅰ卷选择题(共60分)
一、选择题:(本大题共8小题,每小题 5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的)
1. 已知集合 , , ,则实数 的值为( )
A. B. C. D.
【答案】A
【解析】
【分析】由题设知 ,讨论 、 求a值,结合集合的性质确定a值即可.
【详解】由 知: ,
当 ,即 ,则 ,与集合中元素互异性有矛盾,不符合;
当 ,即 或 ,
若 ,则 ,与集合中元素互异性有矛盾,不符合;
若 ,则 , ,满足要求.
综上, .
故选:A
2. 下列函数中,是偶函数且在 上单调递减的是( )
A. B. C. D.
【答案】B
【解析】
【分析】利用基本初等函数的奇偶性及单调性,结合各选项进行判断即可.
【详解】对于A,由题意可知 的定义域为 , ,所以 是偶
第1页/共21页
学科网(北京)股份有限公司函数且在 上不是单调递减,不符合题意;故A错误;
对于B,由题意可知 的定义域为 , ,所以 是偶函数且在 上
单调递减,符合题意;故B正确;
对于C,由题意可知 的定义域为 , ,所以 是偶函数且在 上单
调递增;不符合题意;故C错误;
的
对于D, 定义域为 ,不是偶函数,不符合题意;故D错误;
故选:B.
3. 中,点 为 上的点,且 ,若 ,则 (
)
A. B. C. D.
【答案】D
【解析】
【分析】根据题意,利用向量的线性运算法则,准确化简,即可求解.
【详解】如图所示,因为 ,
由向量的线性运算法则,
可得
因为 ,所以 ,所以 .
故选:D.
第2页/共21页
学科网(北京)股份有限公司4. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚痛减
一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走378里路,第一天
健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”则该人第一天走的路
程为( )
A. 228里 B. 192里 C. 126里 D. 63里
【答案】B
【解析】
【分析】应用等比数列的求和公式可得答案.
【详解】由题意得,该人所走路程构成以 为公比的等比数列,令该数列为 ,其前 项和为 ,
则有 ,解得 ,
故选:B.
5. 已知函数 满足 ,当 时, ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】由题意可得 是以6为周期的函数,结合已知条件即可求解.
【详解】因为 ,所以 是以6为周期的函数,
所以 ,
故选:D.
6. 已知函数 图象的相邻两条对称轴之间的距离为 且关于点
对称,则φ的值为( )
第3页/共21页
学科网(北京)股份有限公司A. B. C. D.
【答案】D
【解析】
【分析】先由相邻对称轴间的距离判断出最小正周期,由此得到 ,再结合正弦函数的对称性运算即
可.
【详解】由函数 图象的相邻两条对称轴之间的距离为 则
, ,
又因为其关于点 对称, ,
即 ,则 ,解得 ,
且 ,所以 .D正确.
故选:D
7. 若函数 在区间 内单调递减,则实数 的取值范围为( )
A. B. C. D.
【答案】C
【解析】
【分析】利用复合函数的单调性结合函数定义域,求实数 的取值范围
【详解】函数 在区间 上单调递减,由函数 在定义域内单调递增,
则函数 在区间 上单调递减,且 恒成立,可得 .
故选:C.
第4页/共21页
学科网(北京)股份有限公司8. 给定函数 ,若函数 恰有两个零点,则 的取值范围是( )
A. B.
C. D.
【答案】C
【解析】
【分析】由函数与方程的思想将函数 恰有两个零点转化成函数 与函数 图象有
两个交点,画出图像数形结合即可得 .
【详解】若函数 恰有两个零点,即方程 有两个不相等的实数根,
即函数 与函数 图象有两个交点,
易知 ,
令 ,解得 ,
所以当 时, ,函数 在 上单调递减,
当 时, ,函数 在 上单调递增,
所以 在 取得最小值 ,
易知当 时, ,且 时 ,
在同一坐标系下分别画出两函数图象,如下图所示:
第5页/共21页
学科网(北京)股份有限公司.
由图可知当 时,函数 与函数 图象有两个交点
故选:C
二、多项选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,
有多项是符合题目要求的.全部选对得5分,有选错的得0分,部分选对的得2分)
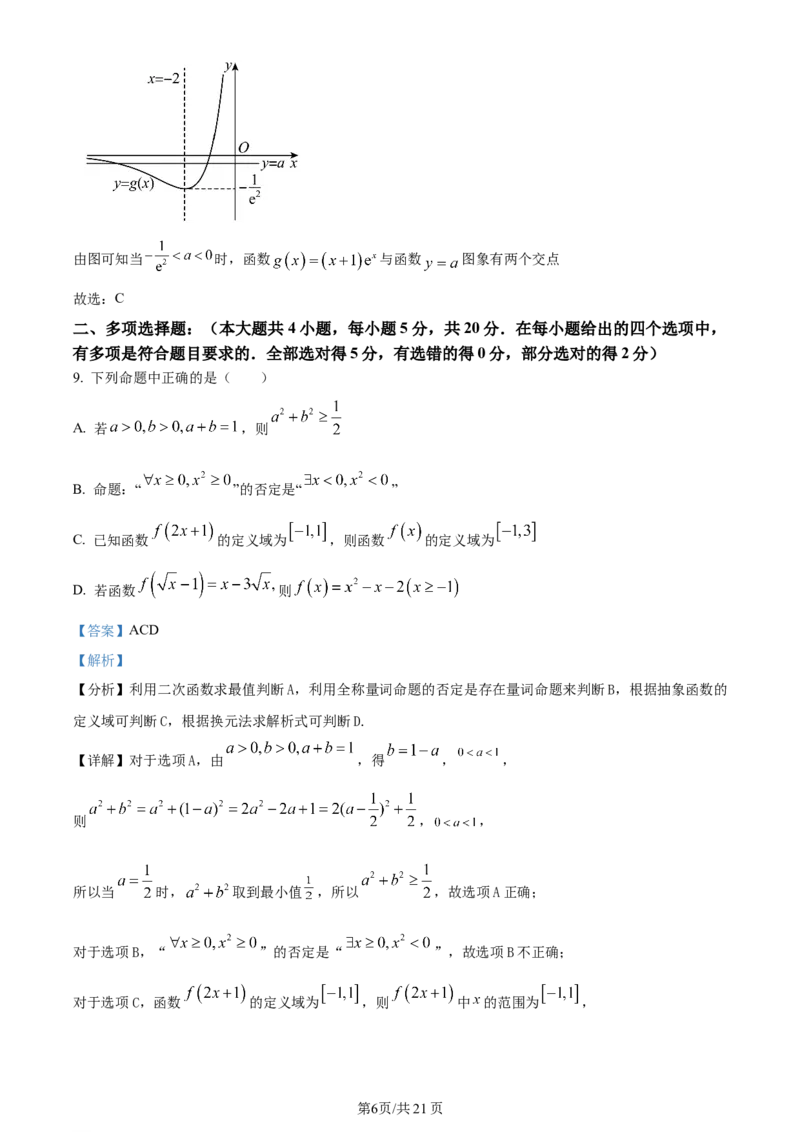
9. 下列命题中正确的是( )
A. 若 ,则
B. 命题:“ ”的否定是“ ”
C. 已知函数 的定义域为 ,则函数 的定义域为
D. 若函数 则
【答案】ACD
【解析】
【分析】利用二次函数求最值判断A,利用全称量词命题的否定是存在量词命题来判断B,根据抽象函数的
定义域可判断C,根据换元法求解析式可判断D.
【详解】对于选项A,由 ,得 , ,
则 , ,
所以当 时, 取到最小值 ,所以 ,故选项A正确;
对于选项B,“ ”的否定是“ ”,故选项B不正确;
对于选项C,函数 的定义域为 ,则 中 的范围为 ,
第6页/共21页
学科网(北京)股份有限公司即 ,所以 ,
由抽象函数的定义域可得, 中 的范围为 ,
故函数 的定义域为 ;所以选项C正确;
对于选项D,令 ,则 , ,
由 得 , ,
所以 , ,所以选项D正确.
故选:ACD.
10. 在 中,角A,B,C的对边分别为a,b,c,则下列结论正确的是( )
A. 若 ,则 一定是钝角三角形
B. 若 ,则 有两解
C. 若 ,则 为等腰三角形
D. 若 为锐角三角形,则
【答案】AD
【解析】
【分析】对于A,利用余弦定理分析判断,对于B,利用正弦定理分析判断,对于C,利用余弦定理统一
成边形式化简判断,对于D,利用正弦单调性计算判断.
【详解】对于A选项,因为 ,则 ,
故角 为钝角,A选项正确;
对于B选项,在 , , , ,
,
第7页/共21页
学科网(北京)股份有限公司则由正弦定理得 , ,得 ,
所以 无解,所以B错误;
对于C选项,因为 ,即 ,
整理可得 ,所以, 或 ,
故 为等腰三角形或直角三角形,C选项错误;
对于D选项,若 为锐角三角形,所以 ,所以 ,
则 ,D选项正确.
故选:AD
11. 已知 的三个角A,B,C的对边分别为a,b,c, ,且 ,P是
AB边上的动点,则 的值可能为( ).
A. ﹣12 B. ﹣8 C. ﹣2 D. 0
【答案】BCD
【解析】
【分析】先由正弦定理求出 ,进而得到 ⊥ ,建立平面直角坐标系,设 , ,表
达出 ,求出 的取值范围,得到答案.
【详解】因为 ,
所以由正弦定理得, ,
又 ,故 ,
又 , ,故 ⊥ ,
第8页/共21页
学科网(北京)股份有限公司以 为坐标原点, 所在直线分别为 轴,建立空间直角坐标系,
则 ,设 , ,
则 ,
则 ,
因为 ,所以 ,
A错误,BCD正确.
故选:BCD
12. 已知函数 ,则下列结论正确的是( )
A. 是周期为 的奇函数 B. 在 上为增函数
C. 在 内有20个极值点 D. 在 上恒成立的充要条件是
【答案】BCD
【解析】
【分析】A选项,根据函数奇偶性定义得到函数为奇函数,但 ,A错误;B选项,求导
得到函数单调性;C选项,求导,令导函数等于0,检验后得到极值点个数;D选项,求导后,分 与
两种情况,结合放缩法得到结论.
第9页/共21页
学科网(北京)股份有限公司【详解】A选项, 的定义域为R, , 是奇函数,
但是 , 不是周期为 的函数,故A错误;
B选项,当 时, , , 单调递增,
当 时, , , 单调递增,
且 在 连续,故 在 单调递增,故B正确;
C选项,当 时, , ,
令 得, ,
当 时, , ,
令 得, ,且以上零点均为变号零点,
故均为极值点,因此, 在 内有20个极值点,故C正确;
D选项,由题意得 在 上恒成立,令 ,
当 时, ,令 , ,
,因为 ,所以 ,
则 ,由于 ,故 ,
当且仅当 时,等号成立,故 在 上单调递增,
第10页/共21页
学科网(北京)股份有限公司所以 ,故满足 在 上恒成立;
当 时, ,
由于 ,所以 ,则 ,
又 ,故 ,
若 ,此时 ,
则 在 单调递减,则 ,不合要求,
若 ,则存在 ,使得 ,
当 时, ,当 时, ,
故 在 处取得极小值,且 ,不合要求.
综上: ,故D正确;
故选:BCD.
【点睛】方法点睛:对于求不等式成立时的参数范围问题,一般有三个方法:一是分离参数法,使不等式
一端是含有参数的式子,另一端是一个区间上具体的函数,通过对具体函数的研究确定含参式子满足的条
件.二是讨论分析法,根据参数取值情况分类讨论.三是数形结合法,将不等式转化为两个函数,通过两个
函数图像确定条件.
第Ⅱ卷 非选择题(共90分)
三、填空题:(本大题共4小题,每小题5分,共20分.把答案填在答题纸上.)
13. 已知单位向量 满足 若向量 则 _____.
【答案】 ##0.5
第11页/共21页
学科网(北京)股份有限公司【解析】
【分析】根据已知条件结合数量积的运算公式可求出 和 的值,从而根据向量夹角的计算公式即可求
出 的值.
【详解】因为 为单位向量, 所以 ,
又因为 所以 ,
,
又因为 ,所以 .
故答案为: .
14. 在等差数列 中, 为其前n项和.若 ,则数列 的公差d=______.
【答案】2
【解析】
【分析】由等差数列的性质得 为等差数列后求解.
【详解】由题意得 ,故 ,
故 是以 为首项, 为公差的等差数列, ,得 ,
故答案为:2
15. 在平面直角坐标系中,已知点 为角 终边上一点,若 , ,则
______.
第12页/共21页
学科网(北京)股份有限公司【答案】
【解析】
【分析】根据三角函数的定义求出 与 ,再结合 及 求出 ,最后利
用余弦差角公式求出答案.
【详解】因为点 为角 终边上一点, , , ,
,
因为 ,所以 , ,
因为 ,所以 , ,
故 ,
所以
.
故答案为: .
16. 数列 满足 则数列 的前60项和为______.
【答案】
【解析】
【分析】先由已知递推式得到 , ,再对数列分组求和,即可解答.
第13页/共21页
学科网(北京)股份有限公司【详解】由 , 得
,
,
所以 ,
即 ,又 ,所以 ,
所以数列 为各项均为1的常数数列,
所以 ,
又由 得
,
,
即 ,
所以
,
第14页/共21页
学科网(北京)股份有限公司所以数列 的前60项和为 .
故答案为: .
四、解答题:(满分70分.解答应写出文字说明,证明过程或演算步骤,解答过程书写在答
题纸的对应位置.)
17. 已知函数 的最大值为1.
(1)求a的值;
(2)将 的图象向上平移1个单位,再把图象上所有点的纵坐标缩短到原来的 (横坐标不变),再
把图象上所有点的横坐标缩短到原来的 (纵坐标不变),得到函数 的图象,在 中,角A,
B,C的对边分别为a,b,c,若 求 面积的最大值.
【答案】(1)
(2)
【解析】
【分析】(1)先应用两角和差公式结合辅助角公式化简,再应用三角函数最值求参即可;
(2)先由 求出 ,再应用余弦定理结合不等式求面积的最值.
【小问1详解】
∵函数
,
函数的最大值为 ,
∴ , .
第15页/共21页
学科网(北京)股份有限公司【小问2详解】
由已知 则
因为在 中, ,所以
所以 ,所以
又由余弦定理及 得: ,
即 ,
所以 ,即 (当且仅当 时等号成立).
所以 .
18. 已知等差数列 的公差 ,其前n项和为 ,若 ,且 , , 成等比数列.
(1)求数列 的通项公式;
(2)若 ,求 的取值范围.
【答案】(1)
(2)
【解析】
【分析】(1)根据等差数列和等比数列的基本量运算求出等差数列的首项和公差,写出通项公式即可;
(2)利用等差数列前n项和公式求出 ,然后利用裂项相消法求得 ,利用 单调性即可求得范围.
【小问1详解】
第16页/共21页
学科网(北京)股份有限公司因为 为等差数列,且 ,
所以 ,由 成等比数列,得 ,
即 ,
因为 ,所以 ,所以 ,
故 ;
【小问2详解】
因为 ,所以 ,
所以
,故 .
因为 ,即 是递增数列,所以 ,
所以
19. 设函数 .
(1)若 ,求 在 处的切线方程;
(2)当 时,证明: .
【答案】(1)
(2)证明见解析
【解析】
第17页/共21页
学科网(北京)股份有限公司【分析】(1)利用导数几何意义求切线方程;
(2)通过构造新函数求最值即可证明.
【小问1详解】
时,
所以 ,
所以 在 处的切线方程为 .
【小问2详解】
证明:当 时, 化为 .
令 ,
时, ,此时函数 单调递减;
,此时函数 单调递增.
时,函数 取得极小值即最小值,
所以只要证明 ,
即证明 即可.
令 , ,
,
可得 时,函数 取得极小值即最小值, ,
第18页/共21页
学科网(北京)股份有限公司所以 在 上恒成立,
所以,当 时, 成立.
【点睛】利用导数证明不等式 的方法主要有:①构造函数 ,求解函数的最小
值大于零;②分别求解 的最小值和 的最大值可证结论;③利用常见不等式进行放缩证明.
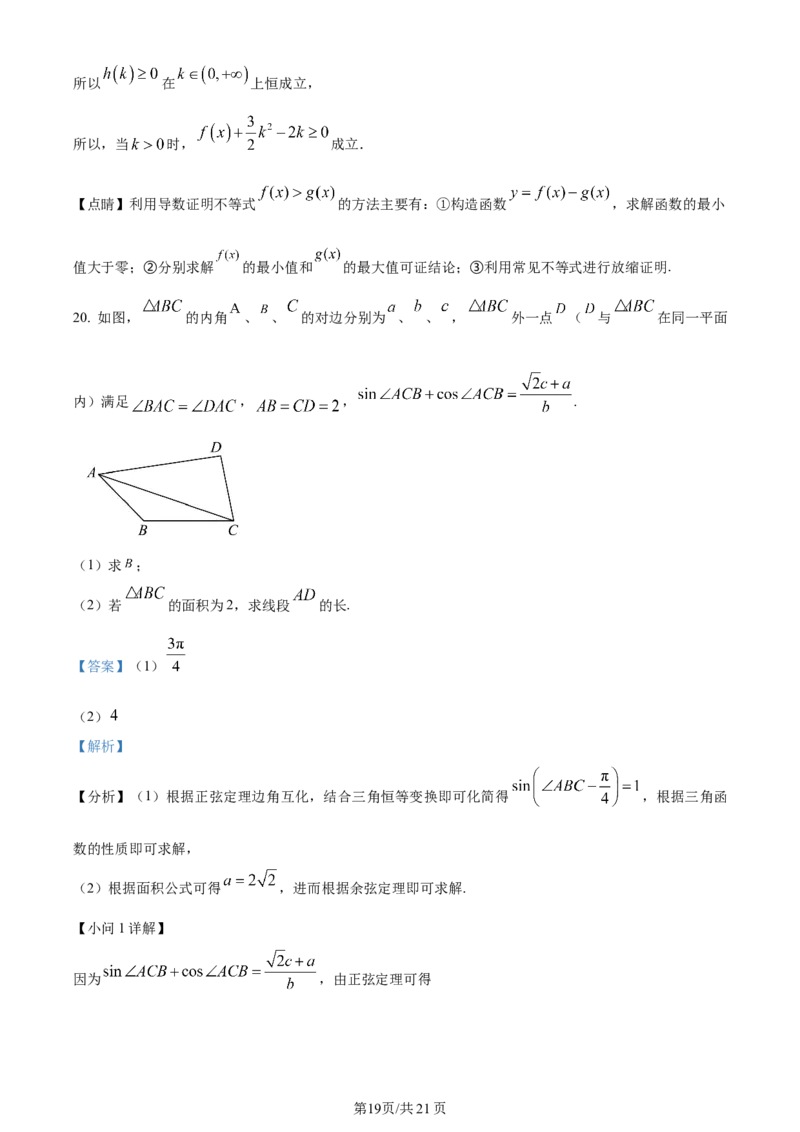
20. 如图, 的内角 、 、 的对边分别为 、 、 , 外一点 ( 与 在同一平面
内)满足 , , .
(1)求 ;
(2)若 的面积为2,求线段 的长.
【答案】(1)
(2)
【解析】
【分析】(1)根据正弦定理边角互化,结合三角恒等变换即可化简得 ,根据三角函
数的性质即可求解,
(2)根据面积公式可得 ,进而根据余弦定理即可求解.
【小问1详解】
因为 ,由正弦定理可得
第19页/共21页
学科网(北京)股份有限公司,
即
,
即 .
又 , ,故 ,即 ,
所以 ,即 ,
因为 , ,所以 ,得 .
【小问2详解】
因为 的面积 ,所以 ,
即 , ,
由余弦定理得 ,
所以 ,
因为 平分 ,所以 ,所以 .
第20页/共21页
学科网(北京)股份有限公司21. 已知数列 中 ,其前 项和为 ,且对任意 ,都有 .等比数列 中,
, .
(1)求数列 、 的通项公式;
(2)求数列 的前 项和 .
【答案】(1) ;(2)
【解析】
【详解】试题分析:(1)由已知条件可得 ,根据 可得数列 是
等差数列,故可得其通项公式,根据等比数列的性质可求出公比 继而可求出 的通项公式;(2)根
据等比数列前 项和公式可得 前 项和 ,分为 为奇数和 为偶数,利用并项求和可求得 的
前 项和 ,进而可得结果.
试题解析:(1)由 得 ,……………①
当 时, ,………………②
由①-②得, ,
即 ,整理得 ,
∵ ,∴ ,
由已知得,当 时, ,即 ,解得 .
第21页/共21页
学科网(北京)股份有限公司故数列 是首项为1,公差为2的等差数列.
∴ .
设等比数列 的公比为 ,则 ,所以 .
故 ,即 ,解得 .
故 .
(2)记数列 的前 项和为 ,数列 的前 项和为 .
则 .
当 为偶数时,奇数项与偶数项各有 项.
则
;
当 为奇数时,奇数项为 项,偶数项为 项.
则
.
所以 .
点睛:本题主要考查了等差数列,等比数列的概念,以及数列的求和,属于高考中常考知识点,难度不大;
第22页/共21页
学科网(北京)股份有限公司常见的数列求和的方法有公式法即等差等比数列求和公式,分组求和类似于 ,其中 和
分别为特殊数列,裂项相消法类似于 ,错位相减法类似于 ,其中 为等
差数列, 为等比数列等.
22. 已知函数 .
(1)当 时,求函数 的极小值;
(2)若 上,使得 成立,求 的取值范围.
【答案】(1)2;(2) .
【解析】
【详解】试题分析:(1)将参数值代入表达式,再进行求导,根据导函数的正负得到原函数的单调性,
进而得到极值;(2) ,有解,即h(x)的最小值小于0即可,对函数求导,研究
函数的单调性,得到最小值即可.
解析:
(1)当 时,
令 0,得
且 在 上单调递增,在 上单调递减,在 上单调递增
所以 在 时取得极小值为 .
第23页/共21页
学科网(北京)股份有限公司(2)由已知: ,使得
,即:
设 ,则只需要函数 在 上的最小值小于零.
又 ,
令 ,得 (舍去)或 .
①当 ,即 时, 在 上单调递减,
故 在 上的最小值为 ,由 ,可得 .
因为 ,所以 .
②当 ,即 时, 在 上单调递增,
故 在 上的最小值为 ,由 ,
可得 (满足 ).
③当 ,即 时, 在 上单调递减,在 上单
调递增,故 在 上的最小值为 .
因为 ,所以 ,
所以 ,即 ,不满足题意,舍去.
综上可得 或 ,
第24页/共21页
学科网(北京)股份有限公司所以实数 的取值范围为 .
点睛:导数问题经常会遇见恒成立的问题:
(1)根据参变分离,转化为不含参数的函数的最值问题;
(2)若 就可讨论参数不同取值下的函数的单调性和极值以及最值,最终转化为 ,
若 恒成立 ;
(3)若 恒成立,可转化为 (需在同一处取得最值)
第25页/共21页
学科网(北京)股份有限公司