陕西金科联考高三上（开学考）-数学试题+答案(1)_2023年9月_029月合集_2024届山西省金科大联考高三上学期开学检测

2023-2024 学年高三上学期开学质量检测 数学试题 考生注意： 1．本试卷分选择题和非选择题两部分。满分150分，考试时间120分钟。 2．答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。 3．考生作答时，请将答案答在答题卡上。选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答 案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书 ．．．．．．． 写的答案无效，在试题卷、草稿纸上作答无效。 ．．．．．． ．．．． ．．．．．．．． 4．本卷命题范围：高考范围。 一、选择题：本题共 8小题，每小题 5分，共 40分．在每小题给出的四个选项中，只有一项是 符合题目要求的． 1．若复数z满足(1+i)z =3−i，则|z|=（ ） A． 5 B．5 C．2 5 D．20 2．已知全集U =R，集合A={x|x2 −2x−30}，B ={x| y =lg(2−x)}，则ð (A B)=（ ） U A．(−,−1] (2,+) B．(−,−1) [2,+) C．(3,+) D．[3,+) 5 3．一组数据按从小到大的顺序排列为1，3，5，6，m，10，12，13，若该组数据的中位数是极差的 ，则该 8 组数据的第60百分位数是（ ） A．7.5 B．8 C．9 D．9.5 1 4．设向量a ，b 的夹角的余弦值为− ，|a|=4，|b |=1，则(2a+3b)b =（ ） 4 A．−1 B．1 C．−5 D．5 9 5．已知sin(5+)=5sin( +)，则sin2+sin2=（ ） 2 9 11 15 20 A．− B． C． D． 26 26 26 13 6．在平面直角坐标系xOy中，扡物线C: y2 =16x的焦点为F，P是C上的一点，点M是y轴上的一点，且 MF =2PF ．则△OMF的面积为（ ） A．24 3 B．16 3 C．24 2 D．16 2 7．暑假期间，同学们参加了几何模型的制作比赛，大家的作品在展览中获得了一致好评．其中甲的作品是在 球当中放置了一个圆锥，于是就产生了这样一个有趣的问题：已知圆锥的顶点和底面圆周都在球O的球面上， 学科网（北京）股份有限公司2 若圆锥的侧面展开图的圆心角为 ，面积为12，则球O的表面积为（ ） 3 81 81 121 121 A． B． C． D． 8 2 16 4 8．已知函数 f(x)=2cos(x+)(0,0)的最小正周期为T，若 f(T)= 3，且 f(x)在区间[0,1] 上恰有3个零点，则的取值范围是（ ） 17 23 17 23 7 10 7 10 A．( , ] B．[ , ) C．( , ] D．[ , ) 6 6 6 6 3 3 3 3 二、选择题：本大题共 4小题，每小题 5分，共 20分。在每小题给出的选项中，有多项符合题 目要求。全部选对的得 5分，有选错的得 0分，部分选对的得 2分。 9．下列说法正确的的是（ ） a b A．若a b．则ac2 bc2 B．若  ，则a b c2 c2 a+c a C．若a b，c d ．则ac bd D．若ba 0，c 0，则  b+c b 10．甲箱中有 4 个红球、4 个黄球，乙箱中有 6 个红球、2 个黄球（这 16 个球除颜色外，大小、形状完全相 同），先从甲箱中随机取出1个球放入乙箱，再从乙箱中随机取出1个球，记“在甲箱中取出的球是红球”为 事件A ，“在甲箱中取出的球是黄球”为事件A ，“从乙箱中取出的球是黄球”为事件B．则下列说法正确的 1 2 是（ ） 2 A．A 与A 是互斥事件 B．P(A,B)= 1 2 9 5 C．P(B)= D．A 与B相互独立 18 2 11．已知正方体ABCD−ABC D 的棱长为4，点E，F，G，M分别是BC，AA ，C D ，BB 的中点．则 1 1 1 1 1 1 1 1 下列说法证确的是（ ） A．直线GF ，EC 是异面直线 1 B．直线EG与平面ABCD所成角的正切值为2 2 C．平面DMC 截正方体所得截面的面积为18 1 16 D．三棱锥D −AMC 的体积为 1 1 3 12．已加点P是圆O:x2 + y2 =9上的一点．直线l :xcos+ ysin=3与直线l :xsin− ycos=2交于 1 2 点M．则下列说法正确的是（ ） A．l ⊥l B．直线l 与圆O相切 1 2 1 C．直线l 被圆O截得的弦长为 5 D．|PM |的最小值为 13−3 2 学科网（北京）股份有限公司三、填空题：本题共 4小题，每小题 5分，共 20分． 1 13．(3x3− )6的展开式中，x2项的系数为________． x log x, x 0  3 14．已知函数 f(x)=  1 ，若 f(f(x))=1，则x的值为________． ( )x−1, x0   3 x2 y2 15．已知椭圆C + =1(a b0)的左、右焦点分别为F ，F ，点P，Q为C上关于坐标原点对称的 1 a2 b2 1 2 4 两点，且|PQ|=|FF |，且四边形PFQF 的面积为 a2，则C的离心率为________． 1 2 1 2 9 16．已知函数 f(x)=ex −e−x −2sinx，不等式 f(a−x2ex)+ f(2lnx+x)0对任意的x(0,+)恒成立， 则a的最大值为________． 四、解答题：本题共 6小题，共 70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分） 设S 为公差不为0的等差数列{a }的前n项和，若a ，a ，a 成等比数列，S =144． n n 2 5 14 12 （1）求{a }的通项公式； n 4n2 （2）设b = ，求数列{b }的前n项和T ． n a a n n n n+1 18．（本小题满分12分） 电影评论，简称影评，是对一部电影的导演、演员、镜头、摄影、剧情、线索、环境、色彩、光线、视听 语言、道具作用、转场、剪辑等进行分析和评论．电影评论的目的在于分析、鉴定和评价蕴含在银幕中的审美 价值、认识价值、社会意义、镜头语言等方面，达到拍摄影片的目的，解释影片中所表达的主题，既能通过分 析影片的成败得失，帮助导演开阔视野，提高创作水平，以促进电影艺术的繁荣和发展；同时能通过分析和评 价，影响观众对影片的理解和鉴赏，提高观众的欣赏水平，从而间接促进电影艺术的发展．某观影平台为了解 观众对最近上映的某部影片的评价情况（评价结果仅有“好评”“差评”），从平台所有参与评价的观众中随机 抽取220人进行调查，得到数据如下表所示（单位：人）： 好评 差评 合计 男性 70 110 女性 60 合计 220 （1）请将22列联表补充完整，并依据小概率值=0.010的独立性检验，能否认为对该部影片的评价与性 别有关联？ （2）从给出“好评”的观众中按性别用分层抽样的方法抽取10人，再从这10人中随机抽出3人送电影优惠 券，记随机变量X表示这3人中女性观众的人数，求X的分布列和数学期望． 学科网（北京）股份有限公司n(ad −bc)2 参考公式：2 = ，其中n=a+b+c+d ． (a+b)(c+d)(a+c)(b+d)  0.10 0.05 0.010 0.005 0.001 参考数据： x 2.706 3.841 6.635 7.879 10.828 19．（本小题满分12分） c b−a a 在△ABC 中，内角A，B，C的对边分别为a，b，c，且 = + ． sinA+sinB sinC sinA+sinB （1）求角B的大小； （2）若AC =2 7 ，D是边AC 的中点，且BD = 19 ，求△ABC 的内切圆的半径． （1）当a =6时，求图中阴影部分表示的集合C； （2）在①(ð A) B =；②A B = B；③A B = A这三个条件中任选一个作为已知条件，求实数 a的 R 取值范围． 20．（本小题满分12分） 如图，在四棱锥P− ABCD中，PB ⊥平面ABCD，AD BC ，AB ⊥ BC ，AB = AD =1，BC =2，点 E是棱PD上的一点． （1）若BE ⊥ PD，求证：平面EBC ⊥平面PCD； （2）若PB =1，DE =2PE，求平面EBC 与平面PAD的夹角的余弦值． 21．（本小题满分12分） x2 y2 6 已知双曲线C: − =1(a 0,b0)的离心率为 ，且过点P(2,1)． a2 b2 2 （1）求C的方程； （2）设A，B为C上异于点P的两点，记直线PA，PB的斜率分别为k ，k ，若(2k −1)(2k −1)=1，试 1 2 1 2 判断直线AB是否过定点？若是，则求出该定点坐标；若不是，请说明理由． 22．（本小题满分12分） 2a 已知函数 f(x)=ax−lnx− (aR)． x （1）讨论 f(x)的单调性； 2−16a2 （2）若 f(x)的两个极值点分别为x ，x ，证明：| f(x )− f(x )| ． 1 2 1 2 2a 学科网（北京）股份有限公司2023～2024 学年高三上学期开学质量检测·数学试题 参考答案、提示及评分细则 3−i (3−i)(1−i) 1．A 因为(1+i)z =3−i，所以z = = =1−2i，所以|z|= 12 +(−2)2 = 5．故选A． 1+i (1+i)(1−i) 2．C 由题意知A={x|x2 −2x−30}=[−1,3]，B ={x| y =lg(2−x)}=(−,2)，所以A B = (−,3]， 所以ð (A B)=(3,+)．故选C． U 6+m 6+m 5 3．C 由题意知，中位数是 ，极差为13−1=12，所以 =12 ，解得m=9，又860% =4.8， 2 2 8 则第60百分位数是9．故选C． 1 1 4．B 设a 与b 的夹角为，因为a 与b 的夹角的余弦值为− ，即cos=− ，又|a|=4，|b |=1，所以 4 4 1 ab =|a||b |cos=14(− )=−1，所以(2a+3b)b =2ab +3b2 =−2+3=1．故选B． 4 9 5．C 由sin(5+)=5sin( +) ，可得 −sin=5cos，即 tan=−5 ，所以sin2+sin2= 2 sin2+sin2 2sincos+sin2 2tan+tan2 2(−5)+(−5)2 15 = = = = ．故选C． sin2+cos2 sin2+cos2 1+tan2 1+(−5)2 26 6．D 由题意知F(4,0)，设M(0,m)，P(x ,y )，所以MF =(4,−m)，PF =(4−x ,−y )，又MF =2PF ， 0 0 0 0 m m 所以(4,−m)=2(4−x ,−y )，所以x =2，y = ，所以( )2 =162，解得m=8 2 ，所以△OMF 0 0 0 0 2 2 1 的面积S = |OF ||m|=16 2 ．故选D． 2 2 7．B 圆锥的顶点和底面圆周都在球O 的球面上，圆锥的侧面展开图的圆心角为 ，面积为12，设圆锥 3 1 2 2 的母线长为l，所以  l2 =12，解得l =6．设圆锥的底面圆半径为r，所以2r = l =4，解得 2 3 3 9 r =2，所以圆锥的高h= 62 −22 =4 2 ，设球O的半径为R，所以r2 +(4 2 −R)2 = R2，解得R = ， 2 2 81 81 所以球O的表面积等于4R2 =4 = ．故选B． 8 2 2 8．D 由题意 f(x)=2cos(x+)(0,0)的最小正周期为T，则T = ，又 f(T)= 3，可得  学科网（北京）股份有限公司2 3 3   cos( +)= ，即cos= ，又0，所以= ，由 f(x)=2cos(x+ )在区间[0,1]  2 2 6 6    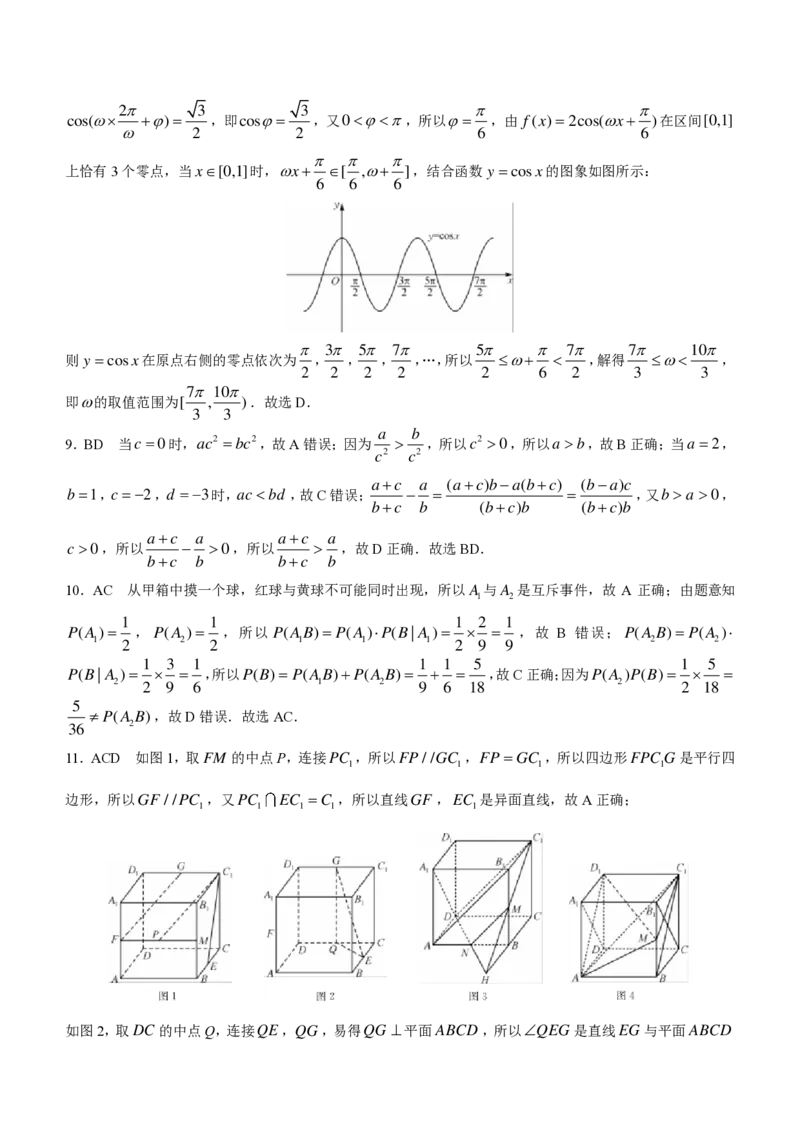上恰有3个零点，当x[0,1]时，x+ [ ,+ ]，结合函数y =cosx的图象如图所示： 6 6 6  3 5 7 5  7 7 10 则 y =cosx在原点右侧的零点依次为 ， ， ， ，…，所以 +  ，解得  ， 2 2 2 2 2 6 2 3 3 7 10 即的取值范围为[ , )．故选D． 3 3 a b 9．BD 当c =0时，ac2 =bc2，故A错误；因为  ，所以c2 0，所以a b，故B正确；当a =2， c2 c2 a+c a (a+c)b−a(b+c) (b−a)c b=1，c =−2，d =−3时，ac bd ，故C错误； − = = ，又b  a 0， b+c b (b+c)b (b+c)b a+c a a+c a c 0，所以 − 0，所以  ，故D正确．故选BD． b+c b b+c b 10．AC 从甲箱中摸一个球，红球与黄球不可能同时出现，所以A 与A 是互斥事件，故 A 正确；由题意知 1 2 1 1 1 2 1 P(A)= ， P(A )= ，所以 P(AB)= P(A)P(B| A)=  = ，故 B 错误； P(A B)= P(A ) 1 2 2 2 1 1 1 2 9 9 2 2 1 3 1 1 1 5 1 5 P(B| A )=  = ，所以P(B)= P(AB)+P(A B)= + = ，故C正确；因为P(A )P(B)=  = 2 2 9 6 1 2 9 6 18 2 2 18 5  P(A B)，故D错误．故选AC． 36 2 11．ACD 如图1，取FM 的中点P，连接PC ，所以FP//GC ，FP =GC ，所以四边形FPCG是平行四 1 1 1 1 边形，所以GF //PC ，又PC EC =C ，所以直线GF ，EC 是异面直线，故A正确； 1 1 1 1 1 如图2，取DC 的中点Q，连接QE，QG，易得QG ⊥平面ABCD，所以QEG是直线EG 与平面ABCD 学科网（北京）股份有限公司QG 所成角，易得QE =2 2，QG =4，所以tanQEG = = 2 ，即直线EG与平面ABCD 所成角的正切 QE 值为 2 ，故B错误； 如图 3，延长C M ，CB交于点 H，连接HD交AB于点 N，连接MN ，AB ，因为BB //CC ，M 为BB 1 1 1 1 1 1 的中点，则BM = CC ，所以B为HC 的中点，因为AB//CD，所以N为AB的中点，则MN //AB ，因 2 1 1 为AD//BC ，AD = BC ，所以四边形ABC D为平行四边形，所以AB //DC ，所以MN //DC ，则平 1 1 1 1 1 1 1 1 1 面DMC 截正方体所得截面为等腰梯形MNDC ，在等腰梯形MNDC 中，DC =4 2 ，MN =2 2 ，DN = 1 1 1 1 (4 2+2 2)3 2 MC =2 5，则梯形的高为 20−2 =3 2，所以等腰梯形MNDC 的面积为 =18，故 1 1 2 C正确； 如图4，连接BC ，BC，则BC ⊥ BC，因为AB ⊥平面BCC B ，BC 平面BCC B ，所以AB ⊥ BC ， 1 1 1 1 1 1 1 1 1 1 又AB BC = B，AB，BC 平面ABC D ，所以BC ⊥平面ABC D ，又M为BB 的中点，所以三棱 1 1 1 1 1 1 1 1 1 1 1 锥M −AC D 的高为 BC = 2 ，S = 4 24=8 2，所以V =V = 8 2 2 = 1 1 4 1 △AC 1 D 1 2 D 1 −AMC 1 M−AC 1 D 1 3 16 ，故D正确．故选ACD． 3 12．ABD 因为cossin+sin(−cos)=0 ，所以l ⊥l ，故 A 正确；圆心 O 到l 的距离为d = 1 2 1 3 2 =3，所以l 与圆O相切，故B正确；圆心O到直线l 的距离为d= =2， 1 2 cos2+sin2 sin2+(−cos)2 xcos+ ysin=3 x =3cos+2sin 所以弦长为 2 32 −22 =2 5 ，故 C 错误；由  ，得  ，即 xsin− ycos=2 y =3sin−2cos M(3cos+2sin,3sin−2cos)，所以|OM |= (3cos+2sin)2 +(3sin−2cos)2 = 13 ，所以 |PM |的最小值为 13−3，故D正确．故选ABD． 1 13．135 展开式的通项公式T =Cr(3x3)6−r(− )r =(−1)r36−rCr x18−4r，令18−4r =2，解得r =4， r+1 6 x 6 所以x2项的系数为(−1)436−4C4 =915=135． 6 14．0或27 令 f(x)=t，即 f(t)=1．当t 0时，f(t)=log t =1，解得t =3，即 f(x)=3，当x 0时， 3 1 f(x)=log x =3，解得x =27，符合题意；当x0时，f(x)=( )x−1 =3，解得x =0，符合题意；当t 0 3 3 学科网（北京）股份有限公司1 时， f(t)=( )t−1 =1，解得t =1，不符合题意．综上，x的值为0或27． 3 7 15． 由已知及对称性得：四边形PFQF 为矩形，即PF ⊥ PF ，所以S =2S =|PF ||PF |， 3 1 2 1 2 PF 1 QF 2 △PF 1 F 2 1 2 |PF |+|PF |=2a 4 由椭圆定义与勾股定理知： 1 2 ，所以|PF ||PF |=2b2，所以 a2 =2b2 = 2(a2 −c2)， |PF |2 +|PF |2=4c2 1 2 9 1 2 c 7 7 所以 = ，即C的离心率为 ． a 3 3 16．1 因为 f(−x)=e−x −e−(−x) −2sin(−x)=e−x −ex +2sinx =−f(x)，所以 f(x)为R 上的奇函数．又 f(x)=ex +e−x −2cosx2 exe−x −2cosx =2−2cosx0，所以 f(x)在(−,+)上单调递增．不等式 f(a−x2ex)+ f(2lnx+x)0 对任意的 x(0,+) 恒成立，即 f(2lnx+x) f(x2ex −a) 对任意的 x(0,+) 恒 成 立 ， 所 以 2lnx+x x2ex −a 对 任 意 的 x(0,+) 恒 成 立 ， 即 a  x2ex − (2lnx+x)=elnx2 ex −(2lnx+x)=e2lnx+x −(2lnx+x)对任意的x(0,+)恒成立．令h(x)=ex −x，所 以h(x)=ex −1，所以当x 0时，h(x)0，h(x)在(0,+)上单层0时，h(x)0，h(x)在(−,0)上 单调递减．所以h(x) =h(0)=e0 −0=1，所以[e2lnx+x −(2lnx+x)] =1，此时2lnx+x =0，所以a 1， min min 即a的最大值为1． 17．解：（1）设等差数列{a }的公差为d ，d 0， n 因为a ，a ，a 成等比数列，所以a2 =a a ，所以(a +4d)2 =(a +d)(a +13d)， 2 5 14 5 2 14 1 1 1 d 所以2a d −d2 =0，又d 0，所以2a −d =0，所以a = ， 1 1 1 2 1211d d 所以S =12a + =12 +66d =72d =144， 12 1 2 2 解得d =2，所以a =1， 1 所以{a }的通项公式a =1+2(n−1)=2n−1． n n 4n2 4n2 1 1 1 1 （2）由（1）知b = = =1+ =1+ ( − )， n a a (2n−1)(2n+1) (2n−1)(2n+1) 2 2n−1 2n+1 n n+1 学科网（北京）股份有限公司1 1 1 1 1 1 1 1 所以T =b +b + +b =1+ (1− )+1+ ( − )+ +1+ ( − ) n 1 2 n 2 3 2 3 5 2 2n−1 2n+1 1 1 n =n+ (1− )=n+ . 2 2n+1 2n+1 18．解：（1）22列联表如下： 好评 差评 合计 男性 40 70 110 女性 60 50 110 合计 100 120 220 零假设为H ：对该部影片的评价与性别无关联． 0 根据列联表中的数据，经计算得到 n(ad −bc)2 220(4050−7060)2 22 2 = = = 7.3336.635= x ， (a+b)(c+d)(a+c)(b+d) 100120110110 3 0.010 根据小概率值=0.010的独立性检验，我们推断H 不成立，即认为对该部影片的评价与性别有关联，此推 0 断犯错误的概率不大于0.010． （2）从给出“好评”的观众中按性别用分层抽样的方法抽取10人， 40 60 男性有：10 =4（人），女性有：10 =6（人）． 40+60 40+60 X的所有可能取值为0，1，2，3， C3 1 C2C1 3 C1C2 1 C3 1 所以P(X =0)= 4 = ，P(X =1)= 4 6 = ，P(X =2)= 4 6 = ，P(X =3)= 6 = ， C3 30 C3 10 C3 2 C3 6 10 10 10 10 所以X的分布列为 X 0 1 2 3 1 3 1 1 P 30 10 2 6 1 3 1 1 9 所以E(X)=0 +1 +2 +3 = ． 30 10 2 6 5 c b−a a 19．解：（1）因为 = + ， sinA+sinB sinC sinA+sinB c b−a a 由正弦定理得 = + ，所以a2 +c2 −b2 =ac， a+b c a+b a2 +c2 −b2 ac 1 由余弦定理得cosB= = = ， 2ac 2ac 2  又B(0,)，所以B = ． 3 学科网（北京）股份有限公司（2）由余弦定理得AC2 = BA2 +BC2 −2BABCcosABC ，即28=a2 +c2 −ac． 1 又D是边AC 的中点，且BD = 19 ，所以BD = (BA+BC)， 2 2 1 1 2 2 1 所以BD = (BA+BC)2 = (BA +2BABC+BC )，即19= (c2 +ac+a2)， 4 4 4 所以a2 +c2 =52，ac =24，所以a+c = a2 +c2 +2ac =10． 1 1 设△ABC 的内切圆的半径为r，所以 (AB+AC+BC)r = BABCsinABC， 2 2 3 24 BABCsinABC 5 3− 21 2 所以r = = = ． AB+AC+BC 10+2 7 3 20．（1）证明：连接BD，取BC中点F，连接DF，如图所示． 因为AD =1，BC =2，所以AD//BF ，AD = BF ，所以四边形ABFD为平行四边形． 所以AB = DF =1，则DF =CF = BF =1，所以CDB =90，即CD ⊥ BD． 因为PB ⊥平面ABCD，CD平面ABCD，所以PB ⊥CD ， BD BP = B，BD，BP平面PBD，所以CD ⊥平面PBD， 又BE 平面PBD，所以CD ⊥ BE ． 又BE ⊥ PD，PD CD = D，PD，CD平面PCD，所以BE ⊥平面PCD， 又BE 平面EBC ，所以平面EBC ⊥平面PCD． （2）解：以B 为坐标原点，BC，BA，BP所在的直线分别为x轴，y轴，z轴，建立空间直角坐标系，如 图所示．所以B(0,0,0)，C(2,0,0)，D(1,1,0)，A(0,1,0)，P(0,0,1)，所以AD =(1,0,0)，DF =(−1,−1,1)，  ADn = x =0 设平面PAD的一个法向量n =(x ,y ,z )，所以 1 1 ．令y =1，解得x =0，z =1， 1 1 1 1 1 1 1  DPn =−x − y +z =0 1 1 1 1 所以平面PAD的一个法向量n =(0,1,1)． 1 2 2 2 2 因为DE =2PE，所以DE = DP =(− ,− , )， 3 3 3 3 2 2 2 1 1 2 所以BE = BD+DE =(1,1,0)+(− ,− , )=( , , )，BC =(2,0,0)， 3 3 3 3 3 3 设平面EBC 的一个法向量n =(x ,y ,z )， 2 2 2 2  1 1 2 BEn = x + y + z =0 所以 2 3 2 3 2 3 2 令z =1，解得x =0， y =−2， 2 2 2  BCn =2x =0  2 2 所以平面EBC 的一个法向量n =(0,−2,1)． 2 学科网（北京）股份有限公司设平面EBC 与平面PAD的夹角为， |n n | 1 10 所以cos=|cosn ,n |= 1 2 = = ． 1 2 |n ||n | 1+1 4+1 10 1 2 10 即平面EBC 与平面PAD的夹角的余弦值为 ． 10 c 6  = a 2  21．（1）解：由题意知 4 1 ， − =1  a2 b2  c2 =a2 +b2 解得a = 2，b=1，c = 3， x2 所以C的方程为 − y2 =1． 2 （2）证明：设A(x ,y )，B(x ,y )． 1 1 2 2 y −1 y −1 又P(2,1)，则k = 1 ，k = 2 ． 1 x −2 2 x −2 1 2 y −1 y −1 y −1 y −1 因为(2k −1)(2k −1)=1，所以k +k =2k k ，所以 1 + 2 =2 1  2 ， 1 2 1 2 1 2 x −2 x −2 x −2 x −2 1 2 1 2 (y −1)(x −2) (y −1)(x −2) y −1 y −1 即 1 2 + 2 1 =2 1  2 ， (x −2)(x −2) (x −2)(x −2) x −2 x −2 1 2 1 2 1 2 所以(y −1)(x −2)+(y −1)(x −2)=2(y −1)(y −1)， 1 2 2 1 1 2 所以y x + y x −x −x +2=2y y ， 1 2 2 1 2 1 1 2 当直线AB的斜率为0时，x =−x ，y = y ，所以y2 =1，解得y =1或 y =−1，不符合题意，所以直线 2 1 2 1 1 1 1 AB的斜率不为0． 设直线AB的方程为x =my+n， x =my+n  由x2 得(m2 −2)y2 +2mny+n2 −2=0， − y2 =1   2  =4m2n2 −4(m2 −2)(n2 −2)=8(m2 +n2 −2)0，即m2 +n2 2， 学科网（北京）股份有限公司−2mn n2 −2 所以y + y = ， y y = ． 1 2 m2 −2 1 2 m2 −2 所以y (my +n)+ y (my +n)−(my +n)−(my +n)+2=2y y ， 1 2 2 1 2 1 1 2 整理得(2m−2)y y +(n−m)(y + y )−2n+2=0， 1 2 1 2 (2m−2)(n2 −2) −2mn(n−m) (−2n+2)(m2 −2) 所以 + + =0， m2 −2 m2 −2 m2 −2 所以(2m−2)(n2 −2)−2mn(n−m)+(−2n+2)(m2 −2)=0， 整理得m2 −n2 −2m+2n=0， 即(m−n)(m+n−2)=0，则m=n或m=2−n． 当m=n时，直线AB的方程为x =ny+n=n(y+1)，此时直线AB过定点(0,−1)； 当m=2−n时，直线AB的方程为x =(2−n)y+n=n(1− y)+2y，此时直线AB过定点(2,1)． 即为P(2,1)，因为A，B为C上异于点P(2,1)的两个动点，所以不符合题意． 故直线AB过的定点为(0,−1)． 1 2a ax2 −x+2a 22．（1）解：依题意， f(x)=a− + = (x 0)， x x2 x2 当a 0时， f(x)0，所以 f(x)在(0,+)上单调递减； 2 1− 1−8a2 1+ 1−8a2 当0a 时，令 f(x)0，解得0 x 或x  ，令 f(x)0，解得 4 2a 2a 1− 1−8a2 1+ 1−8a2 1− 1−8a2 1− 1−8a2 1+ 1−8a2  x ，所以 f(x)在(0, )上单调递增，在( , ) 2a 2a 2a 2a 2a 1+ 1−8a2 上单调递减，在( ,+)上单调递增； 2a 2 当a  时， f(x)0，所以 f(x)在(0,+)上单调递增． 4 2 （2）证明：不妨设0 x  x ，由（1）知，当0a 时， f(x)在(0,x )上单调递增，在(x ,x )上单 1 2 4 1 1 2 调递减，在(x ,+)上单调递增，所以x 是 f(x)的极大值点，x 是 f(x)的极小值点，所以 f(x ) f(x )， 2 1 2 1 2 学科网（北京）股份有限公司所以| f(x )− f(x )|= f(x )− f(x )． 1 2 1 2 1 1−8a2 由（1）知，x x =2，x +x = ，则x −x = (x +x )2 −4x x = ． 1 2 1 2 a 2 1 1 2 1 2 a 2−16a2 2 要证| f(x )− f(x )| ，只需证 f(x )− f(x ) (x −x )． 1 2 2a 1 2 2 2 1 2 2 x x −x 因为 (x −x )− f(x )+ f(x )= (x −x )+a(x −x )−ln 2 +2a 2 1 2 2 1 1 2 2 2 1 2 1 x x x 1 1 2 2 x 2(x −x ) x −x x =2a(x −x )+ (x −x )−ln 2 = 2 1 + 2 1 −ln 2 2 1 2 2 1 x x +x x x x 1 1 2 1 2 1 x 2( 2 −1) x x x x = 1 + 2 − 1 −ln 2 ， x x x x 2 +1 1 2 1 x 1 x 2(t−1) 1 设t = 2 1，g(t)= + t − −lnt． x t+1 t 1 4 1 1 1 4 ( t −1)2 所以g(t)= + + − = + 0， (t+1)2 2 t 2t t t (t+1)2 2t t 所以g(t)在(1,+)上单调递增，所以g(t) g(1)=0． 2 2 所以 (x −x )− f(x )+ f(x )0，即得 f(x )− f(x ) (x −x )成立． 2 2 1 1 2 1 2 2 2 1 所以原不等式成立． 学科网（北京）股份有限公司