文档内容
专练 04(填空题-基础)
1.命题p:“ ”的否定是 .
【答案】
【分析】
根据特称命题“ ”的否定为全称命题“ ”即可得结果.
【详解】
因为特称命题的否定是全称命题,否定特称命题时,一是要将存在量词改写为全称量词,二是否定结论,
所以,命题p:“ ”的否定 为 ,故答案为 .
【点睛】
本题主要考查全称命题的否定,属于简单题.全称命题与特称命题的否定与命题的否定有一定的区别,否定
全称命题和特称命题时,一是要改写量词,全称量词改写为存在量词、存在量词改写为全称量词;二是要否
定结论,而一般命题的否定只需直接否定结论即可.
2.已知 ,则 的值为___________.
【答案】
【解析】
试题分析:对 分子分母同时除以 得到 ,解得 .
考点:同角三角函数关系.
【思路点晴】本题主要考查同角三角函数关系,考查正弦余弦和正切的相互转化问题.由于已知条件的分子和分母都是次数为 的表达式,所以我们可以分子分母同时除以 得到
,即 ,就将正弦和余弦,转化为正切了.如果分子分母都是二次的,则需同
时除以 来转化为正切.
3.函数 的定义域是 .
【答案】
【解析】
解:因为 ,故定义域为
4.计算: ______.
【答案】
【分析】
直接利用公式计算得到答案.
【详解】
故答案为【点睛】
本题考查了指数对数的计算,属于简单题目.
5.满足 的集合 的个数是______.
【答案】3
【分析】
列举满足条件得到集合得到答案.
【详解】
,则满足条件的集合有: 、 、 .
故答案为:3.
【点睛】
本题考查了根据集合的包含关系求集合,属于简单题.
6.函数 是定义在 上的奇函数,当 , ,则函数解析式 .
【答案】
【分析】
根据已知条件和奇函数的性质,易求出函数的解析式,最后表示成分段函数即可.
【详解】
是定义在R上的奇函数, ,
当 时, ,则 , 当 时, ,
.所以本题答案为 .
【点睛】
本题考查的知识点是函数奇偶性的性质,要求学生会根据函数奇偶性的性质,结合已知条件求出函数的解
析式,注意解析式是否是分段函数,属基础题.
7.设 为定义在R上的奇函数,当 时, (b为常数),则 ______.
【答案】-1
【分析】
由 为定义在R上的奇函数,则 ,得 ,由 ,代入求值即可.
【详解】
解:∵ 为定义在R上的奇函数,∴ ,
当 时, (b为常数),∴ ,得 ,
即当 时, ,则 ,
故答案为:-1.
【点睛】
本题考查了函数的奇偶性,重点考查了函数求值问题,属基础题.
8.集合 中至多有一个元素的充要条件是_____.【答案】 或
【分析】
集合 中至多有一个元素等价于方程 至多一个根,利用判别式求解
即可,另外当 单独进行验证。
【详解】
解:由已知得方程 至多一个根,
或 ,解得
故答案为 或
【点睛】
本题考查二次方程根的个数,关键注意要对二次项系数是否为零进行讨论,本题是基础题。
9.若函数 有零点,则实数k的取值范围是________.
【答案】(0,1]
【分析】
依据题意可得 ,然后简单计算即可.
【详解】
有零点,即k∈而-|x|≤0,0< ≤20=1,∴ 的值域为(0,1].
所以k的取值范围是(0,1]
故答案为:(0,1]
【点睛】
本题考查依据函数有零点求参数,本题难点能得到 ,属基础题.
10.若幂函数 在 上为减函数,则实数m的值是______.
【答案】
【分析】
根据幂函数的定义以及单调性列式求得 的值.
【详解】
因为函数 既是幂函数又是 的减函数,
所以 ,解得: .
故答案为: .
【点睛】
本小题主要考查幂函数的定义以及单调性,属于基础题.
11.已知 且 若 恒成立,则实数m的取值范围是_________.
【答案】
【解析】试题分析:因为 且
所以, 2+2=4,又 恒成立,所以实数m的取值范围是
。
考点:本题主要考查均值定理的应用。
点评:典型题,关键是由 进一步应用均值定理。
12.已知 是定义在 上的奇函数,且在 上是减函数, ,则满足 的实数
的取值范围是_______.
【答案】
【分析】
利用函数奇偶性可得 ,则将不等式转化为 ,再利用函数的单调性列不等式
求解即可.
【详解】
因为 是定义在 上的奇函数,且在 上是减函数, ,
所以 .因为 ,所以 ,
所以 ,解得 .故答案为: .
【点睛】本题考查函数奇偶性,单调性的综合应用,考查抽象函数不等式的求解,是基础题.
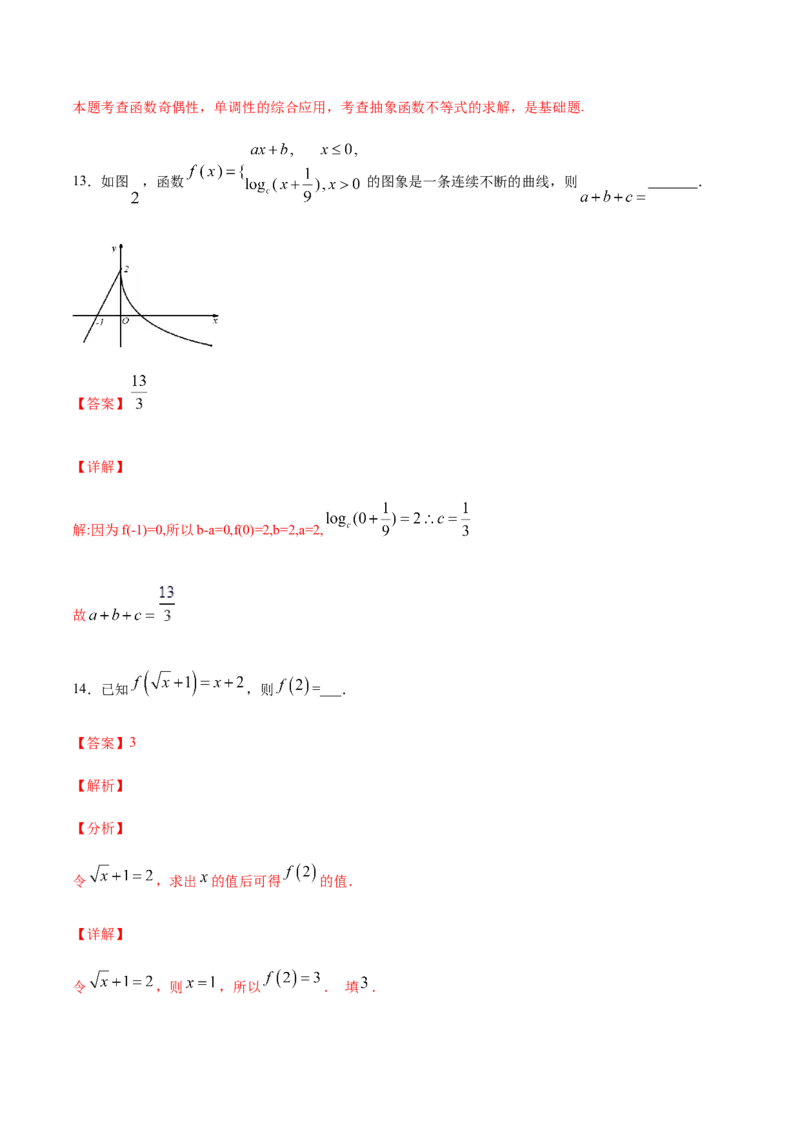
13.如图 ,函数 的图象是一条连续不断的曲线,则 .
【答案】
【详解】
解:因为f(-1)=0,所以b-a=0,f(0)=2,b=2,a=2,
故
14.已知 ,则 =___.
【答案】3
【解析】
【分析】
令 ,求出 的值后可得 的值.
【详解】
令 ,则 ,所以 . 填 .【点睛】
本题考查函数的函数值的求法,注意无需求出解析式,可整体考虑.
15.若 是偶函数,则 _______________.
【答案】
【分析】
根据 为偶函数则 ,由此求得 的值.
【详解】
由于 为偶函数,所以 ,即 ,即
,即 ,即
,所以 , .
故答案为:
【点睛】
本小题主要考查根据函数的奇偶性求参数,属于基础题.
16. , , ,则 从小到大的关系是______.
【答案】
【详解】【分析】
根据指数、对数函数的性质,可得 ,从而得出 的大小关系.
【详解】
因为 ,所以 ,
因为 ,所以 ,
因为 ,所以 ,
∴ .
故答案为: .
【点睛】
考查指数函数、对数函数的单调性,对数的运算,还考查了转化问题的能力,属于基础题 .
17.若函数 ( 且 )在 上最大值是最小值的2倍,则 ______.
【答案】2或
【分析】
将 分成 两种情况,根据 的单调性以及函数最大值是最小值的两倍列方程,解方程求
得 的值.
【详解】当 时,函数 为 上的减函数,故 ,即 ,解得 .
当 时,函数 为 上的增函数,故 ,即 ,解得 .
故 的值为 或 .
故填: 或 .
【点睛】
本小题主要考查指数函数的单调性和最值,考查分类讨论的数学思想方法,属于基础题.
18.已知函数 在 是增函数,则实数 的取值范围是______.
【答案】
【分析】
对 分 和 两种情况结合复合函数的单调性讨论得解.
【详解】
当 时, ,显然在 不是增函数,所以舍去;
当 时,由题得 ,所以 .
所以实数a的取值范围为 .故答案为
【点睛】
本题主要考查复合函数的单调性问题,考查二次函数的单调性,意在考查学生对这些知识的理解掌握水平.
19.已知 是函数 的零点,若 ,则 的值满足________(与零的关系).
【答案】
【解析】
易知函数 单调递增,且 ,
所以当 时, .
即 .
20.已知 为偶函数,且在 上单调递减,则满足 的 的取值范围是
______.
【答案】
【分析】
利用函数的奇偶性、单调性去掉不等式中的符号“ ”,转化为具体不等式即可求解.
【详解】
因为 为偶函数,所以 可化为 , 又 在 上单调递减,所以 在 上单调递增,所以 ,解得 .
故答案为: .
【点睛】
本题考查函数的奇偶性、单调性及其应用,考查抽象不等式的求解,考查学生灵活运用知识解决问题的能
力.
21.已知 ,则 ________.
【答案】1
【分析】
求出 , ,然后求解表达式的值.
【详解】
解: ,可得 , , ,
故答案为:1.
【点睛】
本题主要考查对数的运算法则的应用,属于基础题.
22.计算: ______.
【答案】80
【分析】
根据指数幂与根式的互化,由指数运算法则,以及对数运算法则,直接计算,即可得出结果.【详解】
.
故答案为: .
【点睛】
本题主要考查指数幂与对数的运算,熟记运算法则即可,属于基础题型.
23.若 对一切实数 都成立,则实数 的取值范围是______.
【答案】
【分析】
对一切实数 都成立,即 ,再求出 的范围即得解.
【详解】
对一切实数 都成立,即
因为 ,所以 ,
所以 .
故答案为:
【点睛】
本题主要考查不等式的恒成立问题,考查指数函数的性质,意在考查学生对这些知识的理解掌握水平.
24.已知 是定义在 上的偶函数,则 ______.【答案】
【分析】
根据偶函数的性质可知其定义域关于原点对称,解出 的值,然后利用偶函数的定义 求解
,然后得出 的值.
【详解】
因为函数 是定义在 上的偶函数,所以 ,解得 ,
又 得 .所以 .
故答案为: .
【点睛】
本题考查根据函数的奇偶性求参数的值,属于简单题.
25.已知函数 ,若 ,则 __________.
【答案】
【分析】
由已知条件可求 的值,进而可求出 的值.
【详解】
解:由题意知则 .
故答案为:-26.
【点睛】
本题考查了整体代入的思想.这类题的做题思路有两种,一是根据函数的奇偶性进行求值,二是本题采取的代
入 的值,整体代入进行求值.
26.已知扇形的弧长为6,圆心角弧度数为3,则其面积为______________;
【答案】6
【分析】
根据扇形面积公式 求解即可.
【详解】
扇形的弧长为6,圆心角弧度数为3,则扇形的半径 ,所以该扇形的面积 .
故答案为:6
【点睛】
此题考查求扇形的面积,根据圆心角、半径、弧长的关系求解.
27.已知 , ,则 __________.
【答案】
【分析】将 和 分别平方,再求和,即可得出 .
【详解】
解:∵ ,两边同时平方得 ,
又 ,同理得 ,
两式相加得 ,
化简得 ,
∴ ,
∴ ,
故答案为: .
【点睛】
本题主要考查两角差的余弦公式得应用,考查整体思想,属于基础题.
28.当 时, 的最小值为______.
【答案】
【分析】将所求代数式变形为 ,然后利用基本不等式可求得所求代数式的最小值.
【详解】
, ,由基本不等式得 .
当且仅当 时,等号成立.因此, 的最小值为 .
故答案为: .
【点睛】
本题考查利用基本不等式求代数式的最值,考查计算能力,属于基础题.
29.函数 的最大值为________.
【答案】
【分析】
利用诱导公式和二倍角公式化简 ,由此求得 的最大值.
【详解】
依题意 ,所以 的最大值为 .
故答案为:
【点睛】本小题主要考查诱导公式和二倍角公式,考查三角函数最大值的求法,属于基础题.
30.已知函数f(x)= 在区间[0,2]上单调递减,则a的取值范围是______.
【答案】
【分析】
由题意利用函数的单调性的性质可得可得 ,由此求得a的范围.
【详解】
解:根据函数f(x)= 在区间[0,2]上单调递减,可得 ,
求得 ,
故答案为: .
【点睛】
本题主要考查函数的单调性的性质,函数的定义域,属于基础题.