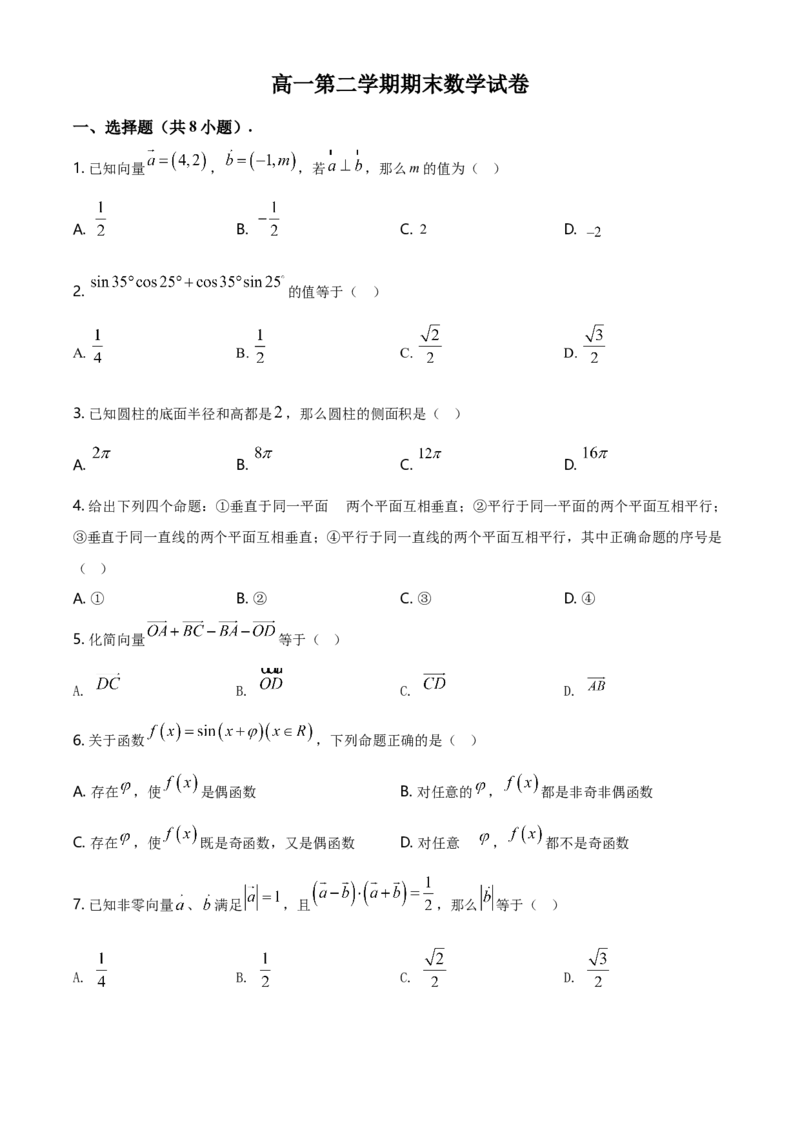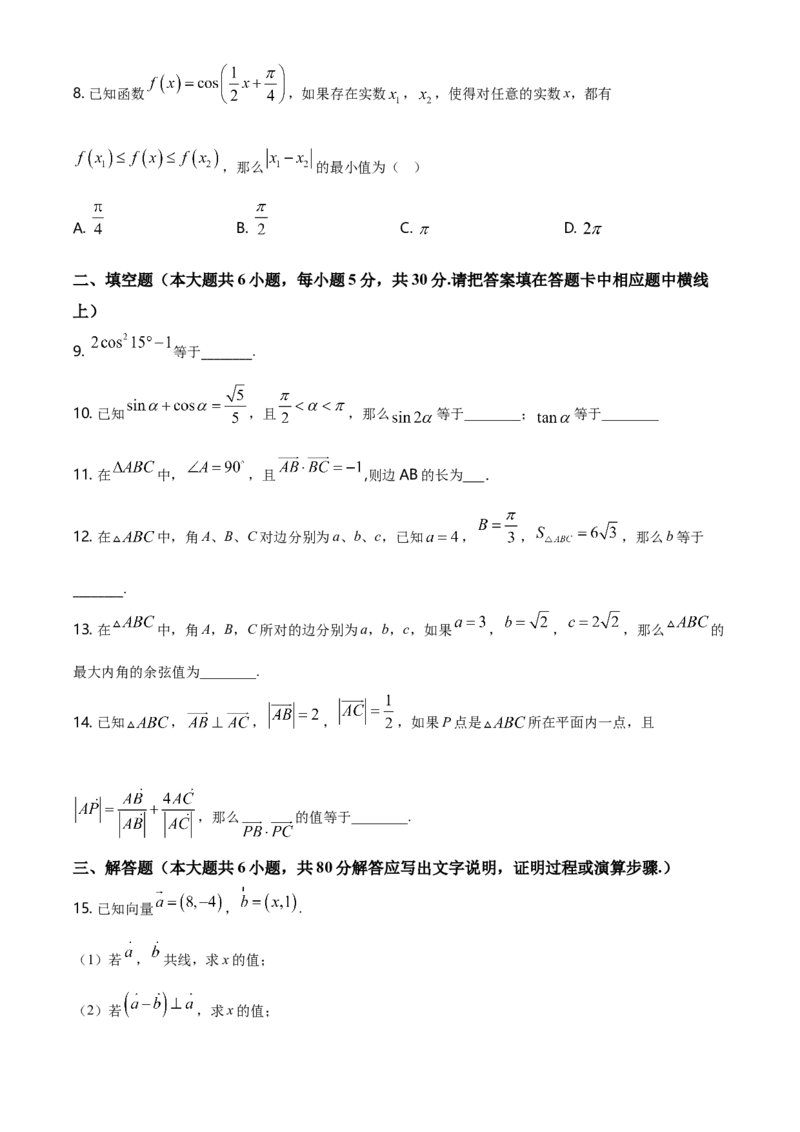文档内容
高一第二学期期末数学试卷
一、选择题(共8小题).
1. 已知向量 , ,若 ,那么m的值为( )
A. B. C. 2 D.
2. 的值等于( )
A. B. C. D.
3. 已知圆柱的底面半径和高都是 ,那么圆柱的侧面积是( )
A. B. C. D.
4. 给出下列四个命题:①垂直于同一平面 的两个平面互相垂直;②平行于同一平面的两个平面互相平行;
③垂直于同一直线的两个平面互相垂直;④平行于同一直线的两个平面互相平行,其中正确命题的序号是
( )
A. ① B. ② C. ③ D. ④
5. 化简向量 等于( )
A. B. C. D.
6. 关于函数 ,下列命题正确的是( )
A. 存在 ,使 是偶函数 B. 对任意的 , 都是非奇非偶函数
C. 存在 ,使 既是奇函数,又是偶函数 D. 对任意 的, 都不是奇函数
7. 已知非零向量 、 满足 ,且 ,那么 等于( )
A. B. C. D.8. 已知函数 ,如果存在实数 , ,使得对任意的实数x,都有
,那么 的最小值为( )
A. B. C. D.
二、填空题(本大题共6小题,每小题5分,共30分.请把答案填在答题卡中相应题中横线
上)
9. 等于________.
.
10. 已知 ,且 ,那么 等于________; 等于________
11. 在 中, ,且 ,则边AB的长为 .
12. 在 中,角A、B、C对边分别为a、b、c,已知 , , ,那么b等于
________.
13. 在 中,角A,B,C所对的边分别为a,b,c,如果 , , ,那么 的
最大内角的余弦值为________.
14. 已知 , , , ,如果P点是 所在平面内一点,且
,那么 的值等于________.
三、解答题(本大题共6小题,共80分解答应写出文字说明,证明过程或演算步骤.)
15. 已知向量 , .
(1)若 , 共线,求x的值;
(2)若 ,求x的值;(3)当 时,求 与 夹角 的余弦值.
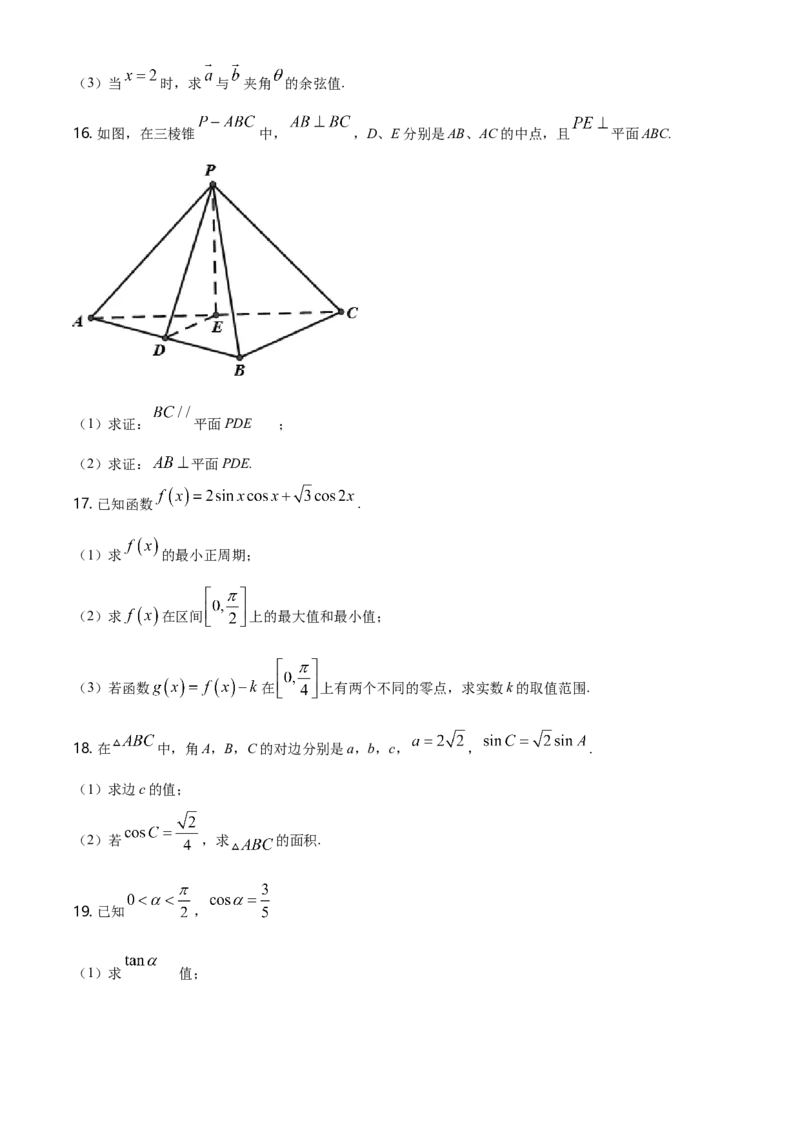
16. 如图,在三棱锥 中, ,D、E分别是AB、AC的中点,且 平面ABC.
(1)求证: 平面PDE ;
(2)求证: 平面PDE.
17. 已知函数 .
(1)求 的最小正周期;
(2)求 在区间 上的最大值和最小值;
(3)若函数 在 上有两个不同的零点,求实数k的取值范围.
18. 在 中,角A,B,C的对边分别是a,b,c, , .
(1)求边c的值;
(2)若 ,求 的面积.
.
19. 已知 ,
(1)求 的值;(2)求 的值;
(3)若 且 ,求 的值.
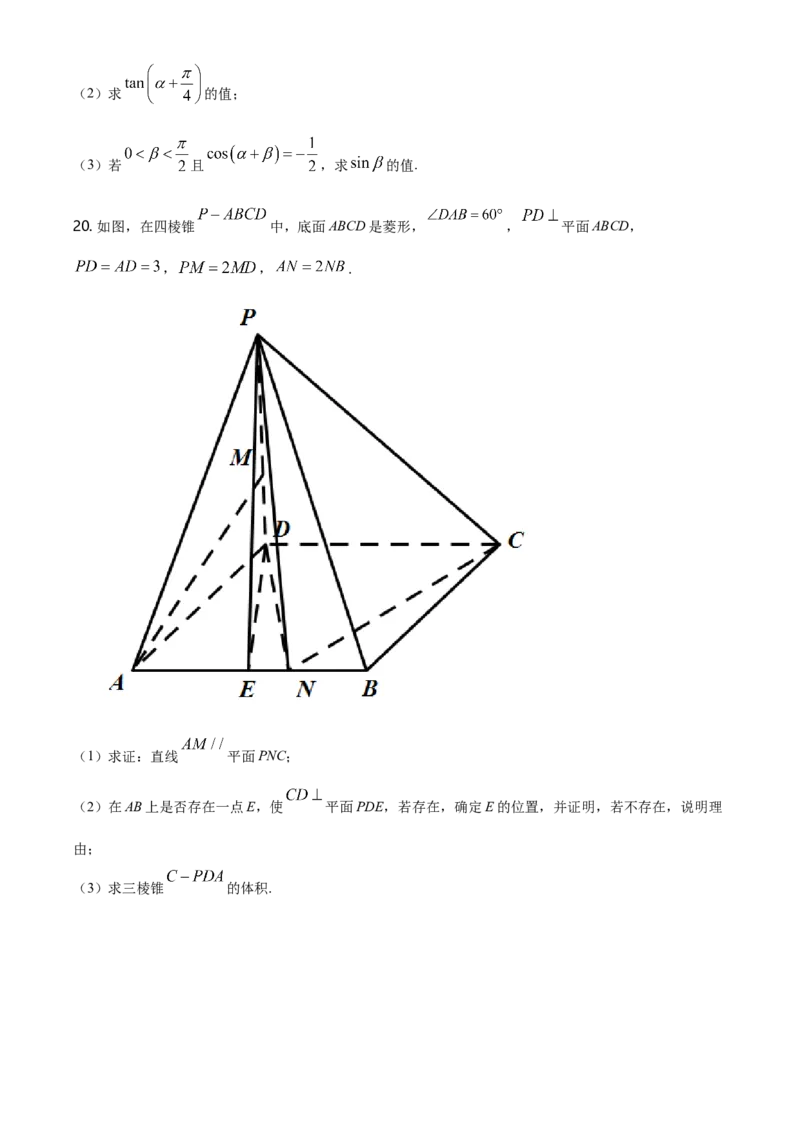
20. 如图,在四棱锥 中,底面ABCD是菱形, , 平面ABCD,
, , .
(1)求证:直线 平面PNC;
(2)在AB上是否存在一点E,使 平面PDE,若存在,确定E的位置,并证明,若不存在,说明理
由;
(3)求三棱锥 的体积.