文档内容
领取更多免费资料关注微信公众号:网盘网课资源
决胜 2024 年高考数学押题预测卷 06
数 学
(新高考九省联考题型)
(考试时间:120分钟 试卷满分:150分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己
的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.已知样本数据为 、 、 、 、 、 、 ,去掉一个最大值和一个最小值后的数据与原来
的数据相比,下列数字特征一定不变的是( )
A. 极差 B. 平均数 C. 中位数 D. 方差
【答案】C
【解析】样本数据为 、 、 、 、 、 、 ,去掉一个最大值和一个最小值后的数据与原
来的数据相比,假设从小到大就是从 到 ,极差可能变化,故A错;
平均数为 ,可能变,故B错;
中位数还是按从小到大排序中间位置的数,故C正确;
方差为 ,有可能变,故D错.
故选:C
2.已知全集 ,集合A,B满足 ,则下列关系一定正确的是( )
.
A B. C. D.
【答案】C
【解析】因为集合A,B满足 ,故可得 ,
对A:当 为 的真子集时,不成立;
对B:当 为 的真子集时,也不成立;
对C: ,恒成立;
对D:当 为 的真子集时,不成立;
故选:C.
3. , 的展开式中 项的系数等于40,则 是 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
【答案】A
【解析】 的展开式中含 项为 ,
故 ,解得 ,
1领取更多免费资料关注微信公众号:网盘网课资源
故“ ”是“ ”的充分不必要条件.
故选:A
4.若 ,则 ( )
A. B. C. 2 D.
【答案】C
【解析】由 ,得 ,
即 ,即 ,
所以 ,所以 ,
则 .
故选:C.
5.在平面直角坐标系xOy中,已知向量 与 关于x轴对称,向量 若满足
的点A的轨迹为E,则( )
A. E是一条垂直于x轴的直线 B. E是一个半径为1的圆
C. E是两条平行直线 D. E 是椭圆
【答案】B
【解析】设 ,由题有 , ,
所以 , ,
所以 ,即 ,
所以点 的集合是以 为圆心,1为半径的圆.
其轨迹 为半径为1的圆,
故选:B.
6.夹弹珠游戏是儿童特别喜欢的游戏,夹弹珠能有效提高参与者的注意力与协调性,调整逻辑思维判
断和空间控制平衡能力,锻炼小肌肉,增强手眼协调,培养敏捷的反应能力,从而提高参与者的适应
能力.如图,三个半径都是 的玻璃弹珠放在一个半球面形状的容器(不计厚度)中,每颗弹珠的
顶端恰好与容器的上沿处于同一水平面,则这个容器的表面积(包括容器的内部和外部两部分)是(
)
A. B. C. D.
【答案】D
【解析】 在面 上的投影为 为大球球心, 为小球球心.
2领取更多免费资料关注微信公众号:网盘网课资源
,大球半径为 ,
,
,
故选:D.
7.已知函数 , , ,若
的最小值为 ,且 ,则 的单调递增区间为( )
A. B.
C. D.
【答案】B
【解析】因为 ,
又 , ,且 的最小值为 ,
所以 ,即 ,又 ,所以 ,
所以 ,又 ,所以 ,即 ,
因为 ,所以 ,
所以 ,令 , ,
解得 , ,
所以函数 的单调递增区间为 .
故选:B
3领取更多免费资料关注微信公众号:网盘网课资源
8.已知 , 是椭圆和双曲线的公共焦点,P,Q是它们的两个公共点,且P,Q关于原点对称,
若椭圆的离心率为 ,双曲线的离心率为 ,则 的最小值是( )
A. B. C. D.
【答案】A
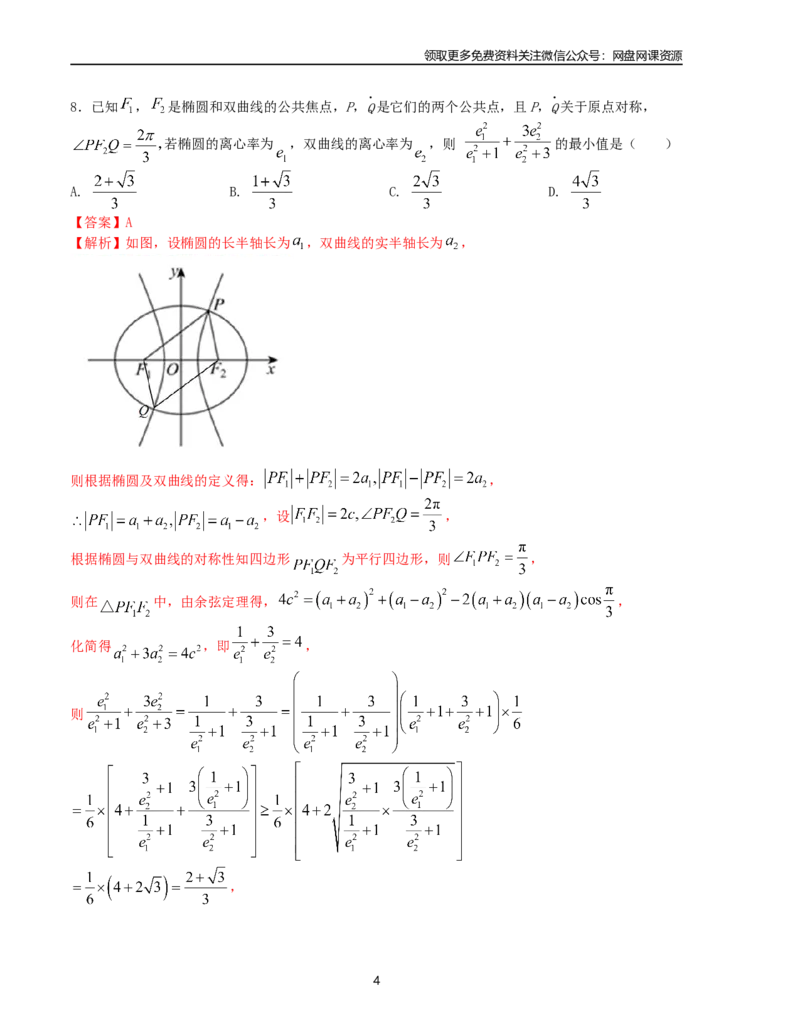
【解析】如图,设椭圆的长半轴长为 ,双曲线的实半轴长为 ,
则根据椭圆及双曲线的定义得: ,
,设 ,
根据椭圆与双曲线的对称性知四边形 为平行四边形,则 ,
则在 中,由余弦定理得, ,
化简得 ,即 ,
则
,
4领取更多免费资料关注微信公众号:网盘网课资源
当且仅当 ,即 时等号成立,
故选:A.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知复数z在复平面内对应的点为 ,则( )
A. B. C. D.
【答案】ACD
【解析】由题可知, , ,故A正确;
, ,故B错误;
,所以 ,C正确;
,
所以 ,故D正确.
故选:ACD
10.设 是一个随机试验中的两个事件,且 ,则( )
A. B.
C. D.
【答案】ACD
【解析】 ,故A对.
,故B错.
,故C对.
5领取更多免费资料关注微信公众号:网盘网课资源
,
,故D对.
故选:ACD.
11 . 已 知 定 义 在 上 的 函 数 , 其 导 函 数 分 别 为
,且 ,
则( )
A. 的图象关于点 中心对称 B.
C. D.
【答案】BCD
【解析】由题意可得 ,两式相减可得 ①,
所以 的图象关于点 中心对称,A错误;
由 ②,②式两边对 求导可得 ,可知 是偶函数,
以 替换①中的 可得 ,
可得 ,所以 是周期为4的周期函数,B正确;
因为 ,可知 也是周期为4的周期函数,即 ,
两边求导可得 ,所以 ,C正确;
因为 ,令 ,则 ,即 ,
又因为 是偶函数,所以 ,
又因为 是周期为4的周期函数,则 ,
由 可得 ,
所以 ,D正确.
故选:BCD
三、填空题:本题共3小题,每小题5分,共15分.
12.等差数列 的首项为 1,公差不为 0,若 成等比数列,则 的前 5 项的和为
__________.
【答案】
【解析】设等差数列 的公差为 且 ,且 ,
因为 成等比数列,可得 ,即 ,
即 或 (舍去),
6领取更多免费资料关注微信公众号:网盘网课资源
所以 .
故答案为:
13.已知圆锥的母线长为2,则当圆锥的母线与底面所成的角的余弦值为__________时,圆锥的体积最
大,最大值为__________.
【答案】 ;
【解析】设圆锥的底面半径r,母线为l,高为h,
设母线与底面所成的角为 ,
则 ,
则 ,
则 ,
则圆锥的体积为
,
令 ,则 ,
令 ,求导得 ,
令 ,则 或 舍去 ,
所以当 时, , 单调递增,
当 时, , 单调递减,
所以当 时, 取得极大值,也是最大值.
此时 最大, ,
即圆锥的母线与底面所成的角的余弦值 时,
圆锥的体积最大,最大值为
故答案为: ;
14.在 中,角 所对的边分别为 ,若 分别在边
7领取更多免费资料关注微信公众号:网盘网课资源
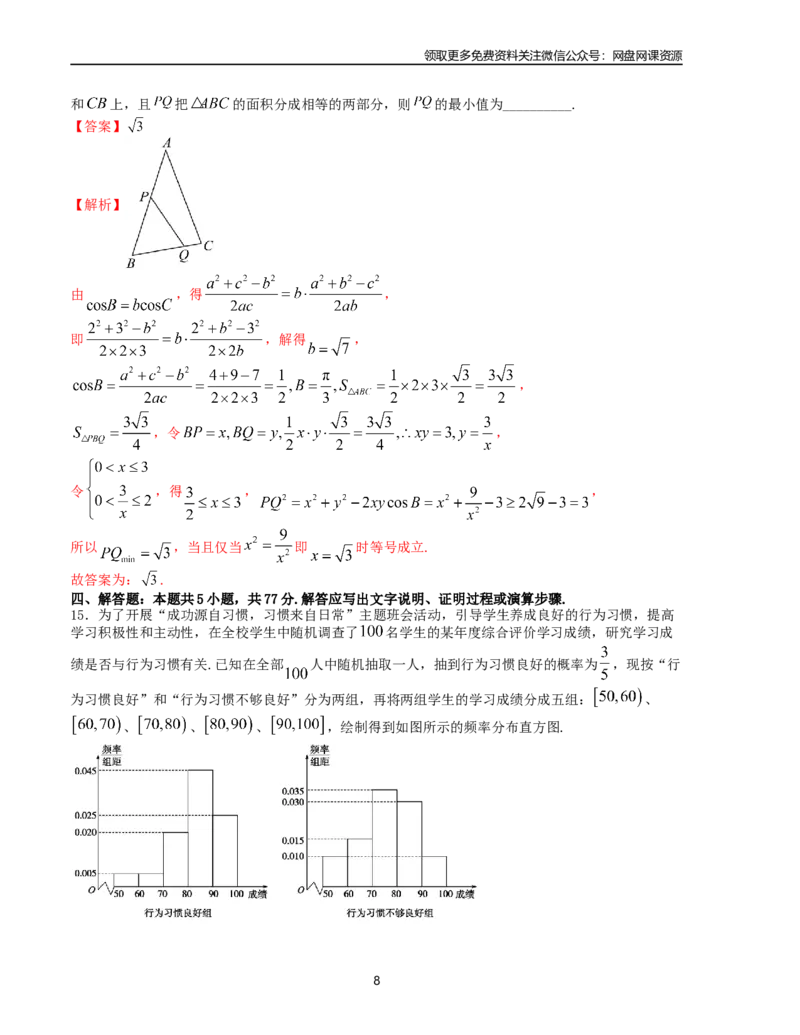
和 上,且 把 的面积分成相等的两部分,则 的最小值为__________.
【答案】
【解析】
由 ,得 ,
即 ,解得 ,
,
,令 ,
令 ,得 , ,
所以 ,当且仅当 即 时等号成立.
故答案为: .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.为了开展“成功源自习惯,习惯来自日常”主题班会活动,引导学生养成良好的行为习惯,提高
学习积极性和主动性,在全校学生中随机调查了 名学生的某年度综合评价学习成绩,研究学习成
绩是否与行为习惯有关.已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为 ,现按“行
为习惯良好”和“行为习惯不够良好”分为两组,再将两组学生的学习成绩分成五组: 、
、 、 、 ,绘制得到如图所示的频率分布直方图.
8领取更多免费资料关注微信公众号:网盘网课资源
(1)若规定学习成绩不低于 分为“学习标兵”,请你根据已知条件填写下列 列联表,并判断
是否有 的把握认为“学习标兵与行为习惯是否良好有关”;
行为习惯良好 行为习惯不够良好 总计
学习标兵
非学习标兵
总计
(2)现从样本中学习成绩低于 分的学生中随机抽取 人,记抽到的学生中“行为习惯不够良好”
的人数为 ,求 的分布列和期望.
参考公式与数据: ,其中 .
【答案】(1)列联表见解析,有 (2)分布列见解析,
【解析】(1)已知在全部 人中随机抽取一人,抽到行为习惯良好的概率为 ,
则 名学生中,行为习惯良好的有 人,行为习惯不够良好的有 人.
由频率分布直方图可知,行为习惯良好组中不低于 分的学生有 人,
行为习惯不够良好组中不低于 分的学生有 人
则 列联表为:
行为习惯良好 行 为习惯不够良好 总计
学习标兵
非学习标兵
总计
, ,
因为 ,所以有 的把握认为“学习标兵与行为习惯是否良好有关”.
(2)行为习惯良好组中低于 分的学生有 人,
行为习惯不够良好组中低于 分的学生有 人,则 的可能值为 、 、 ,
9领取更多免费资料关注微信公众号:网盘网课资源
, , .
的分布列为:
期望 .
16.已知 .
(1)若 在 恒成立,求a的范围;
(2)若 有两个极值点s,t,求 的取值范围.
【答案】(1) (2)
【解析】(1)由函数 ,因为 在 上恒成立,
即 在 恒成立,
令 ,可得 ,
令 ,可得 ,
所以 在 单调递减,所以 ,
所以 恒成立,所以 在 单调递减,所以 ,
所以 ,所以实数 的取值范围为 .
(2)因为 有两个极值点 ,
可得 是 的两不等正根,
即 是 的两不等正根,则满足 ,解得 ,
则
,
10领取更多免费资料关注微信公众号:网盘网课资源
所以 的取值范围为 .
17.如图,在三棱锥 中, 和 都是正三角形,E是 的中点,点F满足
.
(1)求证:平面 平面 ;
(2)若 ,且 平面 ,求 的长.
【答案】(1)证明见解析 (2)6
【解析】(1)如图,连接 ,因为 ,所以 .所以A,E,D,F四点共面.
因为在三棱锥 中, 和 都是正三角形,E是 的中点,
所以 , .因为 平面 , ,所以 平面 ,
又 平面 ,所以平面 平面 .
(2)如图,记 的中心为O,连接 ,由(1)得 .同理可证 ,
且 ,所以 平面 ,以O为坐标原点,建立如图所示的空间直角坐标系.
因为 是正三角形, ,所以 , , .
所以 , , , , .
所以 , .
设平面 的一个法向量为 ,则 ,即 ,
令 ,则 , ,所以 .
因为 , ,
所以 .
因为 平面 ,所以 ,
即 ,解得 ,
11领取更多免费资料关注微信公众号:网盘网课资源
此时 .故DF的长为6.
18.已知抛物线 的焦点为 各顶点均在 上,且 .
(1)证明: 是 的重心;
(2) 能否是等边三角形?并说明理由;
(3)若 均在第一象限,且直线 的斜率为 ,求 的面积.
【答案】(1)证明见解析 (2)不肯能,理由见解析 (3)
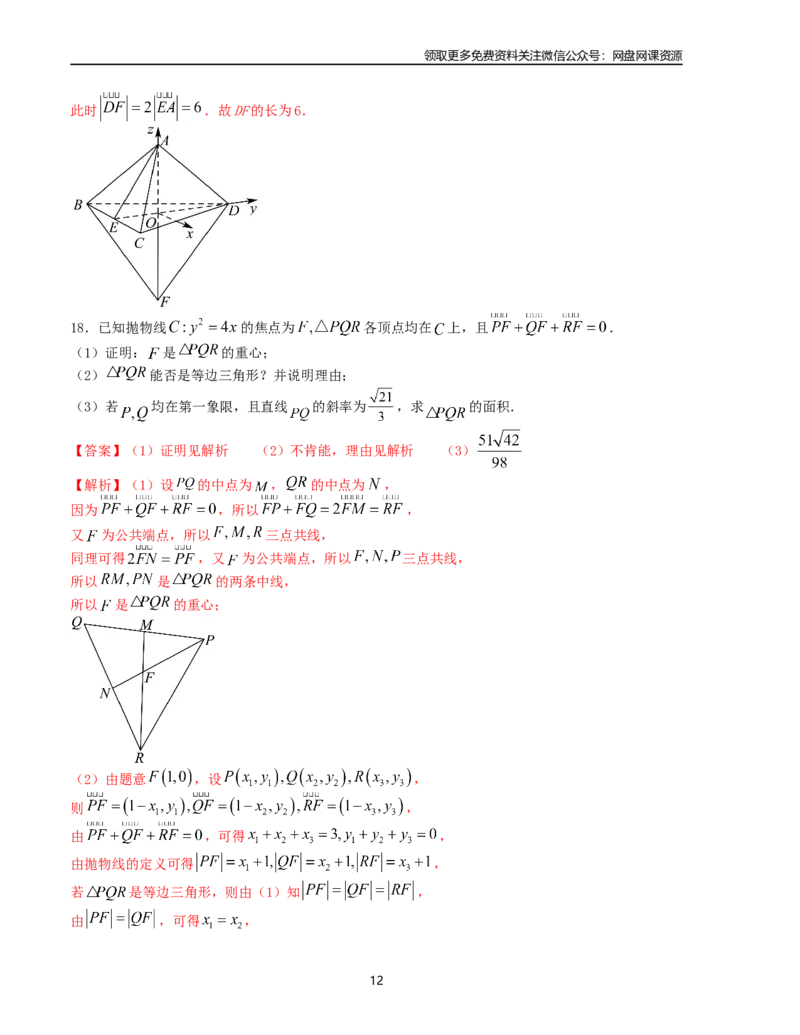
【解析】(1)设 的中点为 , 的中点为 ,
因为 ,所以 ,
又 为公共端点,所以 三点共线,
同理可得 ,又 为公共端点,所以 三点共线,
所以 是 的两条中线,
所以 是 的重心;
(2)由题意 ,设 ,
则 ,
由 ,可得 ,
由抛物线的定义可得 ,
若 是等边三角形,则由(1)知 ,
由 ,可得 ,
12领取更多免费资料关注微信公众号:网盘网课资源
又因 不重合,所以 ,
所以 ,
所以 , ,
故 ,这与 矛盾,
所以 不可能是等边三角形;
(3)设直线 的方程为 ,
联立 ,化简得 ,
,所以 ,
由韦达定理得 ,
由(2)有 ,
,所以 ,
由 得 ,解得 ,
所以 ,即 ,
直线 的方程为 ,
所以
,
13领取更多免费资料关注微信公众号:网盘网课资源
点 到直线 的距离 ,
所以 的面积为
19. 对于每项均是正整数的数列P: ,定义变换 , 将数列P变换成数列 :
.对于每项均是非负整数的数列 ,定义
,定义变换 , 将数列Q各项从大到小排列,然后去
掉所有为零的项,得到数列 .
(1)若数列 为2,4,3,7,求 的值;
(2)对于每项均是正整数的有穷数列 ,令 , .
(i)探究 与 的关系;
(ii)证明: .
【答案】(1)172; (2)(i) ;(ii)证明见解析.
【解析】(1)依题意, , ,
.
(2)(i)记 ,
,
,
,
,所以 .
(ii)设 是每项均为非负整数的数列 ,
当存在 ,使得 时,交换数列 的第 项与第 项得到数列 ,
14领取更多免费资料关注微信公众号:网盘网课资源
则 ,
当存在 ,使得 时,若记数列 为 ,则 ,
因此 ,从而对于任意给定的数列 ,
由 , ,由(i)知 ,
所以 .
15