文档内容
高一第二学期期末数学试卷
一、选择题(共10小题).
1. ( )
A. B. C. D.
2. 已知复数 ,则 的共轭复数 等于( )
A. 0 B. C. D.
3. 在 中, , , ,则 ( )
A. B. C. D.
4. 下列正确的命题的序号是( )
①平行于同一条直线的两条直线平行;
②平行于同一条直线的两个平面平行;
③垂直于同一个平面的两条直线平行;
④垂直于同一个平面 的两个平面垂直.
A. ①② B. ②④ C. ②③ D. ①③
5. 如图,在正方形 中, 是 边 的中点,设 , ,则 ( )
A. B. C. D.
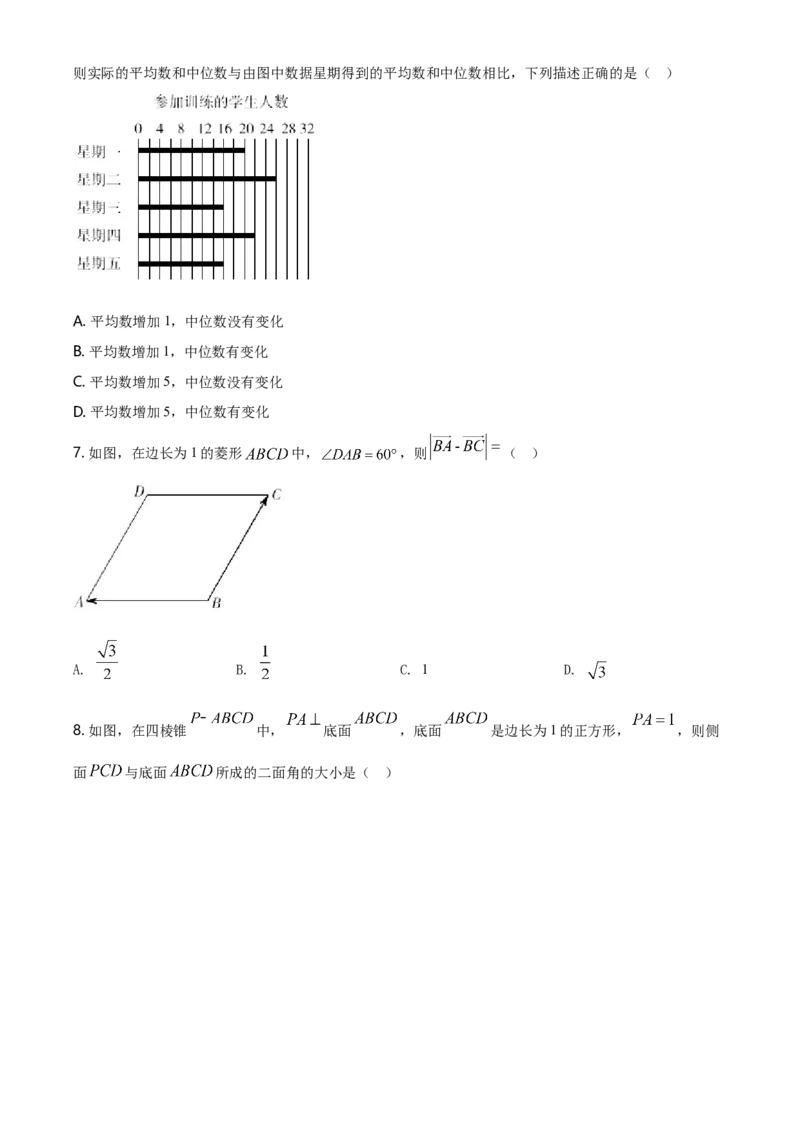
6. 如图记录了某校高一年级6月第一周星期一至星期五参加乒乓球训练的学生人数.通过图中的数据计算这
五天参加乒乓球训练的学生的平均数和中位数后,教练发现图中星期五的数据有误,实际有21人参加训练.则实际的平均数和中位数与由图中数据星期得到的平均数和中位数相比,下列描述正确的是( )
A. 平均数增加1,中位数没有变化
B. 平均数增加1,中位数有变化
C. 平均数增加5,中位数没有变化
D. 平均数增加5,中位数有变化
7. 如图,在边长为1的菱形 中, ,则 ( )
A. B. C. 1 D.
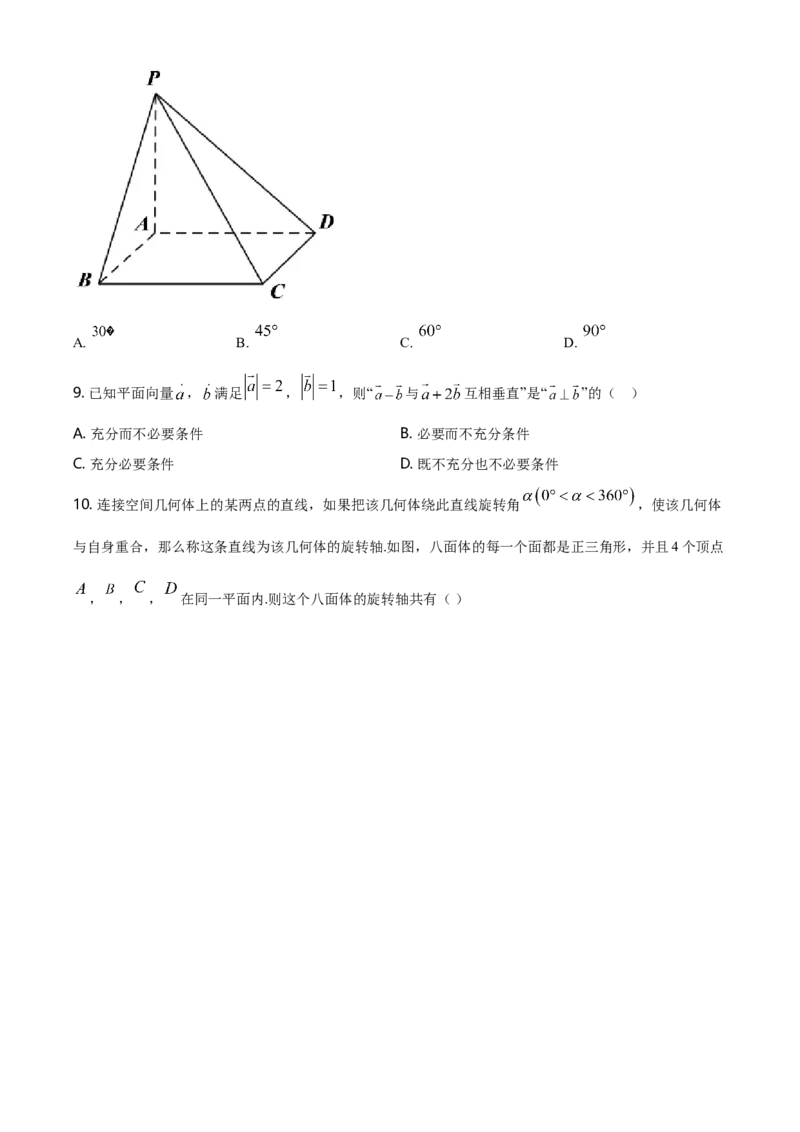
8. 如图,在四棱锥 中, 底面 ,底面 是边长为1的正方形, ,则侧
面 与底面 所成的二面角的大小是( )A. B. C. D.
9. 已知平面向量 , 满足 , ,则“ 与 互相垂直”是“ ”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
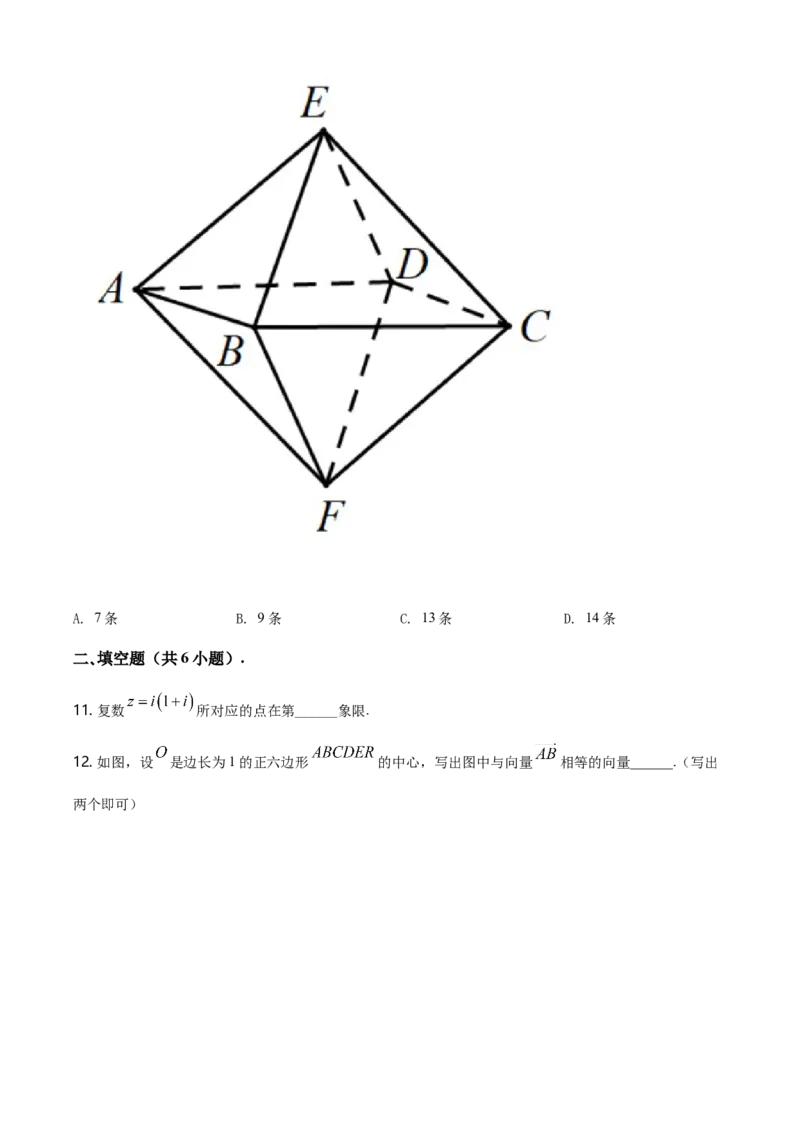
10. 连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角 ,使该几何体
与自身重合,那么称这条直线为该几何体的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点
, , , 在同一平面内.则这个八面体的旋转轴共有( )A. 7条 B. 9条 C. 13条 D. 14条
二、填空题(共6小题).
11. 复数 所对应的点在第______象限.
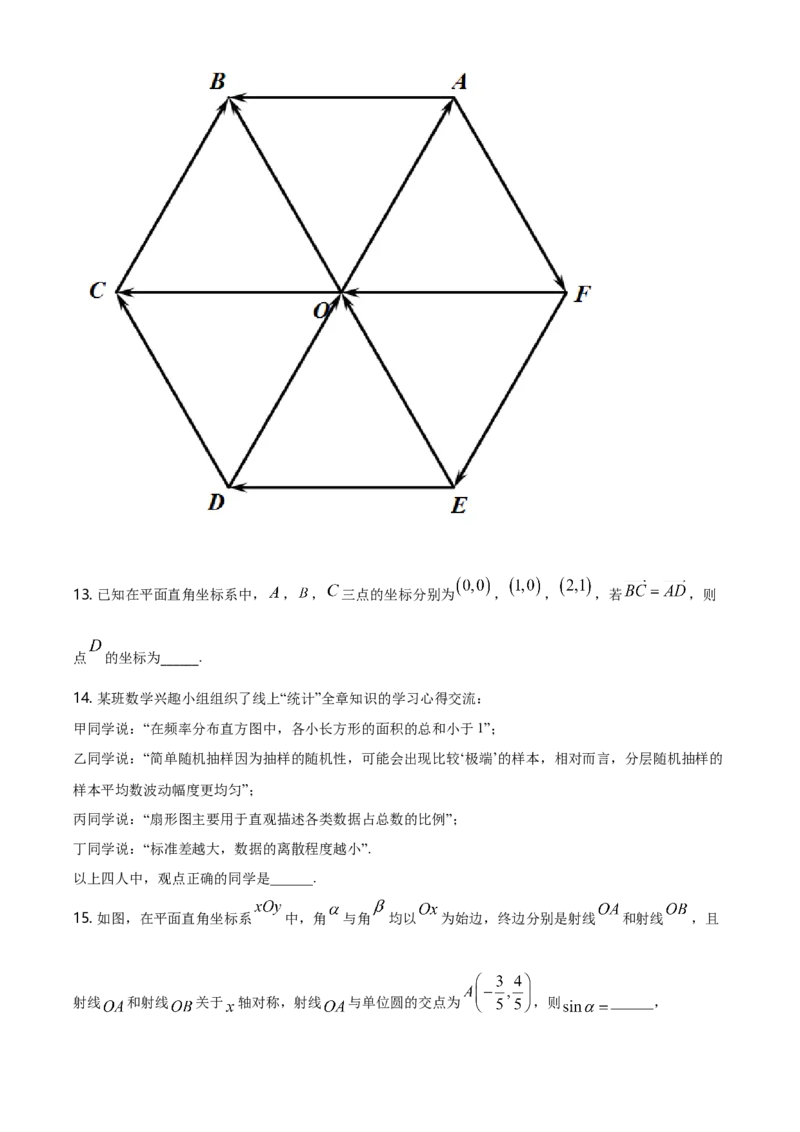
12. 如图,设 是边长为1的正六边形 的中心,写出图中与向量 相等的向量______.(写出
两个即可)13. 已知在平面直角坐标系中, , , 三点的坐标分别为 , , ,若 ,则
点 的坐标为______.
14. 某班数学兴趣小组组织了线上“统计”全章知识的学习心得交流:
甲同学说:“在频率分布直方图中,各小长方形的面积的总和小于1”;
乙同学说:“简单随机抽样因为抽样的随机性,可能会出现比较‘极端’的样本,相对而言,分层随机抽样的
样本平均数波动幅度更均匀”;
丙同学说:“扇形图主要用于直观描述各类数据占总数的比例”;
丁同学说:“标准差越大,数据的离散程度越小”.
以上四人中,观点正确的同学是______.
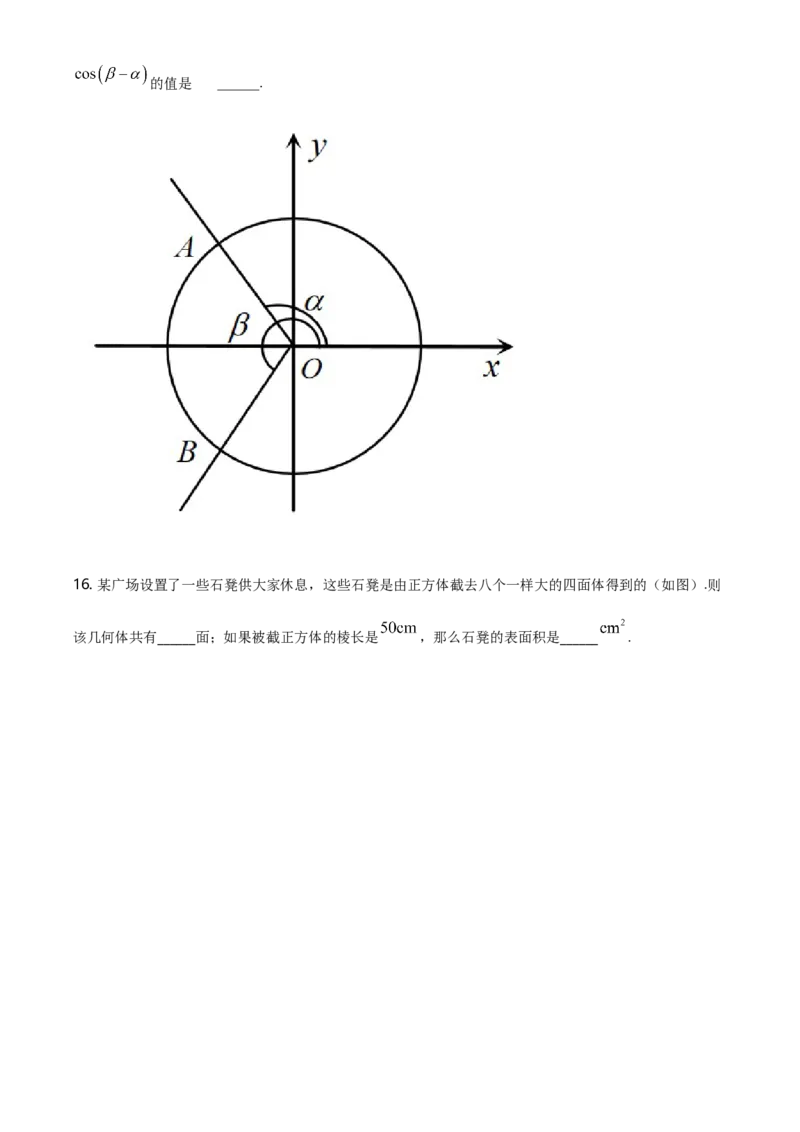
15. 如图,在平面直角坐标系 中,角 与角 均以 为始边,终边分别是射线 和射线 ,且
射线 和射线 关于 轴对称,射线 与单位圆的交点为 ,则 ______,的值是 ______.
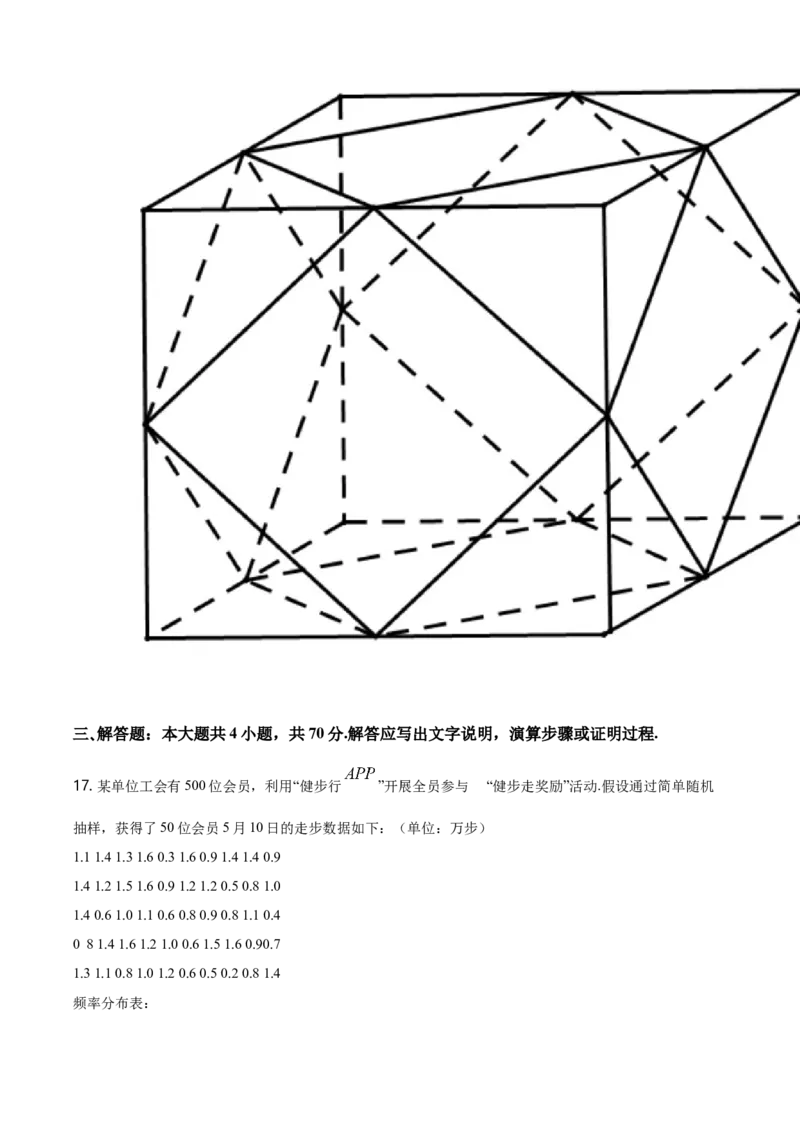
16. 某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样大的四面体得到的(如图).则
该几何体共有______面;如果被截正方体的棱长是 ,那么石凳的表面积是______ .三、解答题:本大题共4小题,共70分.解答应写出文字说明,演算步骤或证明过程.
17. 某单位工会有500位会员,利用“健步行 ”开展全员参与 的“健步走奖励”活动.假设通过简单随机
抽样,获得了50位会员5月10日的走步数据如下:(单位:万步)
1.1 1.4 1.3 1.6 0.3 1.6 0.9 1.4 1.4 0.9
1.4 1.2 1.5 1.6 0.9 1.2 1.2 0.5 0.8 1.0
1.4 0.6 1.0 1.1 0.6 0.8 0.9 0.8 1.1 0.4
.
0 8 1.4 1.6 1.2 1.0 0.6 1.5 1.6 0.90.7
1.3 1.1 0.8 1.0 1.2 0.6 0.5 0.2 0.8 1.4
频率分布表:分组 频数 频率
2 0.04
0.06
5 0.10
11 0.22
8 0.16
7 0.14
合计 50 1.00(1)写出 , , 的值;
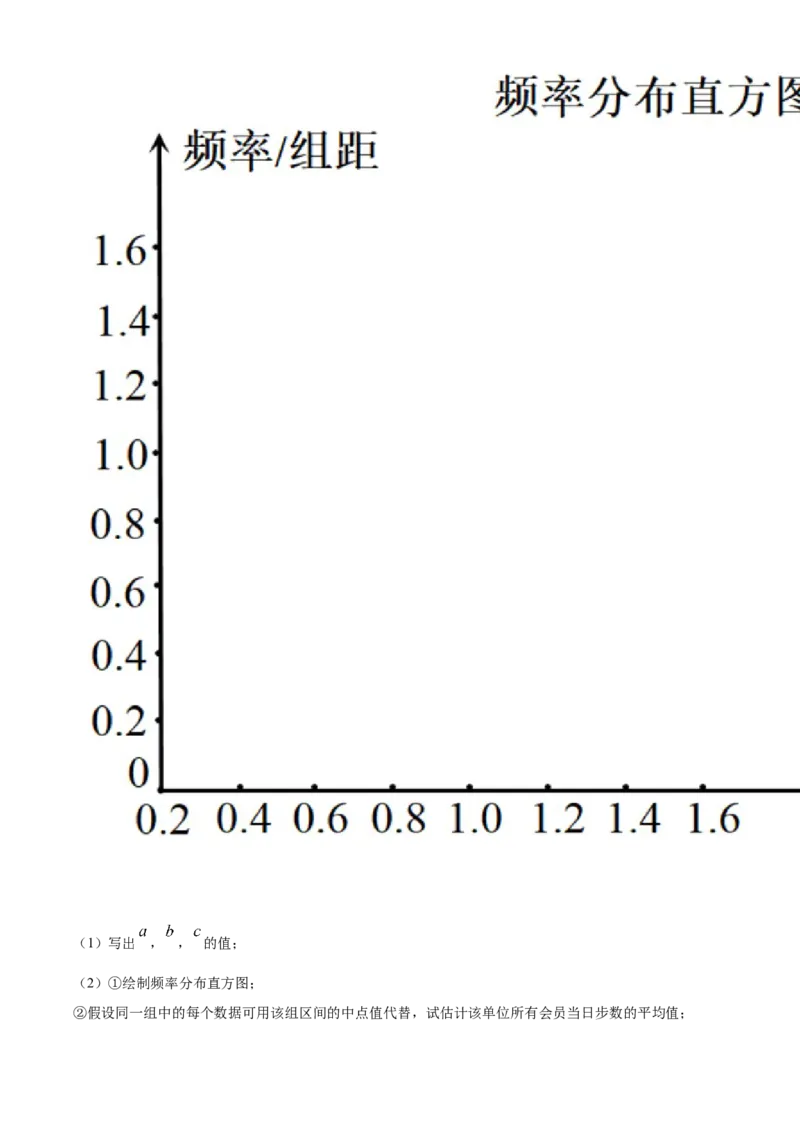
(2)①绘制频率分布直方图;
②假设同一组中的每个数据可用该组区间的中点值代替,试估计该单位所有会员当日步数的平均值;(3)根据以上50个样本数据,估计这组数据的第70百分位数.你认为如果定1.3万步为健步走获奖标准,
一定能保证该单位至少 的工会会员当日走步获得奖励吗?说明理由.
18. 在 中, , , 分别是角 , , 的对边, , .
(1)若 ,求 ;
(2)若______,求 的值及 的面积.
请从① ,② ,这两个条件中任选一个,将问题(2)补充完整,并作答.注意,只
需选择其中的一种情况作答即可,如果选择两种情况作答,以第一种情况的解答计分.
19. 已知函数 .
(1)求 的值;
(2)求 的最小正周期和单调递增区间;
(3)将函数 的图象向右平移 个单位,得到函数 的图象,若函数 在
上有且仅有两个零点,求 的取值范围.
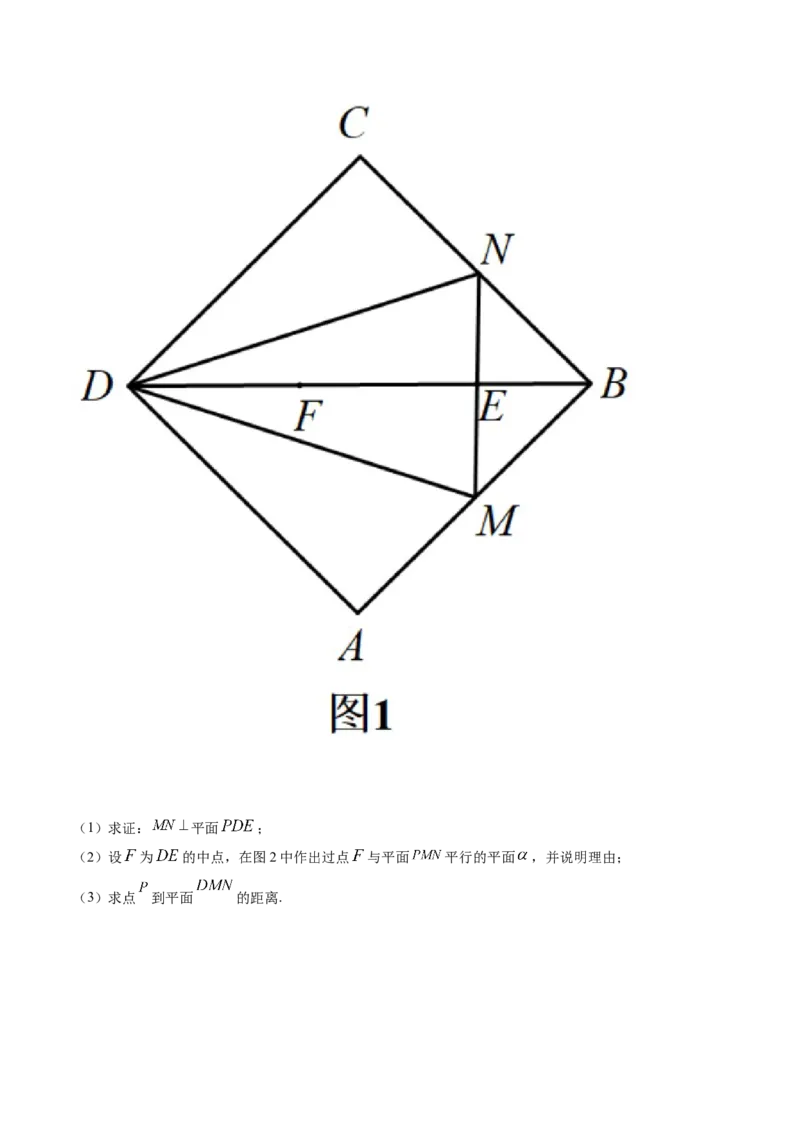
20. 如图1,设正方形 边长为1, , 分别为 , 的中点,沿 , , 把图形
折成一个四面体,使 , , 三点重合于点 ,如图2.(1)求证: 平面 ;
(2)设 为 的中点,在图2中作出过点 与平面 平行的平面 ,并说明理由;
(3)求点 到平面 的距离.