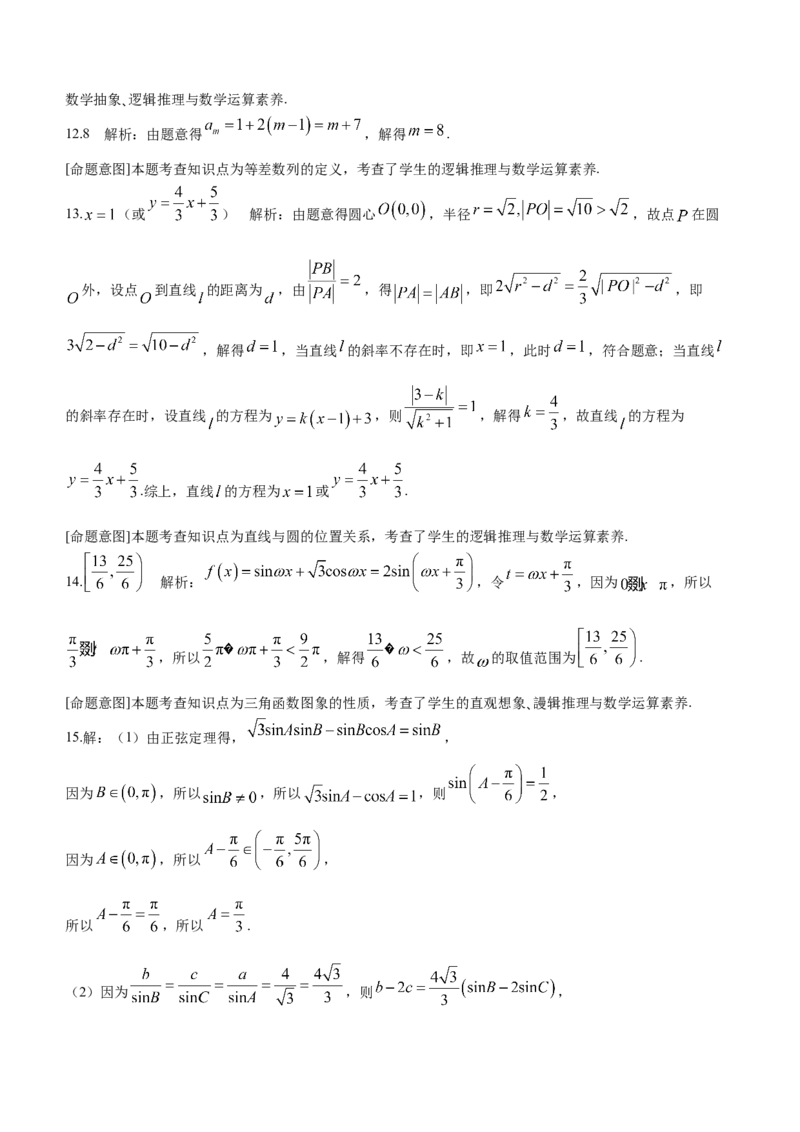文档内容
2023—2024 高三省级联测考试
数学试卷
班级__________姓名__________.
注意事项:
1.答卷前,考生务必将自己的姓名、班级和考号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷
上无效3.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符
合题目要求的.
1.已知集合 ,则 ( )
A. B. C. D.
2.已知复数 满足 ,则 ( )
A. B.
C. D.
3.将向量 绕坐标原点 逆时针旋转 得到 ,则 ( )
A.1 B.-1 C.2 D.-2
4.已知 ,则 ( )
A. B. C. D.
5.已知抛物线 的焦点为 ,准线为 是抛物线上位于第一象限内的一点,过点 作 的垂线,垂足
为 ,若直线 的倾斜角为 ,则 ( )
A.2 B. C. D.3
6.甲、乙、丙、丁4位同学报名参加学校举办的数学建模、物理探究、英语演讲、劳动实践四项活动,每人只能报其中一项,则在甲同学报的活动其他同学不报的情况下,4位同学所报活动各不相同的概率为( )
A. B. C. D.
7.已知双曲线 的左、右焦点分别为 ,过 的直线交双曲线 的右支于
两点,若 ,且 ,则双曲线 的离心率为( )
A.2 B.4 C.6 D.3
8.设 ,则下列大小关系正确的是( )
A. B.
C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要
求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知正数 满足 ,则下列选项正确的是( )
A. B.
C. D.
10.下列说法正确的是( )
A.若数据 的极差和平均数相等,则
B.数据 的第80百分位数为10.5
C.若 ,则
D.若 ,随机变量 ,则
11.如图,在棱长为1的正方体 中, 分别是 的中点, 为线段 上的动
点,则下列结论正确的是( )A.存在点 ,使得直线 与直线 为异面直线
B.存在点 ,使得
C.若 为线段 的中点,则三棱锥 与三棱锥 体积相等
D.过 三点的平面截正方体所得截面面积的最大值为
三、填空题:本题共3小题,每小题5分,共15分.
12.已知数列 是首项为1,公差为2的等差数列,若 ,则 __________.
13.已知圆 ,过点 的直线 交圆 于 两点,且 ,则满足上述条件的一条
直线 的方程为__________.
14.已知函数 ,若在区间 上有且仅有两个不相等的实数 ,满足
,则 的取值范围为__________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)
记 的内角 的对边分别为 ,已知 .
(1)求 ;
(2)若 ,求 的范围.
16.(本小题满分15分)
2020年11月,国务院办公厅印发《新能源汽车产业发展规划(2021—2035年)》,要求深入实施发展新能
源汽车国家战略,推动中国新能源汽车产业高质量可持续发展,加快建设汽车强国.新能源汽车是指采用非常
规的车用燃料作为动力来源(或使用常规的车用燃料、采用新型车载动力装置),综合车辆的动力控制和驱动
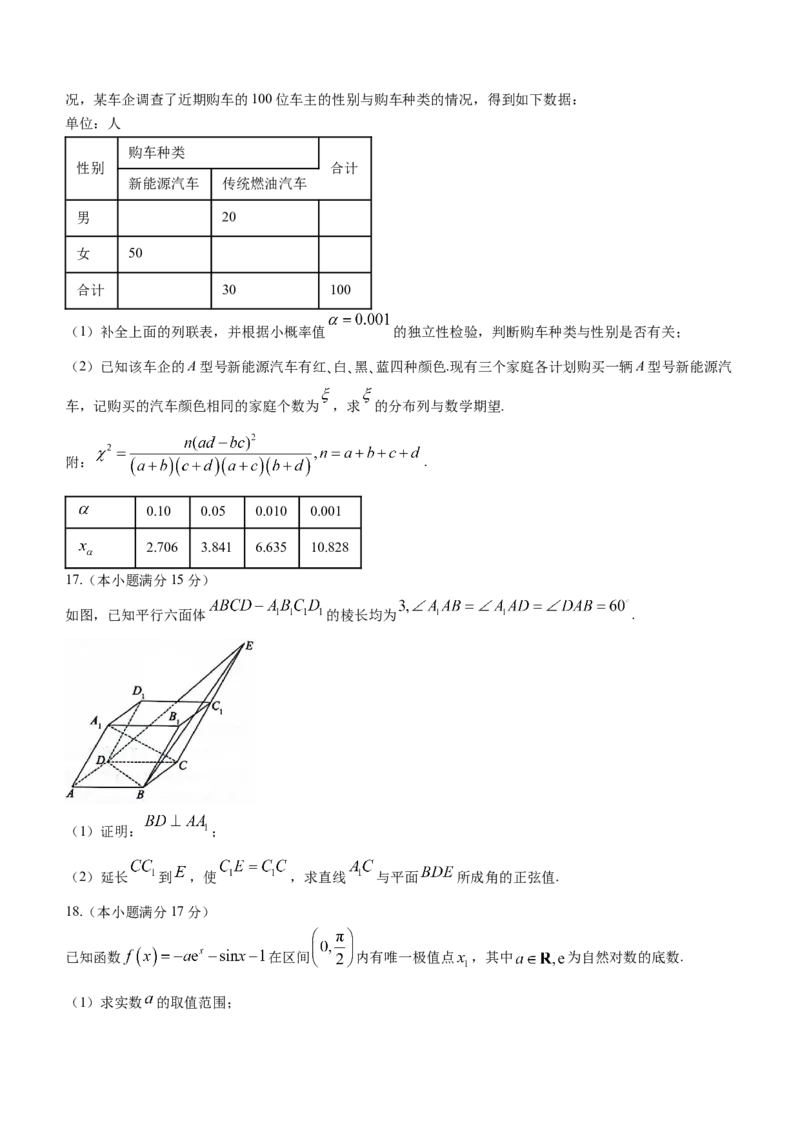
方面的先进技术,形成的技术原理先进、具有新技术、新结构的汽车.为了了解消费者对不同种类汽车的购买情况,某车企调查了近期购车的100位车主的性别与购车种类的情况,得到如下数据:
单位:人
购车种类
性别 合计
新能源汽车 传统燃油汽车
男 20
女 50
合计 30 100
(1)补全上面的列联表,并根据小概率值 的独立性检验,判断购车种类与性别是否有关;
(2)已知该车企的A型号新能源汽车有红、白、黑、蓝四种颜色.现有三个家庭各计划购买一辆A型号新能源汽
车,记购买的汽车颜色相同的家庭个数为 ,求 的分布列与数学期望.
附: .
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
17.(本小题满分15分)
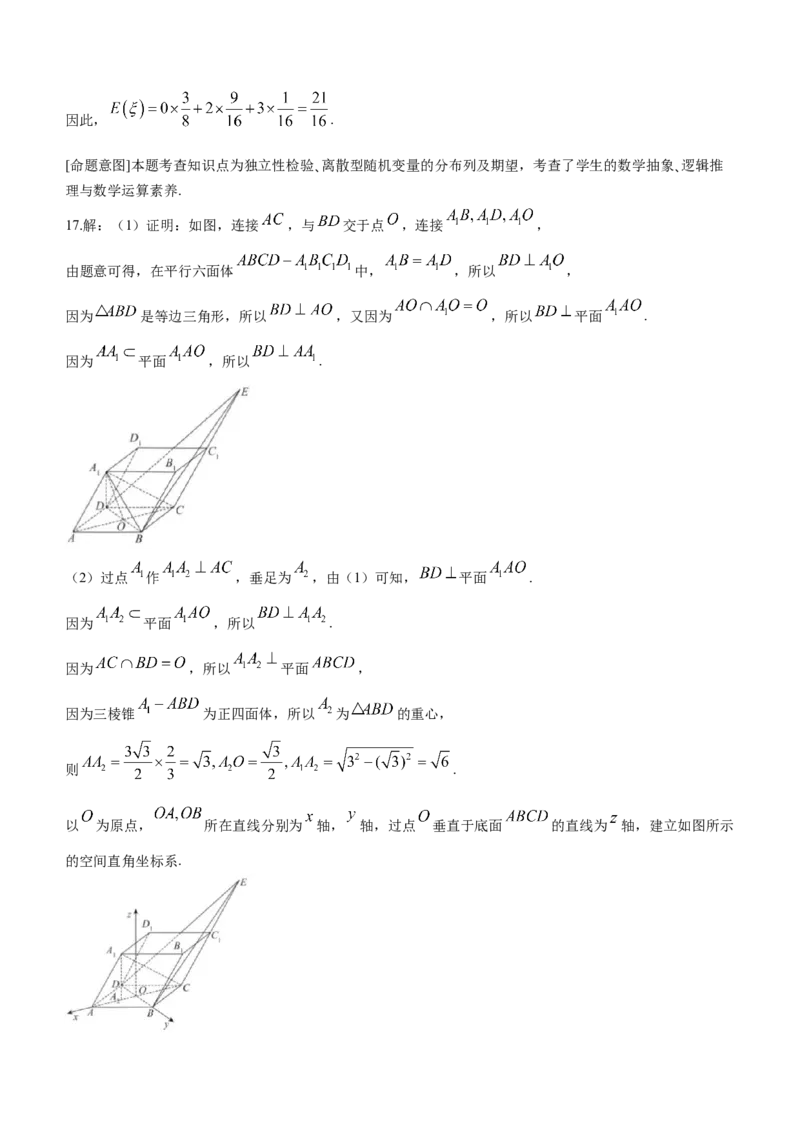
如图,已知平行六面体 的棱长均为 .
(1)证明: ;
(2)延长 到 ,使 ,求直线 与平面 所成角的正弦值.
18.(本小题满分17分)
已知函数 在区间 内有唯一极值点 ,其中 为自然对数的底数.
(1)求实数 的取值范围;(2)证明: 在区间 内有唯一零点.
19.(本小题满分17分)
信息熵是信息论之父香农(Shannon)定义的一个重要概念,香农在1948年发表的论文《通信的数学理论》
中指出,任何信息都存在冗余,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵
的数学表达式:设随机变量 所有可能的取值为 ,且
,定义 的信息熵 .
(1)当 时,计算 ;
(2)若 ,判断并证明当 增大时, 的变化趋势;
(3)若 ,随机变量 所有可能的取值为 ,且
,证明: .2023—2024 高三省级联测考试数学参考答案
题号 1 2 3 4 5 6 7 8 9 10 11
答案 A A B C B C D C ACD CD BCD
1.A 解析:因为 ,又 ,所以 .故选A.
[命题意图]本题考查知识点为集合的运算、解不等式,考查了学生的数学运算素养.
2.A 解析:因为 ,所以 ,所以 .
故选A.
[命题意图]本题考查知识点为复数的运算、共轭复数的概念,考查了学生的数学运算素养.
3.B 解析:因为 ,且 ,所以.故选B.
[命题意图]本题考查知识点为平面向量的线性运算,考查了学生的逻辑推理与数学运算素养.
4.C 解析:因为 ,所以
.故选C.
[命题意图]本题考查知识点为三角函数公式,考查了学生的逻辑推理与数学运算素养.
5.B 解析:过点 作 的垂线,垂足为 ,则 ,设 ,因为 ,所以
,所以 ,所以 .故选B.
[命题意图]本题考查知识点为抛物线的定义,直线的倾斜角,考查了学生的逻辑推理与数学运算素养.
6.C 解析:设 “甲同学报的活动其他同学不报”, “4位同学所报活动各不相同”,由题得
,所以 .故选C.
[命题意图]本题考查知识点为条件概率,考查了学生的数学抽象、逻辑推理与数学运算素养.
7.D 解析:因为 ,所以 ,又 ,所以 ,所以
,在 中, ,在
中, ,因为 ,
所以 ,整理得 ,故 ,故离心率
.故选D.
[命题意图]本题考查知识点为双曲线的离心率,考查了学生的数学抽象、逻辑推理与数学运算素养.8.C 解析:令 ,则 ,令
.当 时, 单调递增,
,所以存在 ,使得 ,且当 时,
单调递减;当 时, 单调递增.又
,所以存在 ,使得 ,且当 时,
单调递增;当 时, , 单调递减.又
,所以当 时, ,即 .当 时,
则 ,即 .令 ,所
以 ,当 时,则 ,即 ,故 .故选C.
[命题意图]本题考查知识点为利用导数比较大小,考查了学生的数学抽象、逻辑推理与数学运算素养.
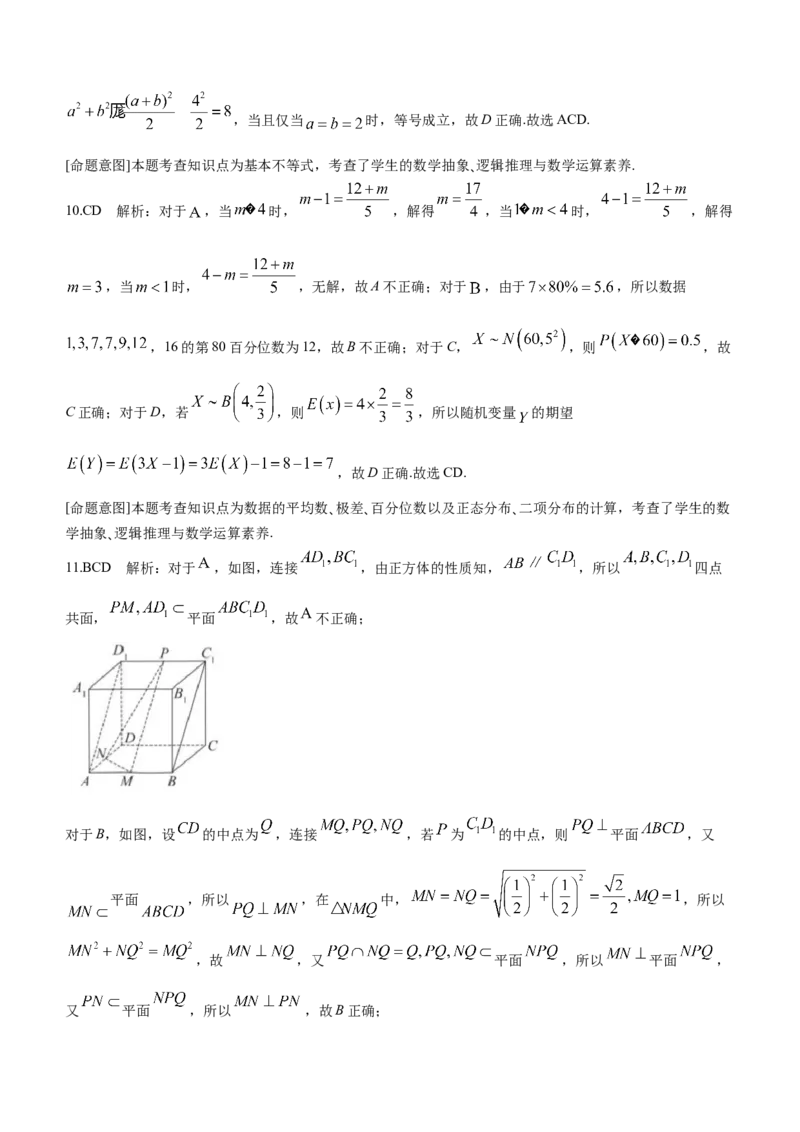
9.ACD 解析:对于 ,由题可得 ,即 ,故A正确;对于
,当且仅当 时,等号成立,故B不正确;对于C,
,当且仅当 时,等号成立,故C正确;对于D,,当且仅当 时,等号成立,故D正确.故选ACD.
[命题意图]本题考查知识点为基本不等式,考查了学生的数学抽象、逻辑推理与数学运算素养.
10.CD 解析:对于 ,当 时, ,解得 ,当 时, ,解得
,当 时, ,无解,故A不正确;对于 ,由于 ,所以数据
,16的第80百分位数为12,故B不正确;对于C, ,则 ,故
C正确;对于D,若 ,则 ,所以随机变量 的期望
,故D正确.故选CD.
[命题意图]本题考查知识点为数据的平均数、极差、百分位数以及正态分布、二项分布的计算,考查了学生的数
学抽象、逻辑推理与数学运算素养.
11.BCD 解析:对于 ,如图,连接 ,由正方体的性质知, ,所以 四点
共面, 平面 ,故 不正确;
对于B,如图,设 的中点为 ,连接 ,若 为 的中点,则 平面 ,又
平面 ,所以 ,在 中, ,所以
,故 ,又 平面 ,所以 平面 ,
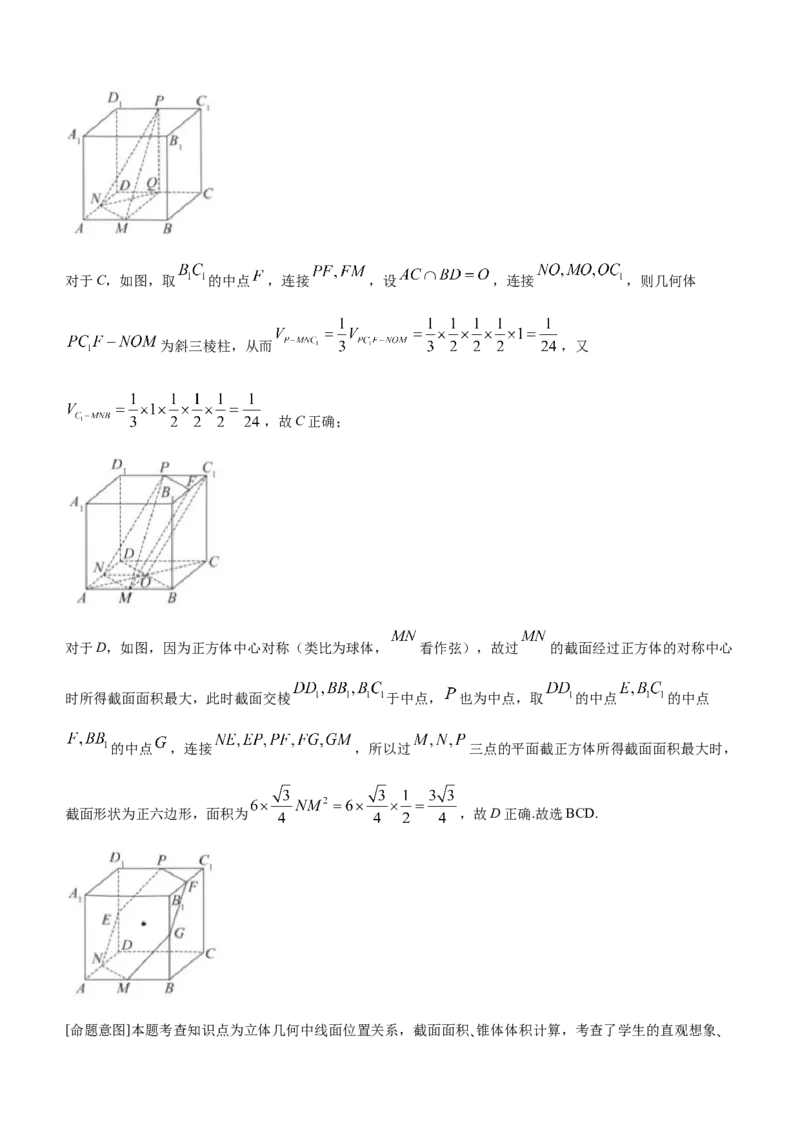
又 平面 ,所以 ,故B正确;对于C,如图,取 的中点 ,连接 ,设 ,连接 ,则几何体
为斜三棱柱,从而 ,又
,故C正确;
对于D,如图,因为正方体中心对称(类比为球体, 看作弦),故过 的截面经过正方体的对称中心
时所得截面面积最大,此时截面交棱 于中点, 也为中点,取 的中点 的中点
的中点 ,连接 ,所以过 三点的平面截正方体所得截面面积最大时,
截面形状为正六边形,面积为 ,故D正确.故选BCD.
[命题意图]本题考查知识点为立体几何中线面位置关系,截面面积、锥体体积计算,考查了学生的直观想象、数学抽象、逻辑推理与数学运算素养.
12.8 解析:由题意得 ,解得 .
[命题意图]本题考查知识点为等差数列的定义,考查了学生的逻辑推理与数学运算素养.
13. (或 ) 解析:由题意得圆心 ,半径 ,故点 在圆
外,设点 到直线 的距离为 ,由 ,得 ,即 ,即
,解得 ,当直线 的斜率不存在时,即 ,此时 ,符合题意;当直线
的斜率存在时,设直线 的方程为 ,则 ,解得 ,故直线 的方程为
.综上,直线 的方程为 或 .
[命题意图]本题考查知识点为直线与圆的位置关系,考查了学生的逻辑推理与数学运算素养.
14. 解析: ,令 ,因为 ,所以
,所以 ,解得 ,故 的取值范围为 .
[命题意图]本题考查知识点为三角函数图象的性质,考查了学生的直观想象、謾辑推理与数学运算素养.
15.解:(1)由正弦定理得, ,
因为 ,所以 ,所以 ,则 ,
因为 ,所以 ,
所以 ,所以 .
(2)因为 ,则 ,因为 .
所以 .
因为 .所以 .所以 ,
所以 .
[命题意图]本题考查知识点为解三角形中的求角和取值范围问题,考查了学生的逻辑推理与数学运算素养.
16.解:(1)
单位:人
购车种类
性别 合计
新能源汽车 传统燃油汽车
男 20 20 40
女 50 10 60
合计 70 30 100
零假设 :购车种类与性别无关,
,
根据小概率值 的独立性检验,我们推断 不成立,即购车种类与性别有关,此推断犯错误的
概率不大于0.001.
(2)由题得 的可能取值为 ,
,
所以 的分布列为
0 2 3因此, .
[命题意图]本题考查知识点为独立性检验、离散型随机变量的分布列及期望,考查了学生的数学抽象、逻辑推
理与数学运算素养.
17.解:(1)证明:如图,连接 ,与 交于点 ,连接 ,
由题意可得,在平行六面体 中, ,所以 ,
因为 是等边三角形,所以 ,又因为 ,所以 平面 .
因为 平面 ,所以 .
(2)过点 作 ,垂足为 ,由(1)可知, 平面 .
因为 平面 ,所以 .
因为 ,所以 平面 ,
因为三棱锥 为正四面体,所以 为 的重心,
则 .
以 为原点, 所在直线分别为 轴, 轴,过点 垂直于底面 的直线为 轴,建立如图所示
的空间直角坐标系.则 ,则 ,
因为 ,所以 ,
所以 ,
所以 ,
设平面 的法向量为 ,
则 所以 令 ,则 ,
设直线 与平面 所成角为 ,
则 ,
所以直线 与平面 所成角的正弦值为 .
[命题意图]本题考查知识点为立体几何中的线面关系和利用空间向量解决空间角,考查了学生的直观想象、逻
辑推理与数学运算素养.
18.解:(1) ,当 时, ,
①当 时, 在 上单调递减,没有极值点,不合题意;
②当 时, 与 在 上分别单调递增,显然 在 上单调递增,
因为 ,
所以 ,得 ,此时 在 内有唯一零点 ,所以当 时, ;当 时, ,
所以 在 内有唯一极小值点 ,符合题意.
综上,实数 的取值范围为 .
(2)证明:由(1)知 ,所以当 时, ,
所以当 时, 单调递减;当 时, 单调递增,
所以当 时, ,则 ,
又因为 ,所以 在 内有唯一零点,
即 在 内有唯一零点.
[命题意图]本题考查知识点为导数与极值点、零点,考查了学生的数学抽象、逻辑推理与数学运算素养.
19.解:(1)当 时,则 ,所以 .
(2) 随着 的增大而增大.
当 ,则 ,
设 ,则 ,
因此 随着 的增大而增大.
(3)证明:若 ,随机变量 所有可能的取值为 ,且
.
..
.
由于 ,所以 ,所以 ,
所以 ,
所以 .
[命题意图]本题考查知识点为对新定义“信息熵”的理解和运用,考查分析、思考和解决问题的能力,涉及对
数运算和对数函数及不等式的基本性质的运用,考查学生的逻辑推理能力和数学运算素养.