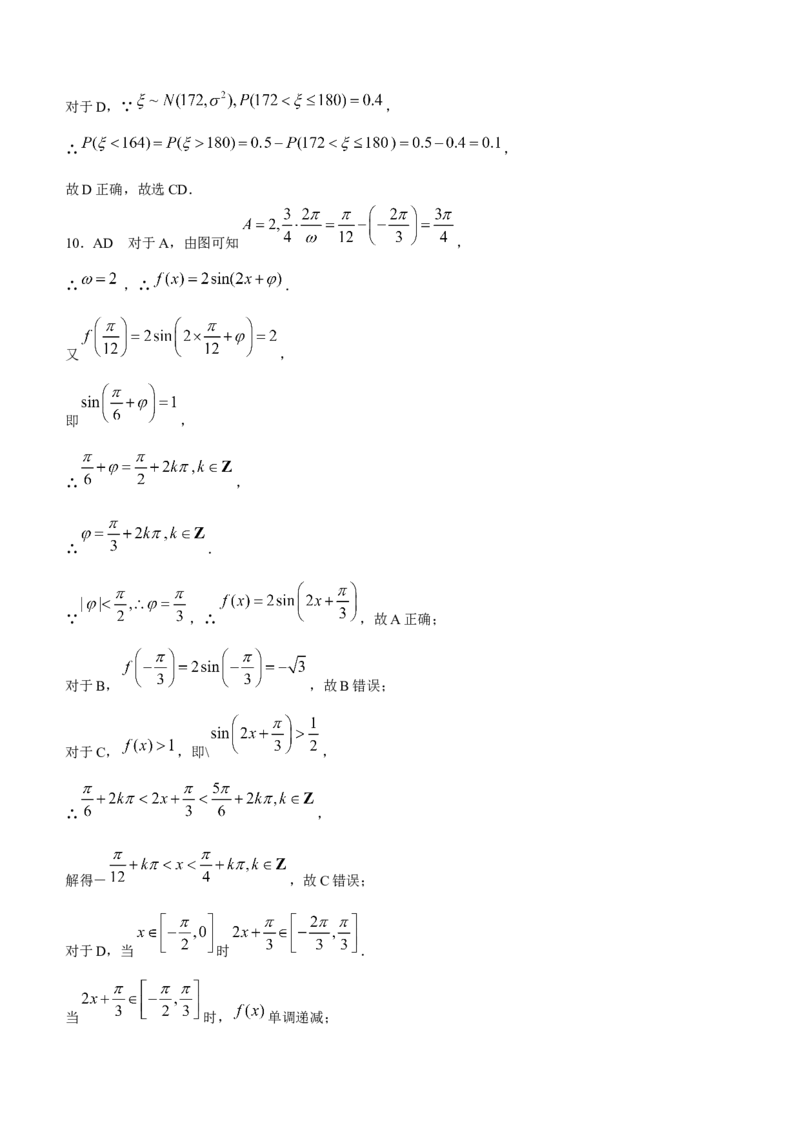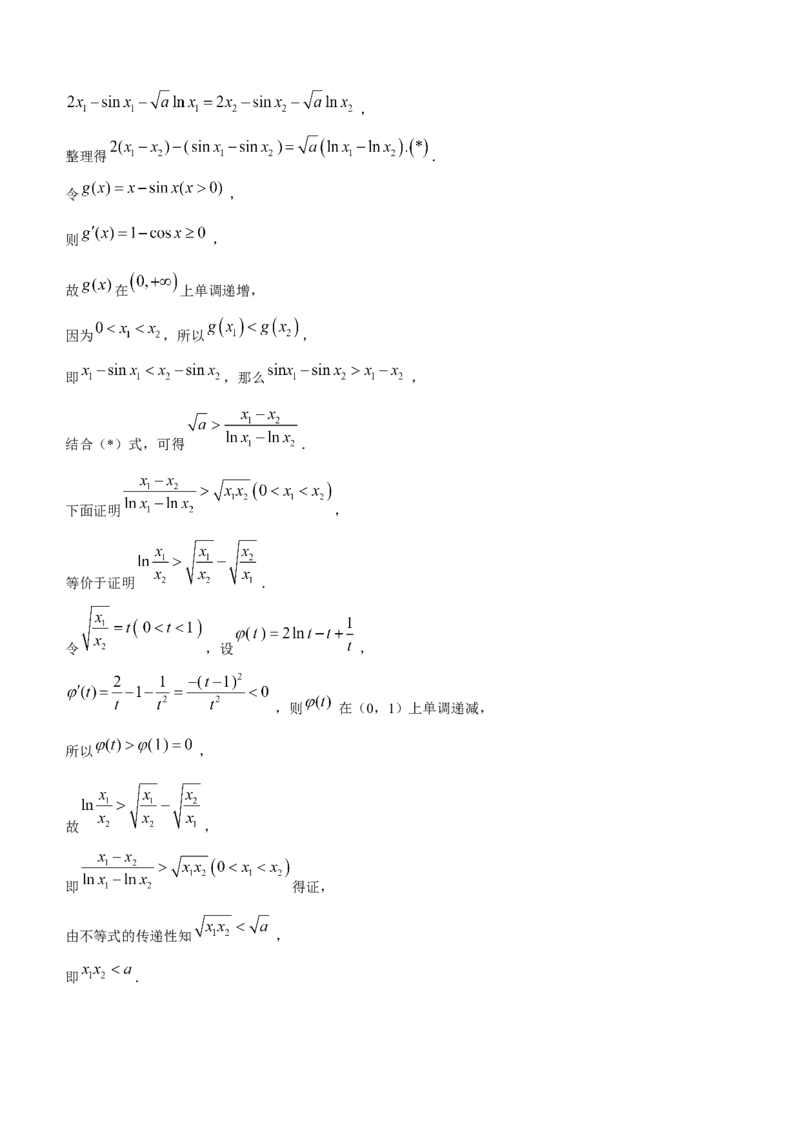文档内容
2023-2024 学年海南省高考全真模拟卷(六)
数学
1.本试卷满分150分,测试时间120分钟,共4页.
2.考查范围:高考全部内容.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的)
1.已知复数 满足 ,则z的共轭复数 在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知集合 , ,若 中恰有两个元素,则实数m
的取值范围为( )
A.(-1,0) B.(0,1) C.[0,1] D.R
3.已知 ,则“ ”是“ 的二项展开式中常数项为60”的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
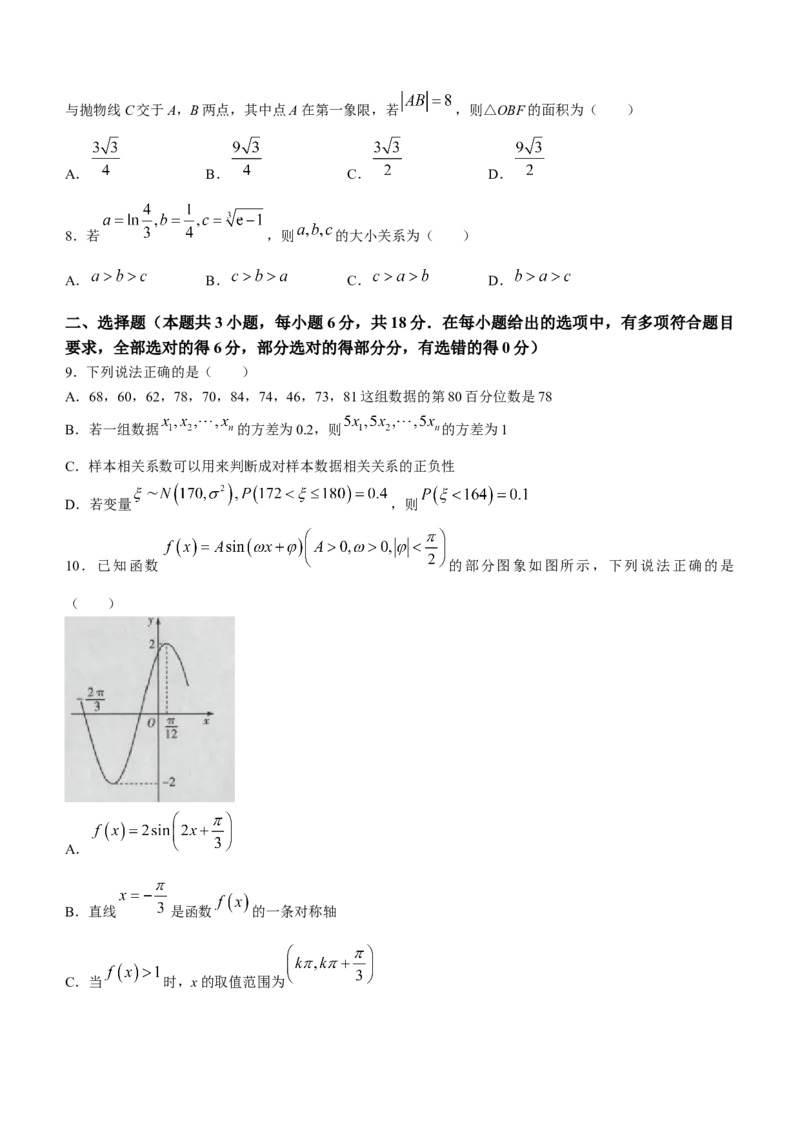
4.如图,点P,A,B均在边长为1的小正方形组成的网格上,则 ( )
A.-8 B.-4 C.0 D.4
5.等差数列 的前n项和为 ,已知 ,则 的前100项中, 为整数的各项之和为
( )
A.1089 B.1099 C.1156 D.1166
6.在一次立体几何模型的实践课上,老师要求学生将边长为4的正方形ABCD沿对角线AC进行翻折,使得
D到达 的位置,此时平面 平面BAC,连接 ,得到四面体 ,记四面体 的外接
球球心为O,则点O到平面 的距离为( )
A. B. C. D.
7.在平面直角坐标系xOy中,已知抛物线 的焦点为F,过点F且倾斜角为120°的直线与抛物线C交于A,B两点,其中点A在第一象限,若 ,则△OBF的面积为( )
A. B. C. D.
8.若 ,则 的大小关系为( )
A. B. C. D.
二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.下列说法正确的是( )
A.68,60,62,78,70,84,74,46,73,81这组数据的第80百分位数是78
B.若一组数据 的方差为0.2,则 的方差为1
C.样本相关系数可以用来判断成对样本数据相关关系的正负性
D.若变量 ,则
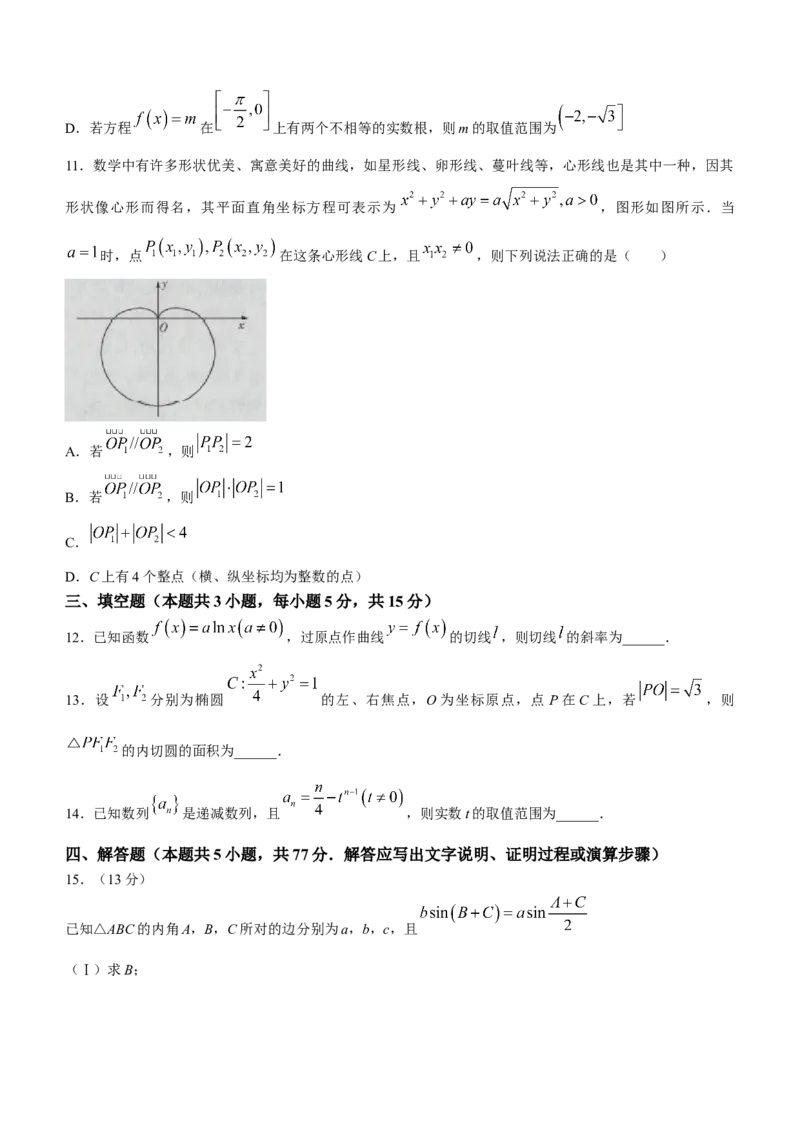
10.已知函数 的部分图象如图所示,下列说法正确的是
( )
A.
B.直线 是函数 的一条对称轴
C.当 时,x的取值范围为D.若方程 在 上有两个不相等的实数根,则m的取值范围为
11.数学中有许多形状优美、寓意美好的曲线,如星形线、卵形线、蔓叶线等,心形线也是其中一种,因其
形状像心形而得名,其平面直角坐标方程可表示为 ,图形如图所示.当
时,点 在这条心形线C上,且 ,则下列说法正确的是( )
A.若 ,则
B.若 ,则
C.
D.C上有4个整点(横、纵坐标均为整数的点)
三、填空题(本题共3小题,每小题5分,共15分)
12.已知函数 ,过原点作曲线 的切线 ,则切线 的斜率为______.
13.设 分别为椭圆 的左、右焦点,O为坐标原点,点 P在C上,若 ,则
的内切圆的面积为______.
14.已知数列 是递减数列,且 ,则实数t的取值范围为______.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)
已知△ABC的内角A,B,C所对的边分别为a,b,c,且
(Ⅰ)求B;(Ⅱ)若点D在AC上,且AD=BD=2DC,求 .
16.(15分)
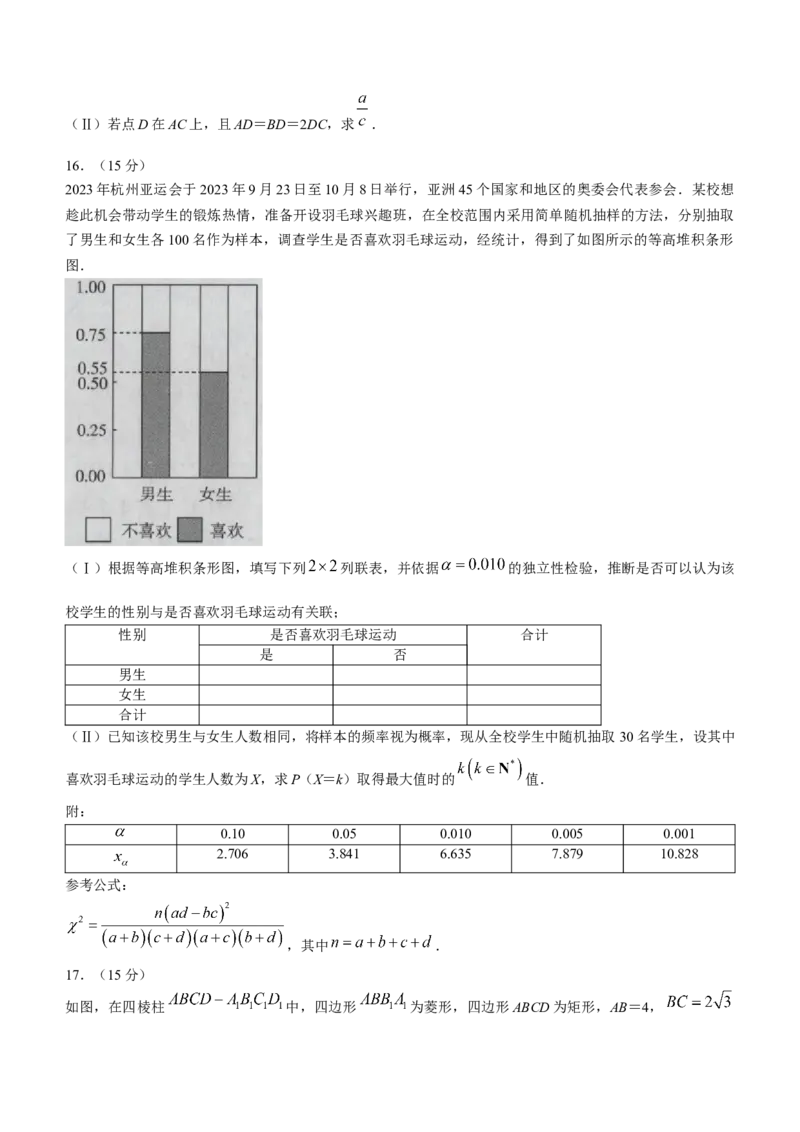
2023年杭州亚运会于2023年9月23日至10月8日举行,亚洲45个国家和地区的奥委会代表参会.某校想
趁此机会带动学生的锻炼热情,准备开设羽毛球兴趣班,在全校范围内采用简单随机抽样的方法,分别抽取
了男生和女生各100名作为样本,调查学生是否喜欢羽毛球运动,经统计,得到了如图所示的等高堆积条形
图.
(Ⅰ)根据等高堆积条形图,填写下列 列联表,并依据 的独立性检验,推断是否可以认为该
校学生的性别与是否喜欢羽毛球运动有关联;
性别 是否喜欢羽毛球运动 合计
是 否
男生
女生
合计
(Ⅱ)已知该校男生与女生人数相同,将样本的频率视为概率,现从全校学生中随机抽取 30名学生,设其中
喜欢羽毛球运动的学生人数为X,求P(X=k)取得最大值时的 值.
附:
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:
,其中 .
17.(15分)
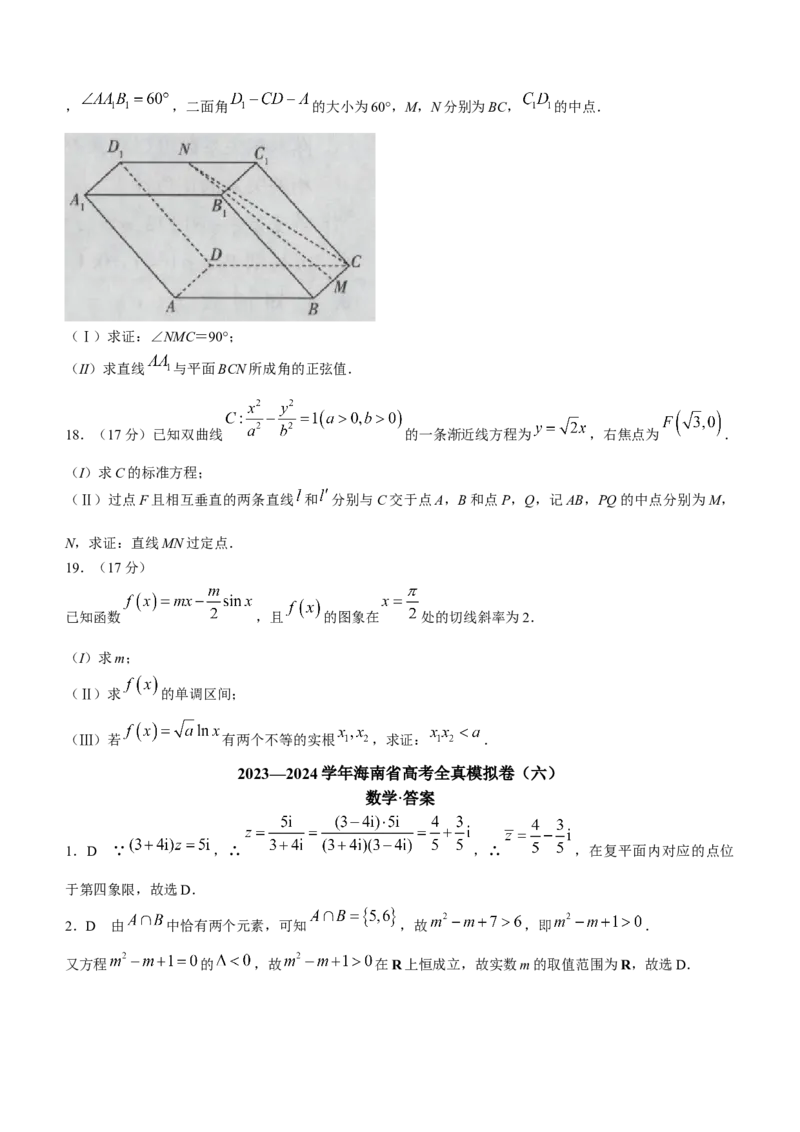
如图,在四棱柱 中,四边形 为菱形,四边形ABCD为矩形,AB=4,, ,二面角 的大小为60°,M,N分别为BC, 的中点.
(Ⅰ)求证:∠NMC=90°;
(II)求直线 与平面BCN所成角的正弦值.
18.(17分)已知双曲线 的一条渐近线方程为 ,右焦点为 .
(I)求C的标准方程;
(Ⅱ)过点F且相互垂直的两条直线 和 分别与C交于点A,B和点P,Q,记AB,PQ的中点分别为M,
N,求证:直线MN过定点.
19.(17分)
已知函数 ,且 的图象在 处的切线斜率为2.
(I)求m;
(Ⅱ)求 的单调区间;
(Ⅲ)若 有两个不等的实根 ,求证: .
2023—2024学年海南省高考全真模拟卷(六)
数学·答案
1.D ∵ ,∴ ,∴ ,在复平面内对应的点位
于第四象限,故选D.
2.D 由 中恰有两个元素,可知 ,故 ,即 .
又方程 的 ,故 在R上恒成立,故实数m的取值范围为R,故选D.3.B 的展开式的通项为 .
令 ,得 ,则 的常数项为 .
∴当 时,常数项为60;
当常数项为60时, ,
∴“ ”是“ 的二项展开式中常数项为60”的充分不必要条件,故选B.
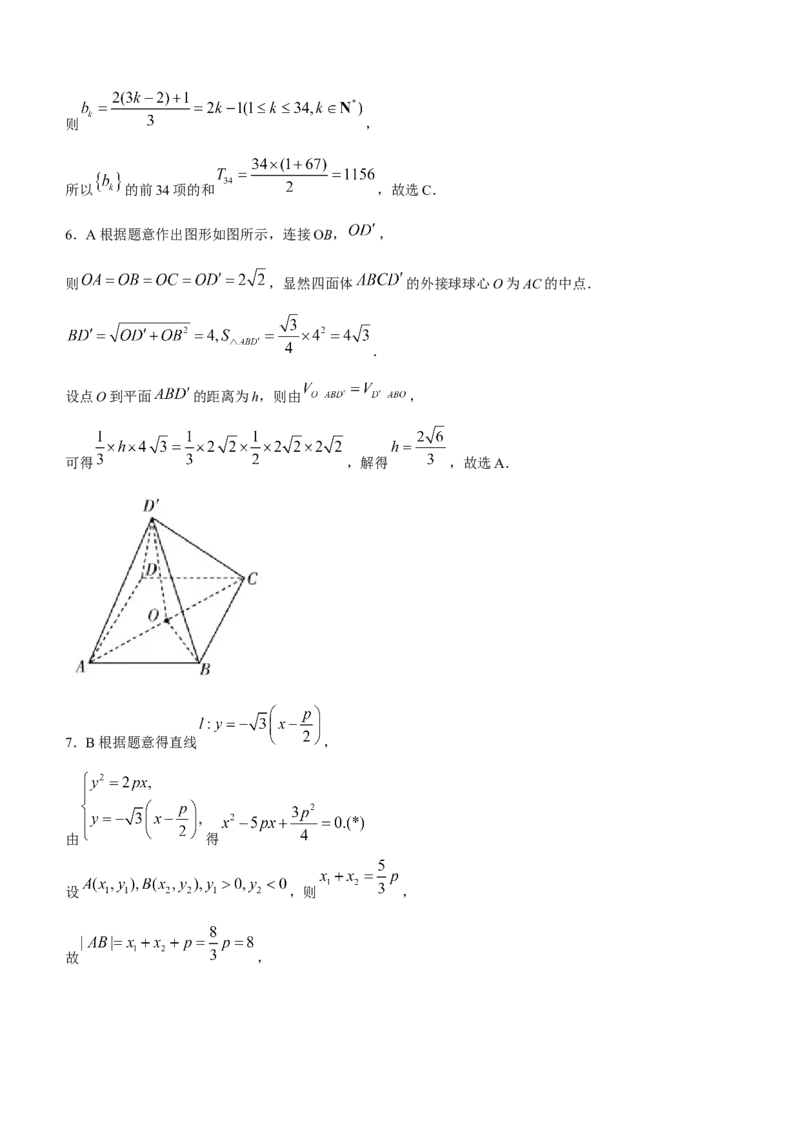
4.A 如图,以点P为坐标原点,建立平面直角坐标系,则 :,
,
,故选A.
5.C 设等差数列 的公差为d,
由 , 解得 ,
所以 .
要使 为整数,则 是3的倍数,又 ,
所以可令 .
记 的前100项中的整数项构成的数列为 ,则 ,
所以 的前34项的和 ,故选C.
6.A根据题意作出图形如图所示,连接OB, ,
则 ,显然四面体 的外接球球心O为AC的中点.
.
设点O到平面 的距离为h,则由 ,
可得 ,解得 ,故选A.
7.B根据题意得直线 ,
由 得
设 ,则 ,
故 ,解得 ,代入(*)式,解得 .
将 代入直线 的方程中,
解得 ,故 ,故选B.
8.C设 ,
则 ,
∴ 时, , 在 上单调递增.
∴ ,即 ,
∴ , .
设 :,则 ,
∴当 时, ,即 在 上单调递增.
∴ , ,∴ ,即 .
综上, 故选C.
9.CD 对于A,这组数据从小到大排列为:46,60,62,68,70,73,74,78,81,又 ,
第8位数字是78,第9位数字是81,故这组数据的第80百分位数是 ,故A错误;
对于B, 的方差为 ,故B错误;
对于C,样本相关系数r的符号反映了相关关系的正负性,当 时,成对样本数据正相关,当 时,
成对样本数据负相关,故C正确;对于D,∵ ,
∴ ,
故D正确,故选CD.
10.AD 对于A,由图可知 ,
∴ ,∴ .
又 ,
即 ,
∴ ,
∴ .
∵ ,∴ ,故A正确;
对于B, ,故B错误;
对于C, ,即\ ,
∴ ,
解得- ,故C错误;
对于D,当 时 .
当 时, 单调递减;当 时, 单调递增.
∵ , , ,
∴要使方程 在 上有两个不相等的实数根,
则 ,故D正确,故选AD.
11.ACD 依题意,心形线C的直角坐标方程为 ,过原点 .
由 ,可知 三点共线,
可设直线 ,由
消去y,得 .
不妨设 ,
则 .
∴ ,故A正确;
,
当 时, ,故B错误;
设点 在心形线C上, ,角 以x轴非负半轴为起始边,
则心形线C的方程转化为 ,
即 ,
∴ ,又 ,∴ ,故C正确;
由 ,可知 .
令 ,则心形线C的方程可
化为 :,
∴ ,当 ,得 或0,
当 时,方程无整数解;
当 时,
∴C上有4个整点(-1,0),(1,0),(0,0),(0,-2),故D正确,故选ACD.
12. 根据题意得, .设切点坐标为 ,则 ,
所以切线 的方程为 ,
将点(0,0)代入,可得 ,
整理得 ,故 ,解得 ,
故 ,即切线 的斜率为 .
13. 不妨设 , ,则 .
在 中,由余弦定理得, .
由 ,且 ,
可得 ,
即 ,所以 ,
所以内切圆半径为 ,
所以 的内切圆的面积为 .
14. ∵数列 是递减数列,
∴ ,即 ,
化简得 .
当 时, 的值有正有负,
∴ 不恒成立;
当 时, , ,
∴ 不成立;
当 时,
由题意得, ,
∵当 时, 取得最小值,
即有 ,解得 ,
∴实数t的取值范围为 .
15.解:(I)∵ ,
∴ ,∴ ,
由正弦定理得, ,
即 ,
故 .
∵ ,
∴ ,∴ ,
故 .
(Ⅱ)∵ ,∴ ,
∴ ,即 ,
整理得 ,
∴ ,
即 ,∴ .
16.解:(I)由题意,完成 列联表如下:
性别 是否喜欢羽毛球运动 合计
是 否
男生 75 25 100
女生 55 45 100合计 130 70 200
零假设为
:该校学生的性别与是否喜欢羽毛球运动没有关联.
,
∴依据小概率值 的独立性检验,
我们推断 不成立,即能认为该校学生喜欢羽毛球运动与性别有关联.
(Ⅱ)由列联表可知,该校学生喜欢羽毛球运动的频率为 ,
∴随机变量 ,
∴ .
要使 取得最大值,
则需
解得 ,
∵ ,
∴当 时, 取得最大值.
17.解:(I)取AD的中点O,连接OM,ON,AN,DN.
在菱形 中,易知 ,且
又 ,故 即为二面角 的平面角,
故 .所以 为等边三角形,所以 .
显然 ,且 ,
所以 平面MON
又 平面MON,所以 ,
又 ,所以 ,
故 .
(Ⅱ)由(I)可知, 平面ADN.
又 平面ABCD,,
所以平面 平面ABCD.
又平面 平面 , 平面ADN,且 ,
故 平面ABCD,故OA,OM,ON两两相互垂直.
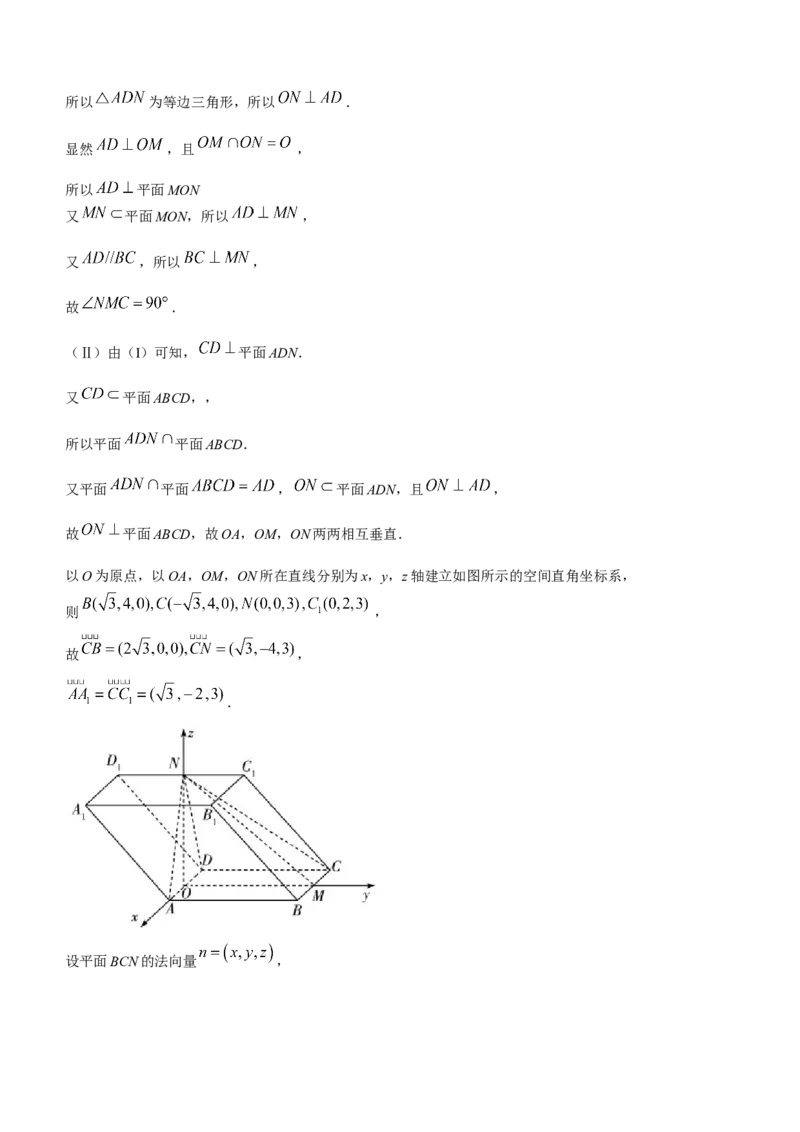
以O为原点,以OA,OM,ON所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则 ,
故 ,
.
设平面BCN的法向量 ,则. ,
取 ,则 .
记直线 与平面BCN所成角为 ,
则 ,
故直线 与平面BCN所成角的正弦值为 .
18.解:(I)设双曲线C的半焦距为c,根据题意
得 解得
∴C的标准方程为 .
(II)当直线 和 斜率均存在时,
设直线 的方程为 , , ,中点
由 消去 ,得 .
∴ , .
∴ .
设直线 的方程为 ,
,中点 .同理可得 .
∵ ,∴ , .
当 时, ,此时 ,直线MN的方程为
当 时, ,此时直线MN的斜率 ,
直线MN的方程为 ,
即 .
此时直线MN过定点 .
当直线 和 其中一条直线的斜率不存在时,易知MN所在直线为x轴.
综上所述,直线MN过定点 .
19.解:(I)因为 ,
所以 ,
根据题意得 ,
解得 .
(II)由(I)可知 ,
,又 ,
所以 ,故 的单调递增区间为R,无单调递减区间
(Ш)由 有两个不等的根 (不妨设 ),可得,
整理得 .
令 ,
则 ,
故 在 上单调递增,
因为 ,所以 ,
即 ,那么 ,
结合(*)式,可得 .
下面证明 ,
等价于证明 .
令 ,设 ,
,则 在(0,1)上单调递减,
所以 ,
故 ,
即 得证,
由不等式的传递性知 ,
即 .