文档内容
数学试题参考答案及评分标准
一!选择题"本题共"小题#每小题#分#共$%分&在每小题给出的四个选项中#只有一个选项符
合题目要求&
!!#命题意图$考查复数的基本运算及复数模长的计算%考查数学运算素养%命题设计体现基
础性!
#思路点拨$由条件化简得到"的表达式%再代入模长的计算公式求解!
#答案$’
" ! ")( ( (
#详细过程$因为 * %所以 *()+%所以 *!)+%所以"* *!,+%所以"""*
()" ()+ " " !)+
槡(%故正确选项为’&
(!#命题意图$考查集合的含义与表示以及集合的基本运算%考查绝对值不等式的解法和初等函
数的值域%考查表示集合的符号语言与图形语言间的转化%命题设计体现基础性!
#思路点拨$由条件求出集合#和集合$%再结合图形%根据集合的交集&并集和补集运算求出
答案!
#答案$-
#详细过程$由"%"#!得,!#%#!%所以#*’,!%!(%函数&*槡%,!的值域为’%%)."%所
以$*’%%)."!图中阴影部分表示的集合为$ !#%$"%因为#%$*’,!%)."%所以
!
$ !#%$"*!,.%,!"%故正确选项为-&
!
/!#命题意图$考查根据椭圆的标准方程判断焦点的位置以及椭圆离心率的求解%考查分类讨论
思想的应用%命题设计体现基础性和创新性!
#思路点拨$根据椭圆的方程分类讨论建立’与(的关系式%进而求得答案!
#答案$-
#详细过程$由题意’&%%(&%且’’(!设椭圆的长半轴长为)%短半轴长为*%半焦距为+%离
/ ’,( ( !
心率为,!当’&(时%)(*’%*(*(%+(*’,(%则,(* * %解得 * )当’((时%
$ ’ ’ $
/ (,’ ( ( ! (
)(*(%*(*’%+(*(,’%则,(* * %解得 *$!所以 * 或 *$!故正确选项为-&
$ ( ’ ’ $ ’
$!#命题意图$考查条件概率和独立事件的概率乘法公式%考查数学运算和数据分析素养%命题设
计体现基础性和应用性!
#思路点拨$根据条件概率的定义%可知小明只需答对$%-%.%/四道试题中至少三道试题即
可通过测试%因此利用相互独立事件的概率乘法公式即可解答!
#答案$0
#详细过程$因为小明已经答错了试题#%要通过测试只需要答对$%-%.%/四道试题中至少
数学答案 第!!!!!页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}
书书书( ( ! ! ! ( ! ! $
三道试题!所以小明通过测试的概率0*/1 1 1 1 )(1 1 1 1 * %故正
/ / ( ( / / ( ( 2
确选项为0&
#!#命题意图$考查函数极值点的概念%考查函数的奇偶性和单调性的综合%考查复合函数的求导
法则%考查直观想象和逻辑推理素养%命题体现基础性和创新性!
#思路点拨$根据极小值点的概念%可知在% 左右两侧附近导数先负后正%再结合函数的奇偶
%
性可对选项逐一判断!
#答案$0
#详细过程$由题知%存在!&%使得当%)!%,!%%"时%12!%"(%%当%)!%%%)!"时%
% % % %
12!%"&%!对于3选项%因为1!%"为奇函数%则12!%"为偶函数!则当%)!,%%,%)!"时%
% %
12!%"(%%当%)!,%,!%,%"时%12!%"&%%所以,% 是1!%"的极大值点%选项3正确)对
% % %
于’选项%因为&2*12!%"41!%"%显然% 是函数&*41!%"的极小值点%选项’正确)对于-选项%
%
因为&2*,12!,%"41!,%"*,12!%"41!,%"%由选项3知%,% 是函数&*41!,%"的极小值点%
%
-选项正确)对于0选项%因为&2*,12!,%"*,12!%"%显然% 是函数&*1!,%"的极大值
%
点%0选项错误%故正确选项为0&
5!#命题意图$考查三角函数的图象与性质%考查三角函数图象的变换!考查转化与化归思想和数
形结合思想的应用%考查直观想象&逻辑推理和数学运算素养%命题设计体现基础性和创新性!
! !
#思路点拨$思路!*整体思想%令
(
%
%
)"*
/
)(3!%3)"%可求得%
%
%进而可求得结果)
!! "! !"
思路(*将函数1!%"*6+7%的图象经过平移和伸缩变换得到4!%"*6+7 %)" """(
( (
的图象%从而点#逐步变换到#2!%%&"%从中建立关系求解!
% %
#答案$3
! ! (!
#详细过程$解法!*令
(
%
%
)"*
/
)(3!%3)"%所以%
%
*
/
,(")$3!!因为6+7%
%
*
!(! " !(! " ! ! ! ! (! #!
6+7 ,(")$3! *6+7 ,(" * !因为, ("( %所以, ( ,("( %所以
/ / ( ( ( / / /
(! ! (! #! ! ! !
,("* 或 ,("* %解得 "* 或 "*, %所以 " 的所有可能值之和为 %故正确选
/ 5 / 5 $ !( 5
项为3&
解法(*将1!%"*6+7%的图象平移"""个单位得到函数&*6+7!%)" "的图象%则点#的横坐
!
标变为 ," %再将函数&*6+7!%)" "的图象保持纵坐标不变%横坐标伸长为原来的两倍得到
/
!! "! !" (! (!
4!%"*6+7
(
%)" """(
(
的图象%则点#的横坐标变为
/
,(" %所以%
%
*
/
,(" %所以
!(! " ! ! ! ! (! #! (! !
6+7%
%
*6+7
/
,(" *
(
%因为,
(
("(
(
%所以,
/
(
/
,("(
/
%所以
/
,("*
5
或
(! #! ! ! !
,("* %解得 "* 或 "*, %所以 " 的所有可能值之和为 %故正确选项为3&
/ 5 $ !( 5
数学答案 第!!!!(页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}8!#命题意图$考查分段函数最值的理解和求解%结合充分必要条件进行考查%考查直观想象和数
学运算素养%命题体现综合性和创新性!
#思路点拨$对参数)分类讨论%根据)的不同范围判断1!%"的最小值是否存在%再根据充分
必要条件的判断求解!
#答案$-
#详细过程$若)(%%当%&!时%1!%"单调递减%%*).时%1!%"*,.%所以1!%"无最小
值!若)*%%则1!%"在!,.%%"上单调递减%在!%%!"上单调递增%此时1!%"+1!%"*,(%又
!
%&!时%1!%"* )(&(%所以1!%"存在最小值!若%()(!%1!%"在!,.%)"上单调递减%
%
! " ! "
! !
!)%!"上单调递增%在 !%槡 上单调递减%在 槡%). 上单调递增%所以1!%"在%*)
) )
!
处%或%*槡处取得最小值%即1!%"存在最小值!若)+!%则1!%"在!,.%!"上单调递减%
)
在!!%)."上单调递增%要使1!%"存在最小值%需!!,)"(,(#))/%解得,!#)#$%所以
!#)#$!综上所述%+%#)#$,是+1!%"存在最小值,的充要条件!故正确选项为-&
"!#命题意图$考查三角恒等变换%考查逻辑推理和数学运算素养%命题设计体现综合性和应
用性!
!
#思路点拨$首先令 #*$) %代入后化简得到 # 的三角函数值%进而求得结果!当然也可以从
5
条件出发将条件逐项展开再逐步变换求解!
#答案$-
! ! ! !" ! !" ! !"
#详细过程$令 #*$) %即$*#, %则(9:7 ($, )9:7$) *(9:7 (#, )9:7#
5 5 5 5 (
* ,(;<6(# ) 6+7# * ,(;<6(#)(6+7( # * (!/6+7( #,!" *%%所以6+7( #* ! %因为%($( ! %所
6+7(# ;<6# 6+7(# 6+7(# / (
! (! 槡/ 槡/ ! ! 槡5 ! !"
以 (#( %所以6+7#* ( %所以 (#( %所以;<6#* %所以6+7$, *,;<6#
5 / / ( 5 / / /
槡5
*, !故正确选项为-&
/
二!选择题"本题共/小题#每小题5分#共!"分!在每小题给出的四个选项中#有多项符合题目
要求!全部选对的得5分#部分选对的得部分分#有选错的得%分!
2!#命题意图$考查成对数据的分析%考查利用最小二乘法求解经验回归直线方程%考查数据分析
素养%命题设计体现基础性!
#思路点拨$首先根据经验回归直线经过样本的中心%求得5 *%再根据5 *的正负判断&与%成正
相关%再运用经验回归直线方程作预测%最后判断样本相关系数和决定系数间的关系!
#答案$3’0
!)()/)$)#
#详 细 过 程$对 于 3 选 项%由 表 格 中 的 数 据 得 %, * */%& - *
#
数学答案 第!!!!/页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}(=$)/=!)$)#)#=# *$%因为经验回归直线过样本的中心%所以$*/ 5 *)!=#8%解得5 **
#
%="!%所以3选项正确)对于’选项%由选项3知%&与%成正相关关系%所以6&%%所以’选
项正确)对于-选项%由经验回归直线的含义%当%增加!时%&不一定增加%="!%所以-选项
#
错误&对于0选项%因为.!%9%,"!&9& -"89(:!9!=5";!9!":!9%=2";!;(:!=#
7 7
78!
# #
8"=!%.!%9%,"( 8$;!;!;$8!%%.!&9& -"(8 !!=5"(;!%=2"(;!;!!=#"(8
7 7
78! 78!
(
.!%9%,"!&9& -"
7 7 #
5=5(%所以68 78! 8 "=! %6(8 5#5! %.!&9 5 &"(8!%=%("(;
槡. ( !%
7
9%,"(. ( !&
7
9& -"( 槡55=( 55(% 78! 7 7
78! 78!
%=%#2 5#5!
!%=%2"(;!%=!2"(;!%=!("(8%=%#2%则<(8!9 8 %所以6(*<(!注*一般地%
5=5( 55(%
在用最小二乘法求解的线性回归模型中均有6(*<("%所以选项 0正确&综上%正确选项
为3’0&
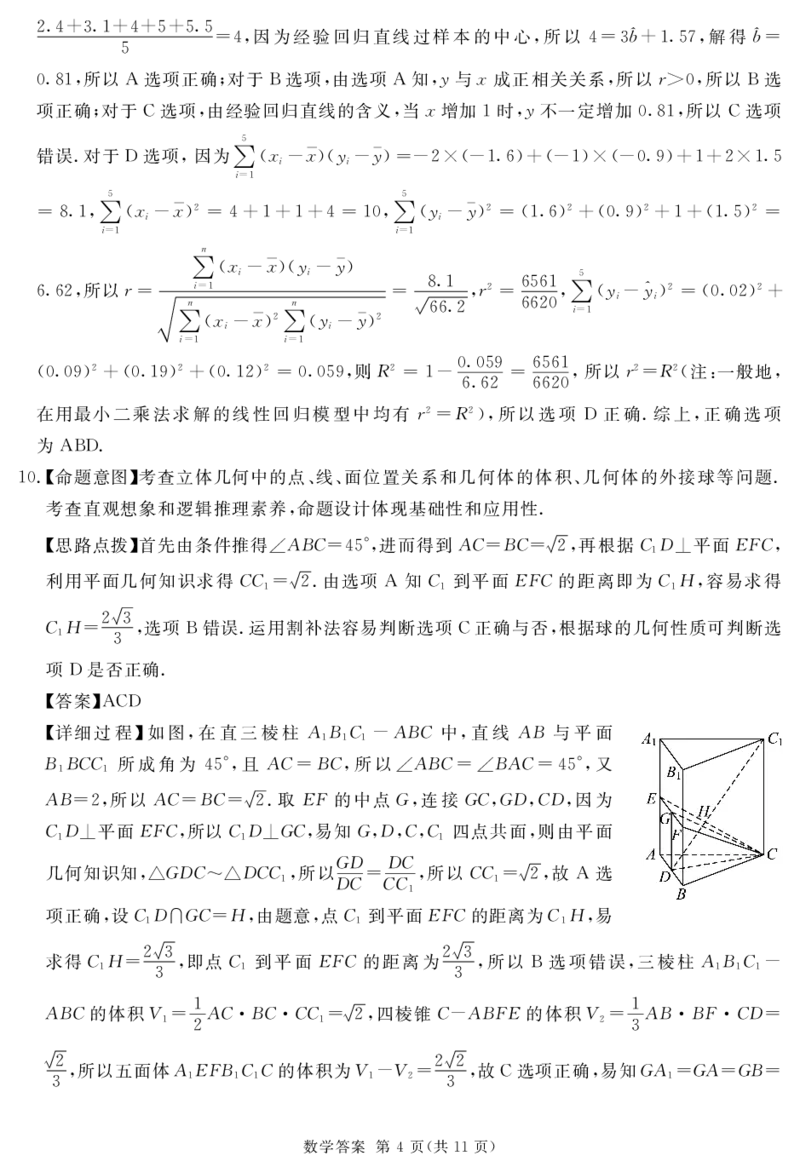
!%!#命题意图$考查立体几何中的点&线&面位置关系和几何体的体积&几何体的外接球等问题!
考查直观想象和逻辑推理素养%命题设计体现基础性和应用性!
#思路点拨$首先由条件推得/#$-*$#>%进而得到#-*$-*槡(%再根据-.0平面/=-%
!
利用平面几何知识求得--*槡(!由选项3知- 到平面/=-的距离即为->%容易求得
! ! !
(槡/
->* %选项’错误!运用割补法容易判断选项-正确与否%根据球的几何性质可判断选
! /
项0是否正确!
#答案$3-0
#详细过程$如图%在直三棱柱#$- ,#$-中%直线#$与平面
! ! !
$$-- 所成角为$#>%且#-*$-%所以/#$-*/$#-*$#>%又
! !
#$*(%所以#-*$-*槡(!取/=的中点?%连接?-%?.%-.%因为
-.0平面/=-%所以-.0?-%易知?%.%-%- 四点共面%则由平面
! ! !
?. .-
几何知识知%1?.-"1.--%所以 * %所以--*槡(%故3选
! .- -- !
!
项正确%设-.2?-*>%由题意%点- 到平面/=-的距离为->%易
! ! !
(槡/ (槡/
求得->* %即点- 到平面/=-的距离为 %所以’选项错误%三棱柱#$- ,
! / ! / ! ! !
! !
#$-的体积@ * #--$----*槡(%四棱锥-,#$=/的体积@ * #$-$=--.*
! ( ! ( /
槡( (槡(
%所以五面体#/=$--的体积为@ ,@ * %故-选项正确%易知?#*?#*?$*
/ ! ! ! ! ( / !
数学答案 第!!!!$页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}槡5 槡5
?$*?-*?-* %所以三棱柱#$-,#$-的外接球的球心为?%半径为 %故其表面
! ! ( ! ! ! (
积为5!%所以0选项正确%综上所述%正确选项为3-0&
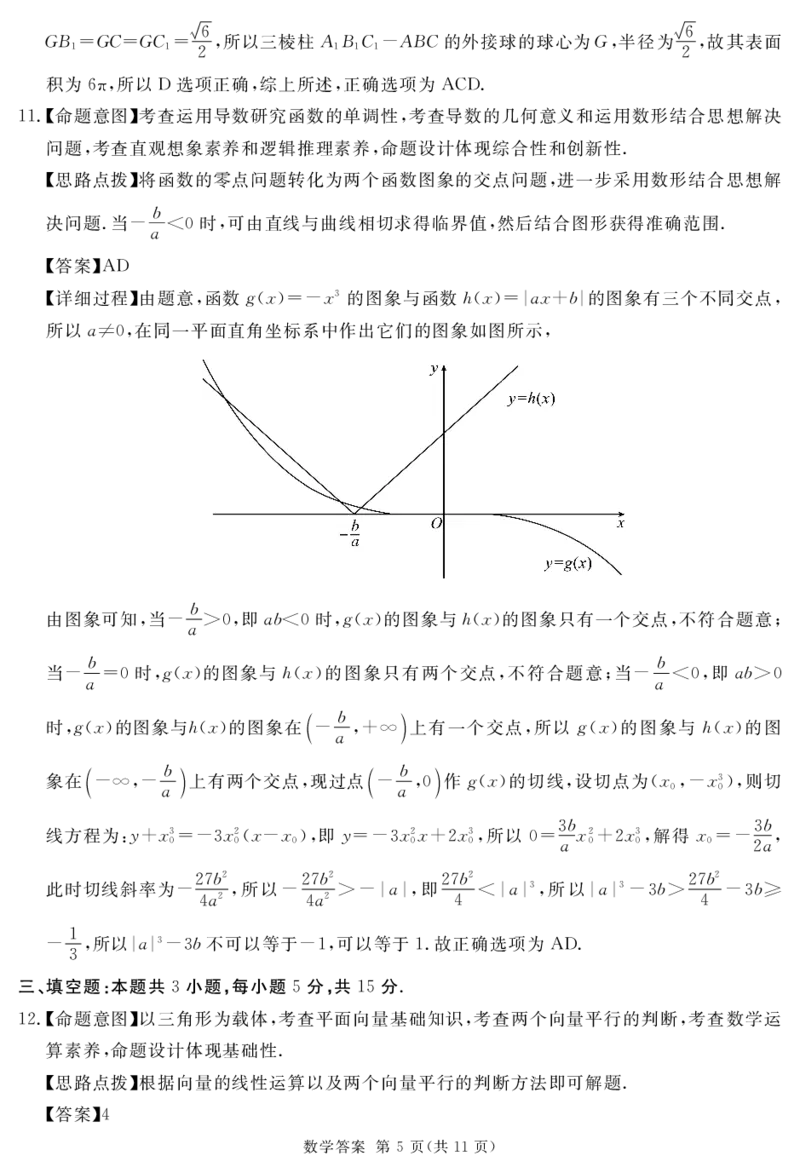
!!!#命题意图$考查运用导数研究函数的单调性%考查导数的几何意义和运用数形结合思想解决
问题%考查直观想象素养和逻辑推理素养%命题设计体现综合性和创新性!
#思路点拨$将函数的零点问题转化为两个函数图象的交点问题%进一步采用数形结合思想解
*
决问题!当, (%时%可由直线与曲线相切求得临界值%然后结合图形获得准确范围!
)
#答案$30
#详细过程$由题意%函数4!%"*,%/ 的图象与函数A!%"*")%)*"的图象有三个不同交点%
所以)’%%在同一平面直角坐标系中作出它们的图象如图所示%
*
由图象可知%当, &%%即)*(%时%4!%"的图象与A!%"的图象只有一个交点%不符合题意)
)
* *
当, *%时%4!%"的图象与A!%"的图象只有两个交点%不符合题意)当, (%%即)*&%
) )
! * "
时%4!%"的图象与A!%"的图象在 , %). 上有一个交点%所以4!%"的图象与A!%"的图
)
! *" ! * "
象在 ,.%, 上有两个交点%现过点 , %% 作4!%"的切线%设切点为!%%,%/"%则切
) ) % %
/* /*
线方程为*&)%/*,/%(!%,%"%即&*,/%(%)(%/%所以%* %()(%/%解得%*, %
% % % % % ) % % % ()
(8*( (8*( (8*( (8*(
此时切线斜率为, %所以, &,")"%即 (")"/%所以")"/,/*& ,/*+
$)( $)( $ $
!
, %所以")"/,/*不可以等于,!%可以等于!!故正确选项为30&
/
三!填空题"本题共/小题#每小题#分#共!#分!
!(!#命题意图$以三角形为载体%考查平面向量基础知识%考查两个向量平行的判断%考查数学运
算素养%命题设计体现基础性!
#思路点拨$根据向量的线性运算以及两个向量平行的判断方法即可解题!
#答案$$
数学答案 第!!!!#页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}33* 33* 33* 33* 33* 33* 33* 33* ’)(33* 33*
#详细过程$由题意%-#*-$)$#%(.#)’.$*(!.$)$#")’.$* -$)($#%
/
33* 33* 33* ’)(
因为(.#)’.$与#-平行%所以 *(%解得’*$!故填$!
/
!/!#命题意图$考查抛物线的定义%考查三角形面积的求解%考查直观想象和数学运算素养%命题
设计体现基础性!
#思路点拨$由抛物线的定义可求得#%$两点的坐标%进而运用分割法表达三角形的面积%代
入相关数据求得答案!当然%三角形面积也可以用弦长"#$"和点B到直线#$的距离求解
/槡(
#答案$
(
#详细过程$不妨设#在第一象限%$在第四象限%则有"#="*% )!*/%"$="*% )!*
# $
/ !
%解得% *(%%* %又因为#%$两点在-上%所以& *(槡(%&*,槡(%易证直线#$经
( # $ ( # $
! /槡( /槡(
过=%所以1B#$的面积C* "B=""& ,&"* %故填 !
( # $ ( (
!$!#命题意图$考查数列与二项式定理综合问题%考查逻辑推理和数学运算等素养%命题设计体
现综合性和创新性!
#思路点拨$由条件运用累加法结合二项式定理求得) *!,!"33%进一步可得到(!))
3)! !
3
)).)) "*(3)!,!"33)3%从而求得)))).)) *(3,!) ’!)!,!"3(!
( 3)! ! ( 3)! (
3
#答案$第一空为!,!"33%第二空为(3,!) ’!)!,!"3(
(
#详细过程$由题意%!,!"(),!,!"!)*,!,!"!-!%!,!"/),!,!"()*,!,!"(-(%
( ! 3 / ( 3
!,!"$),!,!"/)*,!,!"/-/%.%!,!"3)!) ,!,!"3)*,!,!"3-3%将这3个等式
$ / 3 3)! 3 3
两边分别相加得%
!,!"3)!) ,!,!"!)*,’!,!"!-!)!,!"(-()!,!"/-/).)!,!"3-3(
3)! ! 3 3 3 3
*,’!!,!"3,!(*!%所以!,!"3)!) *!,!"!))!*,3%所以) *!,!"33%所以
3)! ! 3)!
(!)))).)) "*-!)-()-/).)-3)))) *(3)!,!"33)3%
! ( 3)! 3 3 3 3 ! 3)!
3
所以)))).)) *(3,!) ’!)!,!"3(!
! ( 3)! (
3
故第一空填!,!"33%第二空填(3,!) ’!)!,!"3(!
(
四!解答题"本题共#小题#共88分!解答应写出文字说明!证明过程或演算步骤!
!#!#命题意图$考查立体几何中垂直关系的证明%考查运用空间向量解决几何问题的能力%考查
逻辑推理和数学运算素养%命题设计体现基础性和应用性!
#思路点拨$第!!"问运用直线与平面垂直的判定定理证得-.0平面C#$%从而证明#$0
-.!第!("问以B为坐标原点%建立空间直角坐标系%接着求得两个平面的法向量%然后运用
向量的夹角公式求得结果!
数学答案 第!!!!5页!共!!页"
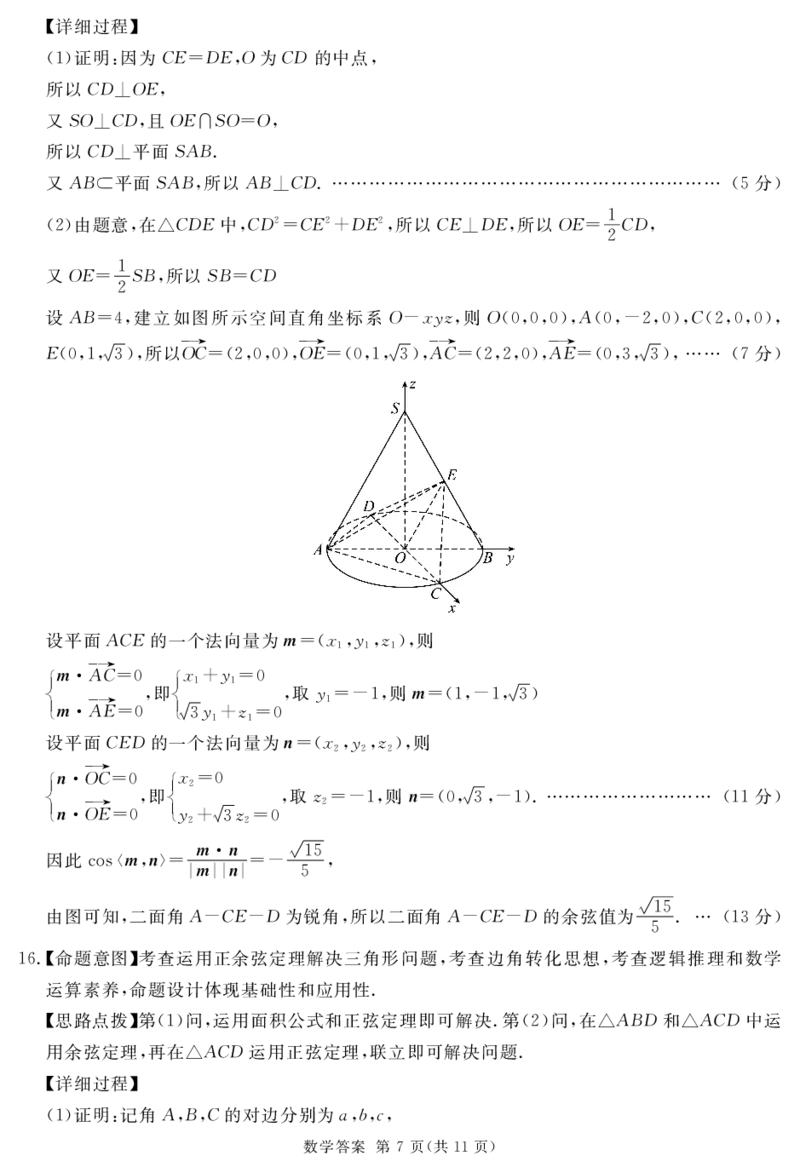
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}#详细过程$
!!"证明*因为-/*./%B为-.的中点%
所以-.0B/%
又CB0-.%且B/2CB*B%
所以-.0平面C#$!
又#$4平面C#$%所以#$0-.!……………………………………………………… !#分"
!
!("由题意%在1-./中%-.(*-/()./(%所以-/0./%所以B/* -.%
(
!
又B/* C$%所以C$*-.
(
设#$*$%建立如图所示空间直角坐标系B,%&"%则B!%%%%%"%#!%%,(%%"%-!(%%%%"%
33* 33* 33* 33*
/!%%!%槡/"%所以B-*!(%%%%"%B/*!%%!%槡/"%#-*!(%(%%"%#/*!%%/%槡/"%…… !8分"
设平面#-/的一个法向量为!*!%%&%""%则
! ! !
33*
6!-#-*% 6%
!
)&
!
*%
5 33* %即5 %取& ! *,!%则!*!!%,!%槡/"
7!-#/*% 7槡/&)"*%
! !
设平面-/.的一个法向量为"*!%%&%""%则
( ( (
33*
6"-B-*% 6%
(
*%
5 33* %即5 %取" ( *,!%则"*!%%槡/%,!"!……………………… !!!分"
7"-B/*% 7&)槡/"*%
( (
!-" 槡!#
因此;<6/!%"0* *, %
"!"""" #
槡!#
由图可知%二面角#,-/,.为锐角%所以二面角#,-/,.的余弦值为 !… !!/分"
#
!5!#命题意图$考查运用正余弦定理解决三角形问题%考查边角转化思想%考查逻辑推理和数学
运算素养%命题设计体现基础性和应用性!
#思路点拨$第!!"问%运用面积公式和正弦定理即可解决!第!("问%在1#$.和1#-.中运
用余弦定理%再在1#-.运用正弦定理%联立即可解决问题!
#详细过程$
!!"证明*记角#%$%-的对边分别为)%*%+%
数学答案 第!!!!8页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}! !
由题意%)*6+7-* +(%
( #
! !
由正弦定理得% 6+7#6+7$6+7-* 6+7(-……………………………………………… !/分"
( #
因为6+7-’%%
#
所以6+7-* 6+7#6+7$!………………………………………………………………… !#分"
(
)( 槡(
!("在1#$.中%由余弦定理得%+(*#.() ) )#.#
$ (
)( 槡(
同理%在1#-.中%*(*#.() , )#.$
$ (
#,$得%+(,*(*槡()#.!……………………………………………………………… !!!分"
6+7-
在1#-.中%由正弦定理得%#.* #-*槡(*6+7-%
6+7/#.-
$ +
所以+(,*(*()*6+7-* +(%即 *槡#%
# *
#$ +
所以 * *槡#! ……………………………………………………………………… !!#分"
#- *
!8!#命题意图$考查运用导数研究函数单调性和最值的能力%考查分类讨论思想%考查数学运算
等素养%命题设计体现基础性和应用性!
!
#思路点拨$第!!"问%构造函数4!%"*?7!%)!") %研究函数4!%"的单调性和最值%从
%)!
而证得结论!第!("问%将不等式恒成立问题转化为研究函数的最值问题%运用分类讨论思想
解决问题!
#详细过程$
!!"证明*1!%"的定义域为!,!%)."!
!
当)+%时%)%(+%%要证1!%"+!%只需证?7!%)!") +!……………………… !(分"
%)!
! %
令4!%"*?7!%)!") %则42!%"* %令42!%"*%%得%*%%
%)! !%)!"(
所以当,!(%(%时%42!%"(%%4!%"在!,!%%"上单调递减)
当%&%时%42!%"&%%4!%"在!%%)."上单调递增!
!
所以4!%"+4!%"*!%即?7!%)!") +!!证毕 …………………………………… !#分"
%)!
(
!("1!%")1!,%"*?7!!,%(") )()%(%
!,%(
(
令D*!,%(%由题意%?7D) ,()D)(),(+%在D)!%%!(时恒成立 ………………… !8分"
D
(
设A!D"*?7D) ,()D)(),(%D)!%%!(!
D
数学答案 第!!!!"页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}! ( ,()D()D,(
则A2!D"* D , D( ,()* D( %令 " !D"*,()D()D,(%
!
当)+, 时%
"
!D"#D()D,(#%%所以A2!D"#%%A!D"在!%%!(上单调递减%所以A!D"+A!!"
(
*%%符合题意 …………………………………………………………………………… !!!分"
!
当)(, ( 时% " !D"在!%%!"上单调递增%又 " !%"*,((%% " !!"*,(),!&%%所以存在D % )
!%%!"%使得
"
!D
%
"*%%且D
%
(D(!时%
"
!D"&%%即A2!D"&%%所以A!D"在!D
%
%!(上单调递增%所
以A!D"#A!!"*%%不符合题意 ………………………………………………………… !!$分"
!
综上所述%)的取值范围为’, %)."………………………………………………… !!#分"
(
!"!#命题意图$考查双曲线的标准方程%考查直线与双曲线的位置关系问题%考查运用代数方法
研究几何问题的能力%考查数学运算和逻辑推理素养%命题设计体现综合性和创新性!
#思路点拨$第!!"问%根据题干条件%不难求得双曲线的标准方程!第!("问%求得直线#/与
!
直线$.的方程之后%求得其交点的纵坐标为&*, %从而证得结论!第!/"问%首先证得点
(
/在以线段$.为直径的圆上%接着再证明过$%.%/三点的圆经过定点#!%%!"!
#详细过程$
%(
!!"由题意%)*!%+*(%所以**槡+(,)(*槡/%所以-的方程为&(, *!! ……… !/分"
/
!("!%"由题意%直线$.的斜率存在%设直线$.方程为*&*3%,(%$!%%&"%.!%%&"!
! ! ( (
6 %(
&(, *!
由5 / %消去&整理得%!/3(,!"%(,!(3%)2*%
7&*3%,(
6 !(3
%)%*
! ( /3(,!
!
所以/3(,!&%%即3(& %5 …………………………………………… !5分"
/
2
%%*
7! ( /3(,!
6 &(,
%(
*!
! 53 / /3()!
所以D*
(
!%
!
)%
(
"*
/3(,!
%由5
53
解得&*@
/3(,!
%
%*
7 /3(,!
! 53 /3()!"
所以/ %, ……………………………………………………………… !"分"
/3(,! /3(,!
/3()!
!)
/3(,!
所以直线#/方程为*&* %)!%即&*,3%)!%
53
,
/3(,!
6&*3%,(
! !
由5 得&*, %所以直线#/与直线$.的交点在一条定直线&*, 上! …
( (
7&*,3%)!
………………………………………………………………………………………… !!%分"
数学答案 第!!!!2页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}!&"过$%.%/三点的圆经过定点%理由如下*
!!(3 "( /5
由弦长公式"$."*槡!)3(槡!%)%"(,$%% *槡!)3(槡 ,
! ( ! ( /3(,! /3(,!
53()5
* !………………………………………………………………………………… !!(分"
/3(,!
(
设线段$.的中点为?!D%&"%则&*3D,(* %
% % /3(,!
( /3()! /3()/
所以"/?"* ) * %
/3(,! /3(,! /3(,!
所以"$."*("/?"%即点/在以线段$.为直径的圆上!…………………………… !!$分"
! 53 "( ! ( "( /3()/
又"#?"*槡 ) ,! * %即"#?"*"/?"%
/3(,! /3(,! /3(,!
所以#在以线段$.为直径的圆上%
所以过$%.%/三点的圆经过定点#!%%!"!…………………………………………… !!8分"
!2!#命题意图$考查数列新定义问题%考查分析问题和解决问题的能力%考查逻辑推理和数学运
算素养%命题设计体现综合性和创新性!
#思路点拨$第!!"问%根据题干条件%不难判断1)2为0!(%,("数列)第!("问%根据条件得到
(
) )) ).)) *!),(")!),$").)!),(3"%再结合等差数列化简证明)第!/"
(,! (,( (,3 ( ( (
问%根据1)2既是0!/%%"数列%又是0!5%%"数列%列出两个方程%分析两个方程中项的下标%
(
从而推出数列1)2为等差数列%进一步根据条件求得%的值!
(
#详细过程$
! !"(
!!"因为)* , %
( (
! !"(,! ! !"(,( ! !"(
所以) )) * , ) , *( , *()*(!),()("
(,! (,( ( ( ( ( (
所以数列1)2是0!(%,("数列!………………………………………………………… !(分"
(
!("证明*因为1)2是公差为(的等差数列
(
所以) )) ).)) *!),(")!),$").)!),(3"
(,! (,( (,3 ( ( (
3!()(3"
*3),!()$).)(3"*3), *3),3(,3*3!),3,!"
( ( ( ( (
所以%对任意3)# %公差为(的等差数列1)2都是0!3%!"数列!…………………… !#分"
) (
!/"证明*由题意%) )) )) */),/%,2!(+$"#
(,! (,( (,/ (
) )) )) )) )) )) *5),5%,/5!(+8"$
(,! (,( (,/ (,$ (,# (,5 (
$,#得%) )) )) */),/%,(8!(+8"
(,$ (,# (,5 (
所以) )) )) */) ,/%,(8!(+$"’
(,! (,( (,/ ()/
由#%’得%/) ,/%,(8*/),/%,2
()/ (
所以) ,)*5!(+$"!………………………………………………………………… !"分"
()/ (
由#得%))) )) */) ,/%,2!(+/"(
( (,! (,( ()!
数学答案 第!!!!%页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}(,#得%),) */) ,/)!(+$"
( (,/ ()! (
即/) *$),) !(+$"
()! ( (,/
所以/) *$) ,)*/) )) ,)*/) )5!(+$"
()$ ()/ ( ()/ ()/ ( ()/
所以) ,) *(!(+$"
()$ ()/
所以) ,)*(!(+8"………………………………………………………………… !!!分"
()! (
在’中%分别令(*$%#%5%8%得
)))))*/),/%,(8)
! ( / 8
)))))*/),/%,(8*
( / $ "
)))))*/),/%,(8+
/ $ # 2
)))))*/) ,/%,(8,
$ # 5 !%
则*,)得%),)*/!),)"*5
$ ! " 8
+,*得%),)*/!),)"*5
# ( 2 "
,,+得%),)*/!) ,)"*5
5 / !% 2
所以) ,)*5!(+!"
()/ (
所以) ,)*(!(+$"………………………………………………………………… !!$分"
()! (
另一方面%由,,+得%),)*/!) ,)",!),)",!),)"*(
$ / !% 2 # $ 5 #
+,*得%),)*/!),)",!),)",!),)"*(
/ ( 2 " $ / # $
*,)得%),)*/!),)",!),)",!),)"*(
( ! " 8 / ( $ /
所以) ,)*(!(+!"
()! (
所以数列1)2是公差为(的等差数列!
(
由)得%/%*/),!)))))",(8*/),/),(8*/
8 ! ( / 8 (
所以%*!!………………………………………………………………………………… !!8分"
数学答案 第!!!!!页!共!!页"
{#{QQABRQSAggAAAhAAARhCEwEiCgMQkhCACagOQBAIIAABSBNABAA=}#}