文档内容
2024—2025学年第二学期高二年级第一次学业诊断检测 A. B. C. D.
数学试题 6.已知事件A,B互斥,它们都不发生的概率为 ,且 ,则 ( )
考试时间:120分钟 考试分值:150分
A. B. C. D.
一、单选题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只
有一项是符合题目要求的。) 7.等比数列 的各项均为正数,且 ,则 (
1.现有3幅不同的油画,4幅不同的国画,5幅不同的水彩画,从这些画中选一幅布置房间,则
).
不同的选法共有( )
A. B.5 C. D.30
A.10种 B.12种 C.20种 D.36种
2.某同学为了让自己渐渐养成爱运动的习惯,制定一个十天的运动习惯养成计划,他决定第一
8.已知双曲线C: 的左、右焦点分别为 , ,直线 经过 ,且与C
天运动10分钟,从第二天起,每天运动的时长比前一天多5分钟.根据这个计划,该同学第十
天的运动时长为( )
交于A,B两点,若 , ,则 的离心率为( )
A.45分钟 B.50分钟 C.55分钟 D.60分钟
A. B. C. D.
3.若 ,则 ( )
A.121 B.122 C. D. 二、多选题(本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.)
4.抛掷一枚质地均匀且各个面上分别标有数字 的正方体玩具.设事件 为“向上一
9.设数列 的前 项和为 ,已知 ,则下列结论正确的是( )
面点数为偶数”,事件 为“向上一面点数为6的约数”,则 等于( )
A. B.数列 为等比数列
A. B. C. D.
5.记 为等差数列 的前 项和,已知 , ,则 ( ) C. D.若 ,则数列 的前10项和为10.已知直线 ,圆 ,则( )
14.直线 与椭圆 恒有公共点,则实数 的取值范围是 .
A. 经过定点 B.圆 与圆 : 外离
四、解答题(本题共5小题,共77分解答应写出必要的文字说明,证明过程或演算步
骤)
C.当 与圆 相切时, . D.圆心 到直线 距离的最大值为
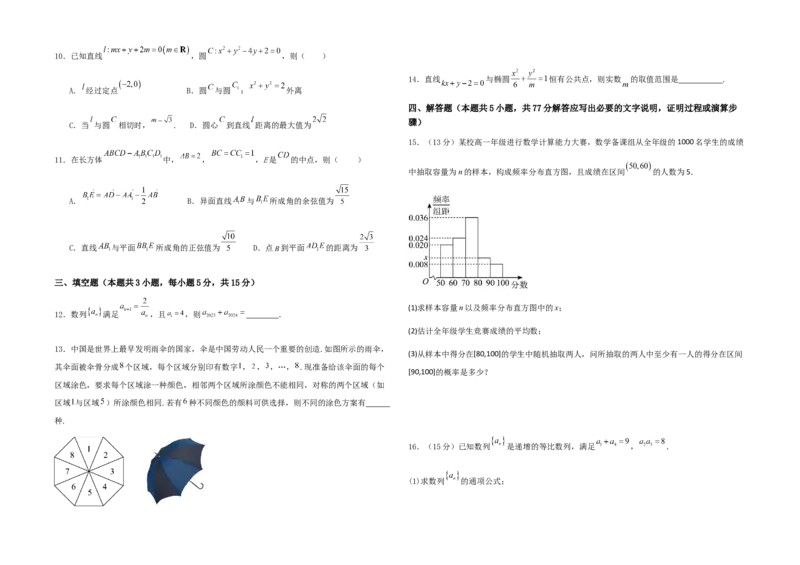
15.(13分)某校高一年级进行数学计算能力大赛,数学备课组从全年级的1000名学生的成绩
11.在长方体 中, , ,E是 的中点,则( )
中抽取容量为n的样本,构成频率分布直方图,且成绩在区间 的人数为5.
A. B.异面直线 与 所成角的余弦值为
C.直线 与平面 所成角的正弦值为 D.点 到平面 的距离为
三、填空题(本题共3小题,每小题5分,共15分)
(1)求样本容量n以及频率分布直方图中的x;
12.数列 满足 ,且 ,则 .
(2)估计全年级学生竞赛成绩的平均数;
13.中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示的雨伞,
(3)从样本中得分在[80,100]的学生中随机抽取两人,问所抽取的两人中至少有一人的得分在区间
其伞面被伞骨分成 个区域,每个区域分别印有数字 , , ,…, .现准备给该伞面的每个
[90,100]的概率是多少?
区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能相同,对称的两个区域(如
区域 与区域 )所涂颜色相同.若有 种不同颜色的颜料可供选择,则不同的涂色方案有
种.
16.(15分)已知数列 是递增的等比数列,满足 , .
(1)求数列 的通项公式;(2)若 ,求数列 的前 项和 .
17.(15分)如图,三棱柱 中,四边形 是边长为2的正方形, , 分别 19.(17分)已知抛物线C: ( )经过点 ( ),F为焦点,且
为 , 的中点, 与 交于点 ,若 ,且平面 平面 . .
(1)求C的方程及 ;
(2)设O为原点,过F作斜率不为0的直线l交C于M,N两点,直线 分别交直线OM,ON于
A,B.证明:以AB为直径的圆经过x轴上的两个定点.
(1)求证: 平面 ;
(2)若三棱柱 的体积为4,求锐二面角 的余弦值.
18.(17分)已知数列 满足 .
(1)设 ,写出 ;
(2)证明数列 为等比数列;
(3)求数列 的前 项和 .