余姚中学2024学年第二学期质量检测高二数学学科试卷参考答案_2024-2025高二（7-7月题库）_2025年03月试卷_0320浙江省余姚中学2024-2025学年高二下学期3月月考试题_高二数学

余姚中学 2024 学年第二学期质量检测高二数学学科试卷参考答案 一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目 要求的. 题号 1 2 3 4 5 6 7 8 答案 Ｂ Ｃ Ａ Ｄ Ｃ Ａ Ａ Ｂ f (x) 8.【解析】令g(x)= ，所以 f (x)=e2xg(x)，因为 f (x)+e4xf (−x)=0，所以 e2x e2xg(x)+e4xe−2xg(−x)=0，化简得g(x)+g(−x)=0， 所以g(x)是(−3,3)上的奇函数； f(x)e2x−2e2xf (x) f(x)−2f (x) g(x)= = ， e4x e2x 因为当0x3时， f(x)2f (x)， 所以当x0,3)时，g(x)0，从而g(x)在0,3)上单调递增，又g(x)是(−3,3)上的奇函数，所以g(x)在 (−3,3)上单调递增； f (1) e2 考虑到g(1)= = =1，由e2xf (2−x)e4， e2 e2 得e2xe2(2−x)g(2−x)e4，即g(2−x)1= g(1)， −32−x3, 由g(x)在(−3,3)上单调递增，得 解得1x5，  2−x1, 所以不等式e2xf (2−x)e4的解集为(1,5)， 故选：B. 二、多项选择题：本题共3小题，每小题6分，共18分，在每小题给出的四个选项中，有多项符合题目 的要求，全部选对的得6分，部分选对的得部分分，有选错的得0分。 题号 9 10 11 答案 BCD ABD BCD 11.【解答】∵(1−𝑥)2025 =𝑎 +𝑎 𝑥+𝑎 𝑥2+⋯+𝑎 𝑥2025， 0 1 2 2025 展开式的各二项式系数的和为22025，所以A错； 令𝑥 =0，得到𝑎 =1，令𝑥 =1，得到𝑎 +𝑎 +𝑎 +⋯+𝑎 =0， 0 0 1 2 2025 ∴𝑎 +𝑎 +⋯+𝑎 =−1，所以B对； 1 2 2025 由二项式定理可得：C𝑘 (−𝑥)𝑘 =C𝑘 (−1)𝑘𝑥𝑘，𝑎 =C𝑘 (−1)𝑘， 2025 2025 𝑘 2025 所以22025−𝑘𝑎 =22025−𝑘C𝑘 (−1)𝑘，𝑘 =0,1,2⋯,2025， 𝑘 202522025C0 (−1)0+22024C1 (−1)1+22023C2 (−1)2+⋯+20C2025(−1)2025 =(2+(−1)) 2025 =1， 2025 2025 2025 2025 ∴22025𝑎 +22024𝑎 +22023𝑎 +⋯+𝑎 =1，故C对； 0 1 2 2025 𝑎 =C𝑘 (−1)𝑘,𝑘 =0,1⋯,2025， 𝑘 2025 1 𝑘!(𝑛−𝑘)! 𝑛+1 𝑘!(𝑛−𝑘)!(𝑛+2) 𝑛+1 𝑘!(𝑛−𝑘)!(𝑘+1+𝑛+1−𝑘) = = ⋅ = ⋅ C𝑘 𝑛! 𝑛+2 (𝑛+1)! 𝑛+2 (𝑛+1)! 𝑛 𝑛+1 𝑘!(𝑛+1−𝑘)! (𝑘+1)!(𝑛−𝑘)! 𝑛+1 1 1 = [ + ]= ( + ) 𝑛+2 (𝑛+1)! (𝑛+1)! 𝑛+2 C𝑘 C𝑘+1 𝑛+1 𝑛+1 ∑ 2025 1 =∑ 2025 1 =∑ 2025 (−1)𝑘 = 1 − 1 + 1 −⋯+(−1)2025 1 ， 𝑘=0 𝑎𝑘 𝑘=0 (−1)𝑘C 2 𝑘 025 𝑘=0 C 2 𝑘 025 C 2 0 025 C 2 1 025 C 2 2 025 C 2 2 0 0 2 2 5 5 1 2026 1 1 = ( + )， C𝑘 2027 C𝑘 C𝑘+1 2025 2026 2026 2025 1 2026 1 1 1 1 1 1 ∑ = [( + )−( + )+⋯+(−1)2025( + )] 𝑎 2027 C0 C1 C1 C2 C2025 C2026 𝑘 2026 2026 2026 2026 2026 2026 𝑘=0 2026 1 1 = ( − )=0 2027 C0 C2026 2026 2026 1 1 1 1 ∵ =1，∴ + +⋯+ =−1，故D对. 𝑎0 𝑎1 𝑎2 𝑎2025 故选：BCD. 三、填空题：本题共3小题，每小题5分，共15分。 12.42 13.420 14.e 14.【解答】依题意得，xex1 −x −e2 =0，即xex1 −x =e2，x 0， 1 1 1 1 1 (x −e)(ln x −1)−e3 =0，即(x −e)(ln x −1)=e3，x e， 2 2 2 2 2 e(xex1 −x )=e3 =(x −e)(lnx −1)， 1 1 2 2 x(ex1+1−e)=(lnx −1)(x −e)， 1 2 2 ， 又 lnx 1，lnx −10， 2 2 同构函数：F(x)=x(ex+1−e)，x0， 则F(x)=F(ln x −1)=e3， 1 2 又F(x)=ex+1−e+xex+1 =e(ex −1)+xex+1， x 0，ex e0 =1，ex −10，又xex+1 0，F(x)0，F(x)单调递增，x =ln x −1， 1 2 x (x −e) (ln x −1)(x −e) e3  1 2 = 2 2 = =e. e2 e2 e2 故答案为e. 四、解答题：本题共5小题，共77分，解答应写出必要的文字说明、证明过程及验算步骤。 1 9 15.在(√𝑥− ) 的展开式中.求 2𝑥 (1)常数项； (2)含𝑥3的项的系数； (3)系数的绝对值最大的项． 【解答】(√𝑥− 1 ) 9 的展开式的通项公式𝑇 𝑟+1 =C 9 𝑟(√𝑥) 9−𝑟 (− 1 ) 𝑟 =(− 1 ) 𝑟 ⋅C 9 𝑟⋅𝑥 9− 2 3𝑟 ,𝑟 =0,1,2,⋅⋅⋅,9， 2𝑥 2𝑥 2 １）令 9−3𝑟 =0，解得𝑟 =3，可得𝑇 =(− 1 ) 3 ⋅C3 =− 21 ， 4 9 2 2 2 21 即常数项为− 2 ２）令 9−3𝑟 =3，解得𝑟 =1，可得𝑇 =− 1 ×C1⋅𝑥3 =− 9 𝑥3， 2 9 2 2 2 即𝑥3项的系数为− 9 ， 2 1 ３）系数的绝对值是Cr( )r，令 9 2  1 1 Ck( )k Ck+1( )k+1   9 2 9 2 7 10   k  1 1 3 3 Ck( )k Ck−1( )k−1  9 2 9 2 kZ k =3 21 系数的绝对值最大的项为T =T =− 3+1 4 2 16. 已知甲袋中有3个白球和4个黑球，乙袋中有5个白球和4个黑球，现在从两个袋 中各取2个球，试求： 1)取得的4个球均是白球的概率； 2)取得白球个数的分布列及数学期望． 5 1)P = 126 6 32 53 30 5 2)P(=0)= ,P(=1)= ,P(=2)= ,P(=3)= ,P(=4)= 126 126 126 126 126 124 E()= 6317. 为深入学习党的二十大精神，某学校团委组织了“青春向党百年 路，奋进学习二十大”知识竞赛活动，并从中抽取了200份试卷进行 调查，这200份试卷的成绩（卷面共100分）频率分布直方图如图. (1)用样本估计总体，求此次知识竞赛的平均分（同一组中的数据用该 组区间的中点值为代表）. (2)可以认为这次竞赛成绩X 近似地服从正态分布N ( ,2) （用样本平均数x 和标准差s分别作为，的 近似值），已知样本标准差s8.65，如有84%的学生的竞赛成绩高于学校期望的平均分，则学校期望的平 均分约为多少（结果取整数）？ (3)从80,100的试卷中用分层抽样的方法抽取10份试卷，再从这10份样本中随机抽测i(1i6)份试卷 （抽测的份数是随机的），若已知抽测的i份试卷都不低于90分，求抽测2份的概率. 参考数据：若X N ( ,2) ，则 P(−X +)0.6827,P(−2X +2)0.9545,P(−3 X +3)0.9973. 【解答】（1）由频率分布直方图可知， 平均分=(650.01+750.04+850.035+950.015)10=80.5； （2）由（1）可知，X N ( 80.5,8.652) , 设学校期望的平均分约为m，则P(X m)=0.84， 因为P(−X +)0.6827，P(−X )0.34135， 所以P(X −)0.84135，即P(X 71.85)0.84， 所以学校的平均分约为72分； （3）由频率分布直方图可知，分数在80,90)和90,100的频率分别为0.35和0.15， 0.35 那么按照分层抽样，抽取10人，其中分数在80,90)，应抽取10 =7人， 0.35+0.15 0.15 分数在90,100应抽取10 =3人， 0.35+0.15 记事件A：抽测i份试卷i=1,2,3，事件B:取出的试卷都不低于90分， i 1 Ci 则P(A)= ,P(B A)= 3 ， i 6 i Ci 10 i=1 1  C1 C2 C3  1 P(B)=P(A)P(B A)=  3 + 3 + 3 = ， 3 i i 6 C1 C2 C3  16 10 10 101 C2  3 P(A B) 6 C2 8 则P(A B)= 2 = 10 = . 2 P(B) 1 45 16 1 18. 已知离心率为2的椭圆E: x2 + y2 =1(ab0)与x轴正半轴､ y 轴正半轴分别交于A､B两点且 a2 b2 AB = 7 . （1）求椭圆E的标准方程； 6 2 （2）设经过椭圆E左焦点F 的直线l与椭圆E交于C,D两点，点O为坐标原点.若 OCD面积为 ， 7 求直线l的方程；  3 3 （3）点Q  1, ，点M､N 在椭圆E上，且满足k +k =− （记直线MQ的斜率为k ，直线NQ  2 MQ NQ 4 MQ 斜率为k ），过点Q作MN的垂线，垂足为H ，问：是否存在定点G，使得 GH 为定值？若存在，求 NQ 出此定值，若不存在，请说明理由. c 1 b 3 【解答】(１)由题意可得e= =  = ，又 a2 +b2 = 7， a 2 a 2 x2 y2 a=2,b= 3，故椭圆E的标准方程为 + =1. 4 3 (２)显然直线l的斜率不会为0，设直线CD:x=ty−1， x2 y2 设C(x ,y ),D(x ,y ) ，则   4 + 3 =1 ，消去x可得 ( 3t2 +4 ) y2 −6ty−9=0， 1 1 2 2  x=ty−1 6t 9 由=144t2 +1440，则y + y = ,y y =− ， 1 2 3t2 +4 1 2 3t2 +4 1 1  6t  2 36 6 t2 +1 6 2 S = OF  y − y = + = = ，解得t =1，   OMN 2 1 2 2 3t2 +4 3t2 +4 3t2 +4 7 所以，直线l的方程为x+y+1=0或x−y+1=0. (３)若直线MN的斜率存在，设直线MN : y =kx+m,M (x ,y ),N(x ,y ) ， 3 3 4 4 x2 y2   4 + 3 =1 ，消y可得 ( 4k2 +3 ) x2 +8kmx+4m2 −12=0，  y =kx+m−8km 4m2 −12 由=192k2−48m2+1440，则x +x = ,x x = ， 3 4 4k2 +3 3 4 4k2 +3 y − 3 y − 3   kx +m− 3  (x −1)+   kx +m− 3  (x −1) 由 3 2 4 2  4 2 3  3 2 4 3， k +k = + = =− MQ NQ x −1 x −1 (x −1)(x −1) 4 3 4 3 4  3  3  即4  kx +m−  (x −1)+  kx +m−  (x −1)  +3(x −1)(x −1)=0，  4 2 3  3 2 4  3 4 整理得 (3+8k)x x +(4m−4k−9)(x +x )+15−8m=0， 3 4 3 4 (3+8k)( 4m2 −12 ) +(4m−4k−9)(−8km)+(15−8m)( 4k2 +3 ) =0， 整理得 (2k+2m−3)(10k+2m−1)=0，2k +2m−3=0或10k+2m−1=0. 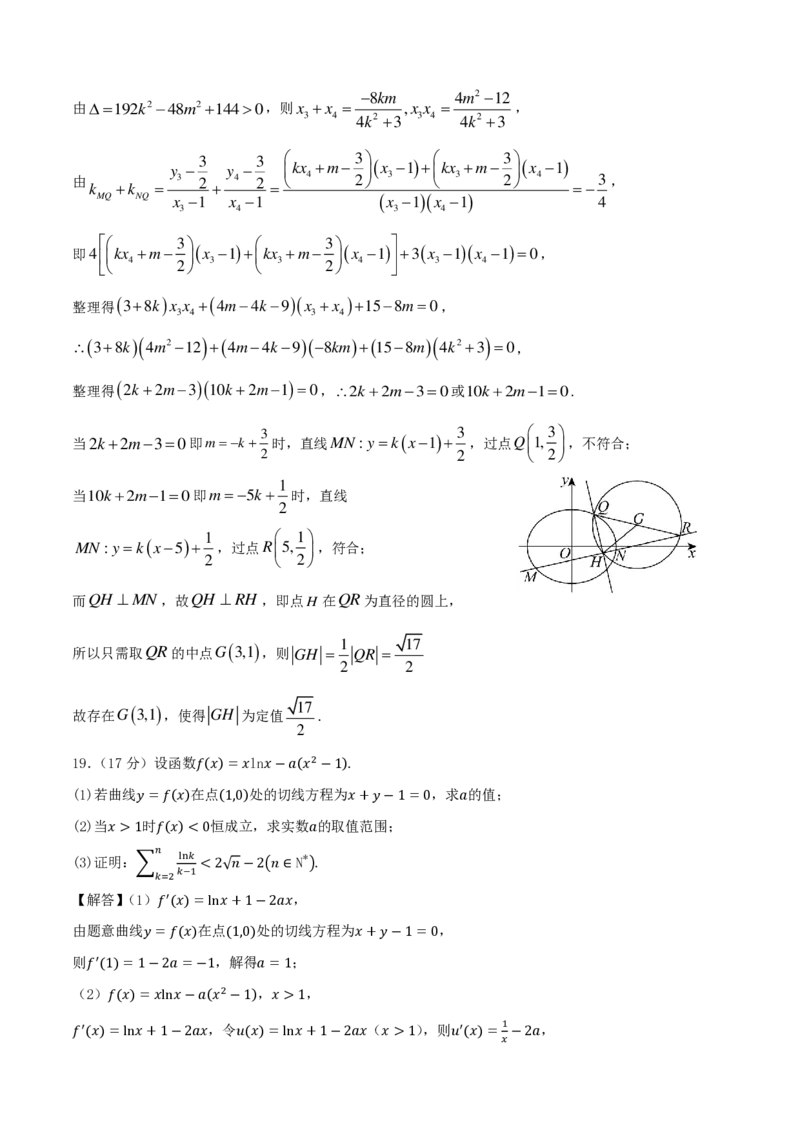3 3  3 当2k+2m−3=0即m=−k+ 时，直线MN:y=k(x−1)+ ，过点Q  1, ，不符合； 2 2  2 1 当10k+2m−1=0即m=−5k+ 时，直线 2 1  1 MN:y =k(x−5)+ ，过点R  5, ，符合； 2  2 而QH ⊥MN，故QH ⊥RH ，即点H 在QR为直径的圆上， 1 17 所以只需取QR的中点G(3,1) ，则 GH = QR = 2 2 17 故存在G(3,1) ，使得 GH 为定值 . 2 19．（17分）设函数𝑓(𝑥)=𝑥ln𝑥−𝑎(𝑥2−1). (1)若曲线𝑦 =𝑓(𝑥)在点(1,0)处的切线方程为𝑥+𝑦−1=0，求𝑎的值； (2)当𝑥 >1时𝑓(𝑥)<0恒成立，求实数𝑎的取值范围； 𝑛 (3)证明：∑ ln𝑘 <2√𝑛−2(𝑛∈N* ). 𝑘−1 𝑘=2 【解答】（1）𝑓′(𝑥)=ln𝑥+1−2𝑎𝑥， 由题意曲线𝑦=𝑓(𝑥)在点(1,0)处的切线方程为𝑥+𝑦−1=0， 则𝑓′(1)=1−2𝑎=−1，解得𝑎 =1； （2）𝑓(𝑥)=𝑥ln𝑥−𝑎(𝑥2−1)，𝑥 >1， 𝑓′(𝑥)=ln𝑥+1−2𝑎𝑥，令𝑢(𝑥)=ln𝑥+1−2𝑎𝑥（𝑥 >1），则𝑢′(𝑥)= 1 −2𝑎， 𝑥当2𝑎≤0，即𝑎 ≤0时，𝑢′(𝑥)>0，𝑢(𝑥)即𝑓′(𝑥)是(1,+∞)上的增函数， 因此𝑓′(𝑥)>𝑓′(1)=1−2𝑎 >0， 𝑓(𝑥)是增函数，所以𝑓(𝑥)>𝑓(1)=0，不合题意，舍去； 当2𝑎≥1即𝑎 ≥ 1 时，𝑢′(𝑥)<0，𝑢(𝑥)即𝑓′(𝑥)是(1,+∞)上的减函数， 2 所以𝑓′(𝑥)<𝑓′(1)=1−2𝑎 ≤0， 所以𝑓(𝑥)是(1,+∞)上的减函数，从而𝑓(𝑥)<𝑓(1)=0恒成立， 1 1 当0<2𝑎 <1即0<𝑎 < 时， >1， 2 2𝑎 𝑥 ∈(1, 1 )时，𝑢′(𝑥)>0，𝑢(𝑥)在(1, 1 )单调递增， 2𝑎 2𝑎 𝑥 ∈( 1 ,+∞)时，𝑢′(𝑥)<0，𝑢(𝑥)在( 1 ,+∞)单调递减， 2𝑎 2𝑎 又𝑢(1)=1−2𝑎>0，所以𝑥 ∈(1, 1 )时，𝑢(𝑥)>0恒成立，即𝑓′(𝑥)>0恒成立， 2𝑎 1 此时𝑓(𝑥)在(1, )上单调递增，因此𝑓(𝑥)>𝑓(1)=0，与题意不合，舍去， 2𝑎 1 综上𝑎 ≥ ． 2 （3）由（2）知𝑥 >1时，𝑥ln𝑥 < 1 (𝑥2−1)，即 2𝑥ln𝑥 <1，从而 2√𝑥ln√𝑥 <1， 2 𝑥2−1 𝑥−1 ln𝑥 1 1 2 2 所以 < ，又 = < =2(√𝑥−√𝑥−1)， 𝑥−1 √𝑥 √𝑥 2√𝑥 √𝑥+√𝑥−1 ln𝑥 所以 <2(√𝑥−√𝑥−1)， 𝑥−1 此不等式中分别令𝑥 =2,3,⋯,𝑛得 ln2 ln3 ln𝑛 <2(√2−1)， <2(√3−√2)，⋯， <2(√𝑛−√𝑛−1)， 1 2 𝑛−1 𝑛 将这𝑛−1个不等式相加得∑ ln𝑘 <2√𝑛−2(𝑛∈N* ). 𝑘−1 𝑘=2