文档内容
2025届高三年级第三次月考数学试卷 .
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一 A B. C. D.
项是符合题目要求的.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符
1. 数据 的 分位数为( )
A. 9 B. 8.5 C. 8 D. 7.5 合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9. 下列说法正确的是( )
2.设平面向量 , 均为单位向量,则“ ”是“ ”的( )
A. 函数 的图像恒过定点
A. 充分而不必要条件 B. 必要而不充分条件
C. 充分必要条件 D. 既不充分也不必要条件 B. “ ”的必要不充分条件是“ ”
3. 甲、乙、丙、丁4个学校将分别组织部分学生开展研学活动,现有 五个研学基
C. 函数 的最小正周期为2
地供选择,每个学校只选择一个基地,则4个学校中至少有3个学校所选研学基地不相同的
选择种数共有( )
D. 函数 的最小值为2
A. 420 B. 460 C. 480 D. 520
4. 已知函数 ,若 ,则实数 的取值范围是( 10. 函数 的部分图象如图所示,点 是图象上的最
高点,点 是图象与 轴的交点,点 在 轴上.若 是等腰直角三角形,则下列结论正
)
确的是( )
A. B. C. D.
5. 已知数列{a}的前n项和为S,且2a-S=2,记数列 的前n项和为
n n n n
T,若对于任意n∈N*,不等式k>T 恒成立,则实数k的取值范围为( )
n n
A. B. C. D.
A. B. 在区间 上单调递增
6. 已知函数 是定义在 上的可导函数,其导函数为 ,若对任意 有
, ,且 ,则不等式 的解集为( C. 的图象关于点 对称 D. 在区间 上有 个极值点
)
A. B. C. D. 11. 已知函数 图象上的点 均满足
7.已知抛物线 过点 ,动点M,N为C上的两点,且直线AM与AN的 对 有
斜率之和为0,直线L的斜率为 ,且过C的焦点F,直线L把 分成面积相等的两部
成立,则( )
分,则直线MN的方程为( )
A. B. A. B. 的极值点为
C. D.
C. D.
8.已知 ,且 ,函数 ,若关于x的方程 有两个不相
三、填空题
等的实数根,则a的取值范围是( ) 12. 的展开式中 的系数为__________.
13. 若直线 与曲线 相切,则 的最小值为__________.
2025届高三年级第三次月考数学试卷--114. 已知圆 ,抛物线 .若对于 上任意一点 ,使得
对圆 上的任意两点A,B,总有 ,则 的取值范围是______.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知平面向量 , ,记 ,
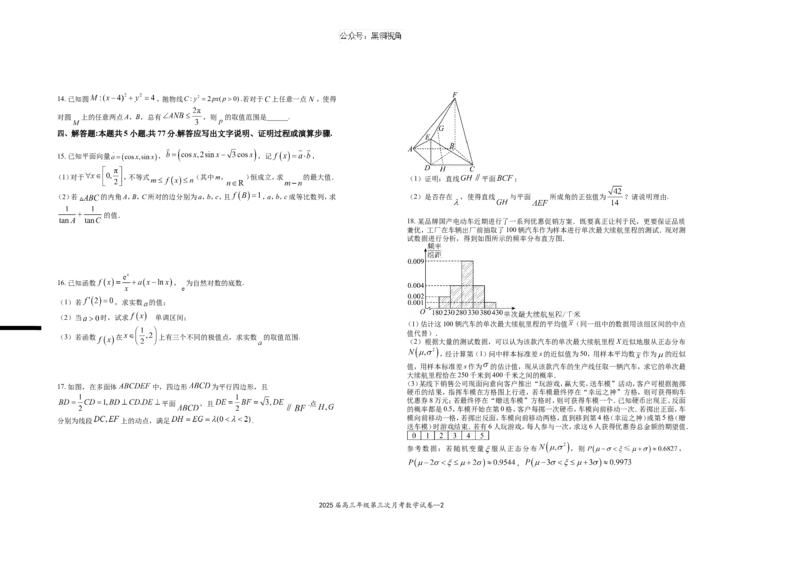
(1)对于 ,不等式 (其中m, )恒成立,求 的最大值. (1)证明:直线 平面 ;
(2)若 的内角A,B,C所对的边分别为a,b,c,且 ,a,b,c成等比数列,求 (2)是否存在 ,使得直线 与平面 所成角的正弦值为 ?请说明理由.
的值.
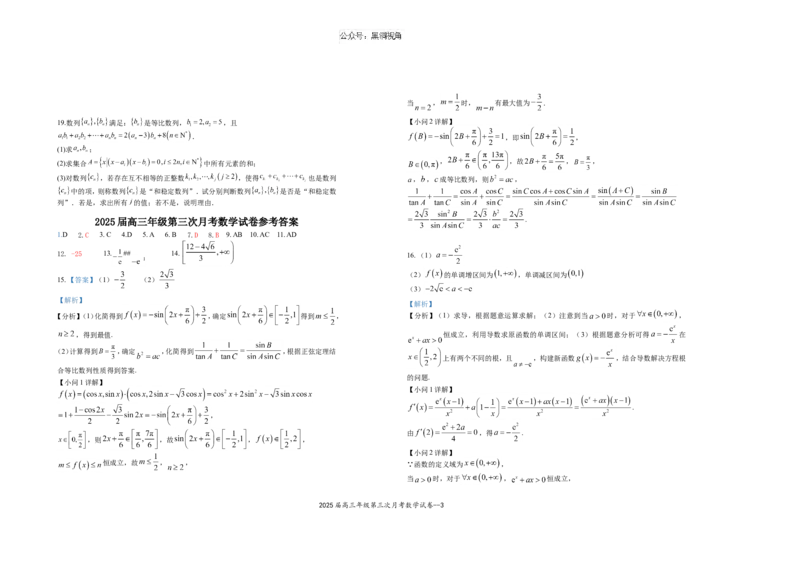
18. 某品牌国产电动车近期进行了一系列优惠促销方案.既要真正让利于民,更要保证品质
兼优,工厂在车辆出厂前抽取了100辆汽车作为样本进行单次最大续航里程的测试.现对测
试数据进行分析,得到如图所示的频率分布直方图.
16. 已知函数 , 为自然对数的底数.
(1)若 ,求实数 的值;
(2)当 时,试求 的单调区间;
(1)估计这100辆汽车的单次最大续航里程的平均值 (同一组中的数据用该组区间的中点
值代替).
(3)若函数 在 上有三个不同的极值点,求实数 的取值范围.
(2)根据大量的测试数据,可以认为该款汽车的单次最大续航里程X近似地服从正态分布
,经计算第(1)问中样本标准差s的近似值为50,用样本平均数 作为 的近似
值,用样本标准差s作为 的估计值,现从该款汽车的生产线任取一辆汽车,求它的单次最
大续航里程恰在250千米到400千米之间的概率.
(3)某线下销售公司现面向意向客户推出“玩游戏,赢大奖,送车模”活动,客户可根据抛掷
17. 如图,在多面体 中,四边形 为平行四边形,且
硬币的结果,指挥车模在方格图上行进,若车模最终停在“幸运之神”方格,则可获得购车
优惠券8万元;若最终停在“赠送车模”方格时,则可获得车模一个.已知硬币出现正、反面
平面 ,且 .点
的概率都是0.5,车模开始在第0格,客户每掷一次硬币,车模向前移动一次.若掷出正面,车
模向前移动一格,若掷出反面,车模向前移动两格,直到移到第4格(幸运之神)或第5格(赠
分别为线段 上的动点,满足 .
送车模)时游戏结束.若有6人玩游戏,每人参与一次,求这6人获得优惠券总金额的期望值.
参考数据:若随机变量 服从正态分布 ,则 ,
,
2025届高三年级第三次月考数学试卷--2当 , 时, 有最大值为 .
19.数列 满足: 是等比数列, ,且 【小问2详解】
. ,即 ,
(1)求 ;
, ,故 , ,
(2)求集合 中所有元素的和;
(3)对数列 ,若存在互不相等的正整数 ,使得 也是数列 , , 成等比数列,则 ,
中的项,则称数列 是“和稳定数列”.试分别判断数列 是否是“和稳定数
列”.若是,求出所有 的值;若不是,说明理由.
2025届高三年级第三次月考数学试卷参考答案 .
1.D 2.C 3. C 4.D 5. A 6. B 7.D 8.B 9. AB 10. AC 11. AD
12. -25 13. ## 14. 16. (1)
(2) 的单调增区间为 ,单调减区间为
15. 【答案】(1) (2)
(3)
【解析】
【解析】
【分析】(1)化简得到 ,确定 得到 , 【分析】(1)求导,根据题意运算求解;(2)注意到当 时,对于 ,
,得到最值. 恒成立,利用导数求原函数的单调区间;(3)根据题意分析可得 在
(2)计算得到 ,确定 ,化简得到 ,根据正弦定理结
上有两个不同的根,且 ,构建新函数 ,结合导数解决方程根
合等比数列性质得到答案.
的问题.
【小问1详解】
【小问1详解】
.
,
由 ,得 .
,则 ,故 , ,
【小问2详解】
恒成立,故 , , ∵函数的定义域为 ,
当 时,对于 , 恒成立,
2025届高三年级第三次月考数学试卷--3∴当 , ,当 , ,
故 的单调增区间为 ,单调减区间为 .
【小问3详解】
由条件可知 ,在 上有三个不同的根,
∵ 是 的根,
∴ ,即 在 上有两个不同的根,且 , .
.
令 ,则 ,
设平面 的法向量为 ,
∵当 时, ,当 时, ,
则由 ,取 得 .
则 在 上单调递增,在 上单调递减,
因为 ,所以
∴ 的最大值为 ,且 , ,
解得 .
又∵ ,即 ,
所以 ,且 平面 ,所以 平面
∴ , 【小问2详解】
设平面 的法向量为
故 .
17. (1)证明见解析 (2)存在,理由见解析 则由 ,解得 .
【解析】
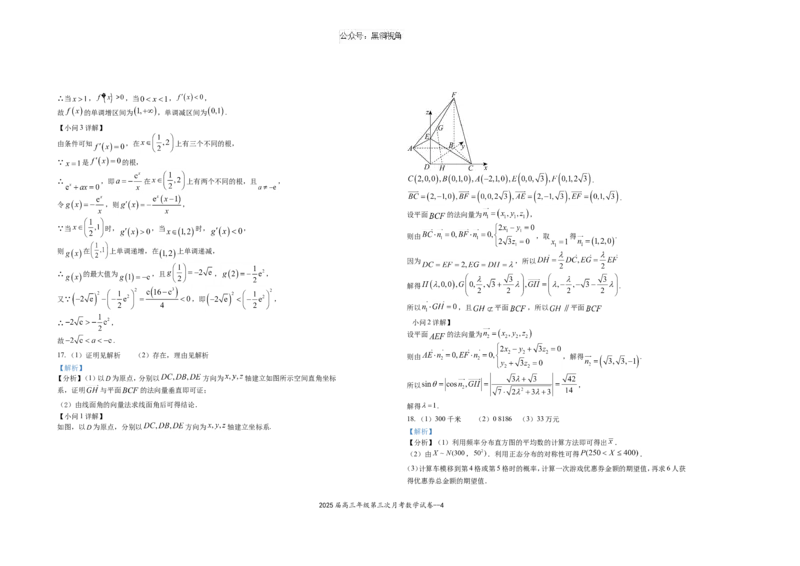
【分析】(1)以 为原点,分别以 方向为 轴建立如图所示空间直角坐标
所以 ,
系,证明 与平面 的法向量垂直即可证;
(2)由线面角的向量法求线面角后可得结论. 解得 .
.
【小问1详解】
18. (1)300千米 (2)08186 (3)33万元
如图,以 为原点,分别以 方向为 轴建立坐标系.
【解析】
【分析】(1)利用频率分布直方图的平均数的计算方法即可得出 .
(2)由 , .利用正态分布的对称性可得 .
(3)计算车模移到第4格或第5格时的概率,计算一次游戏优惠券金额的期望值,再求6人获
得优惠券总金额的期望值.
2025届高三年级第三次月考数学试卷--4【小问1详解】
估计这100辆汽车的单次最大续航里程的平均值为: 【分析】(1)根据已知及等比数列的定义求出 的通项公式,由已知和求通项可得 的通
项公式,
千米 (2)根据等差数列及等比数列的求和公式可得结果
【小问2详解】 (3)根据“和稳定数列”的定义可判定.
由 ,它的单次最大续航里程恰在250千米到400千米之间的概率为: 【详解】(1) ,
又 , ,解得:
.
因为 是等比数列,所以 的公比 ,
【小问3详解】
硬币出现正、反面的概率都是 , 又当 时, ,
作差得:
第一次掷出正面,车模移动到第1格,其概率为 ,
将 代入,化简: ,
得:
移动到第2格有两类情况:掷出2次正面或掷出1次反面, ,
是公差 的等差数列,
同理, , (2)记集合 的全体元素的和为 ,
集合 的所有元素的和为 ,
,
集合 的所有元素的和为 ,
,
集合 的所有元素的和为 ,则有
设参与游戏一次的顾客获得优惠券金额为X万元, 或0,
对于数列 :
∴X的期望 万元
当 时, 是数列 中的项
设这6人获得优惠券总金额为Y万元,优惠券总金额的期望值 当 时, 不是数列 中的项
万元.
,其中
即 (其中 表示不超过实数 的最大整数)
19.(1) ,
(2)
(3)数列 是“和稳定数列”, ,数列 不是“和稳定数列”,理由见
解析 (3)①解:当 时, 是 的正整数倍,
2025届高三年级第三次月考数学试卷--5故一定不是数列 中的项;
当 时, ,不是数列 中的项;
当 时, ,是数列 中的项;
综上,数列 是“和稳定数列”, ;
②解:数列 不是“和稳定数列”,理由如下:
不妨设: ,则 ,且
故 不是数列 中的项.
数列 不是“和稳定数列”.
2025届高三年级第三次月考数学试卷--6