文档内容
东北三省精准教学 2024 年 12 月高三联考
数学
本试卷满分150分,考试用时120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在
本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.已知复数 (i为虚数单位),则|z|=
A.2 B. C. D.1
2.已知 ,则“ ”是“ ”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知向量 , ,且 ,则
A.3 B. C. D.
4.已知函数 ( , , , )的部分图象如图所示,则下列
说法正确的是A.直线 是f(x)图象的一条对称轴
B.f(x)图象的对称中心为 ,
C.f(x)在区间 上单调递增
D.将f(x)的图象向左平移 个单位长度后,可得到一个偶函数的图象
5.正四棱台在古代被称为“方亭”,在中国古代建筑中有着广泛的应用.例如,古代园林中的台榭建筑
常常采用这种结构,台上建有屋宇,称为“榭”,这种结构不仅美观,还具有广瞻四方的功能,常用于观
赏和娱乐.在正四棱台ABCD-A′B′C′D′中, , , ,则
A.2 B. C. D.3
6.已知等比数列 的前n项和为 ,且 ,其中 .若在 与 之间插入3个数,
使这5个数组成一个公差为d的等差数列,则d=
A.2 B.3 C. D.
7.已知双曲线C: 的右焦点为F,O为坐标原点,过点F的直线与双曲线C的两条渐近线分
别交于P,Q两点.点P为线段FQ的中点,且 ,则双曲线C的离心率为
A. B. C.2 D.3
8.已知f(x)是定义在R上的函数,且 , ,则
A.-2 B.-3 C. D.
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题
目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分。9.已知 , ,且 ,则下列不等式恒成立的有
A. B. C. D.
10.如图,菱形ABCD的边长为2, ,E为边AB的中点.将△ADE沿DE折起,折叠后点A
的对应点为A′,使得 ,连接A′B,A′C,则下列说法正确的是
A.D到平面A′BC的距离为 B.四面体A′-CDE的外接球表面积为8π
C.BC与A′D所成角的余弦值为 D.直线A′B与平面A′CD所成角的正弦值为
11.已知函数f(x)为R上的奇函数,当 时, ,且f(x)的图象关
于点(1,1)中心对称,则下列说法正确的是
A. B.直线 与f(x)图象有8个交点
C. 是周期为2的周期函数 D.方程 所有根的和为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知等差数列 , ,则 ________.
13.已知集合 , ,且 的非空子集的个数
为3,则整数b的一个可能取值为________.
14.已知函数 ,若 恒成立,则a的取值范围是________.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.(13分)在△ABC中,角A,B,C所对的边分别为a,b,c,△ABC的周长为18,b,c,a成递增的等差数列, .点D,E和F分别在BC,AC和AB上,满足 ,
, .
(1)求a,b,c的值;
(2)求证:AD,BE和CF三线交于一点K.
16.(15分)如图,在四棱锥P-ABCD中, , , ,
, ,点E是PC的中点.
(1)证明: ;
(2)当 时,求二面角P-BC-A的余弦值.
17.(15分)城市活力是城市高质量发展的关键表征,其反映了城市空间治理能力现代化的水平.城市活
力由人群活动和实体环境两方面构成,通过数学建模研究表明:一天中,区域的居民活动类型(工作、学
习和休闲)越丰富,活动地点总数越多,区域之间人口流动越频繁,城市活力度越高.Q市基于大数据测
算城市活力度,发现该市一工作日中活力度与时间的关系可以用函数
来近似刻画,其中正午12点的城市活力度为20,是工作日内活力度
的最高值;24点到次日早上6点期间的城市活力度均为工作日内活力度的最低值.
(1)分别求m,n的值;
(2)求该工作日内,Q市活力度不大于10的总时长.
18.(17分)已知函数 ,其中 , 是自然对数的底数,f(x)是g
(x)的导函数.
(1)当 时,求曲线 在点(1,g(1))处的切线方程;
(2)当f(x)存在极值时,证明:f(x)的极值小于或等于1.19.(17分)记数列 的前n项和为 ,已知 .
(1)求 的通项公式;
(2)记数列 的前n项和为 .
(ⅰ)求 ;
(ⅱ)证明: .
东北三省精准教学 2024 年 12 月高三联考数学
参考答案及解析
1.【答案】C
【解析】 , .
故选:C.
2.【答案】A
【解析】因为 ,所以 ,即 , ,则 .当 时,
, , ,则 .故“ ”是“ ”的充分不必
要条件.
故选:A.
3.【答案】B
【解析】由 可得 ,解得 ,故 ,故
.
故选:B.
4.【答案】D
【解析】由图易知 , ,得 .
因为 , ,所以 .因为点 在曲线上,所以 ,所以 ,又 ,
所以 , ,所以函数f(x)图象的对称轴应满足 ,得
, ,故直线 不是f(x)图象的一条对称轴,选项A错误;
由 ,得 , ,函数f(x)图象的对称中心为 , ,选项
B错误;
由 , ,得 , ,当 时,
,选项C错误;
将f(x)的图象向左平移 个单位长度后得 ,平移后的函数是偶函
数,选项D正确.
故选:D.
5.【答案】B
【解析】在正四棱台ABCD-A′B′C′D′中, , , ,可得在侧面ABB′A′中,
,故 ,
.
故选:B.
6.【答案】B
【解析】因为 ,所以当 时, ,两式相减得 ,即,所以公比为2, ,又当 时, ,得 ,所以等比数列 的通项
公式为 , ,所以 , ,公差为 .
故选:B.
7.【答案】C
【解析】方法一: ,且P为线段FQ的中点, , ,直线FQ的
方程为 ,与渐近线方程 联立,得Q的坐标 ,
,化简可得 即 ,双曲线C的离
心率 .
方法二:因为P为FQ中点, ,所以 ,又直线OP与直线OQ分别为双曲线C
的两条渐近线,得 ,所以 ,故 .
故选:C.
8.【答案】C
【解析】因为 ,所以当 时, ,
又 ,所以 .又由 ,可得 ,
所以 ,
,函数f(x)是以4为周期的函数,所以
.
故选:C.
9.【答案】ABC
【解析】对于A, , 恒成立,选项A正确;
对于B,由基本不等式可得 ,因为 ,所以取不到等号,即 ,选
项B正确;
对于C,由 , ,可得 ,由指数函数性质易得
,选项C正确;
对于D,令 , , ,选项D错误.
故选:ABC.
10.【答案】BCD
【解析】因为菱形ABCD中,E为AB的中点,所以 ,即将△ADE沿DE折起后, ,
,
又 , , ,
所以 ,则EB,ED,EA′两两垂直,
以E为坐标原点,EB,ED,EA′所在直线分别为x轴,y轴,z轴建立空间直角坐标系Exyz,则
A′(0,0,1),B(1,0,0), , , , ,, .
对于A,设平面A′BC的法向量为 , 取 , ,
D到平面A′BC的距离为 ,选项A错误;
对于B,取CE中点F,连接DF, , ,
过F作直线 ,则四面体A′-CDE的外接球球心O在直线l上,设 ,该外接球的半径为
R,由 ,得 ,解得 , ,四面体A′-CDE的外接
球的表面积为 ,选项B正确;
对于C,BC与A′D所成角的余弦值为 ,选项C正确;
对于D,设平面A′CD的法向量为 ,
取 , , ,选项D正确.
故选:BCD.
11.【答案】ACD
【解析】对于A,f(x)的图象关于点(1,1)中心对称, ,当 时,
,可得 ,又 , ,选项A正确;
对于B,因为f(x)为R上的奇函数,且(0,0)为直线 与f(x)图象的一个交点,所以直线
与f(x)图象交点为奇数个,选项B错误;
对于C,由f(x)的图象关于点(1,1)中心对称,, , ,
,所以 是周期为2的周期函数,选项
C正确;
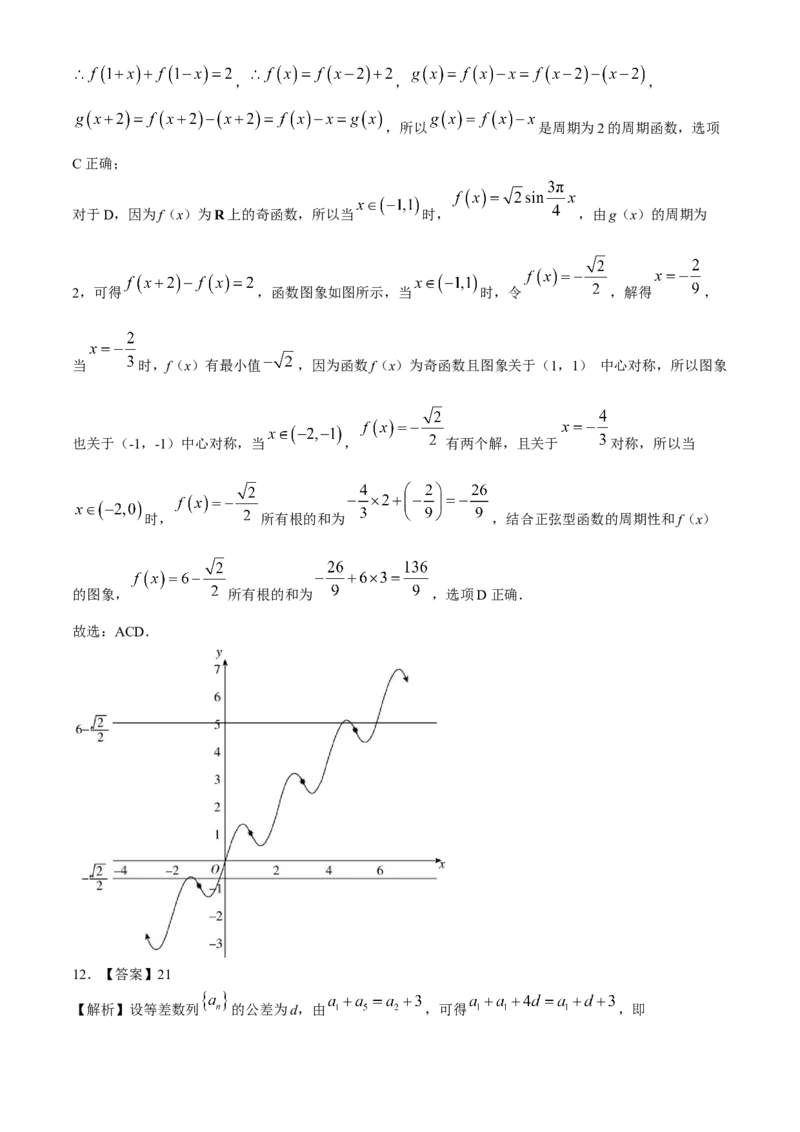
对于D,因为f(x)为R上的奇函数,所以当 时, ,由g(x)的周期为
2,可得 ,函数图象如图所示,当 时,令 ,解得 ,
当 时,f(x)有最小值 ,因为函数f(x)为奇函数且图象关于(1,1) 中心对称,所以图象
也关于(-1,-1)中心对称,当 , 有两个解,且关于 对称,所以当
时, 所有根的和为 ,结合正弦型函数的周期性和f(x)
的图象, 所有根的和为 ,选项D正确.
故选:ACD.
12.【答案】21
【解析】设等差数列 的公差为d,由 ,可得 ,即, .
故答案为:21.
13.【答案】-5/-6/-7(写出一个即可得满分)
【解析】由 可知其图象是以原点为圆心,以5为半径的右半圆(含(0,±5)),如图,
,
的非空子集的个数为3等价于直线 与半圆有2个公共点,当直线经过点(0,-5)时,
,当直线与半圆相切时,可得 ,解得 或 (舍),故 .
故整数b的可能取值为-5,-6,-7.
故答案为:-5/-6/-7(写出一个即可得满分).
14.【答案】(0,1)
【解析】由题意,得 , 恒成立即 , 恒成立.
, 恒成立,化简可得 , ,
, ,
令 , ,故g(x)单调递增,
, ,令 , ,
当 时, ,当 时, , 时,h(x)取最大值 ,
,即 .
故答案为:(0,1).15.【答案】(1) , , (6分) (2)证明见解析(7 分)
【解析】(1)因为△ABC的周长为18,所以 ,
由于b,c,a是递增的等差数列,故 ,
所以 , ①,
又 ②,
由①②,解得 , , .
(备注:推导出①得3分,否则按考点给分;推导出②得1分;联立①②得出a,b,c得2分)
(2)由题意可得 , , ,
所以 , ,
设BE和CF交于点K,由B,K,E三点共线,得 ,
由C,K,F三点共线,得 ,
所以 解得
所以 ,
又 ,所以 ,
所以AD过点K,即AD,BE和CF三线交于一点K.
(备注:按考点给分,漏步骤相应扣分;可使用建系方法解题,过程酌情给分)
16.【答案】(1)证明见解析(6分) (2) (9分)
【解析】(1)由勾股定理, ,满足 ,所以 .
因为 , , , ,
所以 ,
又 ,所以 .
因为 ,且 ,所以 .
(备注:证明 得2分,证明 得3分,证明 得1分)
(2)方法一:取AD的中点O,作 交BC于M,连接OP,则 ,
因为 , , ,所以
,以O为原点,OA,OM,OP 所在直线分别为x轴,y轴,z轴建立空间直角坐标系
Oxyz,
所以A(1,0,0),P(0,0,1), , ,设B(a,b,0), ,
,
则 , , , .
易知平面PAD的一个法向量为 ,因为 ,
所以 ,解得 .
因为 ,所以 ,解得 或 (舍),即 .
设平面PBC的一个法向量为 ,
则 令 ,得 , ,可得 ,
易知平面ABC的一个法向量 ,则 ,
因为二面角P-BC-A为锐二面角,所以二面角P-BC-A的余弦值为 .
(备注:建系给1分,写出点的坐标给1分,计算出平面PBC的法向量给4分,求出二面角的余弦值给3
分,过程酌情给分)
方法二:取AD的中点O,连接OP和OC,再取OC的中点Q,连接QE,
在平面ABCD内过点Q作BC的垂线,垂足为点N,连接EN,
因为 ,且O是AD的中点,所以 .
又 , , ,
所以 .
因为EQ是△POC的中位线,则 ,
所以 .
因为 ,所以 .
因为 , ,且 ,
所以 .又 ,所以 ,
由二面角的平面角的定义可知,∠ENQ即为二面角P-BC-A的平面角.
连接BQ,并延长BQ交CD于点T.
由 , , ,所以 .
当 时, ,且 ,
所以 .
由平面与平面平行的性质定理可知 .
记AC交BT于F,因为点Q是OC的中点, ,所以F是AC的中点,
由此可知 , ,因为 ,所以 ,且 .
由 ,可知 ,
由 得 ,所以 ,
,因此 ,
,
所以二面角P-BC-A的余弦值为 .
(备注:分析出∠ENQ为二面角给3分,分析出 给2分,计算出∠ENQ的余弦值给3分,过程
酌情给分)
17.【答案】(1) , (6分) (2)14小时(9分)
【解析】(1)由正午12点的城市活力度为20,知 ,
代入数据得 ,解得 ,
24点到次日早上6点期间的城市活力度均为工作日内活力度的最低值,
故 ,代入数据得 ,解得 .
(2)由(1)知
当 时,令 ,解得 ,
当 时,令 ,则 ,, ,
解得 ,故一日内只有 时活力度大于10,
即该工作日内有14个小时活力度不大于10.
(备注:(1)问求得m给3分,求得n给3分;(2)问求出 给2分,求出 给5分,
答案给2分)
18.【答案】(1) (6分) (2)证明见解析(11分)
【解析】(1)对g(x)求导可得 ,当 时, ,
故 , ,
故曲线 在点(1,g(1))处的切线方程为 ,
化简得 .
(备注:求导给1分,求出切线方程给3分,化简给2分)
(2)由第(1)问得 ,求导得 ,
当 时,f(x)单调递增,故f(x)不存在极值,
当 时,存在 ,使得 ,且 ,
此时在 上, ,f(x)单调递减,在 上, ,f(x)单调递增,此时f
(x)存在极值 ,
由计算得 ,
设 , ,则 ,
当 时, , ,
当 时, ,所以当 时,h(a)取得最大值,
故 ,即f(x)的极值小于或等于1.
(备注:讨论极值 存在情况得5分,未讨论扣2分;构造函数给1分,求最大值给3分,答案给1
分)
19.【答案】(1) , (7分) (2)(ⅰ) ,
(7分);(ⅱ)证明见解析(3分)
【解析】(1)当 时, ,解得 ,
当 时, ,所以 ,
即 , 是首项和公比均为2的等比数列, , .
(备注:求 时 的值得2分,求出公比得2分,写出 的通项公式得3分)
(2)方法一:(ⅰ)由 ,
得 ,
故 .
(ⅱ)因为 ,故 .
(备注:(ⅰ)三角恒等变换拆分给2分,移项构造裂项相消得到 给5分;(ⅱ)证明给3分)
方法二:(ⅰ)设数列 的通项公式为 ,则 ,
当n为6的倍数时,
当n除6余1时, ,
当n除6余2时, ,当n除6余3时, ,
当n除6余4时, ,
当n除6余5时, ,
综上所述:
(ⅱ)
(备注:过程酌情给分)