文档内容
高三期初考数学
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 已知集合 , ,则 ( )
A. B.
C. D.
【答案】A
【解析】
【分析】化简集合,由交集的概念即可求解.
【详解】因为 ,
所以 .
故选:A.
2. 若 ,则 ( )
A. B. C. D.
【答案】C
【解析】
【分析】由复数四则运算以及共轭复数的概念即可得解.
【详解】因为 ,所以 .
故选:C.
3. 已知向量 , 满足 , ,则 ( )
A. B. 2 C. D. 4
【答案】A
【解析】
【分析】由向量数量积公式计算即可得.
【详解】因为 , ,所以 .
第1页/共21页
学科网(北京)股份有限公司故选:A.
4. 已知椭圆 的上焦点为 ,则 ( )
A. B. 5 C. D. 7
【答案】C
【解析】
【分析】由焦点概念以及平方关系即可求解.
【详解】因为椭圆的焦点在 轴上,所以 , .
因为 ,所以 ,所以 .
故选:C.
5. 设函数 且 在区间 上单调递增,则 的取值范围是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据单调性与导数的关系可得 在 上恒成立,进而即可求解.
【详解】依题意, 在 上恒成立,
记 ,则 在 上恒成立,
在 上单调递增,所以只需 ,解得 ,
故选:A.
6. 第19届亚运会在杭州举行,为了弘扬“奉献,友爱,互助,进步”的志愿服务精神,5名大学生将前往
3个场馆 开展志愿服务工作.若要求每个场馆都要有志愿者,则当甲不去场馆 时,场馆 仅有2
名志愿者的概率为( )
第2页/共21页
学科网(北京)股份有限公司A. B. C. D.
【答案】B
【解析】
【分析】首先得甲去场馆 或 的总数为 ,进一步由组合数排列数即可得所求概率.
【详解】不考虑甲是否去场馆 ,所有志愿者分配方案总数为 ,
甲去场馆 的概率相等,所以甲去场馆 或 的总数为 ,
甲不去场馆 ,分两种情况讨论,
情形一,甲去场馆 ,场馆 有两名志愿者共有 种;
情形二,甲去场馆 ,场馆 场馆 均有两人共有 种,
场馆 场馆 均有两人共有 种,所以甲不去场馆 时,
场馆 仅有2名志愿者的概率为 .
故选:B.
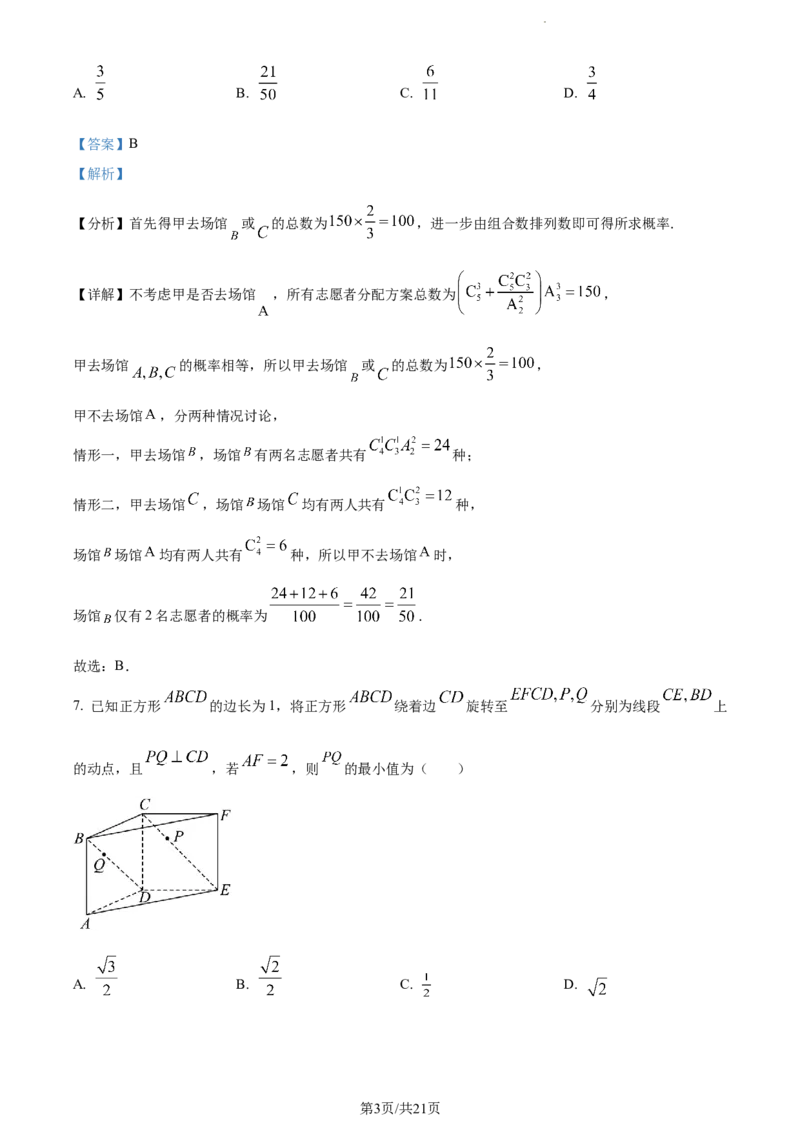
7. 已知正方形 的边长为1,将正方形 绕着边 旋转至 分别为线段 上
的动点,且 ,若 ,则 的最小值为( )
A. B. C. D.
第3页/共21页
学科网(北京)股份有限公司【答案】A
【解析】
【分析】根据线线垂直可证明线面垂直,进而根据余弦定理求解 ,结合二次函数的性质即
可求解.
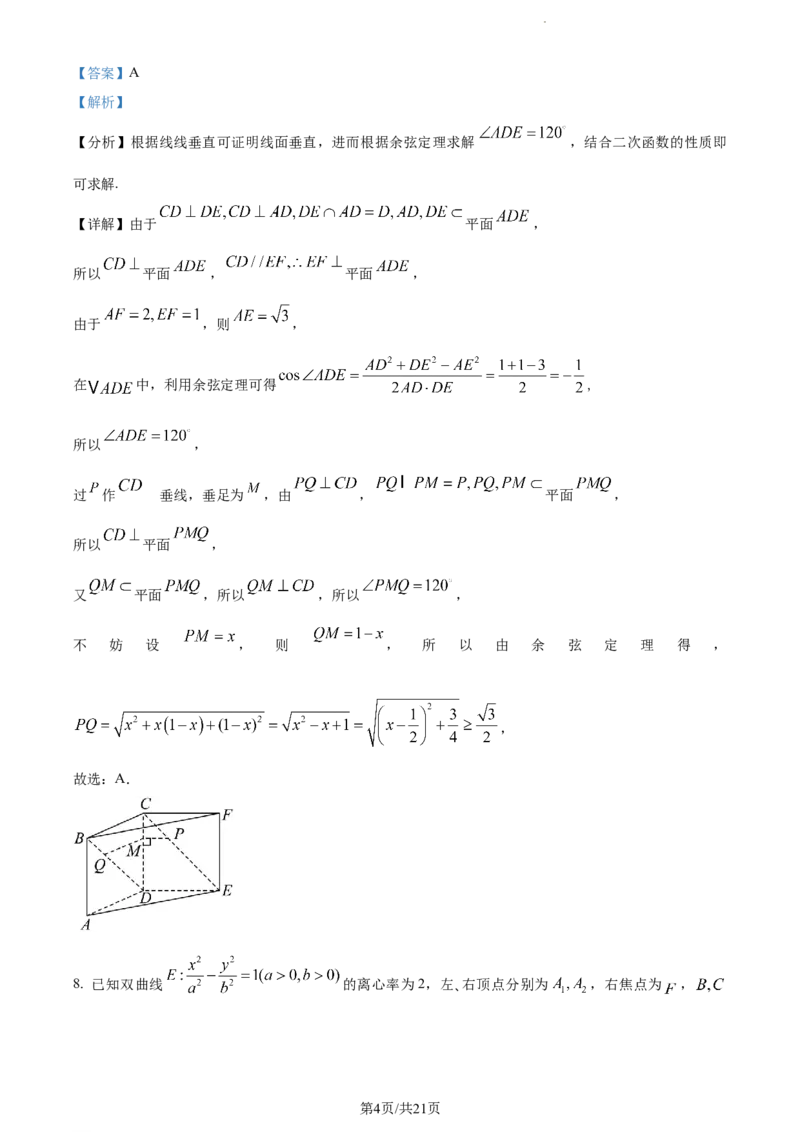
【详解】由于 平面 ,
所以 平面 , 平面 ,
由于 ,则 ,
在 中,利用余弦定理可得 ,
所以 ,
的
过 作 垂线,垂足为 ,由 , 平面 ,
所以 平面 ,
又 平面 ,所以 ,所以 ,
不 妨 设 , 则 , 所 以 由 余 弦 定 理 得 ,
,
故选:A.
8. 已知双曲线 的离心率为2,左、右顶点分别为 ,右焦点为 ,
第4页/共21页
学科网(北京)股份有限公司是 上位于第一象限的两点, ,若 ,则 ( )
A. B. C. D.
【答案】D
【解析】
【分析】由题意 , ,余弦定理得 ,得 ,由
,求 ,最后由 求值即可.
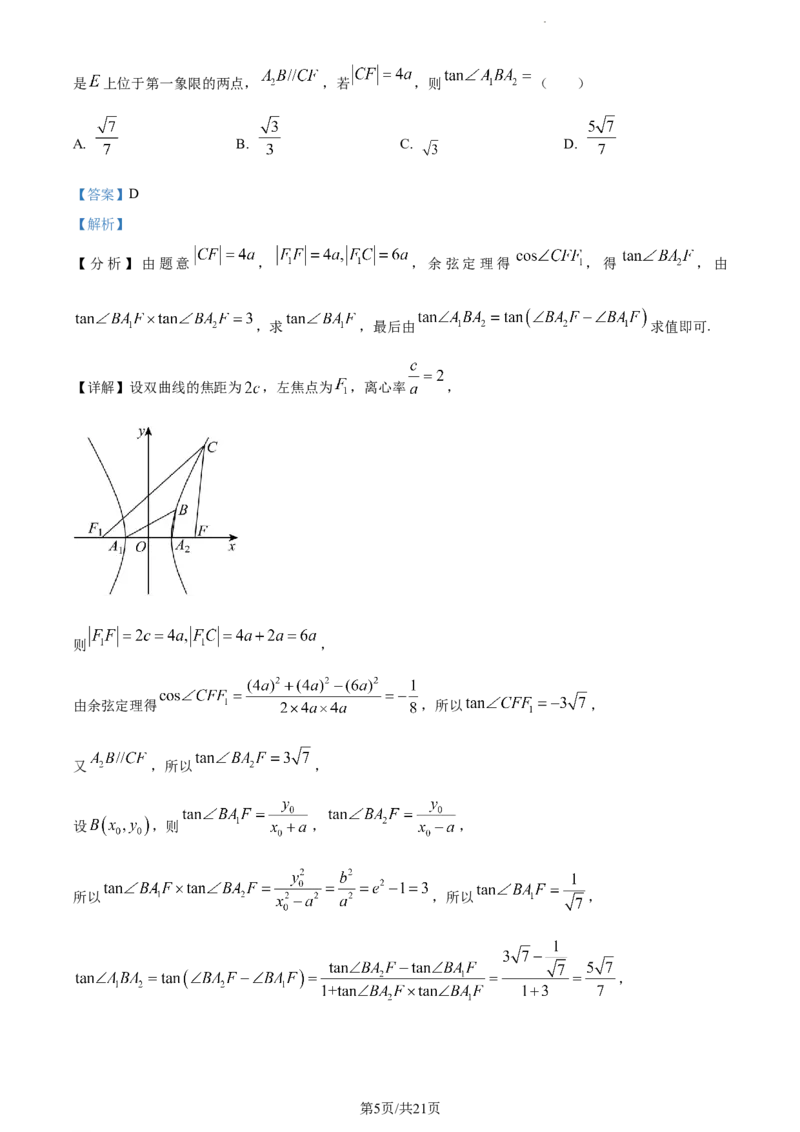
【详解】设双曲线的焦距为 ,左焦点为 ,离心率 ,
则 ,
由余弦定理得 ,所以 ,
又 ,所以 ,
设 ,则 , ,
所以 ,所以 ,
,
第5页/共21页
学科网(北京)股份有限公司故选:D.
【点睛】思路点睛:
双曲线与焦点三角形有关的计算或证明常利用正弦定理余弦定理和 , 中利用余弦
定理得 ,可求得 ,点 坐标满足双曲线方程,可得 ,
可求 ,利用 计算即可.
二、多选题(每题5分,少选得2分,错选0分)
9. 下列等式中正确的是( )
A. B.
C. D.
【答案】AB
【解析】
【分析】根据题意结合三角恒等变换逐项分析判断.
【详解】对于选项A: ,故A正确;
对于选项B: ,故B正确;
对于选项C: ,故C错误;
对于选项D: ,故D错误;
故选:AB.
10. 已知 ,若 ,则( )
A. B.
第6页/共21页
学科网(北京)股份有限公司C. 的最大值为 D. 的最小值为8
【答案】ABD
【解析】
【分析】对于AB:根据题意消去 ,结合 的取值范围分析求解;对于C:根据基本不等式运算求解;对
于D:根据“1”的灵活应用结合基本不等式分析求解.
【详解】因为 , ,则 ,可得 ,
对于选项AB:因为 ,
所以 , ,故AB正确;
对于选项C:因为 ,
当且仅当 时,等号成立,
所以 的最大值为 ,故C错误;
对于选项D:因为 ,
当且仅当 ,即 时,等号成立,
所以 的最小值为8,故D正确;
故选:ABD.
11. 已知双曲线 的渐近线方程为 ,则下列结论正确的是( )
第7页/共21页
学科网(北京)股份有限公司A. B. 的离心率为
C. 曲线 经过 的一个顶点 D. 与 有相同的渐近线
【答案】ACD
【解析】
【分析】根据双曲线的渐近线方程求出 即可判断A;根据双曲线的离心率公式即可判断B;求出双曲线
的顶点即可判断C;求出双曲线 的渐近线方程即可判断D.
【详解】双曲线 的渐近线方程为 ,
所以 ,解得 ( 舍去),故A正确;
双曲线 ,
所以 的离心率为 ,故B错误;
双曲线 的顶点为 ,
因为 ,所以曲线 经过 的一个顶点 ,故C正确;
对于D,令 ,则 ,
即 的渐近线方程为 ,故D正确.
故选:ACD.
12. 已知数列 ,下列结论正确的有( )
第8页/共21页
学科网(北京)股份有限公司A. 若 , ,则
B. 若 , ,则
C. 若 ,则数列 是等比数列
D. 若 为等差数列 的前 项和,则数列 为等差数列
【答案】ABD
【解析】
【分析】直接利用累加法可判断选项A项;构造 为等比数列可判断B项;利用 与 的关系可求
得 通项公式即可判断C项;利用等差数列的前n项和公式及定义法判断等差数列即可判断D项.
【详解】对于选项A,由 ,得 ,
则
,故A项正确;
对于选项B,由 得 ,
所以 为等比数列,首项为 ,公比为2,
所以 ,所以 ,故B项正确;
对于选项C,因为 ,
当 时, ,
当 时, ,
第9页/共21页
学科网(北京)股份有限公司将 代入 ,得 ,
所以 ,所以数列 不是等比数列,故C项错误.
对于选项D,设等差数列的公差为d,
由等差数列前 项和公式可得 ,
所以 与n无关,
所以数列 为等差数列,故D项正确.
故选:ABD.
三、填空题(每题5分)
13. 已知向量 ,则 在 上的投影向量的坐标为______.
【答案】
【解析】
【分析】根据向量的坐标运算可得 ,进而结合投影向量的定义运算求解.
【详解】由题意可得: ,
所以 在 上的投影向量的坐标为 .
故答案为: .
14. 已知函数 在区间 上的最大值为 ,最小值为 ,则
______.
第10页/共21页
学科网(北京)股份有限公司【答案】6
【解析】
【分析】设 ,分析可知 为奇函数,根据奇函数的对称性分析求解.
【详解】设 ,
则 的定义域为 ,且连续不断,
由 ,可知 为奇函数,
设 在 上的最大值为 ,
由奇函数的对称性可知 在 上的最小值为 ,
则函数 在区间 上的最大值为 ,最小值为 ,
所以 .
故答案为:6.
15. 若函数 的定义域为 ,则函数 的定义域为__________.
【答案】
【解析】
【分析】首先得 的定义域为 ,进一步列不等式组即可得解.
【详解】因为 ,所以 ,所以 的定义域为 ,
要使 有意义,需满足 ,解得 ,
所以函数 定义域为 .
的
第11页/共21页
学科网(北京)股份有限公司故答案为: .
16. 已知椭圆 为 的左、右焦点, 为 上的一个动点(异于左右顶点),设
的外接圆面积为 ,内切圆面积为 ,则 的最小值为__________.
【答案】
【解析】
【分析】当 为短轴端点时, 最大,进而求出 的范围,由正弦定理得外接圆的半径
,再利用余弦定理和三角形面积公式化简得到 的面积 ,由三角形内切圆的
半径公式可得 的内切圆半径 ,化简可得 ,利用基本不
等式求出最值即可.
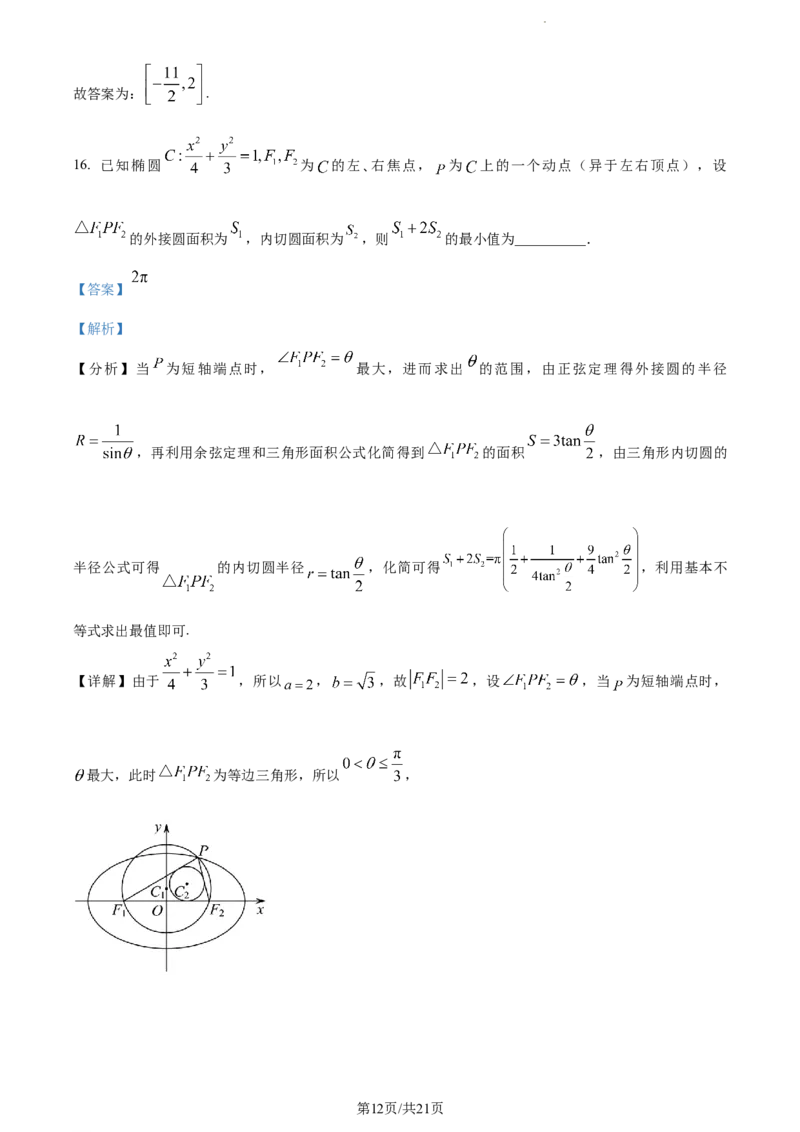
【详解】由于 ,所以 , ,故 ,设 ,当 为短轴端点时,
最大,此时 为等边三角形,所以 ,
第12页/共21页
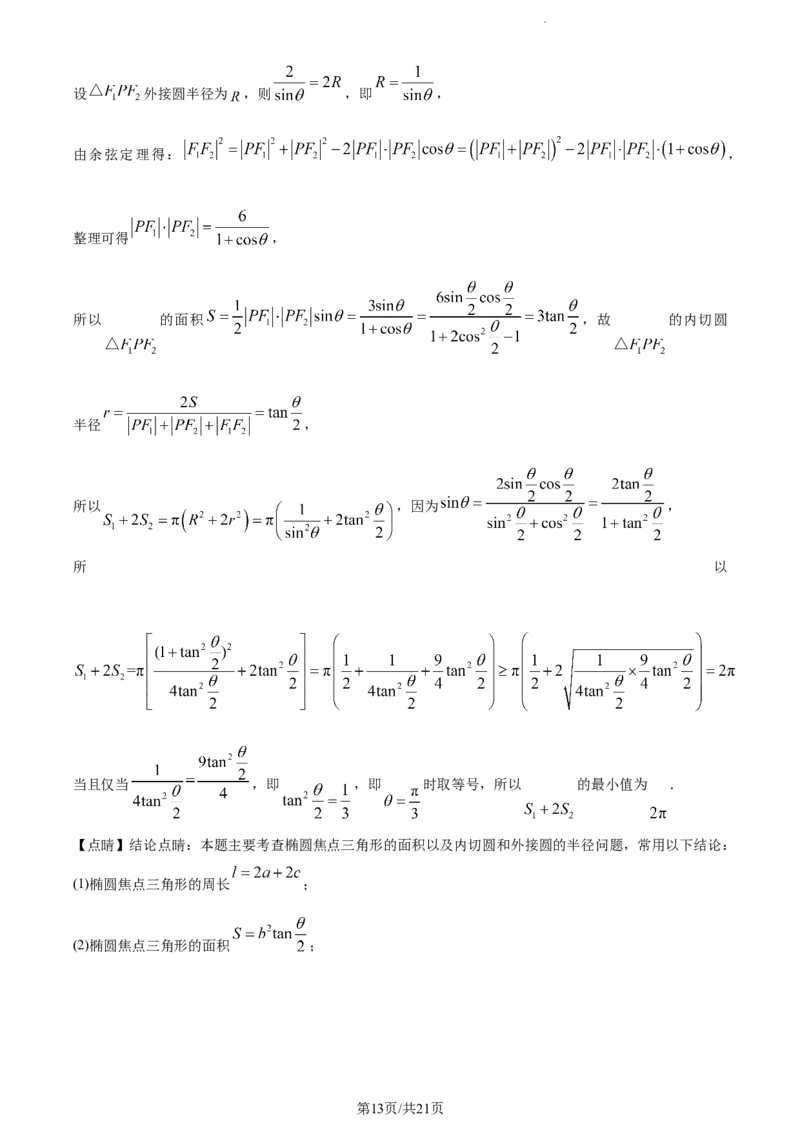
学科网(北京)股份有限公司设 外接圆半径为 ,则 ,即 ,
由余弦定理得: ,
整理可得 ,
所以 的面积 ,故 的内切圆
半径 ,
所以 ,因为 ,
所 以
当且仅当 ,即 ,即 时取等号,所以 的最小值为 .
【点睛】结论点睛:本题主要考查椭圆焦点三角形的面积以及内切圆和外接圆的半径问题,常用以下结论:
(1)椭圆焦点三角形的周长 ;
(2)椭圆焦点三角形的面积 ;
第13页/共21页
学科网(北京)股份有限公司(3)三角形外接圆的半径公式: ;
(4)三角形内切圆的半径公式: (其中 为三角形面积, 为周长)
四、解答题
17. 已知集合 , .
(1)若 ,求实数 的取值范围;
(2)若 ,求实数 的取值范围.
【答案】(1)
(2) .
【解析】
【分析】(1)依题意可得 ,即可得到不等式组,解得即可;
(2)依题意可得 或 ,即可求出参数的取值范围.
【小问1详解】
解:因为 ,所以 ,
所以 ,即 ;
【小问2详解】
解:因为 ,
所以 或 ,
所以 .
18. 已知向量 , ,设函数 .
(1)求 的最小正周期;
第14页/共21页
学科网(北京)股份有限公司(2)当 时,求函数 的最小值.
【答案】(1)
(2)
【解析】
【分析】(1)结合向量数量积的坐标运算求出 ,即可得出最小正周期;
(2) 时,可得 ,根据函数的图象和性质即可求出结果.
【小问1详解】
由向量 , ,
可得
,
所以函数 的最小正周期为 .
【小问2详解】
由(1)知 ,
当 时,可得 ,
所以当 时,即 ,函数 的最小值为 .
19. 2021年秋全国中小学实行“双减政策”和“5+2”模式.为响应这一政策,某校开设了“篮球”“围棋”等课后
延时服务课程.甲、乙两位同学在学习围棋后,切磋围棋棋艺.已知甲先手时.甲获胜的概率为 ,乙先
第15页/共21页
学科网(北京)股份有限公司手时,乙获胜的概率为 ,每局无平局,且每局比赛的胜负相互独立,第一局甲先手.
(1)若每局负者下一局先手,两人连下3局,求乙至少胜两局的概率;
(2)若每局甲都先手,胜者得1分,负者得0分,先得3分者获胜且比赛结束,比赛结束时,负者的积分
为 ,求 的分布列与数学期望.
【答案】(1)
(2)分布列见解析,
【解析】
【分析】(1)根据相互独立事件及互斥事件的概率公式计算可得;
(2)依题意可得 的所有可能结果为 、 、 ,求出所对应的概率,即可得到分布列与数学期望;
【小问1详解】
解:设事件 为乙至少胜两局,则乙有负胜胜,胜负胜,胜胜负,胜胜胜四种情况,
所以 ;
【小问2详解】
解:依题意可得 的所有可能结果为 、 、 ,
则 , ,
,
所以 的分布列为
第16页/共21页
学科网(北京)股份有限公司所以 ;
20. 设 为数列 的前 项和,已知 为等比数列,且 .
(1)求数列 通项公式;
的
(2)已知 ,设 ,记 为数列 的前 项和,证明: .
【答案】(1)
(2)证明见解析
【解析】
【分析】(1)由 ,得 ,等比数列 的首项为1公比为2,可得通项;
(2)由 与 的关系,求出 的通项,通过放缩法证明不等式.
【小问1详解】
为数列 的前 项和, ,
则有 ,所以 ,等比数列 的公比为2,
又 ,所以 ;
【小问2详解】
证明:由(1)知, ,当 时, ,
所以 ,所以 ,
第17页/共21页
学科网(北京)股份有限公司则 ,
因此 .
21. 已知正项数列 是公差为2的等差数列,且 成等比数列.
(1)求数列 的通项公式;
(2)求数列 的前 项和 .
【答案】(1) ;(2)
【解析】
【详解】分析:(1)利用已知条件可列出 的两个方程,联立 ,解出 ,从而再由
是等差数列得通项公式;
(2)数列 的前 项和可用错位相减法求得.
详解:(1)因为数列 是公差为2的等差数列,所以 ,
则 ,
又 成等比数列,所以 ,
解得 或 ,因为数列 为正项数列,所以 .
所以 ,
第18页/共21页
学科网(北京)股份有限公司故 .
(2)由(1)得 ,
所以 ,
所以 ,
即 ,
故 .
点睛:解决数列求和问题首先要掌握等差数列和等比数列的前 项和公式,其次要掌握一些特殊数列的求
和方法,设 是等差数列, 是等比数列,则数列 用分组求和法求和,数列 用错位
相减法求和,数列 用裂项相消法求和.
22. 已知函数 .
(1)当 时,求 的单调区间;
(2)若 是 的极小值点,求 的取值范围.
【答案】(1) 在 上单调递减
(2)
【解析】
【分析】(1)求导,构造函数 ,利用导数求解单调性即可求解,
(2) 求导,结合分类讨论求解函数的单调性,即可结合极值点的定义求解.
【小问1详解】
当 时, ,
第19页/共21页
学科网(北京)股份有限公司设 ,则 ,
所以当 时, 单调递增,
当 时, 单调递减,
当 时, 取得极大值 ,所以 ,
所以 在 上单调递减;
【小问2详解】
,
设 ,则 ,
(i)当 时,二次函数 开口向上,对称轴为 ,
当 时, 单调递增,
因为 ,所以当 时, 单调递减,
当 时, 单调递增,所以 是 的极小值点.
当 时, ,又 ,
所以存在 ,使得 ,所以当 时, 单调递增,
又 ,所以当 时, 单调递减,
当 时, 单调递增,所以 是 的极小值点;
(ii)当 时, ,当 时, 单调递减,
第20页/共21页
学科网(北京)股份有限公司当 时, , 单调递增,所以 是 的极小值点;
(iii)当 时, 开口向下,对称轴为 ,
此时 ,故 ,使 ,
当 时, ,因此 在 上单调递增,
又 ,当 时, 单调递减,
当 时, 单调递增,所以 为 的极小值点;
(iv)当 时, ,使 ,
当 时, ,因此 在 上单调递减,
又 ,当 时, 单调递增,
当 时, 单调递减,所以 为 的极大值点;
(v)当 时,由(1)知 非极小值点.
综上所述, .
【点睛】方法点睛:本题考查了导数的综合运用,利用导数求单调性时,如果求导后的正负不容易辨别,
往往可以将导函数的一部分抽离出来,构造新的函数,利用导数研究其单调性,进而可判断原函数的单调
性.
第21页/共21页
学科网(北京)股份有限公司