文档内容
广东省东莞市2024-2025 学年高二下学期七校联考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知函数 在 处可导,且 ,则 ( )
A. B. C. D.2
2.函数 的单调减区间是( )
A. B. C. D.
3. 的展开式的常数项为( )
A.210 B.252
C. D.
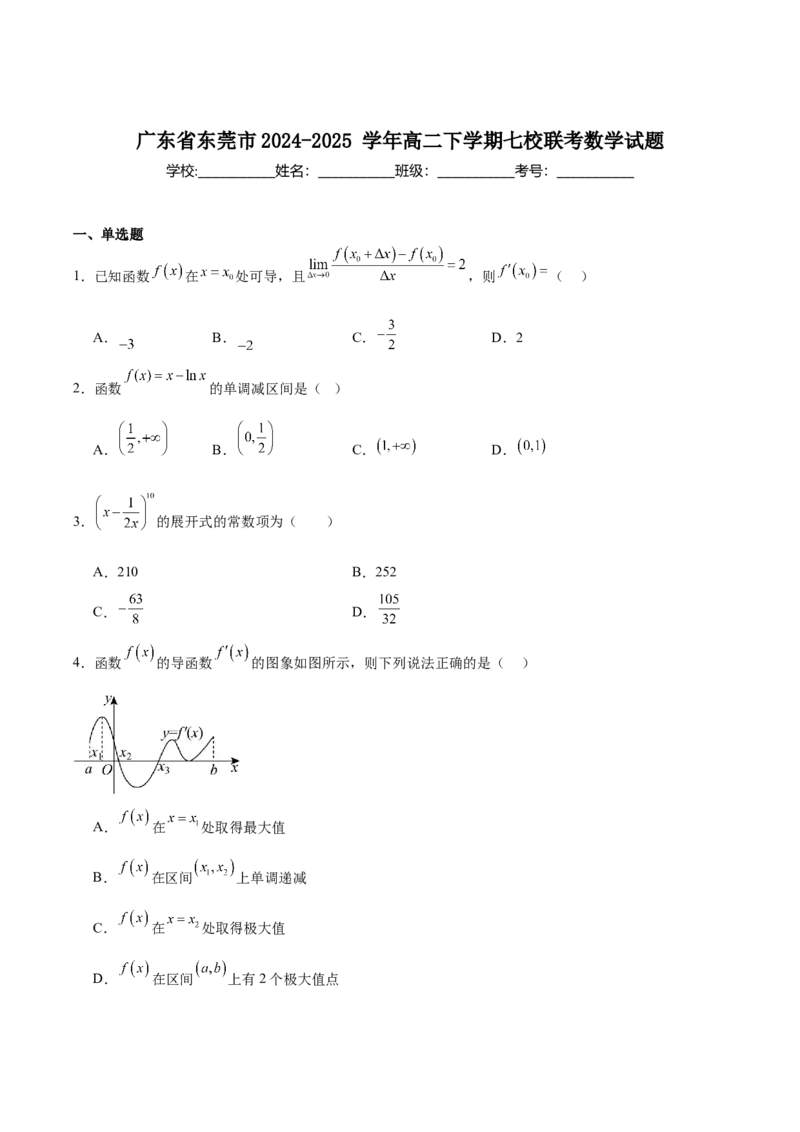
4.函数 的导函数 的图象如图所示,则下列说法正确的是( )
A. 在 处取得最大值
B. 在区间 上单调递减
C. 在 处取得极大值
D. 在区间 上有2个极大值点5.函数 在 上的最小值为( )
A. B. C. D.1
6.设随机变量 ,若 ,则 ( )
A.60 B.56 C.12 D.8
7.甲,乙两人进行乒乓球比赛,比赛采用3局2胜制,如果每局比赛甲获胜的概率为0.7,乙获胜的概率
为0.3,且各局比赛结果相互独立,那么在甲获胜的条件下,比赛进行了3局的概率为( )
A. B. C. D.
8.过点 可以做三条直线与曲线 相切,则实数 的取值范围是( )
A. B. C. D.
二、多选题
9.甲,乙,丙,丁,戊五人并排站成一排,下列说法正确的是( )
A.如果甲,乙必须相邻且乙在甲的右边,那么不同的排法有24种
B.最左端只能排甲或乙,最右端不能排甲,则不同的排法共有42种
C.甲乙不相邻的排法种数为82种
D.甲乙丙按从左到右的顺序排列的排法有20种
10.已知 (常数 )的展开式中第5项与第7项的二项式系数相等,则( )
A.
B.展开式中奇数项的二项式系数的和为256
C.展开式中 的系数为
D.若展开式中各项系数的和为1024,则第6项的系数最大
11.若 件产品中有 件次品和 件正品.现从中随机抽取 件产品,记取得的次品数为随机变量 ,则
下列结论正确的是( )A.若是有放回的抽取,则
B.若是无放回的抽取,则
C.若是有放回的抽取, 的数学期望
D.若是无放回的抽取, 的数学期望
三、填空题
12.已知随机变量 ,若 ,则 .
13.若函数 在区间 上单调递增,则实数 的取值范围为 .
14.函数 ,若函数 有2个零点,则a的取值范围 .
四、解答题
15.已知函数 在点 处的切线斜率为4,且在 处取得极值.
(1)求函数 的解析式;
(2)求函数 的单调区间.
16.有 和 两道谜语,张某猜对 谜语的概率为0.8,猜对得奖金10元;猜对 谜语的概率为0.5,猜对
得奖金20元.每次猜谜的结果相互独立.
(1)若张某猜完了这两道谜语,记张某猜对谜语的道数为随机变量 ,求随机变量 的分布列与期望;
(2)现规定:只有在猜对第一道谜语的情况下,才有资格猜第二道.如果猜谜顺序由张某选择,为了获得更多
的奖金,他应该选择先猜哪一道谜语?
17.已知函数 , .
(1)求 的极值;
(2)讨论 的单调性;(3)若 且 时,求证 .
18.在某人工智能的语音识别系统开发中,每次测试语音识别成功的概率受环境条件(安静或嘈杂)的影
响.
(1)已知在安静环境下,语音识别成功的概率为 ;在嘈杂环境下,语音识别成功的概率为0.6. 某天进行
测试,已知当天处于安静环境的概率为0.3,处于嘈杂环境的概率为0.7 .
(i)求测试结果为语音识别成功的概率;
(ii)已知测试结果为语音识别成功,求当天处于安静环境的概率;
(2)已知当前每次测试成功的概率为 ,每次测试成本固定,现有两种测试方案:方案一:测试4次;方
案二:先测试3次,如果这3次中成功次数小于等于2次,则再测试2次,否则不再测试. 为降低测试成本,
以测试次数的期望值大小为决策依据,应选择哪种方案?
19.某大型企业准备把某一型号的零件交给甲工厂或乙工厂生产.经过调研和试生产,质检人员抽样发现:
甲工厂试生产的一批零件的合格品率为80%;乙工厂试生产的另一批零件的合格品率为90%;若将这两批
零件混合放在一起,则合格品率为88%.
(1)设甲工厂试生产的这批零件有m件,乙工厂试生产的这批零件有n件.求证: ;
(2)从混合放在一起的零件中随机抽取3个,用频率估计概率,记这3个零件中来自甲工厂的个数为X,求
X的分布列和数学期望;
(3)为了争取获得该零件的生产订单,甲工厂提高了生产该零件的质量指标.已知在甲工厂提高质量指标的
条件下,该大型企业把零件交给甲工厂生产的概率大于在甲工厂不提高质量指标的条件下,该大型企业把
零件交给甲工厂生产的概率.设事件 “甲工厂提高了生产该零件的质量指标”,事件 “该大型企
业把零件交给甲工厂生产”,已知 ,证明: .广东省东莞市2024-2025 学年高二下学期七校联考数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C C C A C A ABD AD
题号 11
答案 ACD
1.D
【详解】由导数的定义知 .
故选:D.
2.D
【详解】 ,定义域为 , ,
令 ,解得 .
故答案为:D
3.C
【详解】对于二项式 ,根据二项式展开式通项公式得: ,
对 进行化简: ,
令 , 解得 .
将 代入到 中可得:
故选:C.
4.C
【详解】由导函数的图象可知:
0 0 非负
递增 极大值 递减 极小值 递增
故选:C5.C
【详解】 ,令 ,解得 ,令 ,解得 ,
故 在 上单调递减,在 上单调递增,故 .
故选:C.
6.A
【详解】由二项分布的性质得 ,
,
故选:A.
7.C
【详解】设甲获胜为事件A,比赛进行了3局为事件B,
则 , ,
所以 .
故选:C.
8.A
【详解】设切点为 , , ,
点 处的切线斜率 ,
则过点 的切线方程为 ,
又切线过点 ,所以 ,化简得 ,
过点 可以作三条直线与曲线 相切,
方程 有三个不等实根.令 ,求导得到 ,
令 ,解得 , ,
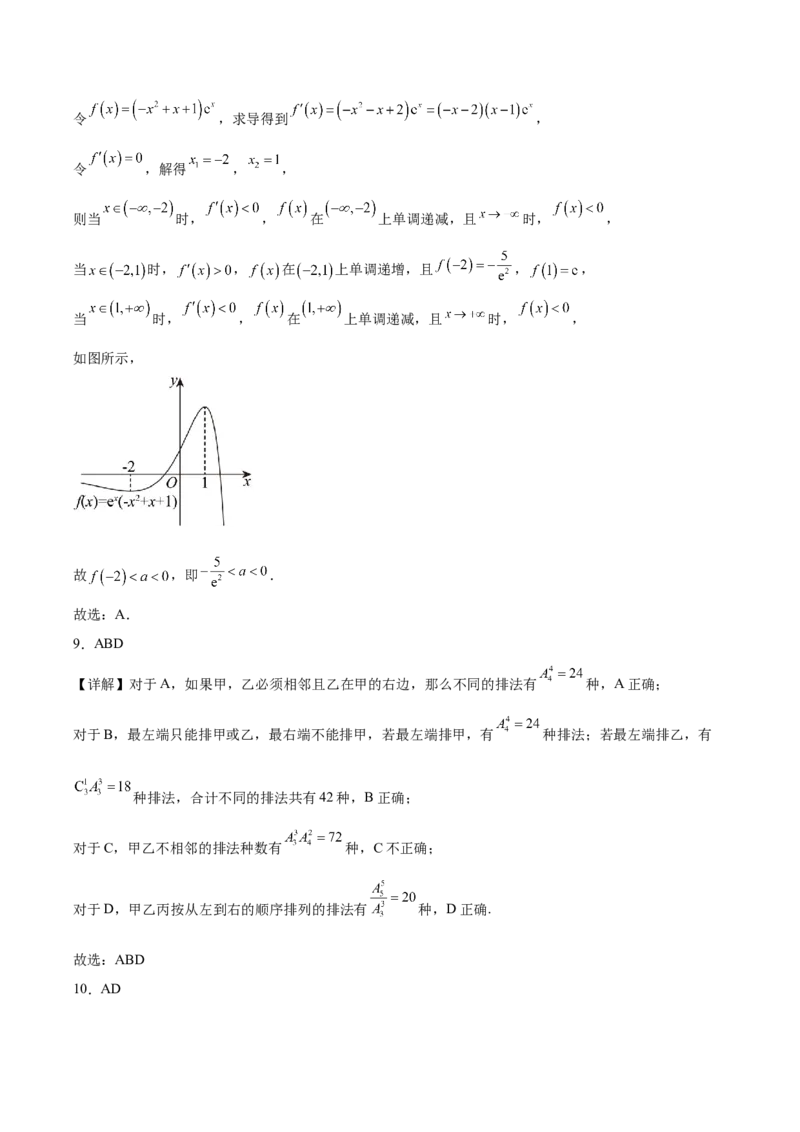
则当 时, , 在 上单调递减,且 时, ,
当 时, , 在 上单调递增,且 , ,
当 时, , 在 上单调递减,且 时, ,
如图所示,
故 ,即 .
故选:A.
9.ABD
【详解】对于A,如果甲,乙必须相邻且乙在甲的右边,那么不同的排法有 种,A正确;
对于B,最左端只能排甲或乙,最右端不能排甲,若最左端排甲,有 种排法;若最左端排乙,有
种排法,合计不同的排法共有42种,B正确;
对于C,甲乙不相邻的排法种数有 种,C不正确;
对于D,甲乙丙按从左到右的顺序排列的排法有 种,D正确.
故选:ABD
10.AD【详解】由 ,则其展开式的通项为 ,
对于A,根据题意可得 ,由组合数的性质可知 ,故A正确;
对于B,由 ,则展开式中奇数项的二项式系数之和为 ,故B错误;
对于C,由 解得 ,则展开式中 的系数为 ,故C错误;
对于D,令 ,则展开式中各项系数之和 ,解得 ,
可得展开式的通项为 ,即每项系数均为该项的二项式系数,
易知展开式中第6项为二项式 的中间项,则其系数最大,故D正确.
故选:AD
11.ACD
【详解】若是有放回的抽取,则 ,
则 ,
,故选项A和C正确,
若是无放回的抽取,则 可能取 , , , ,
又 , ,
, ,
所以 ,故选项B错误,选项D正确,
故选:ACD.
12.0.2【详解】因为 , ,
所以 ,
所以 .
故答案为: .
13.
【详解】由 ,得 ,
因为函数 在区间 上单调递增,
所以 在区间 上恒成立,
即 恒成立,因为 ,所以 ,所以 ,
所以实数 的取值范围为 .
故答案为: .
14.
【详解】函数 的定义域为R,由 ,得 ,
令函数 ,求导得 ,
当 时, 单调递减,当 时, 单调递增,
则 ,又当 时, ;当 时, ,
由函数 有两个零点,得直线 与函数 的图象有两个交点,
在同一坐标系内作出直线 与函数 的图象,如图:观察图象知,当且仅当 时,直线 与函数 的图象有两个交点,
所以 的取值范围是 .
故答案为:
15.(1)
(2)递减区间是 ;增区间是 ,
【详解】(1)解:由函数 ,可得 ,
因为函数 在点 处的切线斜率为 ,且在 处取得极值,
可得 ,即 ,解得解得 ,
所以函数的解析式为 .
(2)解:由函数 ,可得 ,
令 ,得 或 ,
则 的关系,如下表:
0 0↗ 2 ↘ ↗
所以 的单调递减区间是 ,单调递增区间是 , .
16.(1)分布列见解析,
(2)先猜A
【详解】(1)由题意可得, 的可能取值为 ,
,
,
,
则分布列为
则 .
(2)设选择先猜A谜语得到的奖金为 元,选择先猜B谜语得到的奖金为 元,
则随机变量 的可能取值为:0,10,30,
可得 , ,
,
所以随机变量 的的分布列为:
1 3
Y 0
0 0
0. 0. 0.
P
2 4 4
所以期望 ;
又由随机变量 的可能取值为:0,20,30,可得 , , ,
随机变量 的分布列为:
2 3
Z 0
0 0
0. 0. 0.
P
5 1 4
所以期望为 ,
∴ ,所以小明应该先猜A.
17.(1)极小值 ,无极大值
(2)答案见解析
(3)证明见解析
【详解】(1)函数 的定义域为 ,求导得 ,
时, , 时, ,
所以函数 在 处取得极小值 ,无极大值.
(2)函数 的定义域为 ,求导得 ,
当 时, 恒成立,函数 在 上单调递增;
当 时,由 ,得 ;由 ,得 ,
函数 在 上单调递减,在 上单调递增,
所以当 时,函数 在 上单调递增,
当 时,函数 在 上单调递减,在 上单调递增.
(3)当 时, ,不等式 ,
令函数 ,求导得 ,令 ,求导得 ,函数 在 上单调递增,
而 ,则存在 ,使 ,即 ,
此时 , ,当 时, ,当 时, ,
函数 在 上单调递减,在 上单调递增,
因此 ,
所以当 时, .
18.(1)(i) ;(ii)
(2)方案一
【详解】(1)记事件 =“某天进行测试时处于安静环境”, =“某天进行测试时处丁嘈杂环境”,事件
=“测试结果语音识别成功”.
根据题意得
(i)由全概率公式得
(ii)“已知测试结果语音识别成功,当天处于安静环境的概率”,就是在事件 发生的条件下 发生的
概率,
即
(2)方案一的测试次数的数学期望为4.
用 表示“方案二测试的次数”,由题意得 的可能取值为3,5.
则所以方案二测试次数的数学期望为 .
又因为 ,
所以以测试次数的期望值大小为决策依据,应选择方案一.
19.(1)证明见解析
(2)分布列见解析,
(3)证明见解析
【详解】(1)甲工厂试生产的一批零件的合格品率为80%,共 件,则合格件数为 ,
乙工厂试生产的一批零件的合格品率为90%,共 件,则合格件数为 ,
混合后,总零件数为 ,合格品率为88%,则混合后合格零件数为 ,
则 ,化简可得 ,即 .
(2)设甲工厂试生产的这批零件有 件,乙工厂试生产的这批零件有 件,
事件 “混合放在一起零件来自甲工厂”;
事件 “混合放在一起零件来自乙工厂”,
事件 “混合放在一起的某一零件是合格品”
则 , ,
,
即 ,
解得: ,所以 ,
的可能取值为 ,且由题意知: ,
所以 , ,, ,
所以 的分布列为:
.
(3)证明:因为在甲工厂提高质量指标的条件下,该大型企业把零件交给甲工厂生产的概率,
大于在甲工厂不提高质量指标的条件下该大型企业把零件交给甲工厂生产的概率,
所以: ,
即 ,因为 ,
所以 ,
由 ,
所以 ,
即得: ,
所以 ,
即 ,
由因为 ,
所以 ,
因为 ,所以 ,所以 .