文档内容
2024 届高三第一学期期中质量监测
数学参考答案及评分建议
一、选择题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 B D A A C B A C
二、选择题:本题共4小题,每小题5分,共20分.
题号 9 10 11 12
答案 BC BD ACD BCD
三、填空题:本题共4小题,每小题5分,共20分.
13. 14. (答案不唯一) 15.5 16.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程成演算步骤.
17.【解】(1) ,
当 ,即 时, ,
此时, 的取值集合为 .
(2) .
设 ,因为 ,所以 ,
因为 在区间 上有且仅有1个极值点,
所以 ,
解得 .
18.【解】(1)因为 ,
学科网(北京)股份有限公司由正弦定理得 ,
所以 ,
因为 ,所以 可知 ,
又因为 ,所以 .
(2)因为 是边 的中点,所以 ,
故 ,故 .
由余弦定理得 ,故 ,
因为 ,所以 .
又因为 ,
平方得 ,
所以 ,
故 的长为 .
19.【解】(1)法一:因为 ,
所以 ,
所以 ,
学科网(北京)股份有限公司所以 是常数列,
所以 ,
所以 .
法二:因为
所以 ,①
所以 ,②
②-①,得 ,
所以 ,
所以 是等差数列,
由 得 ,
所以等差数列 的公差 ,
所以 .
(2) .
当 为偶数时,
.
当 为奇数时, .
学科网(北京)股份有限公司所以 (或 )
20.【解】(1)导函数 ,又 ,
所以曲线 在点 处的切线方程为 ,
即 .
(2)当 时, .
令 ,解得 .
列表如下:
1
- 0 +
极小值
所以当 时, 取最小值 ,
所以 .
(3)由(2)可知, ,当且仅当 时,等号成立,
所以 ,
,
所以 .
学科网(北京)股份有限公司当 时,
.
所以对于任意 成立时,整数 的最小值为3.
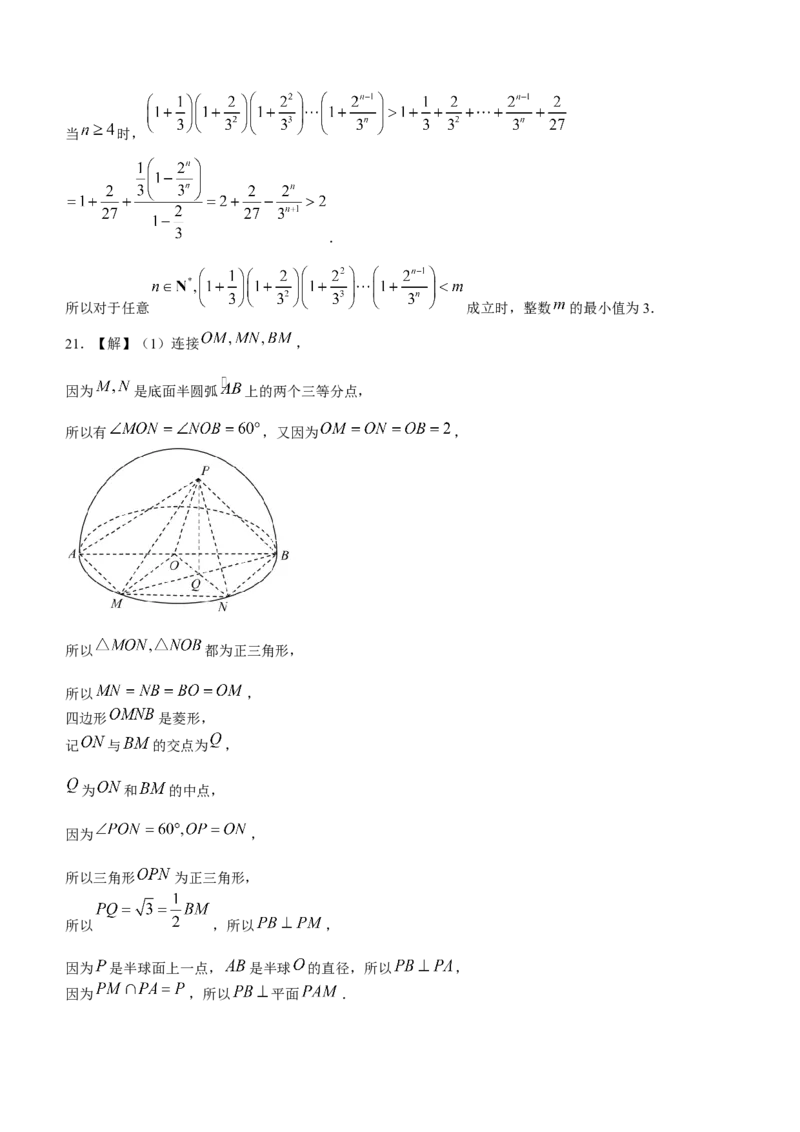
21.【解】(1)连接 ,
因为 是底面半圆弧 上的两个三等分点,
所以有 ,又因为 ,
所以 都为正三角形,
所以 ,
四边形 是菱形,
记 与 的交点为 ,
为 和 的中点,
因为 ,
所以三角形 为正三角形,
所以 ,所以 ,
因为 是半球面上一点, 是半球 的直径,所以 ,
因为 ,所以 平面 .
学科网(北京)股份有限公司(2)因为点 在底面圆内的射影恰在 上,
由(1)知 为 的中点, 为正三角形,所以 ,
所以 底面 ,
因为四边形 是菱形,所以 ,
即 两两互相垂直,
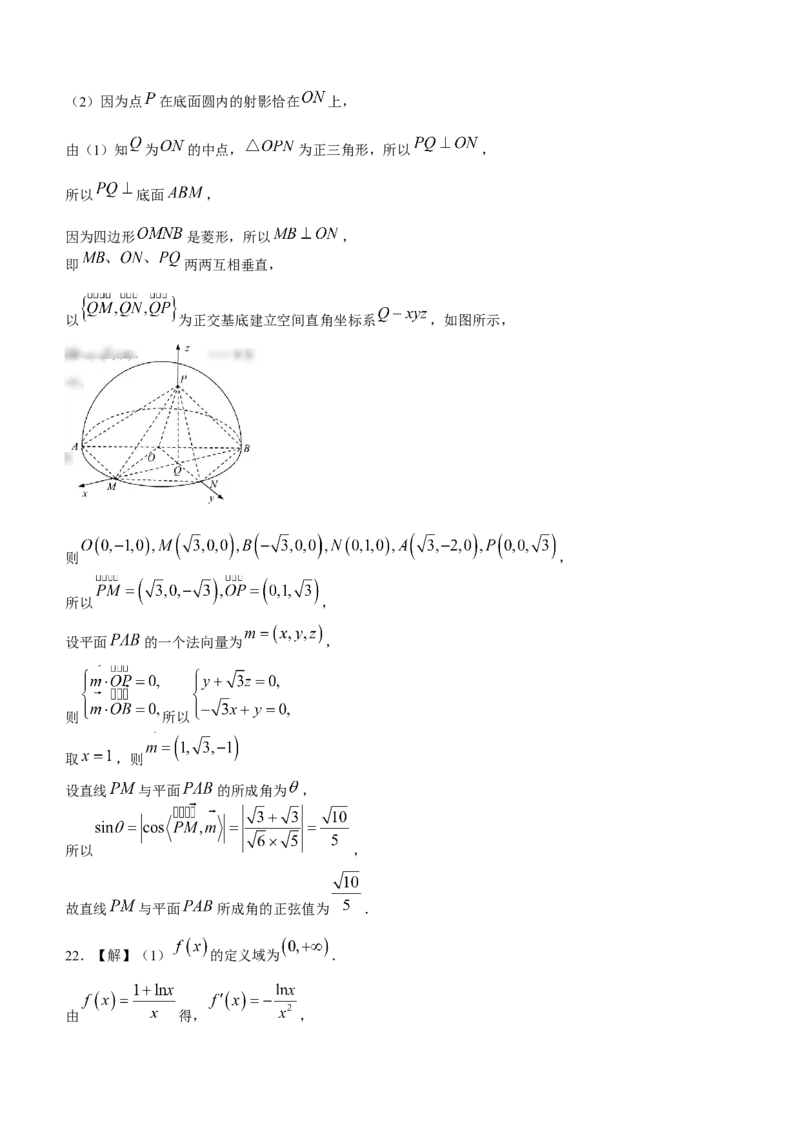
以 为正交基底建立空间直角坐标系 ,如图所示,
则 ,
所以 ,
设平面 的一个法向量为 ,
则 所以
取 ,则
设直线 与平面 的所成角为 ,
所以 ,
故直线 与平面 所成角的正弦值为 .
22.【解】(1) 的定义域为 .
由 得, ,
学科网(北京)股份有限公司当 时, ;当 时, ;当 时, .
故 的递增区间为 ,递减区间为 .
(2)将 变形为 .
令 ,则上式变为 ,
即有 ,
于是命题转换为证明: .
不妨设 ,由(1)知 .
要证 ,
即证 ,
由于 在 上单调递减,故即证 ,
由于 ,故即证 ,
即证 在 上恒成立.
令 ,
则 ,
,
所以 在区间 内单调递增,
所以 ,即 成立.
所以 .
学科网(北京)股份有限公司