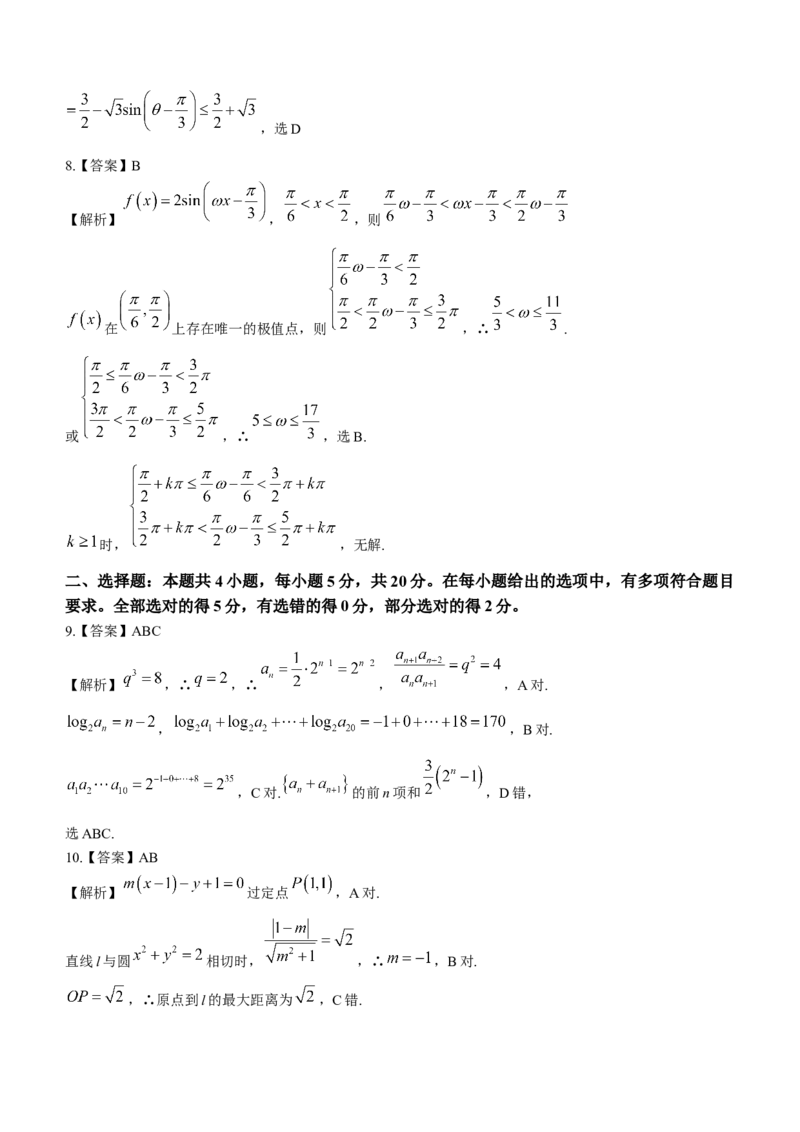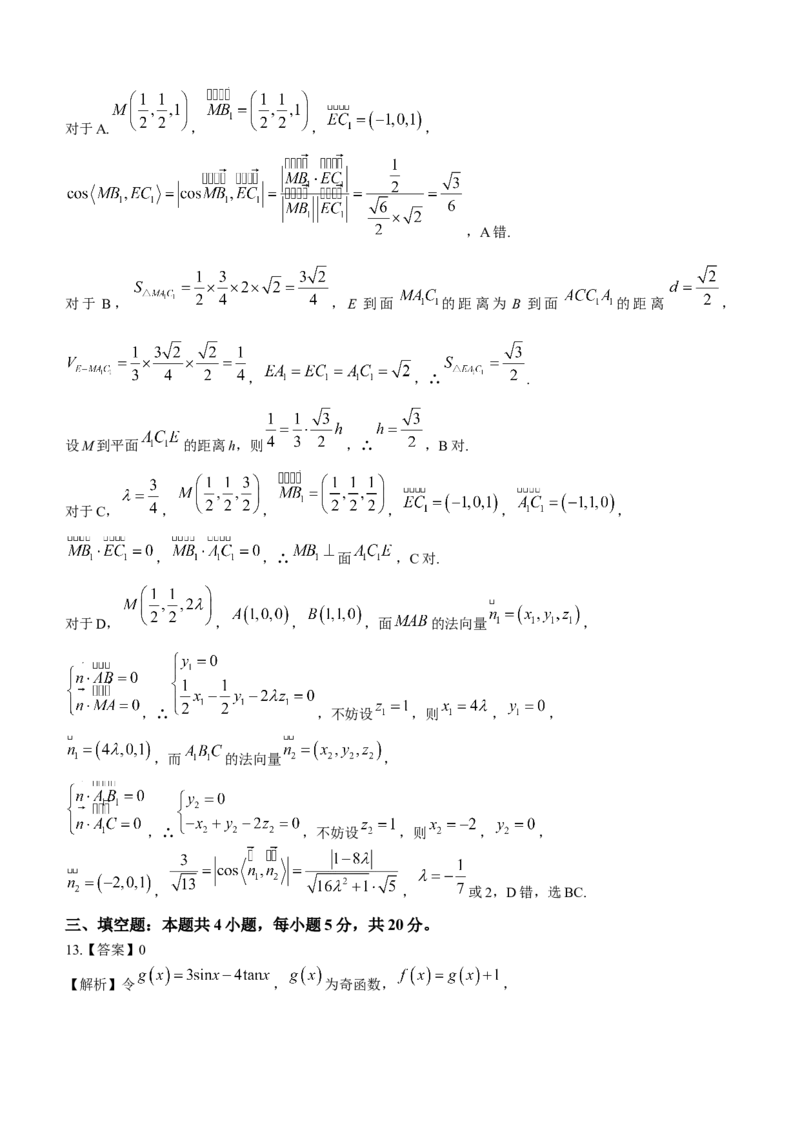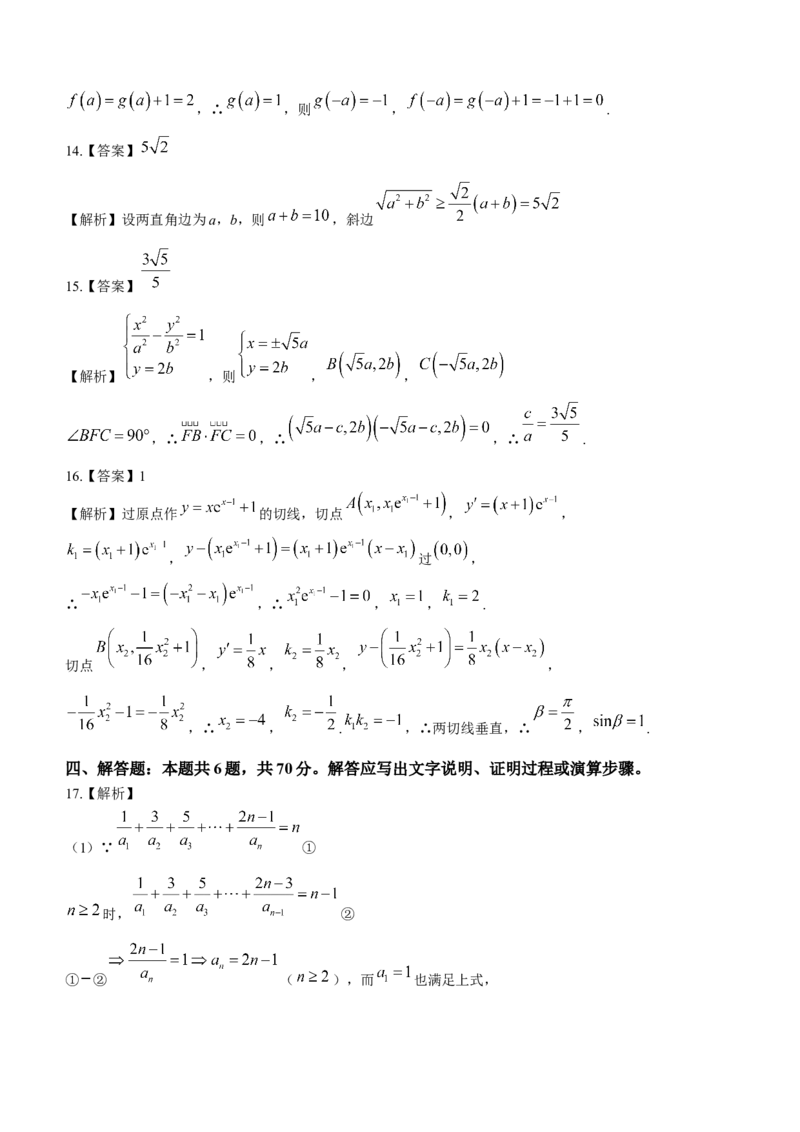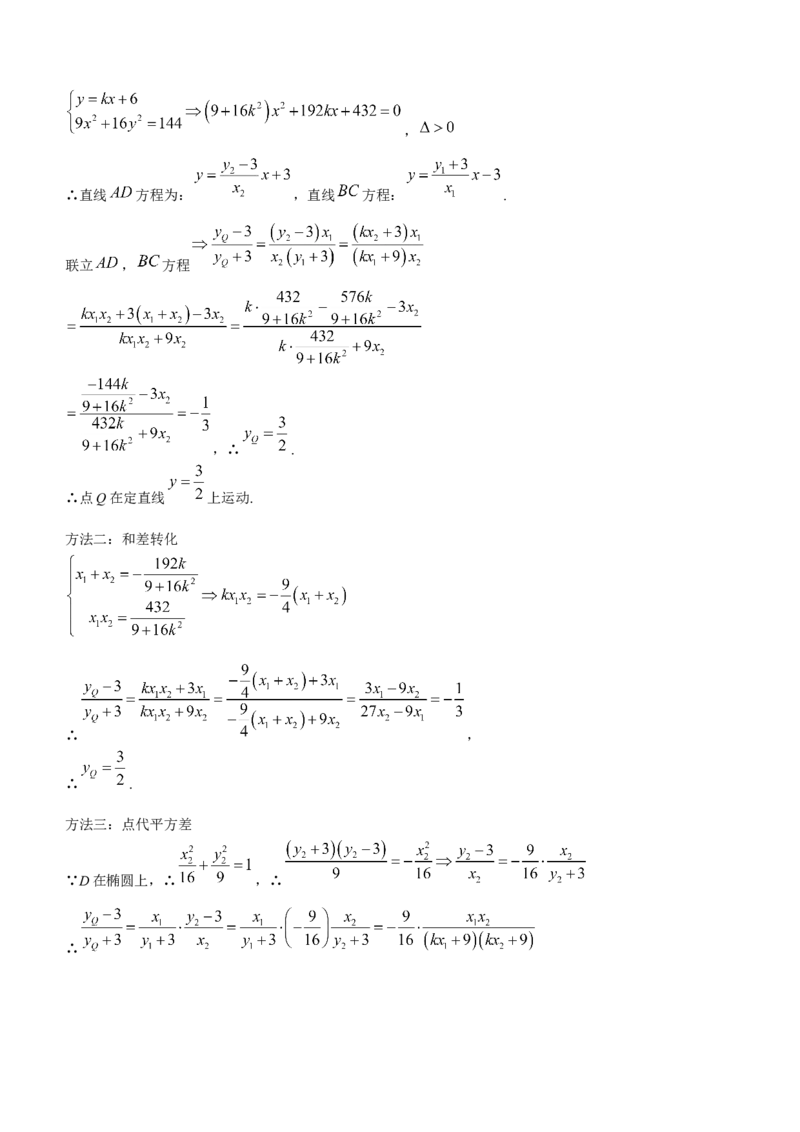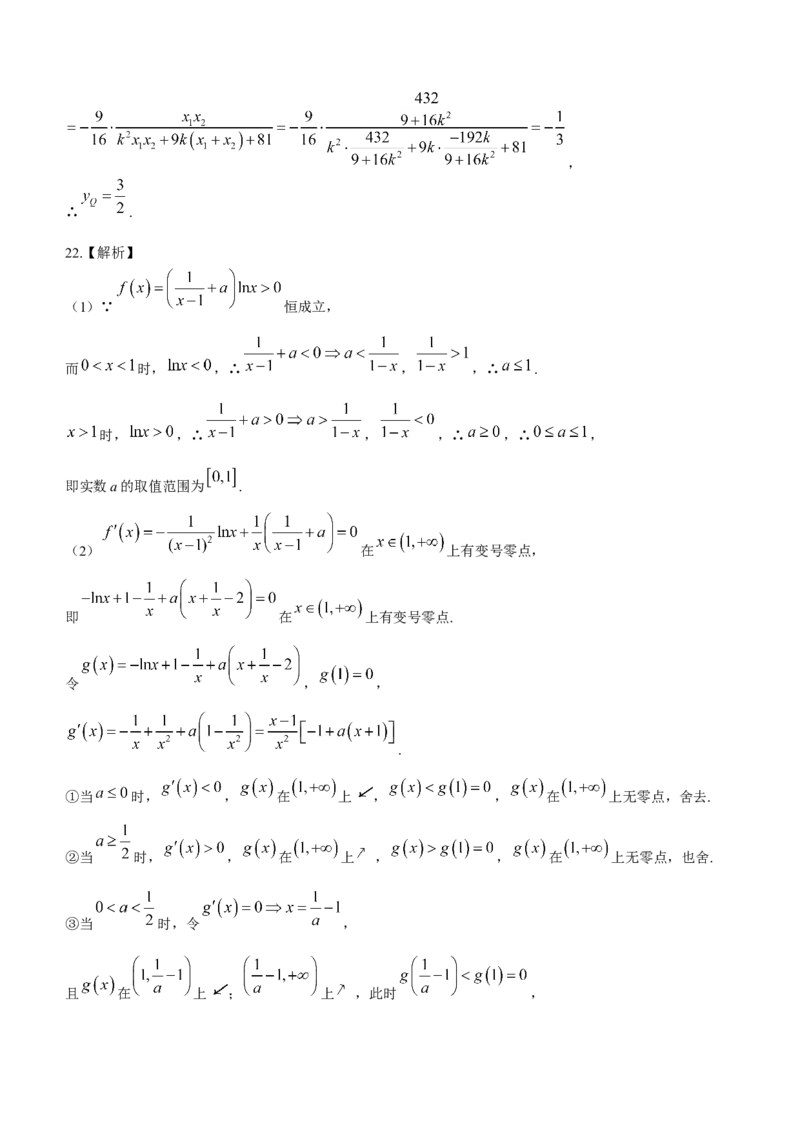文档内容
2022~2023 学年第一学期期中调研考试
高三数学试题
注意事项:
1.考试时间120分钟,试卷满分150分。
2.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
3.请用2B铅笔和0.5毫米黑色墨水签字笔在答题卡上指定区域内作答。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.设m为实数, , .若 ,则 ( )
A.1 B.-1 C.0 D.0或-1
2.“ ”是“ ”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.设 , ( ),若 ,则 ( )
A. B. C. D.
4.连云港海滨浴场是我省最优质的天然海滨浴场,浪缓滩平,水清沙细,当阳光射入海水后,海水中的光照
强度随着深度增加而减弱,可用 表示其总衰减规律,其中K是平均消光系数,D(单位:米)
是海水深度, (单位:坎德拉)和 (单位:坎德拉)分别表示在深度 D处和海面的光强.已知某海区5
米深处的光强是海面光强的40%,则该海区消光系数K的值约为(参考数据: , )(
)
A.0.2 B.0.18 C.0.16 D.0.14
5.已知 ,则 ( )
A.5 B. C.-5 D.
6.若 , , ,则( )A. B. C. D.
7.设 , , 都是单位向量,且 与 的夹角为60°,则 的最大值为( )
A. B. C. D.
8.若函数 在 上存在唯一的极值点,则正数 的取值范围是( )
A. B.
C. D.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目
要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.在等比数列 中, , ,则( )
A. 的公比为4 B. 的前20项和为170
C. 的前10项积为 D. 的前n项和为
10.已知直线l: ( ),则( )
A.直线l过定点 B.直线l与圆 相切时,m的值是-1
C.原点到直线l的最大距离为2 D.直线l与圆 相交
11.定义在 的函数 满足 ,且当 时, ,则(
)
A. 是奇函数 B. 在 上单调递减
C. D.
12.在正四棱柱 中, , .H, ,E分别为 , , 的中点,点M在直线 上, , .下列说法正确的有( )
A.当 时, 与 所成角的余弦值为
B.当 时,点M到平面 的距离为
C.当 时, 平面
D.若平面 与平面 所成锐二面角的余弦值为 ,则
三、填空题:本题共4小题,每小题5分,共20分。
13.已知 ,若 ,则 ____________.
14.若直角三角形两条直角边的和为10,则其斜边的最小值是___________.
15.点 F 为双曲线 ( , )的右焦点,直线 与双曲线交于 B,C 两点,且
,则该双曲线的离心率为___________.
16.如图,对于曲线G所在平面内的点O,若存在以O为顶点的角a,使得对于曲线G上的任意两个不同的点
A,B恒有 成立,则称角 为曲线G的相对于点O的“界角”,并称其中最小的“界角”为曲线
G的相对于点O的“确界角”.已知曲线C: (其中e是自然对数的底数),点O为坐标
原点,曲线C的相对于点O的“确界角”为 ,则 ____________.
四、解答题:本题共6题,共70分。解答应写出文字说明、证明过程或演算步骤。17.(10分)
已知数列 满足 .
(1)求数列 的通项公式
(2)若 ,数列 的前n项和为 ,证明: .
18.(12分)
在 中,角A,B,C所对的边分别为a,b,c.已知 , .
(1)证明: ;
(2)若 的面积为 ,求b.
19.(12分)
如图,在几何体 中,四边形 是边长为3的正方形,平面 与平面 的交线为
.
(1)证明: ;
(2)若平面 平面 ,H为 的中点, , , ,求该几何体的体积.
20.(12分)
某高中有50名学生参加数学竞赛,得分(满分:150分)如下:
女生 1 4 5 5 3 2
男生 0 2 4 12 9 3
(1)若得分不低于120分的学生称为“数学优秀者”.问:是否有95%的把握认为“数学优秀者”与性别有
关;
(2)若在竞赛得分不低于130分的男生中随机抽取3人,求这3人中至少有1人得分在 内的概率.附: ,其中 .
0.05 0.025 0.010 0.001
3.841 5.024 6.635 10.828
21.(12分)
己知椭圆 经过点 .
(1)求椭圆的标准方程;
(2)过点 的直线1交该椭圆于C,D两点(点C在点D的上方),椭圆的上、下顶点分别为A,
B,直线 与直线 交于点Q.证明:点Q在定直线上.
22.(12分)
已知函数 .
(1)若 恒成立,求实数a的取值范围;
(2)若 在区间 上存在极值,求实数a的取值范围.
2022~2023 学年第一学期期中调研考试
高三数学试题
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是
符合题目要求的。
1.【答案】B
【解析】 ,则 或 ,∴ 或0
时, , , ,满足.
时, , , ,不满足,选B.
2.【答案】A
【解析】“ ”,则 ,则一定有 ,充分.
时,不一定有 ,不必要,选A.3.【答案】A
【解析】
,∴ ,∴ ,选A.
4.【答案】B
【解析】 ,∴ ,∴ ,
∴ ,选B.
5.【答案】D
【解析】 ,则
,
, ,
∴ ,选D
6.【答案】C
【解折】 , , ,∴a最小.
, , , ,∴ ,选C.
7.【答案】D
【解析】设 , , , .,选D
8.【答案】B
【解析】 , ,则
在 上存在唯一的极值点,则 ,∴ .
或 ,∴ ,选B.
时, ,无解.
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目
要求。全部选对的得5分,有选错的得0分,部分选对的得2分。
9.【答案】ABC
【解析】 ,∴ ,∴ , ,A对.
, ,B对.
,C对. 的前n项和 ,D错,
选ABC.
10.【答案】AB
【解析】 过定点 ,A对.
直线l与圆 相切时, ,∴ ,B对.
,∴原点到l的最大距离为 ,C错.圆 ,化简 ,圆心 , ,
在圆上,直线l与圆可能相切,D错,选AB.
11.【答案】AC
【解析】 时, ,∴ , ,
, ,∴ 为奇函数,A对.
, 时, ,∴ ,C对.
时, ,而 ,∴ 不可能单调减,B错.
令 ,则 , ,
,∴ ,
则 ,即 ,则 在 ,
,D错,选AC.
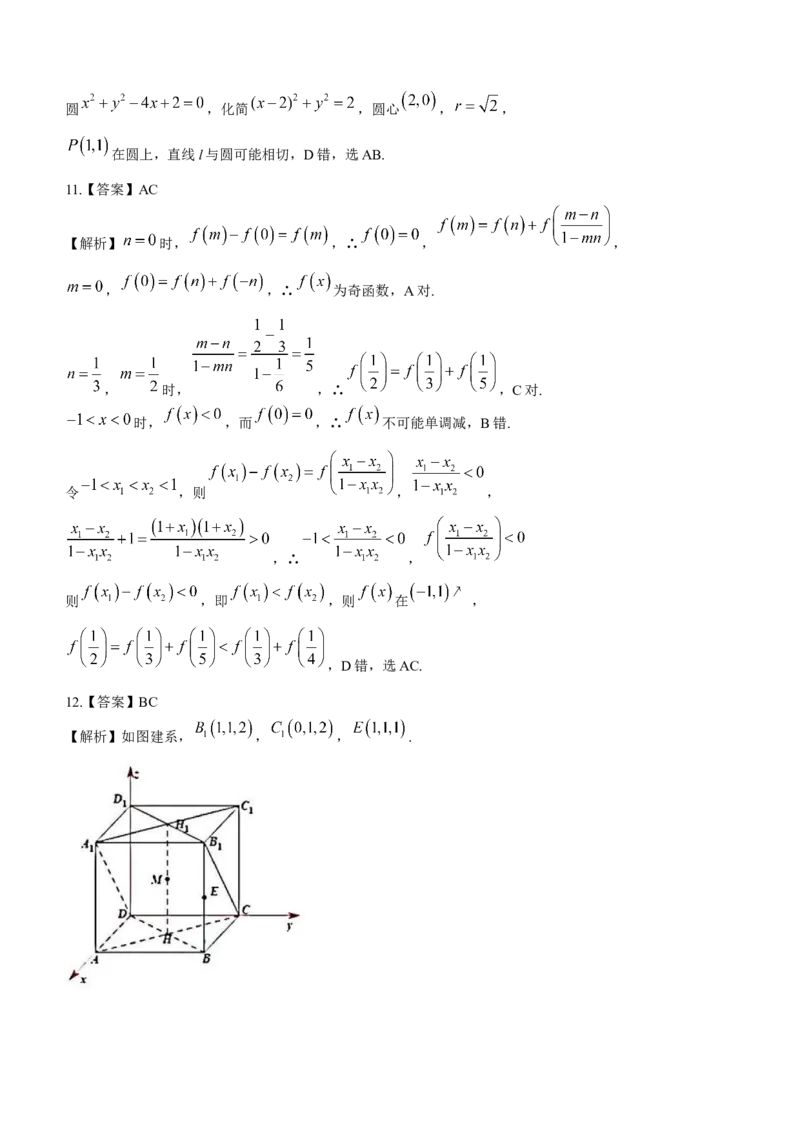
12.【答案】BC
【解析】如图建系, , , .对于A. , , ,
,A错.
对于 B, ,E 到面 的距离为 B 到面 的距离 ,
, ,∴ .
设M到平面 的距离h,则 ,∴ ,B对.
对于C, , , , , ,
, ,∴ 面 ,C对.
对于D, , , ,面 的法向量 ,
,∴ ,不妨设 ,则 , ,
,而 的法向量 ,
,∴ ,不妨设 ,则 , ,
, , 或2,D错,选BC.
三、填空题:本题共4小题,每小题5分,共20分。
13.【答案】0
【解析】令 , 为奇函数, ,,∴ ,则 , .
14.【答案】
【解析】设两直角边为a,b,则 ,斜边
15.【答案】
【解析】 ,则 , ,
,∴ ,∴ ,∴ .
16.【答案】1
【解析】过原点作 的切线,切点 , ,
, 过 ,
∴ ,∴ , , .
切点 , , , ,
,∴ , . ,∴两切线垂直,∴ , .
四、解答题:本题共6题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.【解析】
(1)∵ ①
时, ②
① ② ( ),而 也满足上式,∴ .
(2)
∴ .
18.【解析】
(1)证明:
∴ , .
∴ .
(2) .
∴ .
19.【解析】
(1)证明:∵ ,而 平面 , 平面 ,
∴ 平面 ,又∵ 平面 ,
平面 平面 ,∴ ,∴ .
(2)∵ , ,H为 中点,∴ .
而 ,∴ ,∵平面 平面 .
平面 平面 ,∴ 平面 .过E分别作 交 于点I, 交 于点J,连接 .
∴ .
20.【解析】
(1)2×2列联表如下:
数学是否优秀
数学优秀者 不优秀 合计
性别
男 24 6 30
女 10 10 20
合计 34 16 50
∴有95%的把握认为“数学优秀者”与性别有关.
(2)得分不低于130分的男生有12人,其中得分在 内的有3人.
∴3人中至少有1人得分在 内的概率 .
21.【解析】
(1)∵椭圆过点M,∴ ,
∵ ,∴ ,
∴椭圆的标准方程为 .
(2)方法一:设直线l的方程为 , , , ,,
∴直线 方程为: ,直线 方程: .
联立 , 方程
,∴ .
∴点Q在定直线 上运动.
方法二:和差转化
∴ ,
∴ .
方法三:点代平方差
∵D在椭圆上,∴ ,∴
∴,
∴ .
22.【解析】
(1)∵ 恒成立,
而 时, ,∴ , ,∴ .
时, ,∴ , ,∴ ,∴ ,
即实数a的取值范围为 .
(2) 在 上有变号零点,
即 在 上有变号零点.
令 , ,
.
①当 时, , 在 上 , , 在 上无零点,舍去.
②当 时, , 在 上 , , 在 上无零点,也舍.
③当 时,令 ,
且 在 上 ; 上 ,此时 ,∴ 在 上有唯一的变号零点,符合.
综上:实数a的取值范围为 .