文档内容
完成时间: 月 日 天气:
作业 04 平面向量的概念及其线性运算
1.向量的有关概念
(1)向量:既有大小又有方向的量叫做向量,向量的大小叫做向量的模.
(2)零向量:长度为0的向量,其方向是任意的.
(3)单位向量:长度等于1个单位的向量.
(4)平行向量:方向相同或相反的非零向量,又叫共线向量,规定:0与任一向量平行.
(5)相等向量:长度相等且方向相同的向量.
(6)相反向量:长度相等且方向相反的向量.
2.向量的线性运算
向量运算 定义 法则(或几何意义) 运算律
交换律:a+b=b+a;
加法 求两个向量和的运算 结合律:
(a+b)+c=a+(b+c)
求a与b的相反向量
减法 -b的和的运算 a-b=a+(-b)
|λ a|=|λ||a|,当λ>0时,
λa与a的方向相同;当 λ(μ a)=(λμ)a;(λ+μ)a
求实数λ与向量a的
数乘 λ<0 时,λa 与 a 的方向 =λa+μa;
积的运算
相反;当λ=0时,λa= λ(a+b)=λa+λb
0
4.向量的坐标运算
(1)两点间的向量坐标公式:
, , 终点坐标 始点坐标
(2)向量的加减法
, ,
(3)向量的数乘运算
学科网(北京)股份有限公司,则:
(4)向量的模
,则 的模
(5)相反向量
已知 ,则 ;已知
(6)单位向量
一、单选题
1.下列命题中正确的是( )
A.零向量没有方向 B.共线向量一定是相等向量
C.若向量 , 同向,且 ,则 D.单位向量的模都相等
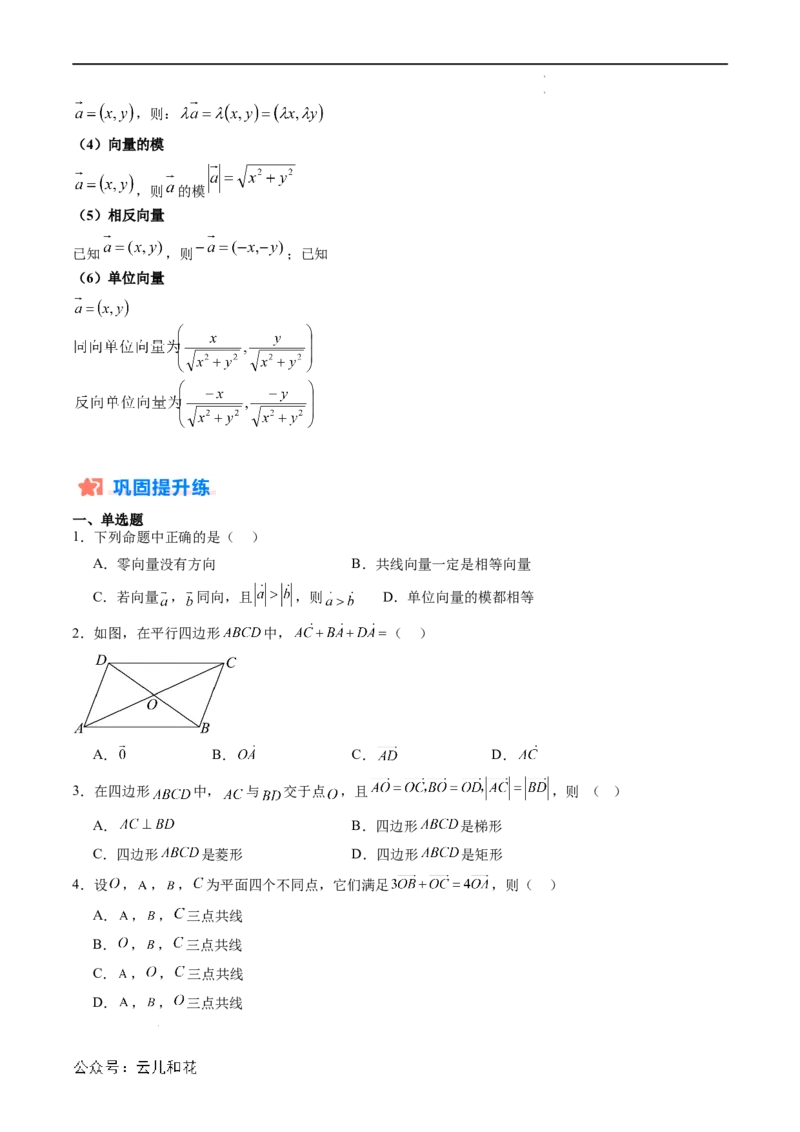
2.如图,在平行四边形 中, ( )
A. B. C. D.
3.在四边形 中, 与 交于点 ,且 ,则 ( )
A. B.四边形 是梯形
C.四边形 是菱形 D.四边形 是矩形
4.设 , , , 为平面四个不同点,它们满足 ,则( )
A. , , 三点共线
B. , , 三点共线
C. , , 三点共线
D. , , 三点共线
学科网(北京)股份有限公司5.设 是非零向量,则 是 成立的( )
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件
二、多选题
6.已知点 , , ,则以 , , 为顶点的平行四边形的第四个顶点 的坐标为
( )
A. B. C. D.
7.向量 , , ,若A,B,C三点共线,则k的值可能为( )
A.2 B.-2 C.11 D.-11
8.已知点 , ,向量 , ∥ ,则( )
A. 时 与 方向相同
B. 时, 与 方向相同
C. 时 与 方向相反
D. 时, 与 方向相反
三、填空题
9.已知向量 ,若 ,则 .
10.已知 , 是不共线的向量,且 , , ,若 、 、 三点共线,
则 .
四、解答题
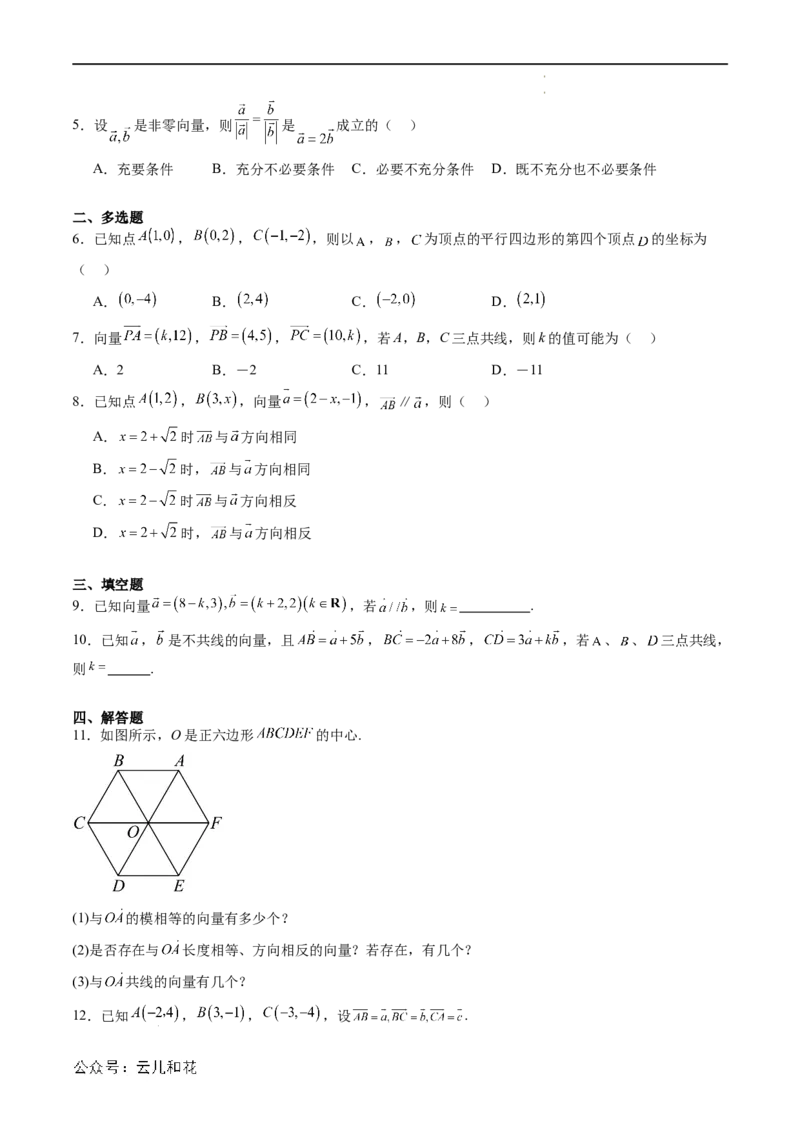
11.如图所示,O是正六边形 的中心.
(1)与 的模相等的向量有多少个?
(2)是否存在与 长度相等、方向相反的向量?若存在,有几个?
(3)与 共线的向量有几个?
12.已知 , , ,设 .
学科网(北京)股份有限公司(1)求满足 的实数 , 的值;
(2)若线段 靠近点 的三等分点为 ,求 点的坐标.
1.已知向量 不共线, , , ,则
( )
A.A,B,D三点共线 B.A,B,C三点共线
C.B,C,D三点共线 D.A,C,D三点共线
2.已知 为非零向量,则下列说法错误的是( )
A.若 ,则 与 方向相同
B.若 ,则 与 方向相反
C.若 ,则 与 有相等的模
D.若 ,则 与 方向相同
3.已知向量 , , , ,若 ,则 的最小值为 .
4.已知点 ,向量 , ,点 是线段 的三等分点,则点 的坐标是( )
A. B. C. 或 D. 或
5.已知点O是平面上一定点,A,B,C是平面上不共线的三个点,动点P满足
,则点P的轨迹一定通过 的( )
A.外心 B.内心 C.重心 D.垂心
1.如图所示, 为线段 外一点,若 中任意相邻两点间的距离相等,
,则 ( )
A. B.
学科网(北京)股份有限公司C. D.
2.若 为 的垂心, ,则 = , .
3.设向量 ,其中 .若 ,则 的最小值为 .
1.(上海·高考真题)在平行四边形ABCD中,下列结论中错误的是( )
A. B. C. D.
2.(安徽·高考真题)已知向量 ,且 ,则 的值分别为( )
A.-2,1 B.1,-2 C.2,-1 D.-1,2
3.(广东·高考真题)已知平面向量 , ,且 ,则 等于( )
A.(-2,-4) B.(-3,-6) C.(-5,-10) D.(-4,-8)
4.(全国·高考真题)设向量 , 不平行,向量 与 平行,则实数 .
5.(山东·高考真题)已知向量 与 且 则一定共线的三点是
( )
A.A,C,D三点 B.A,B,C三点
C.A,B,D三点 D.B,C,D三点
学科网(北京)股份有限公司