文档内容
大联考雅礼中学 2024 届高三月考试卷(三)
数 学
命题人:黄启光 审题人:李群丽
得分:
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 8页.时量120分钟,满分150
分.
第Ⅰ卷
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知复数 ( 为虚数单位), 是z的共轭复数,则 的值为
A.1 B. C. D.
2.设全集 , , ,则
A. B. C. D.
3.已知向量 , 满足 , , ,则
A.5 B.3 C.2 D.1
4.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先成果,哥德巴赫猜想如下:每个大于 2的偶数
都可以表示为两个素数(一个整数除了 1和它本身没有其他约数的数称为素数)的和,如 ,
,在不超过25的素数中,随机选取2个不同的数,则这2个数恰好含有这组数的中位数的概率是
A. B. C. D.
5.若函数 在区间 上有极值点,则实数a的取值范围是A. B. C. D.
6.已知 , , .则a,b,c的大小关系是
A. B. C. D.
7.已知 , ,则
A. B. C.6 D.4
8 . 已 知 函 数 的 零 点 分 别 为 , , … , , ) , 则
A. B. C.0 D.2
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目
要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.已知随机变量X服从正态分布 ,则下列选项正确的是(参考数值:随机变量 服从正态分布
,则 , ,
)
A. B.
C. D.
10.下列说法正确的是
A.若不等式 的解集为 ,则
B.若命题p: , ,则p的否定为: ,
C.在△ABC中,“ ”是“ ”的充要条件D.若 对 恒成立,则实数x的取值范围为
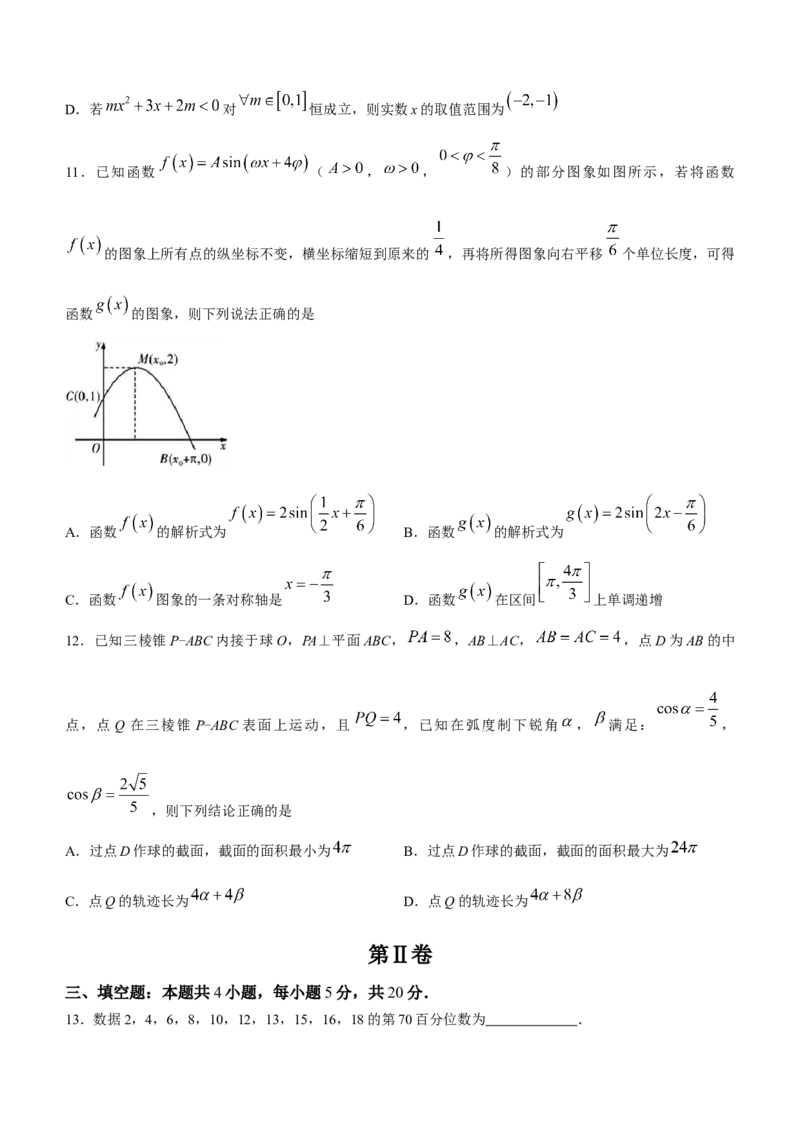
11.已知函数 ( , , )的部分图象如图所示,若将函数
的图象上所有点的纵坐标不变,横坐标缩短到原来的 ,再将所得图象向右平移 个单位长度,可得
函数 的图象,则下列说法正确的是
A.函数 的解析式为 B.函数 的解析式为
C.函数 图象的一条对称轴是 D.函数 在区间 上单调递增
12.已知三棱锥P-ABC内接于球O,PA⊥平面ABC, ,AB⊥AC, ,点D为AB的中
点,点 Q 在三棱锥 P-ABC 表面上运动,且 ,已知在弧度制下锐角 , 满足: ,
,则下列结论正确的是
A.过点D作球的截面,截面的面积最小为 B.过点D作球的截面,截面的面积最大为
C.点Q的轨迹长为 D.点Q的轨迹长为
第Ⅱ卷
三、填空题:本题共4小题,每小题5分,共20分.
13.数据2,4,6,8,10,12,13,15,16,18的第70百分位数为 .14.已知F是双曲线 的左焦点, ,P是双曲线右支上的一动点,则 的最小值
为 .
15.若 的展开式中第4项是常数项,则 除以9的余数为 .
16.已知函数 的定义域为 ,且 ,函数 在
区间 内的所有零点为 ( ,2,3,…,n).若 ,则实数 a 的取值范围是
.
四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、
证明过程或演算步骤.
17.(本小题满分10分)
半径为R的圆内接△ABC, ,∠ACB为锐角.
(1)求∠ACB的大小;
(2若∠ACB的平分线交AB于点D, , ,求△ABC的面积.
18.(本小题满分12分)
已知数列 是首项为正数的等差数列,数列 的前n项和为 .
(1)求数列 的通项公式;
(2)设 ,求数列 的前n项和 .
19.(本小题满分12分)
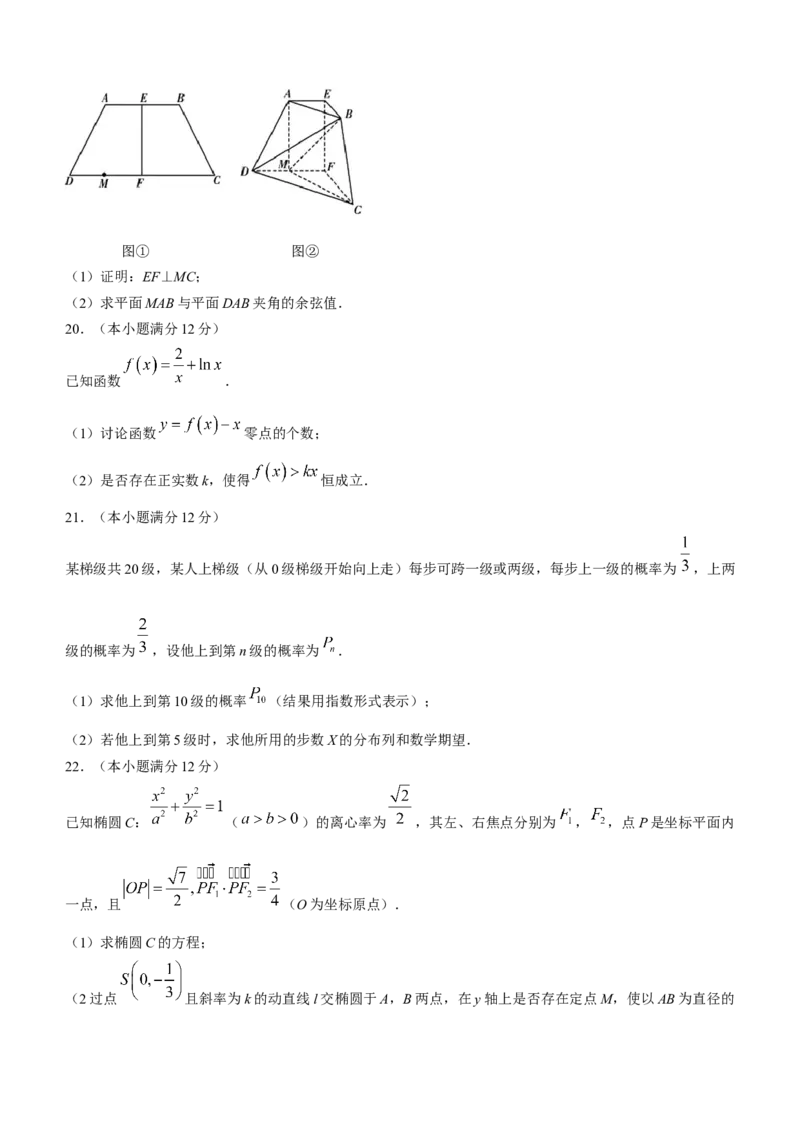
如图①,在等腰梯形ABCD中,AB∥CD,E,F分别为AB,CD的中点, ,M为DF
的中点.现将四边形BEFC沿EF折起,使平面BEFC⊥平面AEFD,得到如图②所示的多面体.在图②中,图① 图②
(1)证明:EF⊥MC;
(2)求平面MAB与平面DAB夹角的余弦值.
20.(本小题满分12分)
已知函数 .
(1)讨论函数 零点的个数;
(2)是否存在正实数k,使得 恒成立.
21.(本小题满分12分)
某梯级共20级,某人上梯级(从0级梯级开始向上走)每步可跨一级或两级,每步上一级的概率为 ,上两
级的概率为 ,设他上到第n级的概率为 .
(1)求他上到第10级的概率 (结果用指数形式表示);
(2)若他上到第5级时,求他所用的步数X的分布列和数学期望.
22.(本小题满分12分)
已知椭圆C: ( )的离心率为 ,其左、右焦点分别为 , ,点P是坐标平面内
一点,且 (O为坐标原点).
(1)求椭圆C的方程;
(2过点 且斜率为k的动直线l交椭圆于A,B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过点M?若存在,求出点M的坐标和△MAB面积的最大值;若不存在,说明理由.
大联考雅礼中学 2024 届高三月考试卷(三)
数学参考答案
一、二、选择题
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B D D C C B A A AC AD ABD ABD
2.D
【解析】易知 , ,∴ ,故 .
故选D.
3.D
【解析】由条件 知 , 同向共线,所以 ,故选D.
4.C
【解析】不超过25的素数有2,3,5,7,11,13,17,19,23共9个,中位数为11,任取两个数含有1l的
概率为 ,故选C.
5.C
【解析】由题意 在区间 上有零点,∴ , ,
∴ ,又当 时, , 单调,不符合,∴ ,∴ ,故
选C.
6.B
【解析】∵ ,∴ ,又
,∴ ,∴ .故选B.
7.A
【解析】由条件知 , ,两边同除以得: ,∴ ,从而 ,故选A.
8.A
【解析】由 , 为其中一个零点,
令 ,∵ ,∴令 ,
∵
∴ ,∴ ,∴ ,∴ ,所以 )共有三个零点 ,0,
,∴ ,故选A.
9.AC
【解析】∵随机变量X服从正态分布 ,
正态曲线关于直线 对称,且 , ,从而A正确,B错误,
根据题意可得, , ,
∴ ,故C正确;
与 不关于直线 对称,故D错误.故选AC.
10.AD
【解析】对于A,不等式 解集为 ,则方程 的两根为 ,
2,故 ,则 , ,所以 ,故A正确;对于B,全称命题的否定是特称命题,量词 任 意 改 成 存 在 , 结 论 进 行 否 定 应 是 小 于 等 于 , 故 B 不 正 确 ; 对 于 C ,
,又 ,
所以 或 ,显然不是充要条件,故 C 错误;对于 D,令 ,则
,对 恒成立,则
,解得 ,故D正确,故选AD.
11.ABD
【解析】由图知, , ,∴ ,得 .故 .
∵点 在函数图象上,∴ ,即 .又∵ ,∴ ,∴ .
故函数 的解析式为 ,故A正确;
将 的图象上所有点的纵坐标不变,横坐标缩短到原来的 ,可得 的图象,再将所得
图象向右平移 个单位长度,可得 的图象,故B正确;
当 时, ,不是最值,故直线 不是 图象的一条对称轴,故C不正
确;
当 时, ,则 在 还上单调递增,故D
正确,故选ABD.
12.ABD
【 解 析 】 三 棱 锥 P-ABC 的 外 接 球 即 为 以 AB , AC , AP 为 邻 边 的 长 方 体 的 外 接 球 , ∴
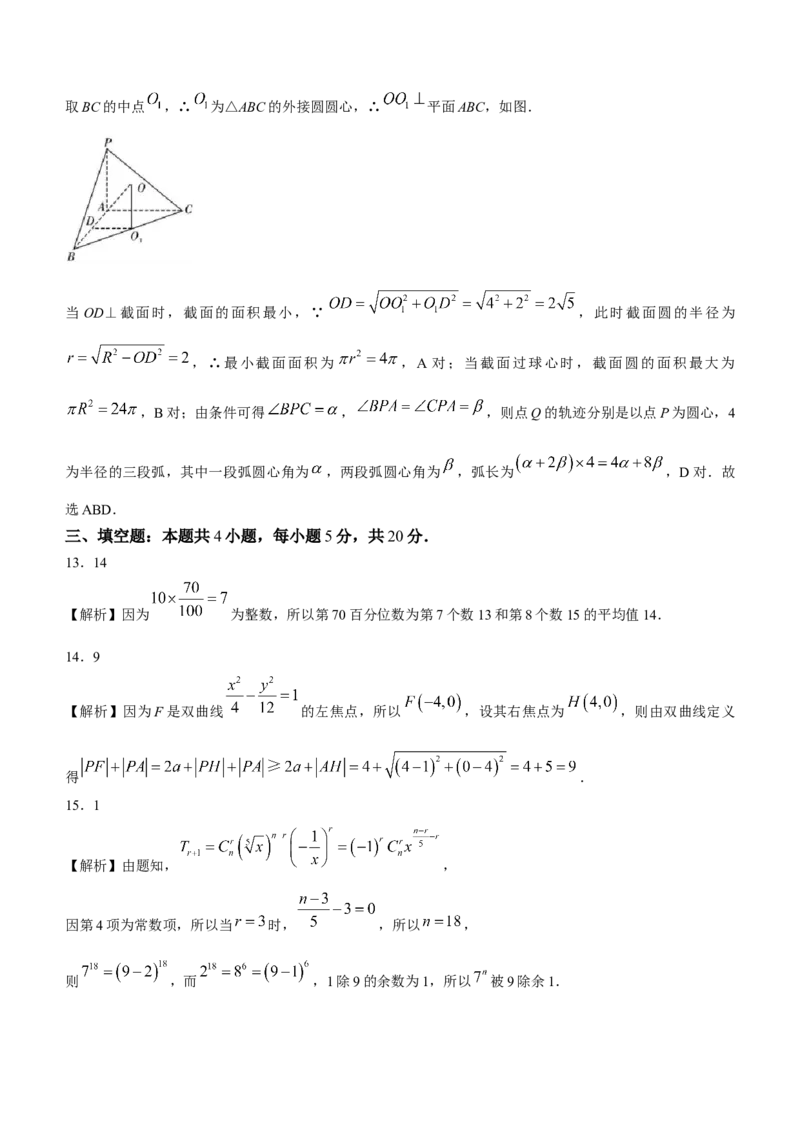
,∴ ,取BC的中点 ,∴ 为△ABC的外接圆圆心,∴ 平面ABC,如图.
当 OD⊥截面时,截面的面积最小,∵ ,此时截面圆的半径为
,∴最小截面面积为 ,A 对;当截面过球心时,截面圆的面积最大为
,B对;由条件可得 , ,则点Q的轨迹分别是以点P为圆心,4
为半径的三段弧,其中一段弧圆心角为 ,两段弧圆心角为 ,弧长为 ,D对.故
选ABD.
三、填空题:本题共4小题,每小题5分,共20分.
13.14
【解析】因为 为整数,所以第70百分位数为第7个数13和第8个数15的平均值14.
14.9
【解析】因为F是双曲线 的左焦点,所以 ,设其右焦点为 ,则由双曲线定义
得 .
15.1
【解析】由题知, ,
因第4项为常数项,所以当 时, ,所以 ,
则 ,而 ,1除9的余数为1,所以 被9除余1.16.
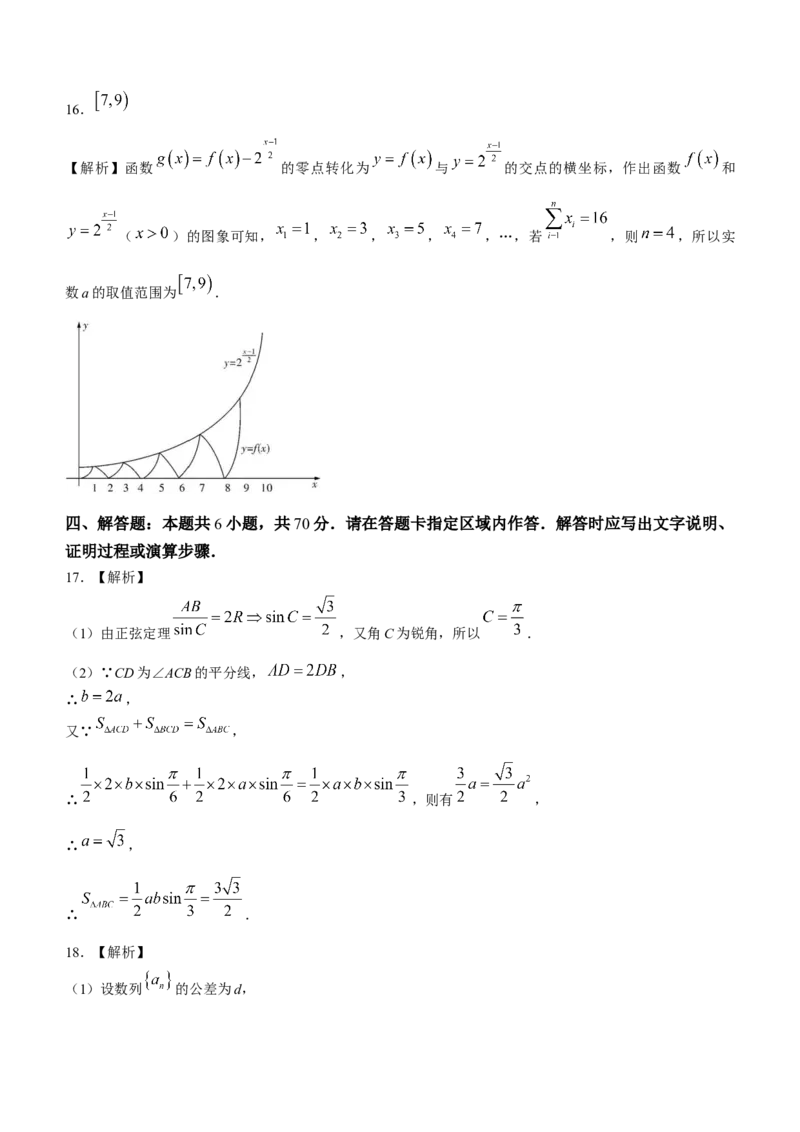
【解析】函数 的零点转化为 与 的交点的横坐标,作出函数 和
( )的图象可知, , , , ,…,若 ,则 ,所以实
数a的取值范围为 .
四、解答题:本题共6小题,共70分.请在答题卡指定区域内作答.解答时应写出文字说明、
证明过程或演算步骤.
17.【解析】
(1)由正弦定理 ,又角C为锐角,所以 .
(2)∵CD为∠ACB的平分线, ,
∴ ,
又∵ ,
∴ ,则有 ,
∴ ,
∴ .
18.【解析】
(1)设数列 的公差为d,令 ,得 ,所以 .①
令 ,得 ,所以 .②
解①②得 , ,所以 .
(2)由(1)知 ,
所以 ,
所以 ,
两式相减,得
.
所以 .
19.【解析】
(1)证明:由题意,可知在等腰梯形ABCD中,AB∥CD,
∵E,F分别为AB,CD的中点,
∴EF⊥CD.
∴折叠后,EF⊥DF,EF⊥CF.
∵ ,DF, 平面DCF,
∴EF⊥平面DCF.
又 平面DCF,
∴EF⊥MC.
(2)∵平面BEFC⊥平面AEFD,平面 平面 ,且平面DF⊥EF, 平面AEFD,
∴DF⊥平面BEFC,又 平面BEFC,
∴DF⊥CF,
∴DF,CF,EF两两垂直.
以F为坐标原点,分别以FD,FC,EF所在直线为.x轴,y轴,z轴建立如图所示的空间直角坐标系F-xyz.
由题意知 .
∴ , , , .
∴ , , .
设平面MAB,平面ABD的法向量分别为 , ,
由 得 ,
取 ,则 为平面MAB的一个法向量.
由 得 ,
取 ,则 为平面ABD的一个法向量.
∴ ,
平面MAB与平面DAB夹角的余弦值 .
20.【解析】
(1)设 ,则 ,
可知 在 上单调递减,又 , ,
所以方程 有且仅有一个根,即函数 有且只有1个零点.(2)令 得 ( ),即 ( ).
设 , ,则 ,
设 , ,则 ,
因为 ,
当 时, ,
当 时, ,
所以函数 在 上单调递增,在 上单调递减,
所以 ,
则 恒成立,
所以函数 在 上单调递减,又 , ,
所以不可能存在正实数k,使得 恒成立.
21.【解析】
(1)由条件知 , ,
且 ( ).
所以 ,
所以 ,又 ,∴ ,∴ .
∴ .
(2)由(1)知此人上到第5级的概率为 ,
X的可能取值为3,4,5
, ,
所以X的分布列为
X 3 4 5
P
所以 .
22.【解析】
(1)设 , , ,则由 ;得 ,
由 得 ,即 .所以 .
又因为 ,所以 , .因此所求椭圆C的方程为 .
(2)设动直线l的方程为: ,由 得 .
设 , .
则 , .假设在y上存在定点 ,满足题设,
则 , .