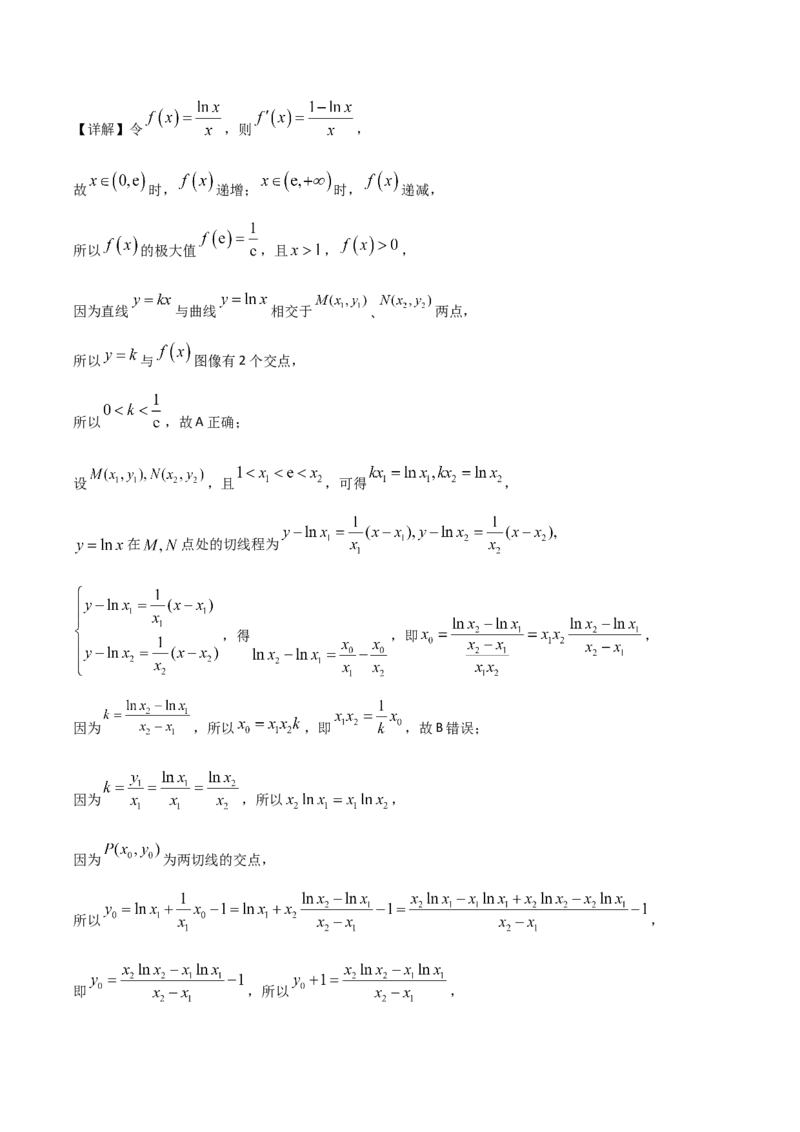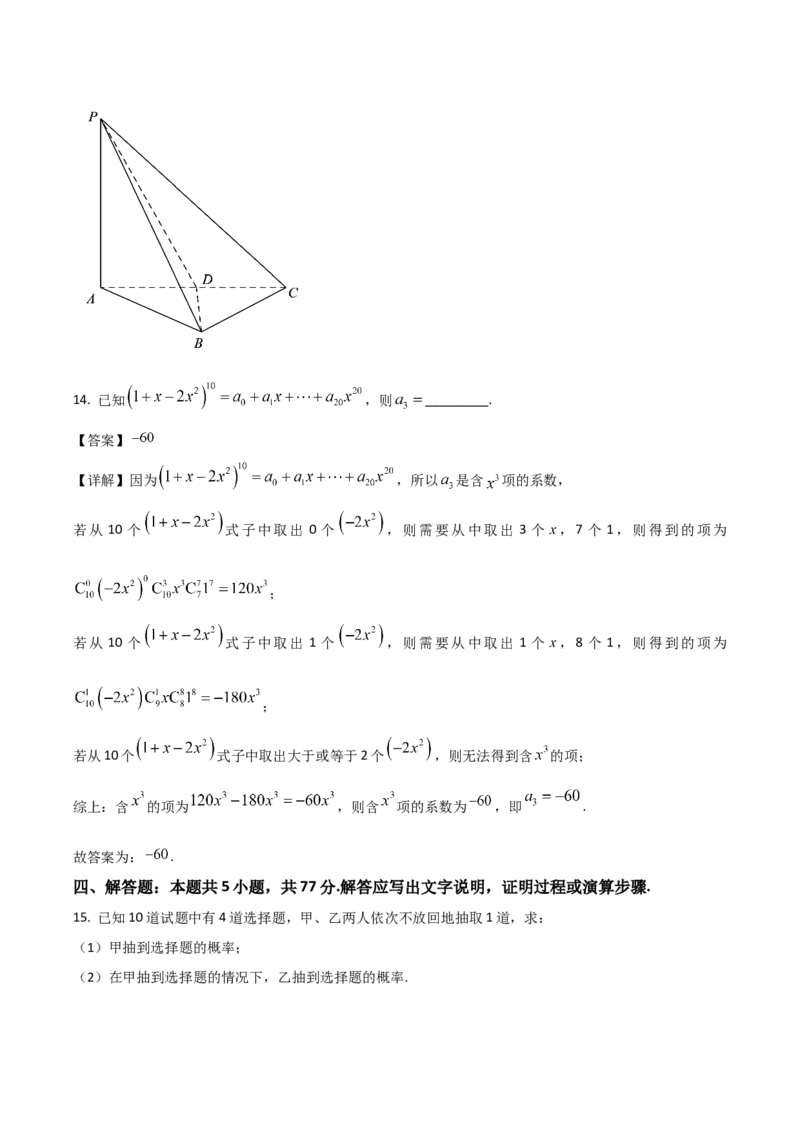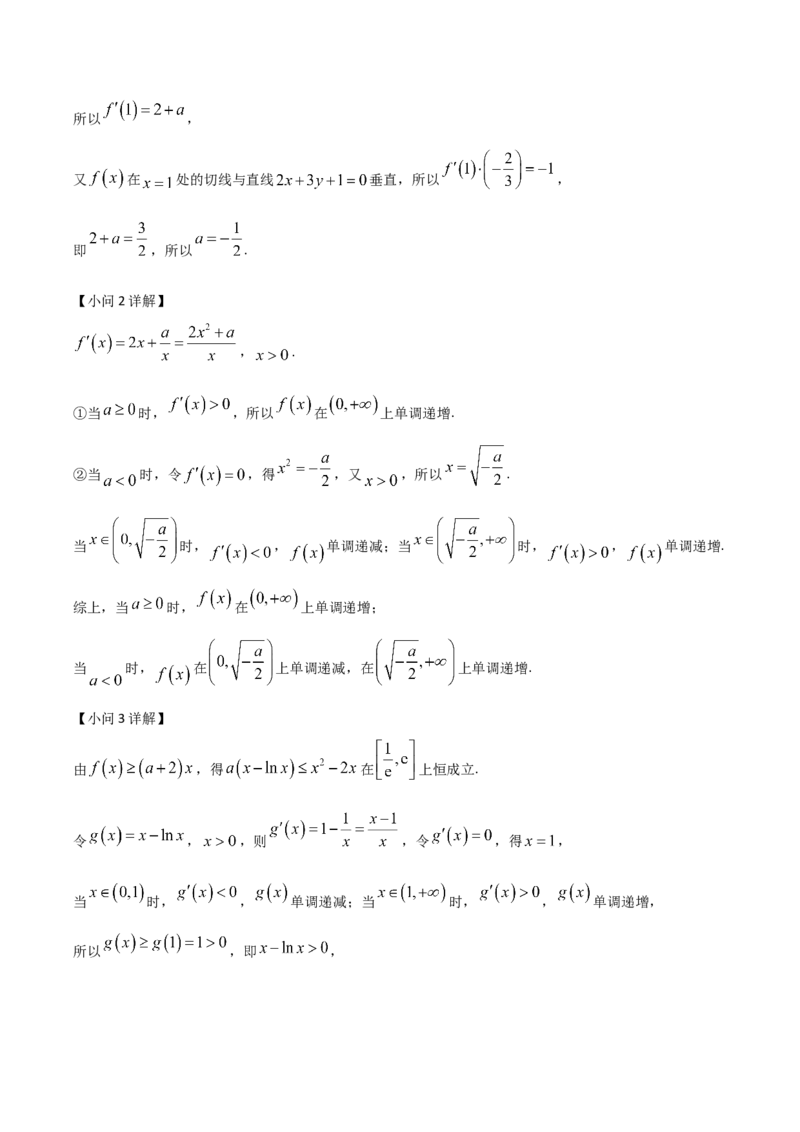文档内容
南京市 2024-2025 学年度第二学期五校联盟期中学情调研
高二数学
本卷:150分 考试时间:120分钟
注意事项:
1.本试卷共4页.本试卷满分为150分,考试时间为120分钟.
2.答卷前,考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置.
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1. 已知平面 的法向量为 ,平面 的法向量为 ,若 ,则k=( )
A. 4 B.
C. 5 D.
【答案】D
【详解】∵ ,∴ ,
∴ ,解得 .
故选:D
2. 已知 ,则 为( )
A. B. 1 C. 32 D. 243
【答案】B
【详解】因为 ,
令 可得 .
故选:B
3. 已知函数 ,则 ( )A. B. C. D.
【答案】D
【详解】设 ,则 ,
∴ ,即 ,
∴ .
故选:D.
4. 某晚会有三个唱歌节目,两个舞蹈节目,要求舞蹈节目不能相邻,有( )种排法?
A. 72 B. 36 C. 24 D. 12
【答案】A
【详解】先排三个唱歌节目这有: 种情况,
然后四个空排两个舞蹈节目这有: 种情况,
所以舞蹈节目不能相邻的情况有: 情况.
故选:A.
5. 被5除的余数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【详解】由题可知, ,
则其展开式的通项公式为 ,
由通项公式可得,只有 时, 不能被5整除,
其余项均能被5整除.故 被5除的余数为1,则 被5除的余数为3.
故选:C.6. 已知 ,直线 过原点且平行于 ,则 到 的距离为( ).
A. B. 1 C. D.
【答案】C
【详解】由题意取 ,则 ,
所以 到 的距离为
.
故选:C
7. 若函数 有两个不同的极值点,则实数 的取值范围为( )
A. B. C. D.
【答案】B
【详解】函数 的定义域为 ,
又 ,
因为函数 有两个不同的极值点,
所以 有两个不同正根,
即 有两个不同正根(不妨设为 ),所以 ,解得 ,即实数 的取值范围为 .
故选:B.
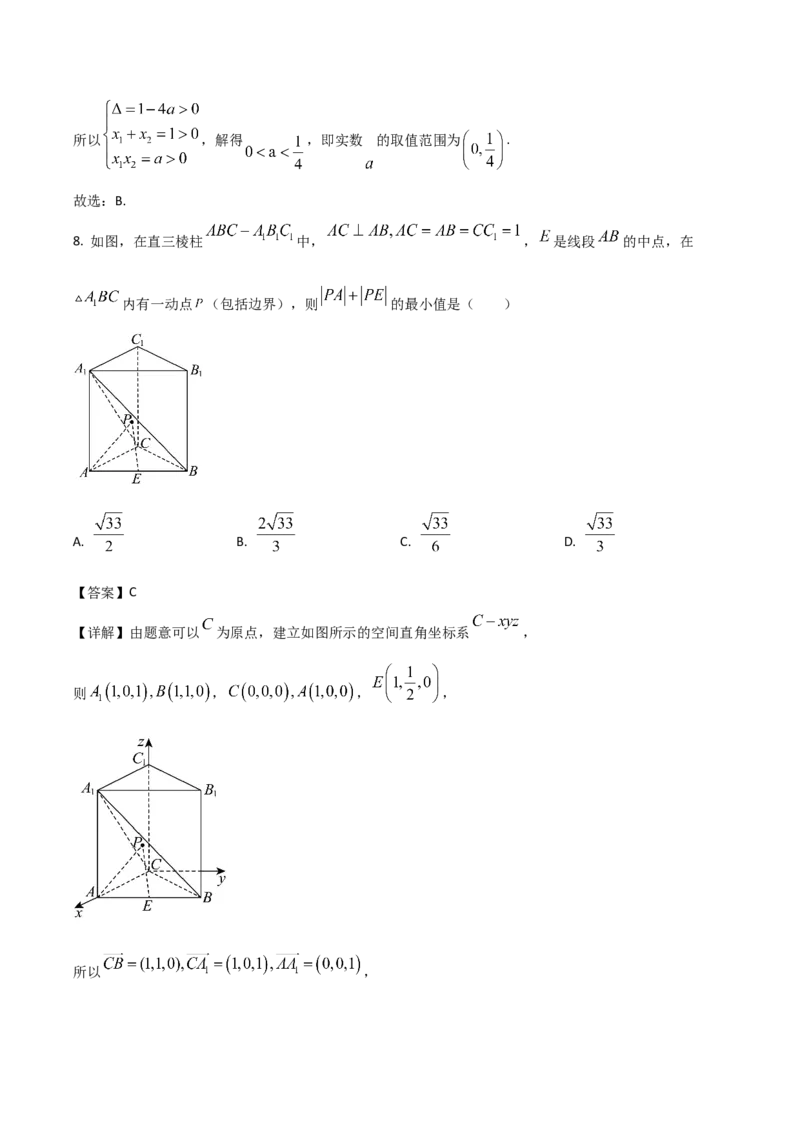
8. 如图,在直三棱柱 中, , 是线段 的中点,在
内有一动点 (包括边界),则 的最小值是( )
A. B. C. D.
【答案】C
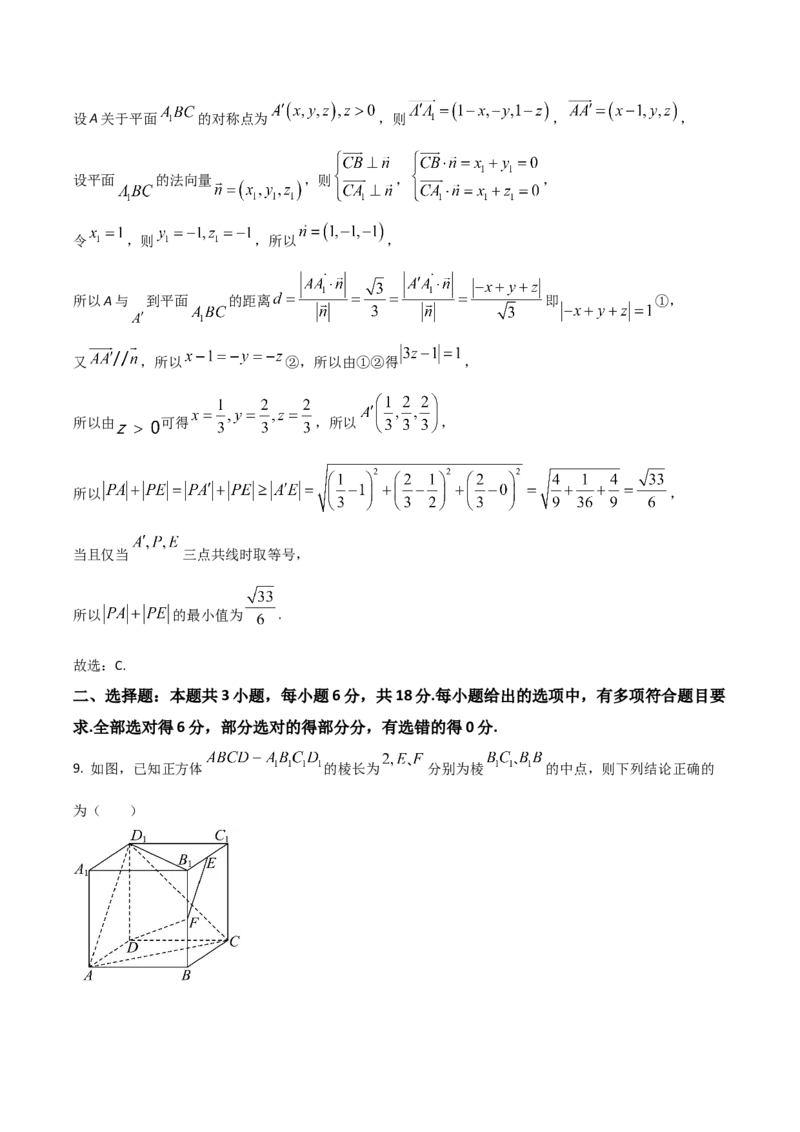
【详解】由题意可以 为原点,建立如图所示的空间直角坐标系 ,
则 , , ,
所以 ,设A关于平面 的对称点为 ,则 , ,
设平面 的法向量 ,则 , ,
令 ,则 ,所以 ,
所以A与 到平面 的距离 即 ①,
又 ,所以 ②,所以由①②得 ,
所以由 可得 ,所以 ,
所以 ,
当且仅当 三点共线时取等号,
所以 的最小值为 .
故选:C.
二、选择题:本题共3小题,每小题6分,共18分.每小题给出的选项中,有多项符合题目要
求.全部选对得6分,部分选对的得部分分,有选错的得0分.
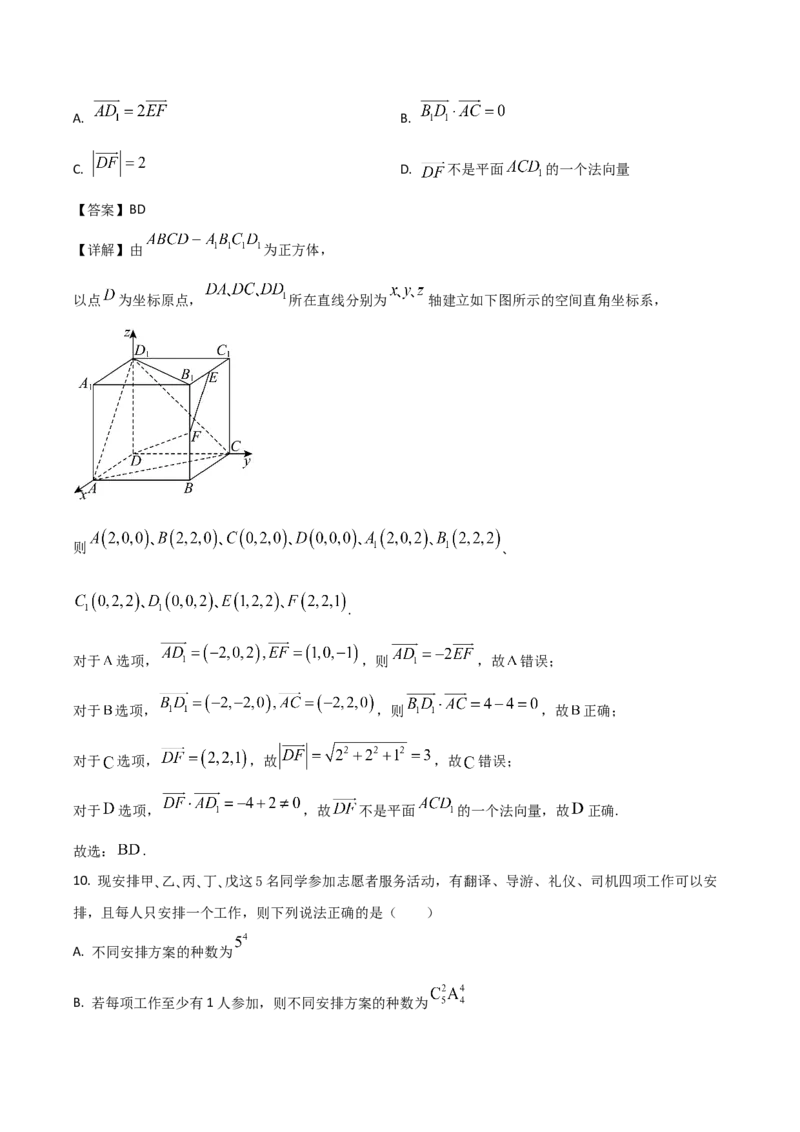
9. 如图,已知正方体 的棱长为 分别为棱 的中点,则下列结论正确的
为( )A. B.
C. D. 不是平面 的一个法向量
【答案】BD
【详解】由 为正方体,
以点 为坐标原点, 所在直线分别为 轴建立如下图所示的空间直角坐标系,
则 、
.
对于 选项, ,则 ,故 错误;
对于 选项, ,则 ,故 正确;
对于 选项, ,故 ,故 错误;
对于 选项, ,故 不是平面 的一个法向量,故 正确.
故选: .
10. 现安排甲、乙、丙、丁、戊这5名同学参加志愿者服务活动,有翻译、导游、礼仪、司机四项工作可以安
排,且每人只安排一个工作,则下列说法正确的是( )
A. 不同安排方案的种数为
B. 若每项工作至少有1人参加,则不同安排方案的种数为C. 若司机工作不安排,其余三项工作至少有1人参加,则不同安排方案的种数为
的
D. 若每项工作至少有1人参加,甲不能从事司机工作,则不同安排方案 种数为
【答案】BD
【详解】对A,若每人都安排一项工作,每人有4种安排方法,则不同安排方案的种数为 ,故A错误;
对B,先将5人分为4组,再将分好的4组全排列,安排4项工作,
则不同安排方案的种数为 ,故B正确;
对C,先将5人分为3组,有 种分组方法,
将分好的三组安排翻译、导游、礼仪三项工作,有 种情况,
则不同安排方案的种数是 ,故C错误;
对D,第一类,先从乙,丙,丁,戊中选出1人从事司机工作,再将剩下的4人分成三组,
安排翻译、导游、礼仪三项工作,则不同安排方案的种数为 ;
第二类,先从乙,丙,丁,戊中选出2人从事司机工作,
再将剩下的3人安排翻译、导游、礼仪三项工作,
则不同安排方案的种数为 .所以不同安排方案的种数是 ,故D正确.
故选:BD
11. 已知直线 与曲线 相交于不同两点 , ,曲线 在点 处的切线
与在点 处的切线相交于点 ,则( )
A. B. C. D.
【答案】ACD【详解】令 ,则 ,
故 时, 递增; 时, 递减,
所以 的极大值 ,且 , ,
因为直线 与曲线 相交于 、 两点,
所以 与 图像有2个交点,
所以 ,故A正确;
设 ,且 ,可得 ,
在 点处的切线程为
,得 ,即 ,
因为 ,所以 ,即 ,故B错误;
因为 ,所以 ,
因为 为两切线的交点,
所以 ,
即 ,所以 ,所以 ,故C
正确;
因为 ,所以 ,所以 ,
同理得 ,得 ,即 ,
因为 ,所以 ,故D正确.
故选:ACD.
三、填空题:本大题共3小题,每小题5分,共15分,请把答案填写在答题卡相应位置上.
12. 方程 的解为_________.
【答案】6
【详解】根据题意, 或 ,且 ,
解得 .
故答案为:6.
13. 《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角
三角形的四面体称为鳖臑.如图,四面体 为鳖臑, 平面 , ,且
,则直线 与平面 所成角的大小为_________.【答案】 ##
【详解】取 的中点 ,连接 、 ,因为 , ,
所以 ,且 ,
又 平面 , 平面 ,所以 ,
因为 , 平面 ,
所以 平面 ,所以 直线 与平面 所成角,
又 平面 , 平面 ,所以 ,所以 ,
所以 ,则 ,
即直线 与平面 所成角的大小为 .
故答案为:14. 已知 ,则 _________.
【答案】
【详解】因为 ,所以 是含 项的系数,
若从 10 个 式子中取出 0 个 ,则需要从中取出 3 个 ,7 个 1,则得到的项为
;
若从 10 个 式子中取出 1 个 ,则需要从中取出 1 个 ,8 个 1,则得到的项为
;
若从10个 式子中取出大于或等于2个 ,则无法得到含 的项;
综上:含 的项为 ,则含 项的系数为 ,即 .
故答案为: .
四、解答题:本题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15. 已知10道试题中有4道选择题,甲、乙两人依次不放回地抽取1道,求:
(1)甲抽到选择题的概率;
(2)在甲抽到选择题的情况下,乙抽到选择题的概率.【答案】(1)
(2)
【小问1详解】
甲抽到选择题的概率为
【小问2详解】
在甲抽到选择题的情况下,乙抽到选择题的概率为 .
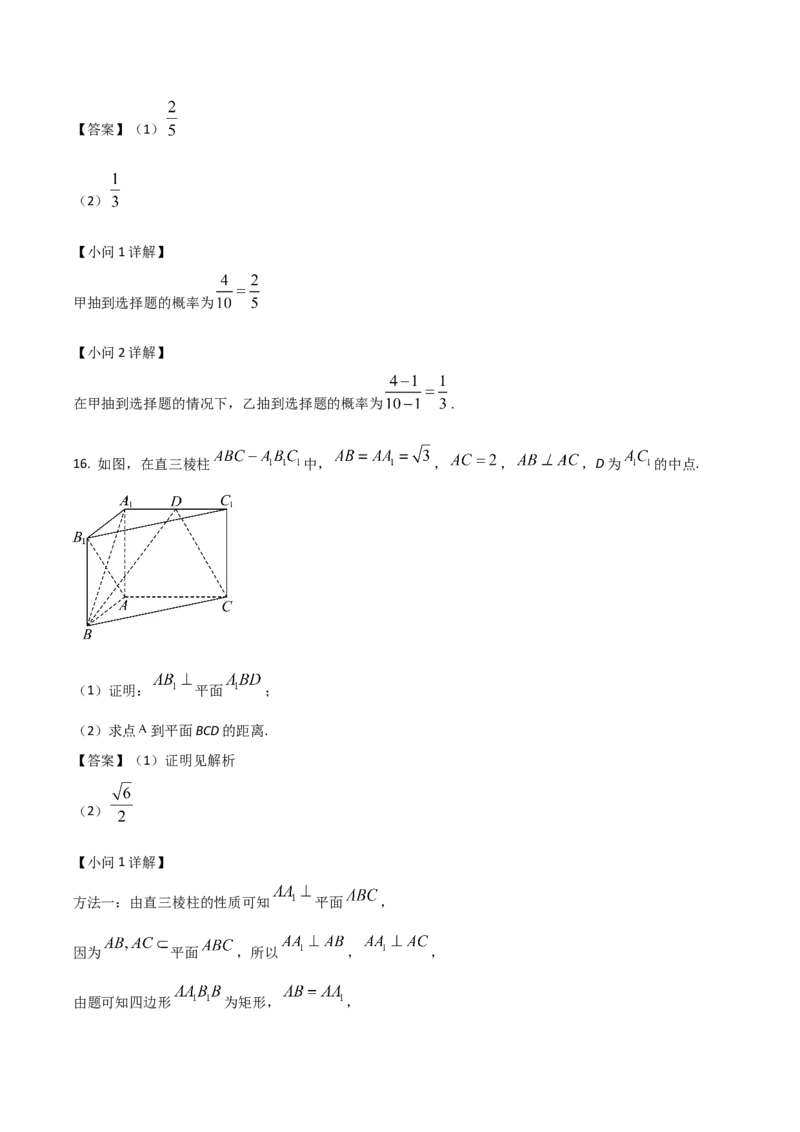
16. 如图,在直三棱柱 中, , , ,D为 的中点.
(1)证明: 平面 ;
(2)求点 到平面BCD的距离.
【答案】(1)证明见解析
(2)
【小问1详解】
方法一:由直三棱柱的性质可知 平面 ,
因为 平面 ,所以 , ,
由题可知四边形 为矩形, ,所以四边形 为正方形,所以 ,
因为 , , ,且 平面 ,
所以 平面 ,又 平面 ,
所以 ,因为 ,所以 ,
又因为 , , 平面 ,
所以 平面 .
方法二:以A为原点,AB,AC, 所在直线分别为 轴, 轴, 轴,
建立如图所示的空间直角坐标系,则 , , , , ,
,
则 , , ,
所以 ,
,
所以 , ,
又因为 , , 平面 ,所以 平面 .
【小问2详解】
的
方法一:设点 到平面BCD 距离为d,
易得 , , ,
则 ,则 ,
所以 ,
则 , ,
由 得, ,解得 ,
所以点A到平面BCD的距离为 .
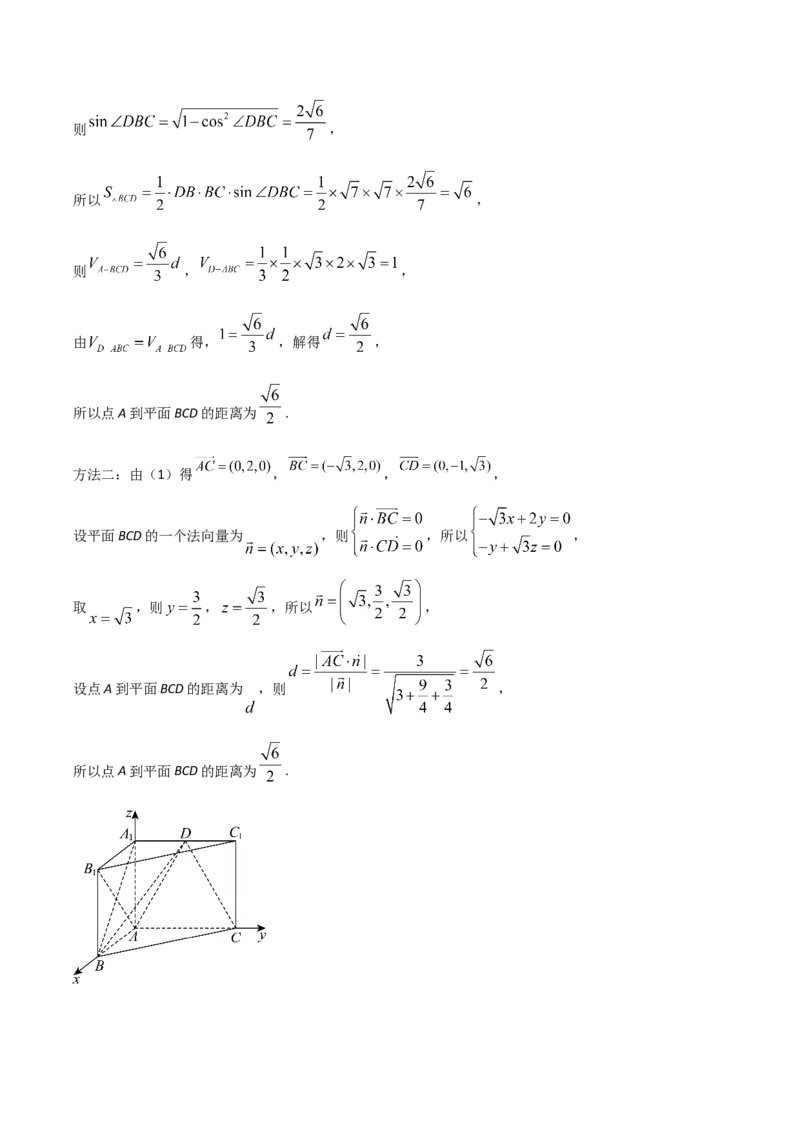
方法二:由(1)得 , , ,
设平面BCD的一个法向量为 ,则 ,所以 ,
取 ,则 , ,所以 ,
设点A到平面BCD的距离为 ,则 ,
所以点A到平面BCD的距离为 .17. 已知在 的展开式中,第2项与第3项的二项式系数之比是 .
(1)求展开式中的常数项,并指出是第几项;
(2)求展开式中的所有有理项.
【答案】(1) ,第5项;
(2) .
【小问1详解】
在 的展开式中,
第2项与第3项的二项式系数之比是 ,所以 .
所以展开式中的通项公式为 ,
令 ,得 ,所以常数项是第5项,为 .
【小问2详解】
由(1)可知,通项公式为 ,
令 ,则 ,
当 时, ,
当 时, ,
当 时, ,当 时, ,
故展开式中的所有有理项为: .
18. 如图,已知四棱台 的上、下底面分别是边长为2和4的正方形,平面 ⊥平
面ABCD, ,点P是棱 的中点,点Q在棱BC上.
(1)若 ,证明: 平面 ;
(2)若二面角 的正弦值为 ,求BQ的长.
【答案】(1)证明见解析;
(2)1.
【小问1详解】
证明:取 的中点M,连接MP,MB.
在四棱台 中,四边形 是梯形, , ,
又点M,P分别是棱 , 的中点,所以 ,且 .
在正方形ABCD中, , ,又 ,所以 .
从而 且 ,所以四边形BMPQ是平行四边形,所以 .又因为 平面 , 平面 ,所以 平面 ;
【小问2详解】
在平面 中,作 于O.
因为平面 平面 ,平面 平面 , , 平面
,
所以 平面 .
在正方形ABCD中,过O作AB的平行线交BC于点N,则 .
以 为正交基底,建立空间直角坐标系 .
因为四边形 是等腰梯形, , ,所以 ,又 ,所以
.
易得 , , , , ,所以 ,
, .法1:设 ,所以 .
设平面PDQ的法向量为 ,由 ,得 ,取 ,
另取平面DCQ的一个法向量为 .
设二面角 的平面角为θ,由题意得 .
又 ,所以 ,
解得 (舍负),因此 , .
所以当二面角 的正弦值为 时,BQ的长为1.
法2:设 ,所以 .
设平面PDQ的法向量为 ,由 ,得 ,取 ,
另取平面DCQ的一个法向量为 .
设二面角 的平面角为θ,由题意得 .又 ,所以 ,
解得 或6(舍),因此 .
所以当二面角 的正弦值为 时,BQ的长为1.
法3:在平面 中,作 ,垂足为H.
因为平面 平面 ,平面 平面 , , 平面
,
所以 平面 ,又 平面 ,所以 .
在平面ABCD中,作 ,垂足为G,连接PG.
因为 , , ,PH, 平面 ,
所以 平面 ,又 平面 ,所以 .
因为 , ,所以 是二面角 的平面角.
在四棱台 中,四边形 是梯形,
, , ,点P是棱 的中点,所以 , .
设 ,则 , ,
在 中, ,从而 .
因为二面角 的平面角与二面角 的平面角互补,
且二面角 的正弦值为 ,所以 ,从而 .
所以在 中, ,解得 或 (舍).
所以当二面角 的正弦值为 时,BQ的长为1.
19. 已知函数 , .
(1)若曲线 在 处的切线与直线 垂直,求 的值;
(2)讨论 的单调性;
(3)当 时, ,求 的取值范围.
【答案】(1)
(2)答案见解析 (3) .
【小问1详解】
因为 ,所以 ,所以 ,
又 在 处的切线与直线 垂直,所以 ,
即 ,所以 .
【小问2详解】
, .
①当 时, ,所以 在 上单调递增.
②当 时,令 ,得 ,又 ,所以 .
当 时, , 单调递减;当 时, , 单调递增.
综上,当 时, 在 上单调递增;
当 时, 在 上单调递减,在 上单调递增.
【小问3详解】
由 ,得 在 上恒成立.
令 , ,则 ,令 ,得 ,
当 时, , 单调递减;当 时, , 单调递增,
所以 ,即 ,则 在 上恒成立.
令 , ,
则
.
因为 ,所以 ,则 ,
令 ,得 ,
当 时, , 单调递减;当 时, , 单调递增,
所以 ,
所以 ,即 的取值范围是 .