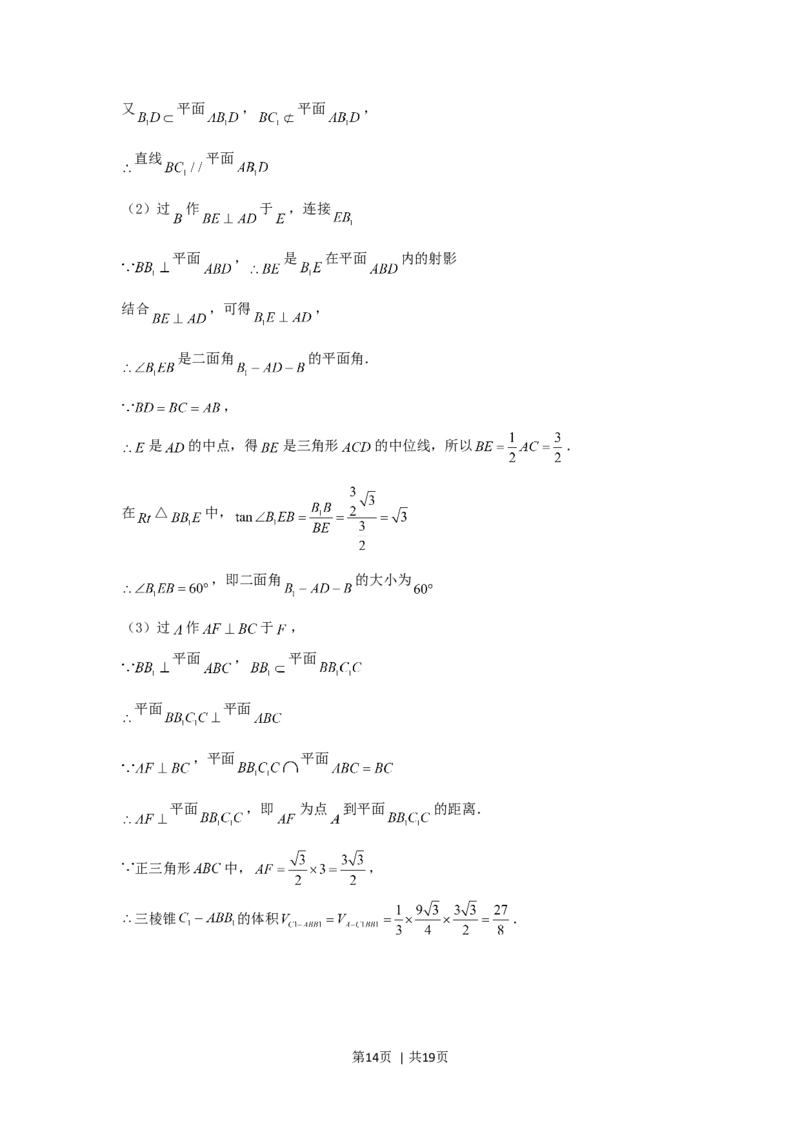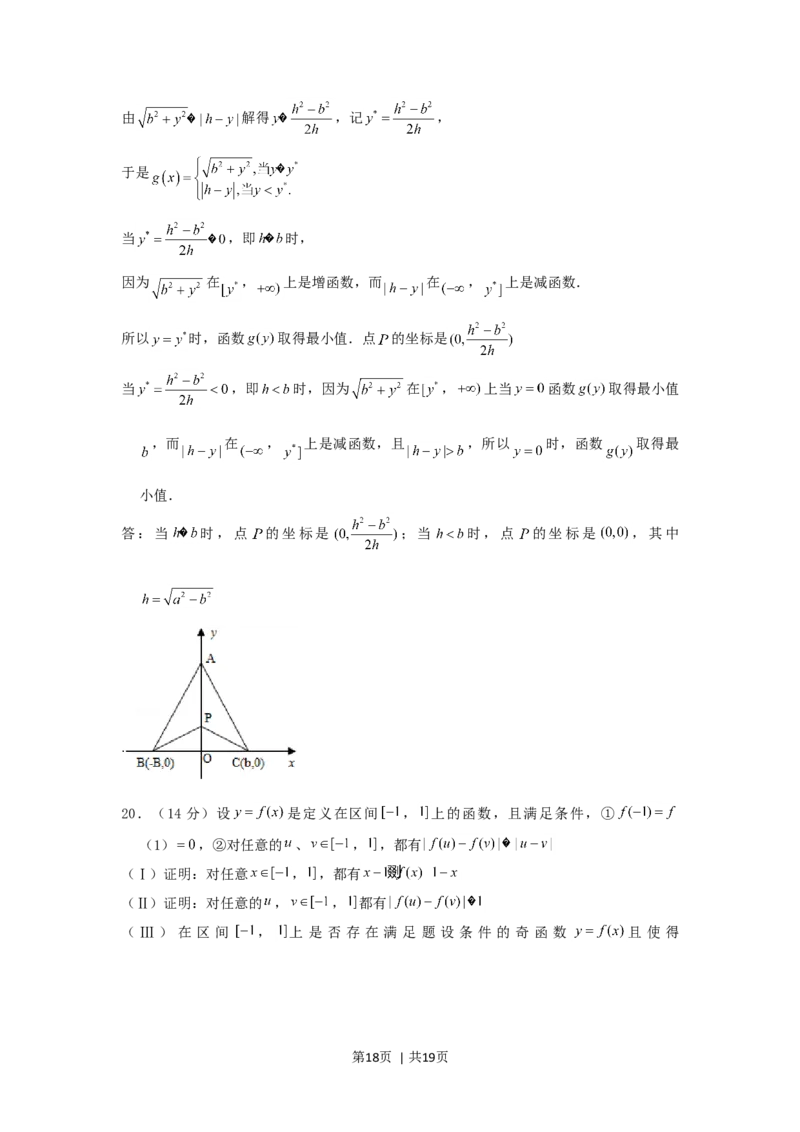文档内容
2003 年北京高考理科数学真题及答案
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合要求的.
1.(5分)设集合 , ,则 等于
A. B. C. D. 或
2.(5分)设 , , ,则
A. B. C. D.
3.(5分)“ ”是“ ”的
A.必要非充分条件 B.充分非必要条件
C.充分必要条件 D.既非充分又非必要条件
4.(5分)已知 , 是平面, , 是直线,下列命题中不正确的是
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
5.(5分)极坐标方程 表示的曲线是
A.圆 B.椭圆 C.抛物线 D.双曲线
6.(5分)若 ,且 ,则 的最小值是
A.2 B.3 C.4 D.5
7.(5分)如果圆台的母线与底面成 角,那么这个圆台的侧面积与轴截面面积的比为
A. B. C. D.
8.(5分)从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三
块土地上,其中黄瓜必须种植.不同的种植方法共有
A.24种 B.18种 C.12种 D.6种
9.(5分)若数列 的通项公式是 , ,2, ,则
第1页 | 共19页等于
A. B. C. D.
10.(5分)某班试用电子投票系统选举班干部候选人.全班 名同学都有选举权和被选
举权,他们的编号分别为1,2, , ,规定:同意按“1”,不同意(含弃权)按
“0”,令 其中 ,2, , ,且 ,2,
, ,则同时同意第1,2号同学当选的人数为
A.
B.
C.
D.
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
11.(4分)函数 , , 中, 是偶函
数.
12.(4分)已知双曲线方程为 ,则以双曲线左顶点为顶点,右焦点为焦点的
抛物线方程为 .
13.(4分)如图,已知底面半径为 的圆柱被一个平面所截,剩下部分母线长的最大值
为 ,最小值为 ,那么圆柱被截后剩下部分的体积是 .
14.(4分)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形
第2页 | 共19页与圆的面积之和最小,正方形的周长应为 .
三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)已知函数
(Ⅰ)求 的最小正周期;
(Ⅱ)求 在区间 上的最大值和最小值.
16.(13分)已知数列 是等差数列,且 , .
(1)求数列 的通项公式;
(2)令 ,求数列 前 项和的公式.
17.(15分)如图,三棱柱 的底面是边长为3的正三角形,侧棱 垂直于
底面 , , 是 延长线上一点,且 .
(1)求证:直线 平面 ;
(2)求二面角 的大小;
(3)求三棱锥 的体积.
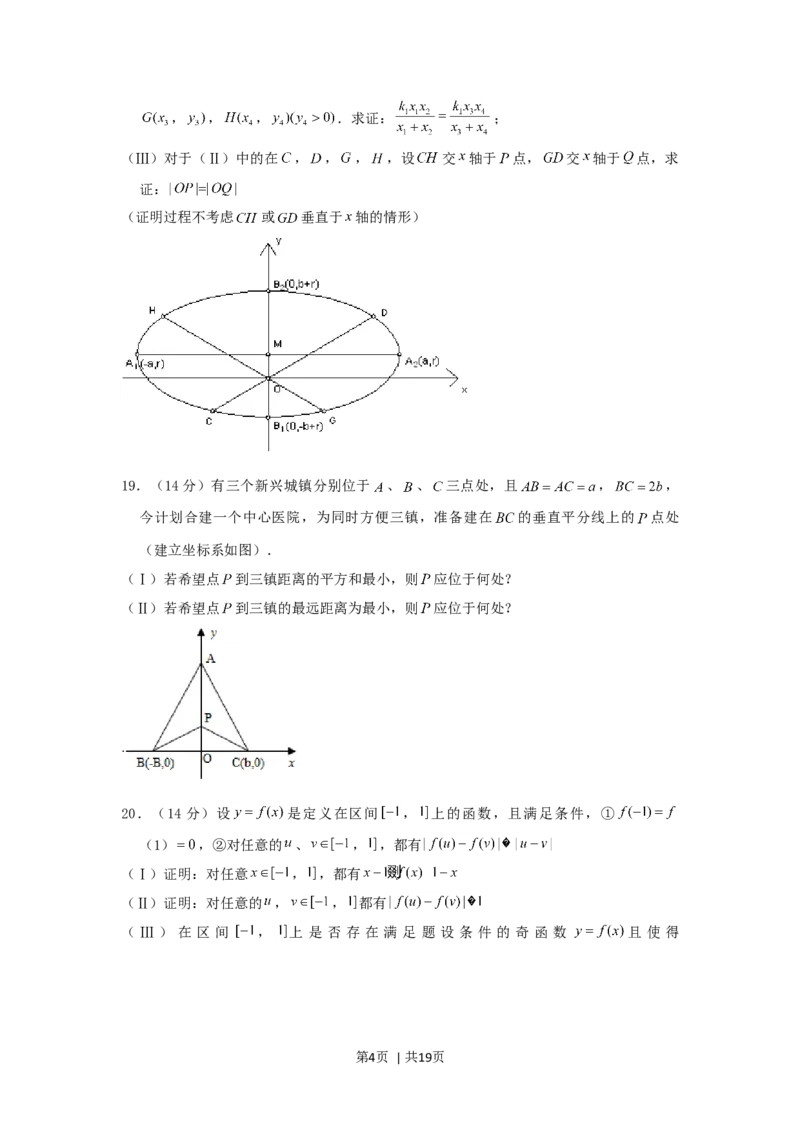
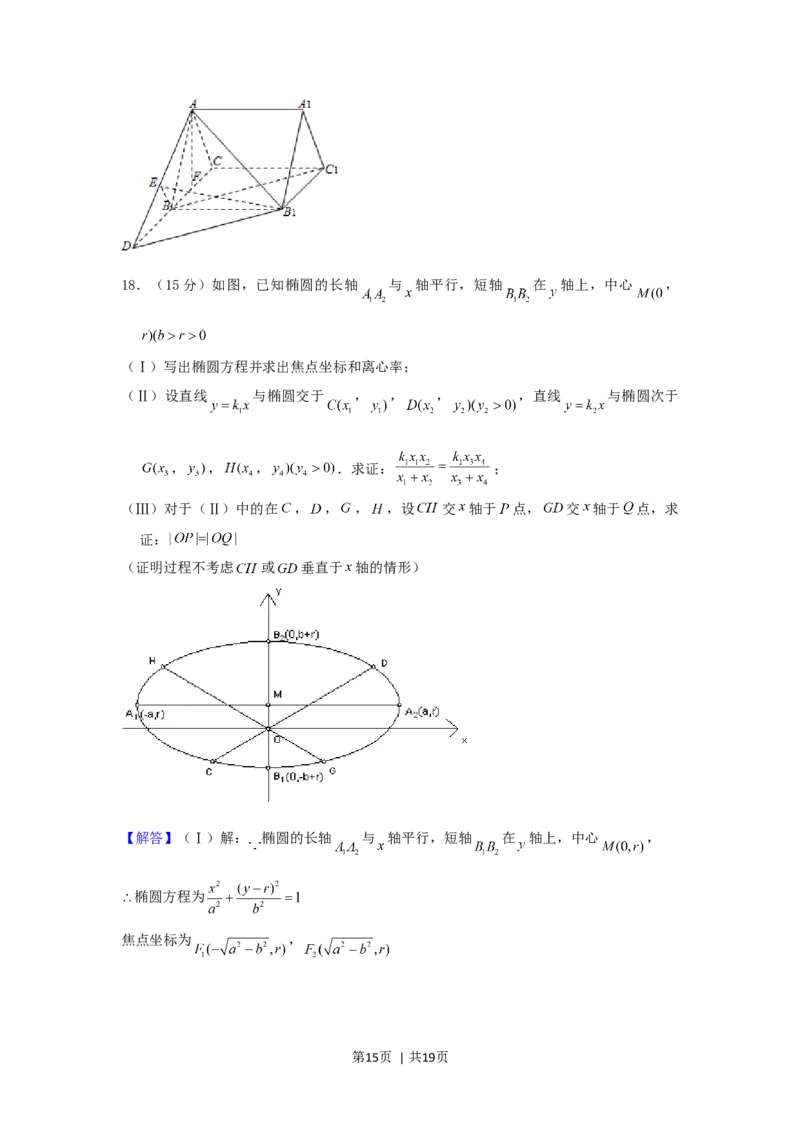
18.(15分)如图,已知椭圆的长轴 与 轴平行,短轴 在 轴上,中心 ,
(Ⅰ)写出椭圆方程并求出焦点坐标和离心率;
(Ⅱ)设直线 与椭圆交于 , , , ,直线 与椭圆次于
第3页 | 共19页, , , .求证: ;
(Ⅲ)对于(Ⅱ)中的在 , , , ,设 交 轴于 点, 交 轴于 点,求
证:
(证明过程不考虑 或 垂直于 轴的情形)
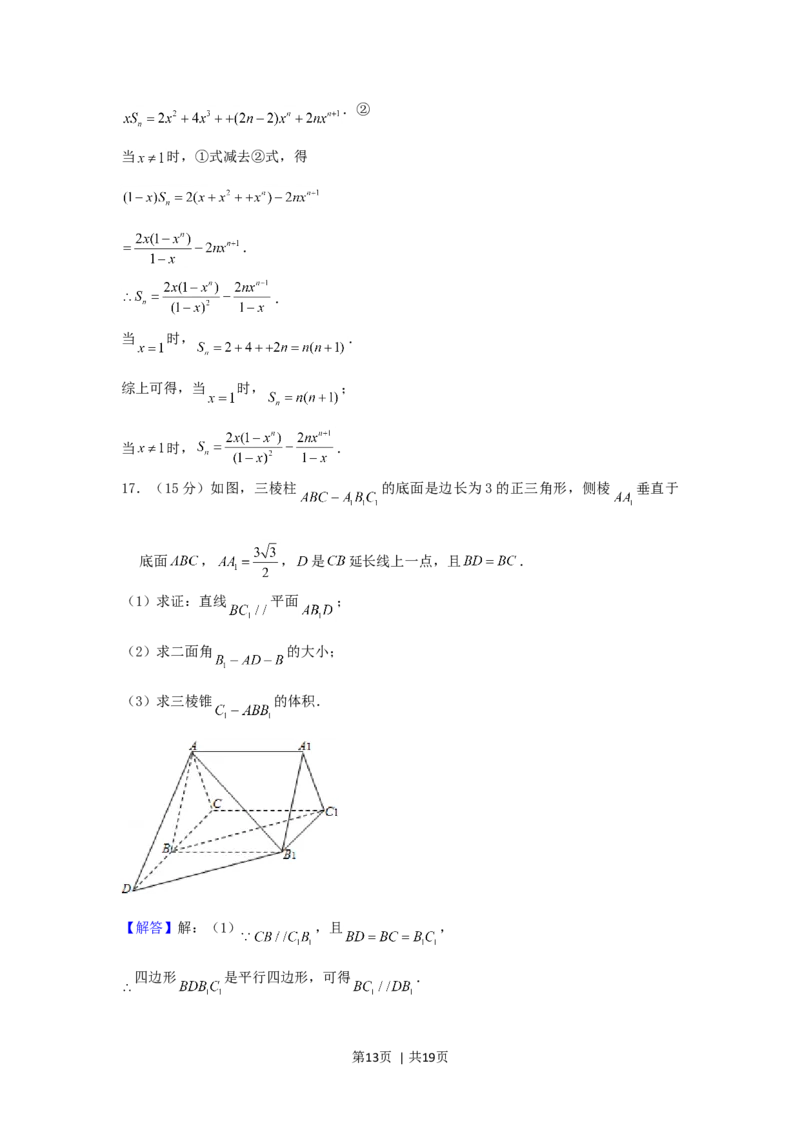
19.(14分)有三个新兴城镇分别位于 、 、 三点处,且 , ,
今计划合建一个中心医院,为同时方便三镇,准备建在 的垂直平分线上的 点处
(建立坐标系如图).
(Ⅰ)若希望点 到三镇距离的平方和最小,则 应位于何处?
(Ⅱ)若希望点 到三镇的最远距离为最小,则 应位于何处?
20.(14 分)设 是定义在区间 , 上的函数,且满足条件,①
(1) ,②对任意的 、 , ,都有
(Ⅰ)证明:对任意 , ,都有
(Ⅱ)证明:对任意的 , , 都有
( Ⅲ ) 在 区 间 , 上 是 否 存 在 满 足 题 设 条 件 的 奇 函 数 且 使 得
第4页 | 共19页;若存在请举一例,若不存在,请说明理由.
第5页 | 共19页一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合要求的.
1.(5分)设集合 , ,则 等于
A. B. C. D. 或
【解答】解:根据题意:集合 或 ,集合
.
故选: .
2.(5分)设 , , ,则
A. B. C. D.
【解答】解: , , .
因为函数 在定义域上为单调递增函数,所以 .
故选: .
3.(5分)“ ”是“ ”的
A.必要非充分条件 B.充分非必要条件
C.充分必要条件 D.既非充分又非必要条件
【解答】解:由 ,得 ,即 ,
所以 ,是“ ”的必要不充分条件.
故“ ”是“ ”的必要不充分条件.
故选: .
4.(5分)已知 , 是平面, , 是直线,下列命题中不正确的是
A.若 , ,则 B.若 , ,则
C.若 , ,则 D.若 , ,则
第6页 | 共19页【解答】解:对于 ,若 , , ,则
但条件中缺少“ ”,故不一定有 成立,故 不正确;
对于 ,根据两条平行线与同一个平面所成角相等,可得
若 , ,则 ,故 正确;
对于 ,根据垂直于同一条直线的两个平面互相平行,可得
若 , ,则 ,故 正确;
对于 ,若直线与平面垂直,则直线与平面内所有直线都垂直
故若 , ,则 ,故 正确
因此,不正确的命题只有
故选: .
5.(5分)极坐标方程 表示的曲线是
A.圆 B.椭圆 C.抛物线 D.双曲线
【解答】解:极坐标方程 可化为: ,
,即 ,它表示中心在 的双曲线.
极坐标方程 表示的曲线是双曲线.
故选: .
6.(5分)若 ,且 ,则 的最小值是
A.2 B.3 C.4 D.5
【解答】解:由题意知, 表示:复平面上的点到 的距离为1的圆,
即以 为圆心,以1为半径的圆,
表示:圆上的点到 的距离的最小值,
即圆心 到 的距离减去半径1,
则
故选: .
7.(5分)如果圆台的母线与底面成 角,那么这个圆台的侧面积与轴截面面积的比为
A. B. C. D.
【解答】解: 圆台的母线与底面成 角,
第7页 | 共19页设上底圆半径为 ,下底面圆半径为 ,母线为 ,可得
因此,圆台的侧面积为
又 圆台的高
圆台的轴截面面积为
由此可得圆台的侧面积与轴截面面积的比为
故选: .
8.(5分)从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三
块土地上,其中黄瓜必须种植.不同的种植方法共有
A.24种 B.18种 C.12种 D.6种
【解答】解: 黄瓜必选,故再选2种蔬菜的方法数是 种,
在不同土质的三块土地上种植的方法是 ,
种法共有 种,
故选: .
9.(5分)若数列 的通项公式是 , ,2, ,则
等于
A. B. C. D.
【解答】解:
第8页 | 共19页即
.
.,
故选: .
10.(5分)某班试用电子投票系统选举班干部候选人.全班 名同学都有选举权和被选
举权,他们的编号分别为1,2, , ,规定:同意按“1”,不同意(含弃权)按
“0”,令 其中 ,2, , ,且 ,2,
, ,则同时同意第1,2号同学当选的人数为
A.
B.
C.
D.
【解答】解:第1,2, , 名学生是否同意第1号同学当选依次由 , , , ,
来确定 表示同意, 表示不同意或弃权),是否同意第2号同学当选依次
由 , , , 确定,
而是否同时同意1,2号同学当选依次由 , , , 确定,
故同时同意1,2号同学当选的人数为 ,
故选: .
第9页 | 共19页二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上.
11.(4 分)函数 , , 中, 、
是偶函数.
【解答】解: ,
为偶函数.
又 当 时, ,
.
又 , .
当 时, ,
.
又 , .
当 时, ,
.
又 , .
综上,对任意 都有 .
为偶函数.
,
为奇函数.
12.(4分)已知双曲线方程为 ,则以双曲线左顶点为顶点,右焦点为焦点的
抛物线方程为 .
【解答】解:根据双曲线方程可知 ,
,
左顶点坐标为 ,右焦点坐标为 ,
抛物线顶点为双曲线的左顶点,焦点为右焦点,
,焦点在顶点的右侧,在 轴上
抛物线方程 .
第10页 | 共19页故答案为: .
13.(4分)如图,已知底面半径为 的圆柱被一个平面所截,剩下部分母线长的最大值
为 ,最小值为 ,那么圆柱被截后剩下部分的体积是 .
【解答】解:取两个相同的几何体,倒立一个,对应合缝,恰好形成一个圆柱体.
所求几何体的体积:
故答案为:
14.(4分)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形
与圆的面积之和最小,正方形的周长应为 .
【解答】解析:设正方形周长为 ,则圆的周长为 ,半径 .
, .
.
当 时有最小值.
答案:
三、解答题:本大题共6小题,共84分.解答应写出文字说明,证明过程或演算步骤.
15.(13分)已知函数
(Ⅰ)求 的最小正周期;
(Ⅱ)求 在区间 上的最大值和最小值.
第11页 | 共19页【解答】解:(Ⅰ)由题意知,
的最小正周期 .
(Ⅱ) ,
当 时, 取最大值为 ,
当 时, 取最小值为
的最大值为1,最小值为
16.(13分)已知数列 是等差数列,且 , .
(1)求数列 的通项公式;
(2)令 ,求数列 前 项和的公式.
【解答】解:(1)设数列 的公差为 ,
则 .
又 ,得 .
.
(2)当 时, , ,
当 时,令 ,
则由 ,得
,①
第12页 | 共19页.②
当 时,①式减去②式,得
.
.
当 时, .
综上可得,当 时, ;
当 时, .
17.(15分)如图,三棱柱 的底面是边长为3的正三角形,侧棱 垂直于
底面 , , 是 延长线上一点,且 .
(1)求证:直线 平面 ;
(2)求二面角 的大小;
(3)求三棱锥 的体积.
【解答】解:(1) ,且 ,
四边形 是平行四边形,可得 .
第13页 | 共19页又 平面 , 平面 ,
直线 平面
(2)过 作 于 ,连接
平面 , 是 在平面 内的射影
结合 ,可得 ,
是二面角 的平面角.
,
是 的中点,得 是三角形 的中位线,所以 .
在 △ 中,
,即二面角 的大小为
(3)过 作 于 ,
平面 , 平面
平面 平面
,平面 平面
平面 ,即 为点 到平面 的距离.
正三角形 中, ,
三棱锥 的体积 .
第14页 | 共19页18.(15分)如图,已知椭圆的长轴 与 轴平行,短轴 在 轴上,中心 ,
(Ⅰ)写出椭圆方程并求出焦点坐标和离心率;
(Ⅱ)设直线 与椭圆交于 , , , ,直线 与椭圆次于
, , , .求证: ;
(Ⅲ)对于(Ⅱ)中的在 , , , ,设 交 轴于 点, 交 轴于 点,求
证:
(证明过程不考虑 或 垂直于 轴的情形)
【解答】(Ⅰ)解: 椭圆的长轴 与 轴平行,短轴 在 轴上,中心 ,
椭圆方程为
焦点坐标为 ,
第15页 | 共19页离心率
( Ⅱ ) 证 明 : 将 直 线 的 方 程 代 入 椭 圆 方 程 , 得
整理得
根据韦达定理,得 , ,
所以 ①
将直线 的方程 代入椭圆方程 ,同理可得 ②
由 ①、②得
所以结论成立
(Ⅲ)证明:设点 ,点
由 、 、 共线,得
解得
由 、 、 共线,同理可得
由 变形得
所以
即
第16页 | 共19页19.(14分)有三个新兴城镇分别位于 、 、 三点处,且 , ,
今计划合建一个中心医院,为同时方便三镇,准备建在 的垂直平分线上的 点处
(建立坐标系如图).
(Ⅰ)若希望点 到三镇距离的平方和最小,则 应位于何处?
(Ⅱ)若希望点 到三镇的最远距离为最小,则 应位于何处?
【解答】解:(Ⅰ)由题设条件 ,设 的坐标为 ,则 至三镇距离的平方
和为
所以,当 时,函数 取得最小值.
答:点 的坐标是
(Ⅱ)记
至三镇的最远距离为
第17页 | 共19页由 解得 ,记 ,
于是
当 ,即 时,
因为 在 , 上是增函数,而 在 , 上是减函数.
所以 时,函数 取得最小值.点 的坐标是
当 ,即 时,因为 在 , 上当 函数 取得最小值
,而 在 , 上是减函数,且 ,所以 时,函数 取得最
小值.
答:当 时,点 的坐标是 ;当 时,点 的坐标是 ,其中
20.(14 分)设 是定义在区间 , 上的函数,且满足条件,①
(1) ,②对任意的 、 , ,都有
(Ⅰ)证明:对任意 , ,都有
(Ⅱ)证明:对任意的 , , 都有
( Ⅲ ) 在 区 间 , 上 是 否 存 在 满 足 题 设 条 件 的 奇 函 数 且 使 得
第18页 | 共19页;若存在请举一例,若不存在,请说明理由.
【解答】(Ⅰ)证明:由题设条件可知,
当 , 时,有 (1) ,即 .
(Ⅱ)证明:对任意的 , , ,
当 时,有
当 时, ,不妨设 , , , ,则
从而有 (1)
综上可知,对任意的 , , ,都有
(Ⅲ)解:这样满足所述条件的函数不存在.理由如下:
假设存在函数 满足条件,则由 .
得
又 (1) ,所以 ①
又因为 为奇函数,所以 ,
由条件 .
得
所以 ②
①与②矛盾,因此假设不成立,即这样的函数不存在.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/5/27 22:54:30;用户:15217760367;邮箱:15217760367;学号:10888156
第19页 | 共19页