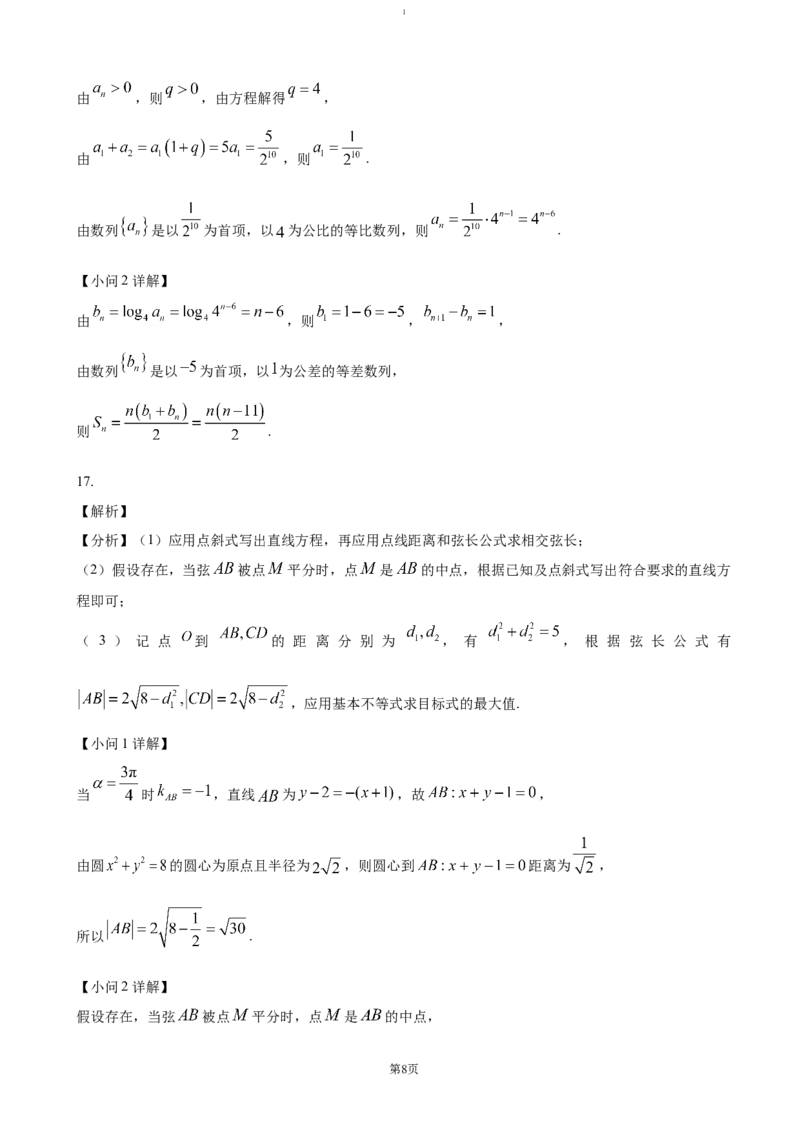文档内容
1
2024~2025 学年度第一学期阶段联测
高二数学试题
(考试时间120分钟总分150分)
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1. 已知直线 与 垂直,则 ()
A0 B. 1 C. 2 D.
2. 双曲线 的焦点到渐近线的距离为()
A. B. 2 C. D.
3. 已知数列1, , , ,3,…,按此规律, 是该数列的()
A. 第11项 B. 第12项 C. 第13项 D. 第14项
4. 以点 为圆心,且与直线 相切的圆的方程是()
A. B.
C. D.
5. 已知点 ,抛物线 上有一点 ,则 的最小值是()
A. 10 B. 8 C. 5 D. 4
6. “天问一号”是执行中国首次火星探测任务的探测器,该名称源于屈原长诗《天问》,寓意探求科学真理
征途漫漫,追求科技创新永无止境.图(1)是“天问一号”探测器环绕火星的椭圆轨道示意图,火星的球心
是椭圆的一个焦点.过椭圆上的点P向火星被椭圆轨道平面截得的大圆作两条切线 ,则
就是“天问一号”在点P时对火星的观测角.图(2)所示的Q,R,S,T四个点处,对火星的观测角最大的
是()
第1页1
A. Q B. R C. S D. T
7. 将正整数 分解为两个正整数 、 的积,即 ,当 、 两数差的绝对值最小时,我们称其
为最优分解.如 ,其中 即为20的最优分解,当 、 是 的最优分解时,
定义 ,则数列 的前2024项的和为()
A. B. C. D.
的
8. 已知 是圆 一条弦, , 是 的中点.当弦 在圆 上运动时,
直线 上总存在两点 , ,使得 为钝角,则 的取值范围是()
A. B. C. D.
二、多项选择题:本大题共3小题,每小题6分,共18分.全对得6分,部分对得部分分.
9. 已知曲线 ,下列说法正确的是()
A. 若 ,则曲线C为椭圆
B. 若 ,则曲线C为双曲线
C. 若曲线C为椭圆,则其长轴长一定大于2
D. 若曲线C为焦点在x轴上的双曲线,则其离心率小于 大于1
10. 已知数列 满足 , ,则下列说法正确的是()
第2页1
A. B. 中存在连续三项成等差数列
C. 中存在连续三项成等比数列 D. 数列 的前 项和
11. 已知椭圆 的左、右顶点分别为 , ,左、右焦点分别为 , , 是椭
圆 上异于 , 的一点,且 ( 为坐标原点),记 , 的斜率分别为 , ,
设 为 的内心,记 , , 的面积分别为 , , ,则()
A. B. 的离心率为 C. D.
三、填空题:本题共3小题,每小题5分,共15分.
12. 下列条件中,哪两个条件组合一定能得到抛物线的标准方程为 的是______(填序号)(写出一
个正确答案即可).
①焦点在 轴上;②焦点在 轴上;③抛物线上横坐标为 的点到焦点的距离为 ;④焦点到准线的距离为
;⑤由原点向过焦点的某直线作垂线,垂足坐标为 .
13. 已知数列 满足, ,且 .若 是数列 的前 项积,求 的最大值为______.
14. 如图所示,已知双曲线 的右焦点F,过点F作直线l交双曲线C于 两
点,过点F作直线l的垂线交双曲线C于点G, ,且三点 共线(其中O为坐标原
点),则双曲线C的离心率为_________.
第3页1
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15. 已知双曲线 的离心率 ,实轴长 .
(1)求 的方程;
的
(2)过 右焦点且倾斜角为 的直线交 于 , 两点,求 ;
16. 在等比数列 中, , , .
(1)求数列 的通项公式;
(2)设 ,求数列 的前 项和 ;
17. 如图,圆 内有一点 , 为过点 且倾斜角为 的弦.
(1)当 时,求 的长;
(2)是否存在弦 被点 平分?若存在,写出直线 的方程;若不存在,请说明理由.
(3) 是过点 的另一条弦,当 与 始终保持垂直时,求 的最大值.
18. 已知椭圆 的一个焦点 ,两个焦点与短轴的一个端点构成等边三角形.
第4页1
(1)求椭圆 的标准方程;
(2)过焦点 作 轴的垂线交椭圆上半部分于点 ,过点 作椭圆 的弦 在椭圆上
且直线 的倾斜角互补,问直线MN的斜率是否为定值?若是,求出这个定值;若不是,请说明
理由.
(3)在第(2)问的条件下,当 面积最大时,求直线MN的方程.
19. 若数列 满足 ( 为正整数, 为常数),则称数列 为等方差数列, 为公方差.
(1)已知数列 , 的通项公式分别为: , ,判断上述两个数列是否为等方
差数列,并说明理由;
(2)若数列 既是等方差数列,又是等差数列,证明:数列 为常数列.
(3)若数列 是首项为1,公方差为2的等方差数列,在(1)的条件下,在 与 之间依次插入数
列 中的 项构成新数列 : , , , , , , , , , ,……,求数列
中前30项的和 .
2024~2025 学年度第一学期阶段联测
高二数学试题
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
第5页1
1.
【答案】C
2.
【答案】B
3.
【答案】D
4.
【答案】D
5.
【答案】B
6.
【答案】A
7.
【答案】B
8.
【答案】D
二、多项选择题:本大题共3小题,每小题6分,共18分.全对得6分,部分对得部分分.
9.
【答案】BCD
10.
【答案】ABD
11.
【答案】ACD
三、填空题:本题共3小题,每小题5分,共15分.
12.
【答案】①③(答案不唯一)
13.
【答案】
14.
【答案】
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.
第6页1
【解析】
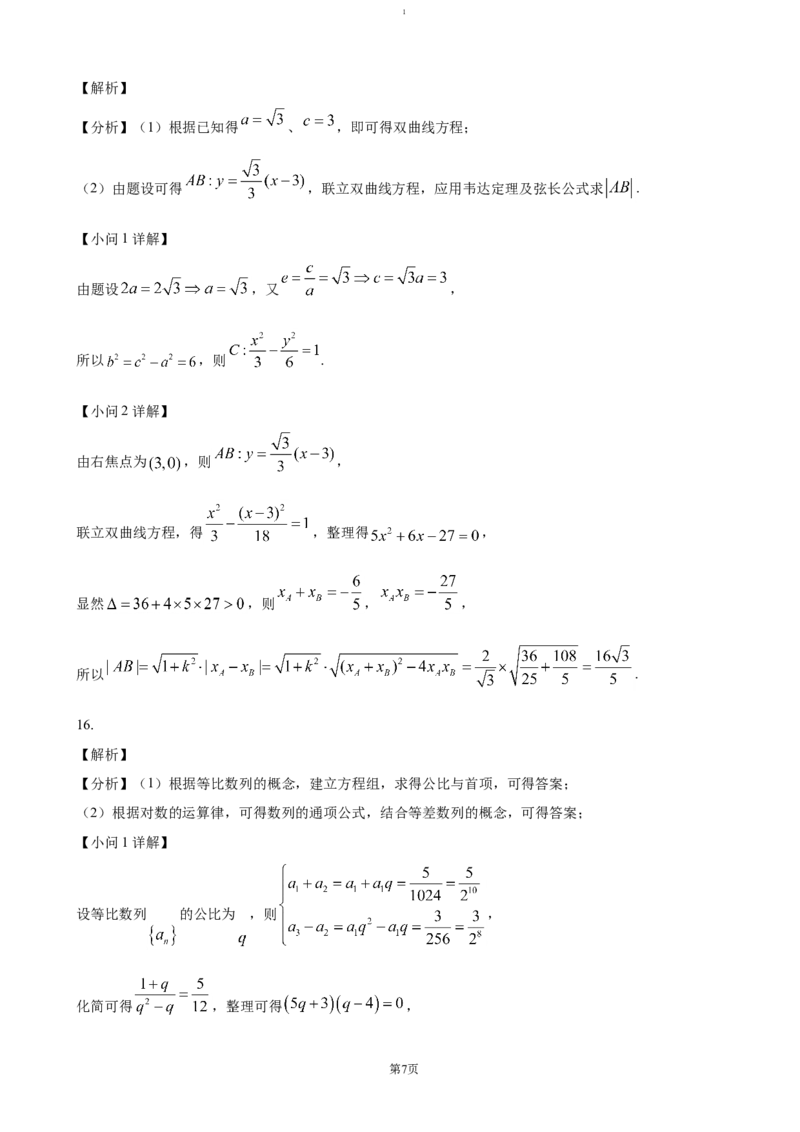
【分析】(1)根据已知得 、 ,即可得双曲线方程;
(2)由题设可得 ,联立双曲线方程,应用韦达定理及弦长公式求 .
【小问1详解】
由题设 ,又 ,
所以 ,则 .
【小问2详解】
由右焦点为 ,则 ,
联立双曲线方程,得 ,整理得 ,
显然 ,则 , ,
所以 .
16.
【解析】
【分析】(1)根据等比数列的概念,建立方程组,求得公比与首项,可得答案;
(2)根据对数的运算律,可得数列的通项公式,结合等差数列的概念,可得答案;
【小问1详解】
设等比数列 的公比为 ,则 ,
化简可得 ,整理可得 ,
第7页1
由 ,则 ,由方程解得 ,
由 ,则 .
由数列 是以 为首项,以 为公比的等比数列,则 .
【小问2详解】
由 ,则 , ,
由数列 是以 为首项,以 为公差的等差数列,
则 .
17.
【解析】
【分析】(1)应用点斜式写出直线方程,再应用点线距离和弦长公式求相交弦长;
(2)假设存在,当弦 被点 平分时,点 是 的中点,根据已知及点斜式写出符合要求的直线方
程即可;
( 3 ) 记 点 到 的 距 离 分 别 为 , 有 , 根 据 弦 长 公 式 有
,应用基本不等式求目标式的最大值.
【小问1详解】
当 时 ,直线 为 ,故 ,
由圆 的圆心为原点且半径为 ,则圆心到 距离为 ,
所以 .
【小问2详解】
假设存在,当弦 被点 平分时,点 是 的中点,
第8页1
连接 ,则 ,故 ,又 ,即 ,
所以直线 为 ,则 .
【小问3详解】
记点 到 的距离分别为 ,有 ,
又 ,
,
当且仅当 时等号成立,
综上, 的最大值为 .
18.
【解析】
【分析】(1)根据题意,易得 的值,进而分析可得 ,由公式求出 ,代入椭圆方程即得;
(2)根据题意,设直线PM方程,将其与椭圆方程联立,由根与系数的关系得 的坐标,利用PM与PN
的关系,得 的坐标,然后利用斜率的计算公式化简计算即得.
(3)由原点 到直线的距离及弦长公式可求出面积,利用二次函数求出最值即得直线的方程.
【小问1详解】
由题意可知椭圆的半焦距 ,
第9页1
由两个焦点与短轴的一个端点构成等边三角形得 ,
,
故椭圆 的标准方程为 .
【小问2详解】
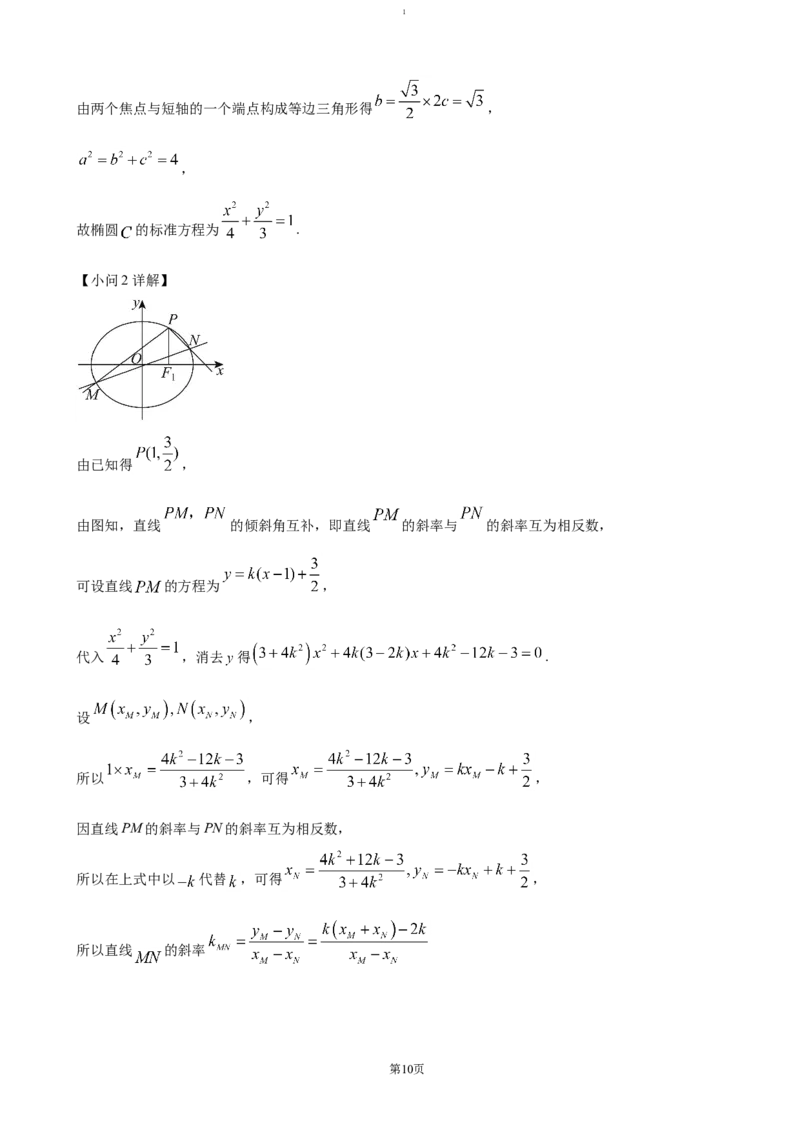
由已知得 ,
由图知,直线 的倾斜角互补,即直线 的斜率与 的斜率互为相反数,
可设直线 的方程为 ,
代入 ,消去 得 .
设 ,
所以 ,可得 ,
因直线PM的斜率与PN的斜率互为相反数,
所以在上式中以 代替 ,可得 ,
所以直线 的斜率
第10页1
,
即直线 的斜率为定值 .
【小问3详解】
由(1)已得, ,可设直线 的方程为: ,
代入 ,整理得: ,
则 ,即 ,
设 ,则 ,
于是, ,
点 到直线 的距离为 ,
则 的面积为:
,
因 ,则 ,故当 时, 取得最大值 ,
此时直线 的方程为 ,
即 和 .
19.
【解析】
【分析】(1)根据等方差数列的定义,即可判断;
第11页1
(2)根据等差数列及等方差数列的定义即可求解;
(3)首先说明 是等比数列,再根据等比数列和等差数列求和公式,即可求解.
【小问1详解】
因为 常数 ,
所以数列 为等方差数列,1为公方差;
为
因 ,
所以数列 不是等方差数列;
【小问2详解】
因为 是等差数列,设其公差为d,
则 ,
又 是等方差数列,所以 ,
故 ,
所以 ,
即 ,
所以 ,故 是常数列;
【小问3详解】
由题意知数列 是首项为1,公方差为2的等方差数列,
故 ,而 ,所以 ,
是首项为1,公比为3的等比数列,
而新数列 中 项 含 前共有 项,
第12页1
令 ,结合 ,解得 ,
故数列 中前30项含有 的前7项和数列 的前23项,
所以数列 中前30项的和 .
第13页