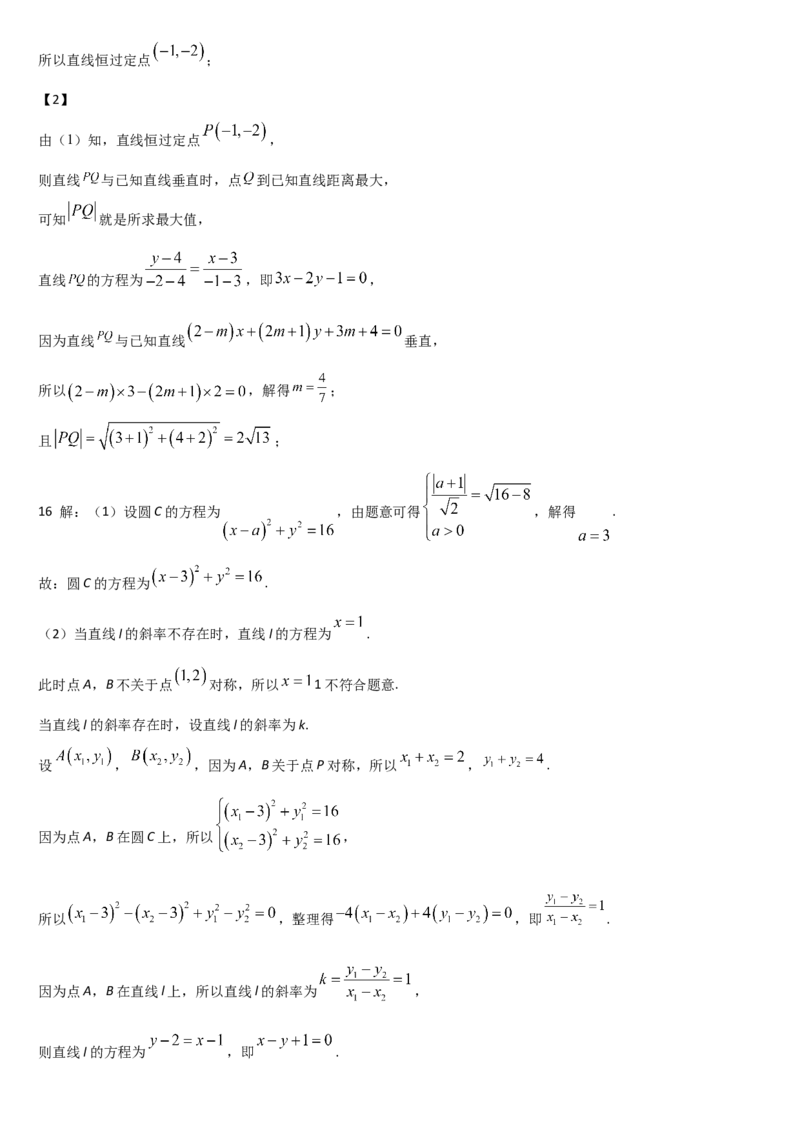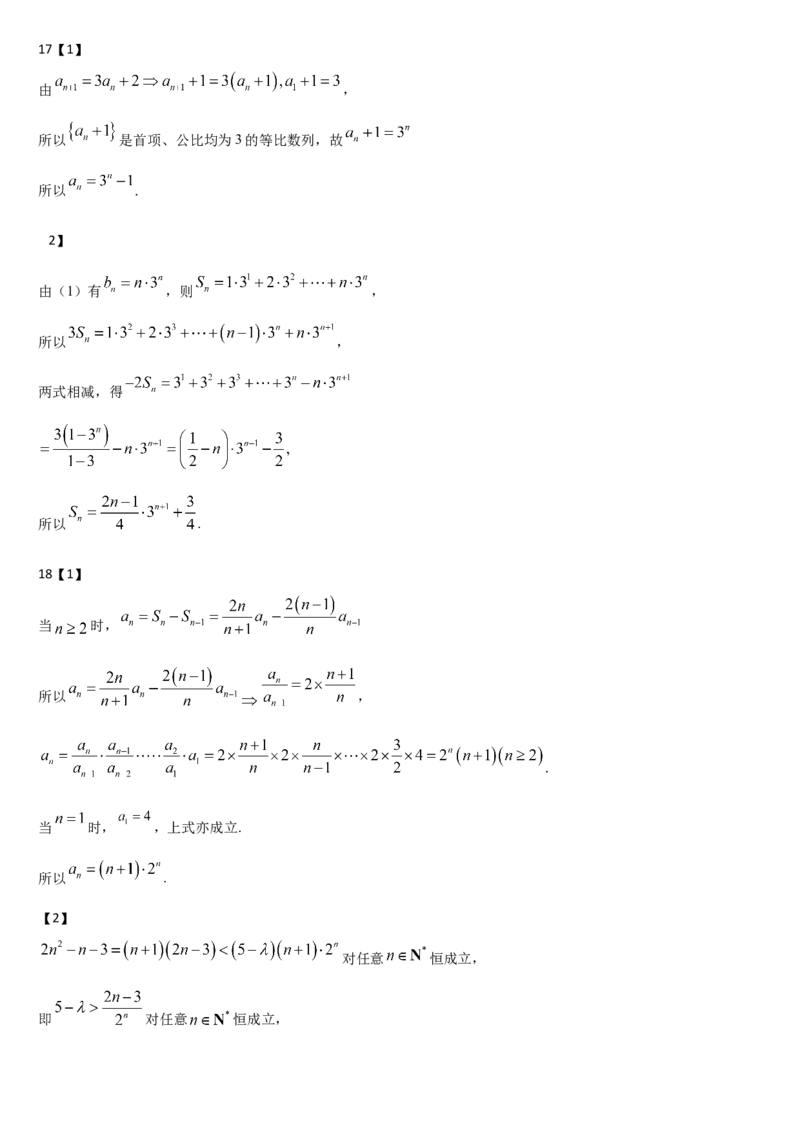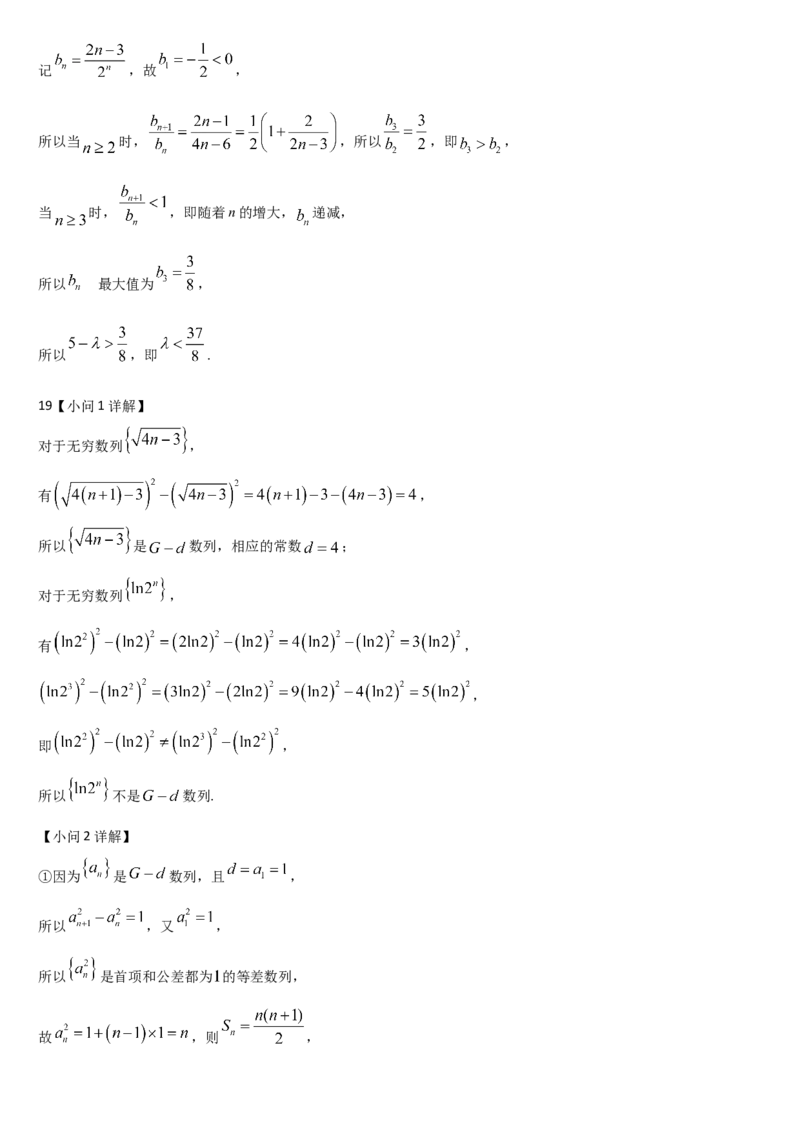文档内容
高二数学 12 月考
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1. 已知空间向量 , ,若 ,则 ( )
A. 4 B. 6 C. D.
2. 二项式 展开式的常数项为( )
A. B. 60 C. 120 D. 240
3. 2024年第二届贵州“村超”总决赛阶段的比赛正式拉开帷幕某校足球社的6名学生准备分成三组前往村超球队所在的
平地村、口寨村、忠诚村3个村寨进行调研,每个村各有一组来调研,每个组至多3名学生,则不同的安排方法种数为
( )
A. 900 B. 600 C. 450 D. 150
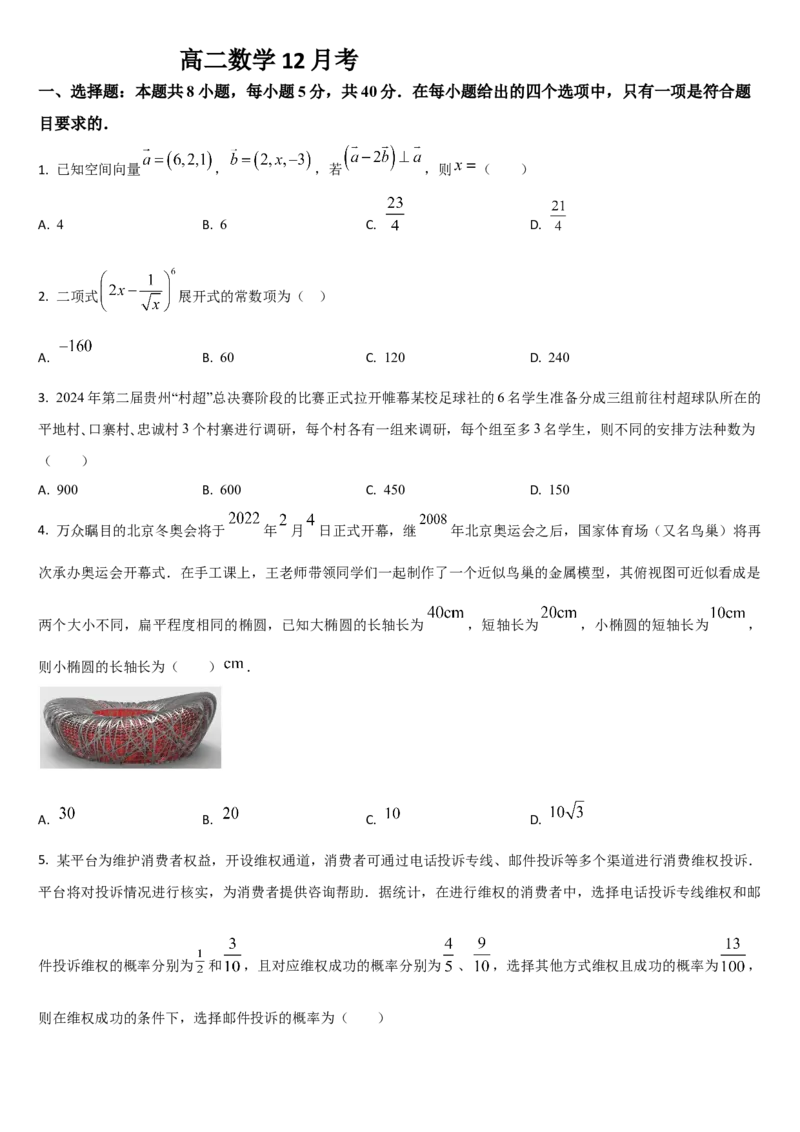
4. 万众瞩目的北京冬奥会将于 年 月 日正式开幕,继 年北京奥运会之后,国家体育场(又名鸟巢)将再
次承办奥运会开幕式.在手工课上,王老师带领同学们一起制作了一个近似鸟巢的金属模型,其俯视图可近似看成是
两个大小不同,扁平程度相同的椭圆,已知大椭圆的长轴长为 ,短轴长为 ,小椭圆的短轴长为 ,
则小椭圆的长轴长为( ) .
A. B. C. D.
5. 某平台为维护消费者权益,开设维权通道,消费者可通过电话投诉专线、邮件投诉等多个渠道进行消费维权投诉.
平台将对投诉情况进行核实,为消费者提供咨询帮助.据统计,在进行维权的消费者中,选择电话投诉专线维权和邮
件投诉维权的概率分别为 和 ,且对应维权成功的概率分别为 、 ,选择其他方式维权且成功的概率为 ,
则在维权成功的条件下,选择邮件投诉的概率为( )A. B. C. D.
的
6. 已知三棱锥 顶点都在球 的球面上,底面 为等边三角形,且其所在圆 的面积为 .若三棱
锥 的体积的最大值为 ,则球 的体积为( )
A. B. C. D.
7. 已知双曲线 ,左右焦点分别为 ,过 作平行于 的渐近线的直线交 于点 ,
若 ,则 的离心率为( )
A. B. C. D.
8. 已知点P在直线l: 上,过点P的两条直线与圆O: 分别相切于A,B两点,则圆心O到
直线AB的距离的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多个选项是符合
题目要求的,全部选对的得6分,部分选的得部分分,有选错的得0分.
9. 已知函数 ,则下列说法正确的是( )
A. 函数 的最小正周期为
B. 函数 在区间 上单调递增
C. 函数 的图象的对称轴方程为
D. 函数 的图象可由函数 的图象向右平移 个单位长度得到
10. 已知实数 满足方程 ,则下列说法正确的是( )A. 的最大值为 B. 的最大值为
C. 的最大值为 D. 的最大值为
11. 已知点 ,点P是双曲线C: 左支上的动点, 为其右焦点,N是圆D: 的动
点,直线 交双曲线右支于Q(O为坐标原点),则( )
A. B. 过点M作与双曲线C仅有一个公共点的直线恰有2条
C. 的最小值为 D. 若 的内切圆E与圆D外切,则圆E的半径为
三、填空题(共3题,每题5分,共15分)
12. 已知直线 平面 ,且直线 的方向向量为 ,平面 的法向量为 ,则 _____.
13. 已知直线 与圆 相交于 两点,则 ___________.
14. 设双曲线 : 的左、右焦点分别为 ,以 为圆心的圆恰好与双曲线 的两渐近
线相切,且该圆过线段 的中点,则双曲线 的离心率是_____.
四、解答题(共5题,共77分)
15. 已知直线方程为 .
(1)证明:直线恒过定点,并求定点坐标;
(2) 为何值时,点 到直线的距离最大,并求最大值.
16. 已知圆C的圆心C在x轴的正半轴上,半径为4,直线 被圆C截得的弦长为 .
(1)求圆C的方程;
(2)已知直线l过点 ,且与圆C交于A,B两点.若A,B关于点P对称,求直线l的方程.
.
17 已知数列 满足 .
(1)证明:数列 是等比数列,并求数列 的通项公式;(2)设 ,求数列 的前 项和 .
18. 已知数列 的前n项和 ,且 .
(1)求数列 的通项公式;
(2)若不等式 对任意 恒成立,求 的取值范围.
19. 对于各项均为正数 无的穷数列 ,若 ,都有 ,其中 为非零常数,则称数列 是
数列.
(1)判断无穷数列 和 是不是 数列?若是,求出相应的常数 的值;若不是,请说明理由;
(2)若 是数列,且 ,
①记 的前 项和为 ,求证: ;
②对任意的正整数 ,设 ,求数列 的前 项和.
CBCBB BDC 9AC 10AB 11ACD 12
## 13 14 ##
15【1】
由直线方程 得
,
因为 ,所以 ,解得 ,所以直线恒过定点 ;
【2】
由(1)知,直线恒过定点 ,
则直线 与已知直线垂直时,点 到已知直线距离最大,
可知 就是所求最大值,
直线 的方程为 ,即 ,
因为直线 与已知直线 垂直,
所以 ,解得 ;
且 ;
16 解:(1)设圆C的方程为 ,由题意可得 ,解得 .
故:圆C的方程为 .
(2)当直线l的斜率不存在时,直线l的方程为 .
此时点A,B不关于点 对称,所以 1不符合题意.
当直线l的斜率存在时,设直线l的斜率为k.
设 , ,因为A,B关于点P对称,所以 , .
因为点A,B在圆C上,所以 ,
所以 ,整理得 ,即 .
因为点A,B在直线l上,所以直线l的斜率为 ,
则直线l的方程为 ,即 .17【1】
由 ,
所以 是首项、公比均为3的等比数列,故
所以 .
【
2】
由(1)有 ,则 ,
所以 ,
两式相减,得
所以 .
18【1】
当 时,
所以 ,
.
当 时, ,上式亦成立.
所以 .
【2】
对任意 恒成立,
即 对任意 恒成立,记 ,故 ,
所以当 时, ,所以 ,即 ,
当 时, ,即随着n的增大, 递减,
所以 的最大值为 ,
所以 ,即 .
19【小问1详解】
对于无穷数列 ,
有 ,
所以 是 数列,相应的常数 ;
对于无穷数列 ,
有 ,
,
即 ,
所以 不是 数列.
【小问2详解】
①因为 是 数列,且 ,
所以 ,又 ,
所以 是首项和公差都为 的等差数列,
故 ,则 ,故 , ,
从而
,
因为 ,所以 ,则 ,
所以 ,即 ;
②当n为奇数时, ,
当n为偶数时, ,
所以 ,
而 ,
则 ,
两式相减,得 ,
,
所以 ,
因此 .所以数列 的前2n项和为 .