2004年湖北高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_湖北

2004 年湖北高考文科数学真题及答案 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题 目要求的. 1．设A{x| x  5k 1,kN),B{x| x 6,xQ},则AB等于 （ ） A．{1,4} B．{1,6} C．{4,6} D．{1,4,6} 2．已知点M（6，2）和M（1，7）.直线y=mx—7与线段MM 的交点M分有向线段MM 的比为3：2，则m的 2 1 2 1 2 值为 （ ） 3 2 1 A． B． C． D．4 2 3 4 3．已知函数 f(x)在x 1处的导数为3,则f(x)的解析式可能为 （ ） A． f(x) (x1)2 3(x1) B． f(x)  2(x1) C． f(x)  2(x1)2 D． f(x)  x1 4．两个圆C :x2  y2 2x2y20与C :x2  y2 4x2y10的公切线有且仅有 1 2 （ ） A．1条 B．2条 C．3条 D．4条 5．若函数 f(x)  ax b1(a 0且a 1)的图象经过第二、三、四象限，则一定有（ ） A．0 a 1且b 0 B．a 1且b 0 C．0 a 1且b 0 D．a 1且b0 6．四面体ABCD四个面的重心分别为E、F、G、H，则四面体EFGH的表面积与四面体ABCD的表面积的比值 是 （ ） 1 1 1 1 A． B． C． D． 27 16 9 8 7．已知a,b,c为非零的平面向量. 甲：ab  ac,乙:b c,则 （ ） A．甲是乙的充分条件但不是必要条件 B．甲是乙的必要条件但不是充分条件 C．甲是乙的充要条件 D．甲既不是乙的充分条件也不是乙的必要条件 5 x2 4x5 8．已知x  ,则f(x)  有 （ ） 2 2x4 5 5 A．最大值 B．最小值 C．最大值1 D．最小值1 4 4 1 1 9．已知数列{a }的前n项和S  a[2( )n1]b[2(n1)( )n1](n 1,2, ),其中a、b是非零常数， n n 2 2  则存在数列{x }、{y }使得 （ ） n n 第1页 | 共9页A．a  x  y ,其中{x }为等差数列，{y }为等比数列 n n n n n B．a  x  y ,其中{x }和{y }都为等差数列 n n n n n C．a  x  y ,其中{x }为等差数列，{y }都为等比数列 n n n n n D．a  x  y ,其中{x }和{y }都为等比数列 n n n n n 1 1 10．若1  ,则下列结论中不正确的是 （ ） a b A．log b log a B．|log blog a| 2 a b a b C．(log a)2 1 D．|log b||log a||log blog a| b a b a b 11．将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子里，每个盒内放一个球，恰 好3个球的标号与其在盒子的标号不一致的放入方法种数为（ ） A．120 B．240 C．360 D．720 12．设 y  f(t)是某港口水的深度y（米）关于时间t（时）的函数，其中0t  24.下表是该港口某一 天从0时至24时记录的时间t与水深y的关系： t 0 3 6 9 12 15 18 21 24 y 12 15.1 12.1 9.1 11.9 14.9 11.9 8.9 12.1 经长期观观察，函数y  f(t)的图象可以近似地看成函数y  k  Asin(t )的图象.在下面的函数 中，最能近似表示表中数据间对应关系的函数是 （ ）   A．y 123sin t,t[0,24] B．y 123sin( t ),t[0,24] 6 6    C．y 123sin t,t[0,24] D．y 123sin( t  ),t[0,24] 12 12 2 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13．Tan2010°的值为 . 1 1  14．已知(x2  x 2)n的展开式中各项系数的和是128，则展开式中x5的系数是 .（以数字作答） 15．某校有老师200人，男学生1200人，女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量 为n的样本；已知从女学生中抽取的人数为80人，则n= . 16．设A、B为两个集合，下列四个命题： ①A B对任意xA,有xB ②A B A B   ③A BA B ④A B存在xA,使得xB 其中真命题的序号是 .（把符合要求的命题序号都填上） 三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分） 第2页 | 共9页  已知6sin2sincos2cos20,[ ,],求sin(2 )的值. 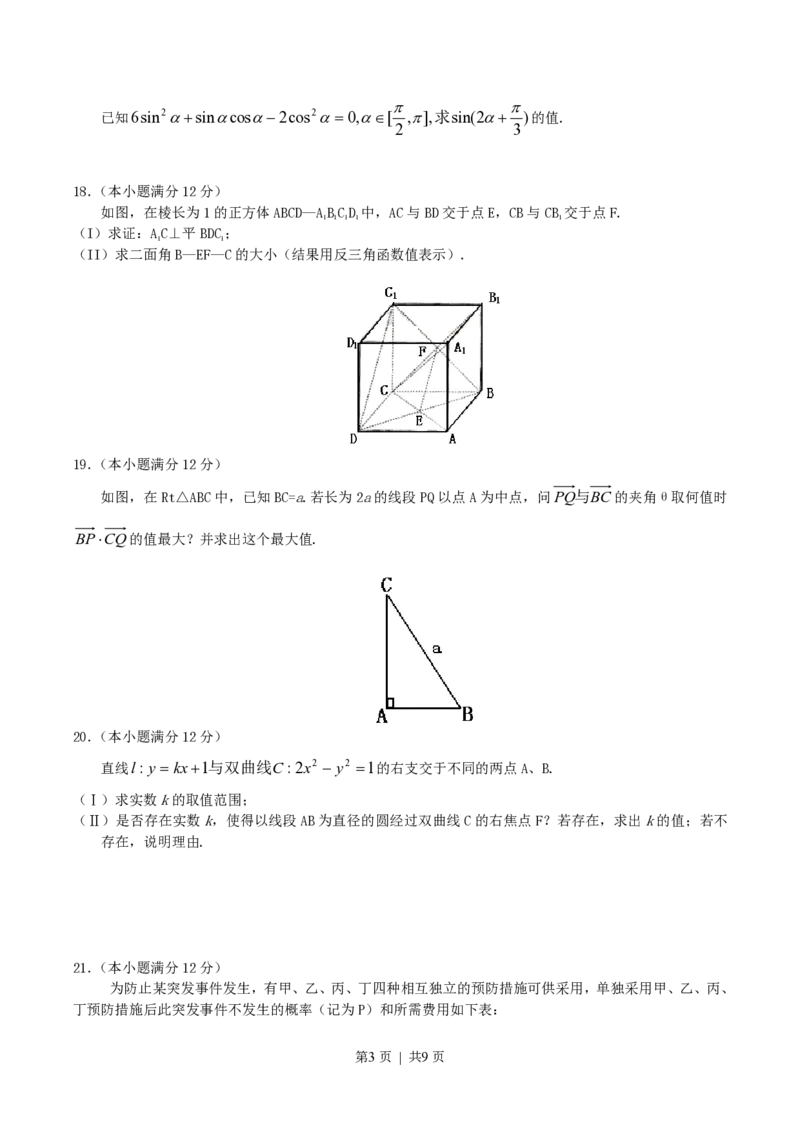2 3 18．（本小题满分12分） 如图，在棱长为1的正方体ABCD—ABCD 中，AC与BD交于点E，CB与CB 交于点F. 1 1 1 1 1 （I）求证：AC⊥平BDC； 1 1 （II）求二面角B—EF—C的大小（结果用反三角函数值表示）. 19．（本小题满分12分） 如图，在Rt△ABC中，已知BC=a.若长为2a的线段PQ以点A为中点，问PQ与BC的夹角θ取何值时 BPCQ的值最大？并求出这个最大值. 20．（本小题满分12分） 直线l: y  kx1与双曲线C:2x2  y2 1的右支交于不同的两点A、B. （Ⅰ）求实数k的取值范围； （Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？若存在，求出k的值；若不 存在，说明理由. 21．（本小题满分12分） 为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施可供采用，单独采用甲、乙、丙、 丁预防措施后此突发事件不发生的概率（记为P）和所需费用如下表： 第3页 | 共9页预防措施 甲 乙 丙 丁 P 0.9 0.8 0.7 0.6 费用（万元） 90 60 30 10 预防方案可单独采用一种预防措施或联合采用几种预防措施，在总费用不超过120万元的前提下，请 确定一个预防方案，使得此突发事件不发生的概率最大. 22．（本小题满分14分） 已知b  1,c 0,函数f(x)  xb的图象与函数g(x)  x2 bxc的图象相切. （Ⅰ）求b与c的关系式（用c表示b）； （Ⅱ）设函数F(x)  f(x)g(x)在(,)内有极值点，求c的取值范围. 2004年普通高等学校招生全国统一考试 数学（文史类（湖北卷）参考答案 一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题 目要求的. 1．D 2．D 3．A 4．B 5．C 6．C 7．B 8．D 9．C 10．D 11．B 12．A 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 第4页 | 共9页3 13． 14．35 15．192 16．④ 3 17．本小题考三角函数的基本公式以及三角函数式的恒等基础知识和基本运算技能，满分12分. 解法一：由已知得：(3sin2cos)(2sincos) 0  3sin2cos0或2sincos0   由已知条件可知cos 0,所以 ,即( ,). 2 2 2 于是tan0,tan  . 3    sin(2 ) sin2cos cos2sin 3 3 3 3 sincos (cos2sin2) 2 sincos 3 cos2sin2    cos2sin2 2 cos2sin2 tan 3 1tan2    . 1tan2 2 1tan2 2 将tan  代入上式得 3 2 2 ( ) 1( )2  3 3 3 sin(2 )     3 2 2 2 1( )2 1( )2 3 3 6 5    3.即为所求. 13 26  解法二：由已知条件可知cos 0,则a  ,所以原式可化为 2 6tan2tan20. 即(3tan2)(2tan1) 0.  又 ( ,),tan0.  2 2 tan  . 3 下同解法一. 18．本小题主要考查线面关系和正方体等基础知识，考查空间想象能力和推理能力.满分12分. 解法一：（Ⅰ）∵AA⊥底面ABCD，则AC是AC在底面ABCD的射影. 1 1 ∵AC⊥BD.∴AC⊥BD. 1 同理AC⊥DC,又BD∩DC=D, 1 1 1 ∴AC⊥平面BDC 1 1. 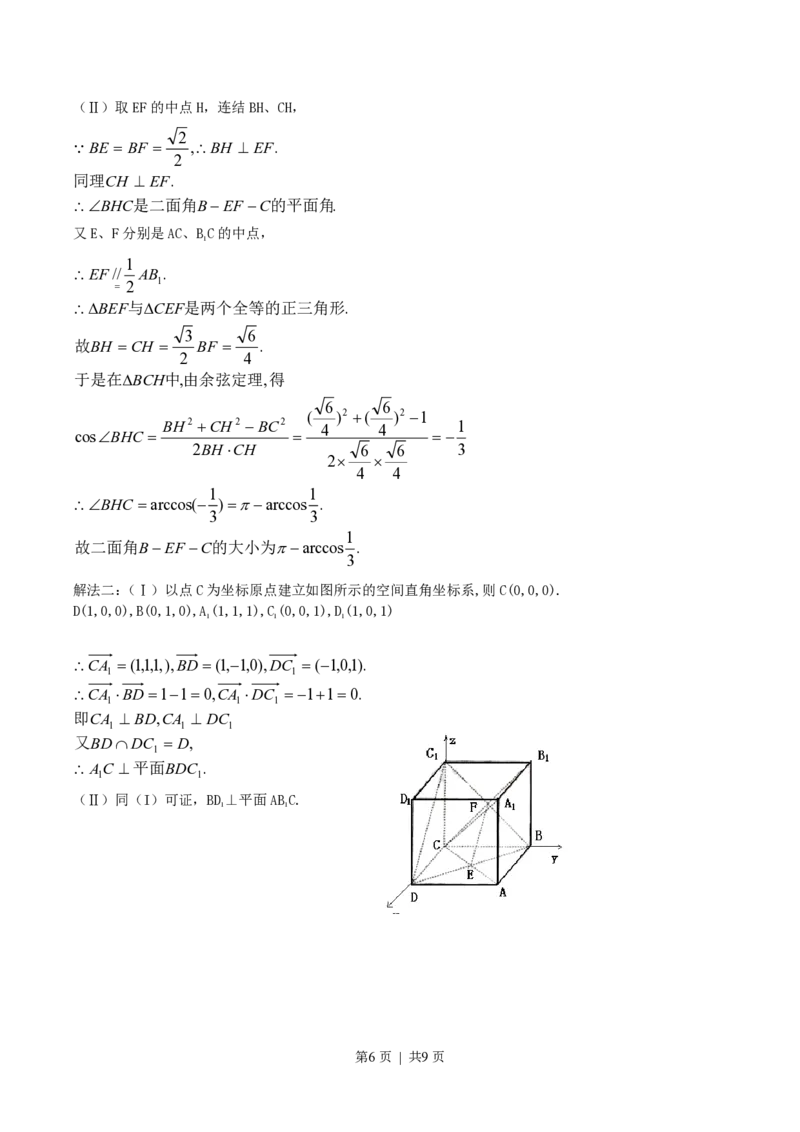第5页 | 共9页（Ⅱ）取EF的中点H，连结BH、CH， 2 BE  BF  ,BH  EF.  2 同理CH  EF. BHC是二面角BEF C的平面角. 又E、F分别是AC、BC的中点， 1 1 EF// AB .  2 1 BEF与CEF是两个全等的正三角形. 3 6 故BH CH  BF  . 2 4 于是在BCH中,由余弦定理,得 6 6 ( )2 ( )2 1 BH2 CH2 BC2 4 4 1 cosBHC     2BH CH 6 6 3 2  4 4 1 1 BHC arccos( ) arccos . 3 3 1 故二面角BEF C的大小为arccos . 3 解法二：（Ⅰ）以点C为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0). D(1,0,0),B(0,1,0),A(1,1,1),C(0,0,1),D(1,0,1) 1 1 1 CA (1,1,1,),BD (1,1,0),DC (1,0,1). 1 1 CA BD 110,CA DC  110. 1 1 1 即CA  BD,CA  DC 1 1 1 又BDDC  D, 1 AC 平面BDC . 1 1 （Ⅱ）同（I）可证，BD⊥平面ABC. 1 1 第6页 | 共9页则 A D,D B 就是所求二面角 1 1 的平面角补角的大小. AC (1,1,1),D B (1,1,1),  1 1 ACD B cos AC,D B  1 1 1 1 | AC || D B| 1 1 1 1   . 3 3 3 1 故二面角BEF C的大小为arccos . 3 19．本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力，满分12分. 解法一: AB  AC,ABAC 0.  AP  AQ,BP  AP AB,CQ  AQ AC,  BPCQ (AP AB)(AQ AC)  APAQ APAC  ABAQ ABAC  a3  APAC  ABAP  a2  AP(AB AC) 1  a2  PQBC 2  a2 a2 cos. 故当cos1,即0(PQ与BC方向相同)时,BPCQ最大.其最大值为0. 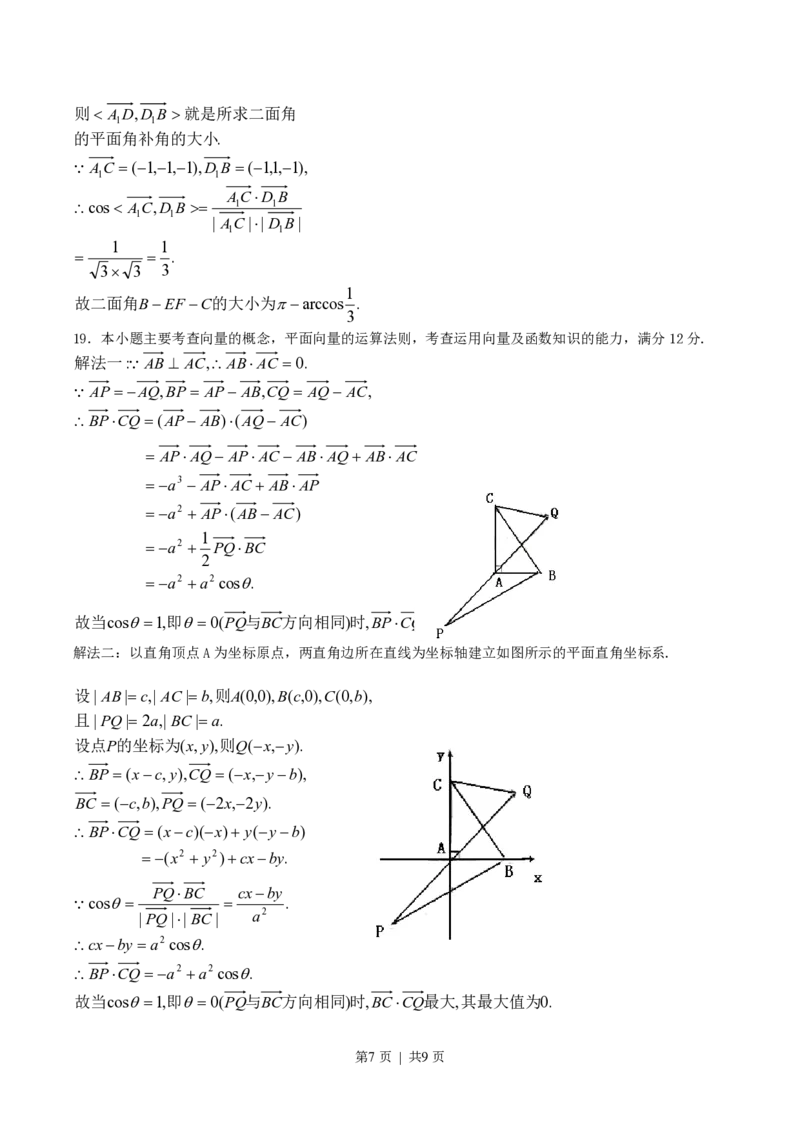解法二：以直角顶点A为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系. 设| AB|c,| AC |b,则A(0,0),B(c,0),C(0,b), 且| PQ| 2a,| BC | a. 设点P的坐标为(x,y),则Q(x,y). BP (xc,y),CQ (x,yb), BC (c,b),PQ (2x,2y). BPCQ (xc)(x) y(yb)  (x2  y2)cxby. PQBC cxby cos  .  | PQ|| BC | a2 cxby  a2 cos. BPCQ  a2 a2 cos. 故当cos1,即0(PQ与BC方向相同)时,BCCQ最大,其最大值为0. 第7页 | 共9页20．本小题主要考查直线、双曲线的方程和性质，曲线与方程的关系，及其综合应用能力，满分12分. 解：（Ⅰ）将直线l的方程y  kx1代入双曲线C的方程2x2  y2 1后,整理得 (k2 2)x2 2kx20.……① 依题意，直线l与双曲线C的右支交于不同两点，故 k2 2 0,   (2k)2 8(k2 2) 0,  2k  0  k2 2  2  0. k2 2 解得k的取值范围是2 k   2. （Ⅱ）设A、B两点的坐标分别为(x ,y )、(x ,y )，则由①式得 1 1 2 2  2k x  x  ,   1 2 2k2  ……② 2  x x  .   2 2 k2 2 假设存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F（c,0）. 则由FA⊥FB得： (x c)(x c) y y 0. 1 2 1 2 即(x c)(x c)(kx 1)(kx 1) 0. 1 2 1 2 整理得 (k2 1)x x (k c)(x  x )c2 10.……③ 1 2 1 2 6 把②式及c  代入③式化简得 2 5k2 2 6k 60. 6 6 6 6 解得k   或k  (2, 2)(舍去). 5 5 6 6 可知k   使得以AB为直径的圆经过双曲线C的右焦点. 5 21．本小题考查概率的基础知识以及运用概率知识解决 实际问题的能力，满分12分. 解：方案1：单独采用一种预防措施的费用均不超过120万元.由表可知，采用甲措施，可使此突发事件不 发生的概率最大，其概率为0.9. 方案2：联合采用两种预防措施，费用不超过120万元，由表可知.联合甲、丙两种预防措施可使此突发事 件不发生的概率最大，其概率为 1—(1—0.9)(1—0.7)=0.97. 第8页 | 共9页方法3：联合采用三种预防措施，费用不超过120万元，故只能联合乙、丙、丁三种预防措施，此时突发事 件不发生的概率为 1—（1—0.8）(1—0.7)(1—0.6)=1—0.024=0.976. 综合上述三种预防方案可知，在总费用不超过120万元的前提下，联合使用乙、丙、丁三种预防措施可使 此突发事件不发生的概率最大. 22．本小题考查导数、切线、极值等知识及综合运用数学知识解决问题的能力.满分14分. 1b 解：（Ⅰ）依题意，令 f (x)  g(x),得2xb 1,故x  . 2 1b 12b 由于f( )  g( ),得(b1)2  4c. 2 2 b  1,c 0,b  12 c.  （Ⅱ）F(x)  f(x)g(x)  x3 2bx2 (b2 c)xbc.F(x) 3x2 4bxb2 c. 令F(x) 0,即3x2 4bxb2 c 0. 则 16b2 12(b2 c)  4(b2 3c). 若 0,则F(x) 0有一个实根x ,且F(x)的变化如下: 0 x (,x ) x （x ,) 0 0 0 F(x) + 0 + 于是x  x 不是函数F(x)的极值点. 0 若 0,则F(x) 0有两个不相等的实根x ,x (x  x )且F(x)的变化如下： 1 2 1 2 x (,x ) x (x ,x ) x （x ,) 1 1 1 2 2 2 F(x) + 0 — 0 + 由此，x  x 是函数F(x)的极大值点,x  x 是函数F(x)的极小值点. 1 2 综上所述，当且仅当 0时,函数F(x)在(,)上有极值点. 由  4(b2 3c) 0得b  3c或b  3c. b  12 c,12 c  3c或12 c  3c.  解之得0c 74 3或c 74 3. 故所求c的取值范围是(0,74 3)(74 3,). 第9页 | 共9页