文档内容
莆田第二十五中学 2023-2024 学年上学期高三数学期中考试卷
考试时间:120分钟
一、单项选择题(本大题共8小题,每小题5分,共40分)
1. 已知集合 或 ,则 ( )
A. B. C. D.
2. “若 , 恒成立”是真命题,则实数 可能取值是( )
.
A B. C. 4 D. 5
3. 华罗庚说:“数无形时少直觉,形少数时难入微,数与形,本是相倚依,焉能分作两边飞.”所以研究函
数时往往要作图,那么函数 的部分图象可能是( )
A. B.
C. D.
4. 若一系列函数的解析式和值域相同,但定义域不相同,则称这些函数为“同值函数”.例如函数 ,
与函数 , 即为“同值函数”,给出下面四个函数,其中能够被用来构造“同值函
数”的是( )
A. B. C. D.
第1页/共6页
学科网(北京)股份有限公司5. 设函数 在区间 上单调递减,则 取值范围是( )
的
A. B. C. D.
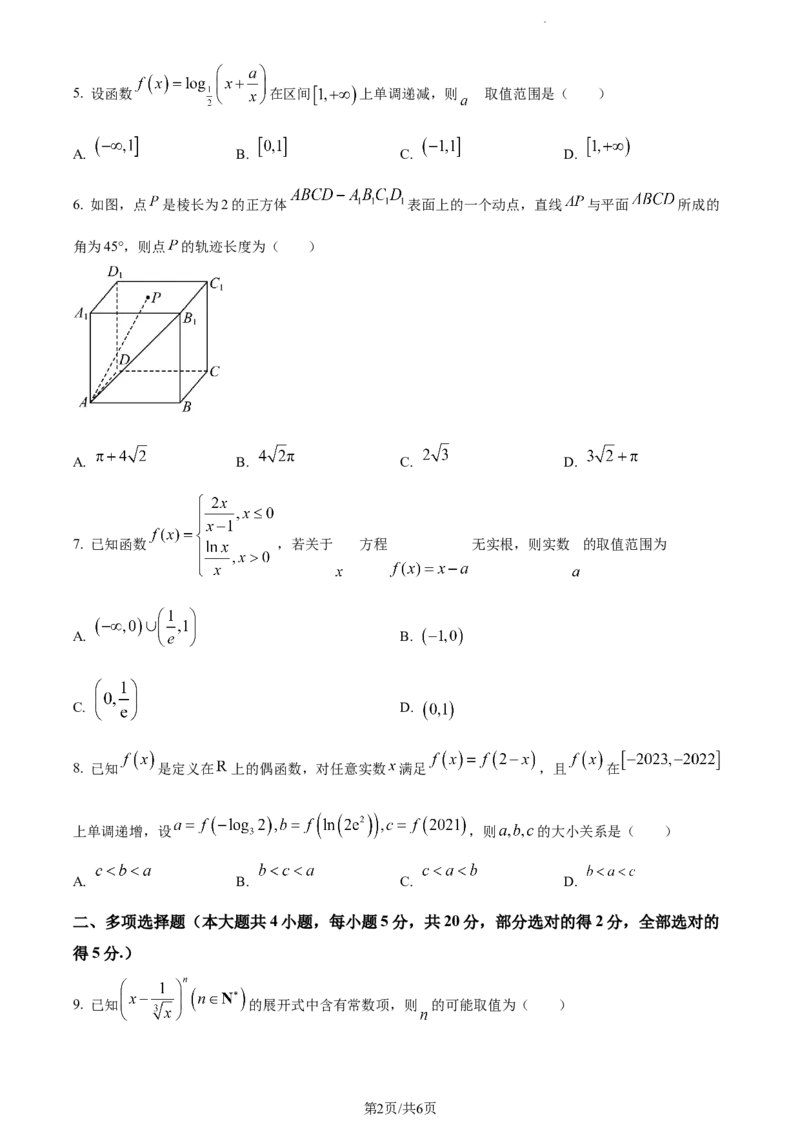
6. 如图,点 是棱长为2的正方体 表面上的一个动点,直线 与平面 所成的
角为45°,则点 的轨迹长度为( )
A. B. C. D.
7. 已知函数 ,若关于 方程 无实根,则实数 的取值范围为
的
A. B.
C. D.
8. 已知 是定义在 上的偶函数,对任意实数 满足 ,且 在
上单调递增,设 ,则 的大小关系是( )
A. B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分,部分选对的得2分,全部选对的
得5分.)
9. 已知 的展开式中含有常数项,则 的可能取值为( )
第2页/共6页
学科网(北京)股份有限公司A. 4 B. 6 C. 8 D. 10
为
10. 小张等四人去甲、乙、丙三个景点旅游,每人只去一个景点,记事件A “恰有两人所去景点相同”,事
件 为“只有小张去甲景点”,则( )
A. 这四人不同的旅游方案共有64种 B. “每个景点都有人去”的方案共有72种
C. D. “四个人只去了两个景点”的概率是
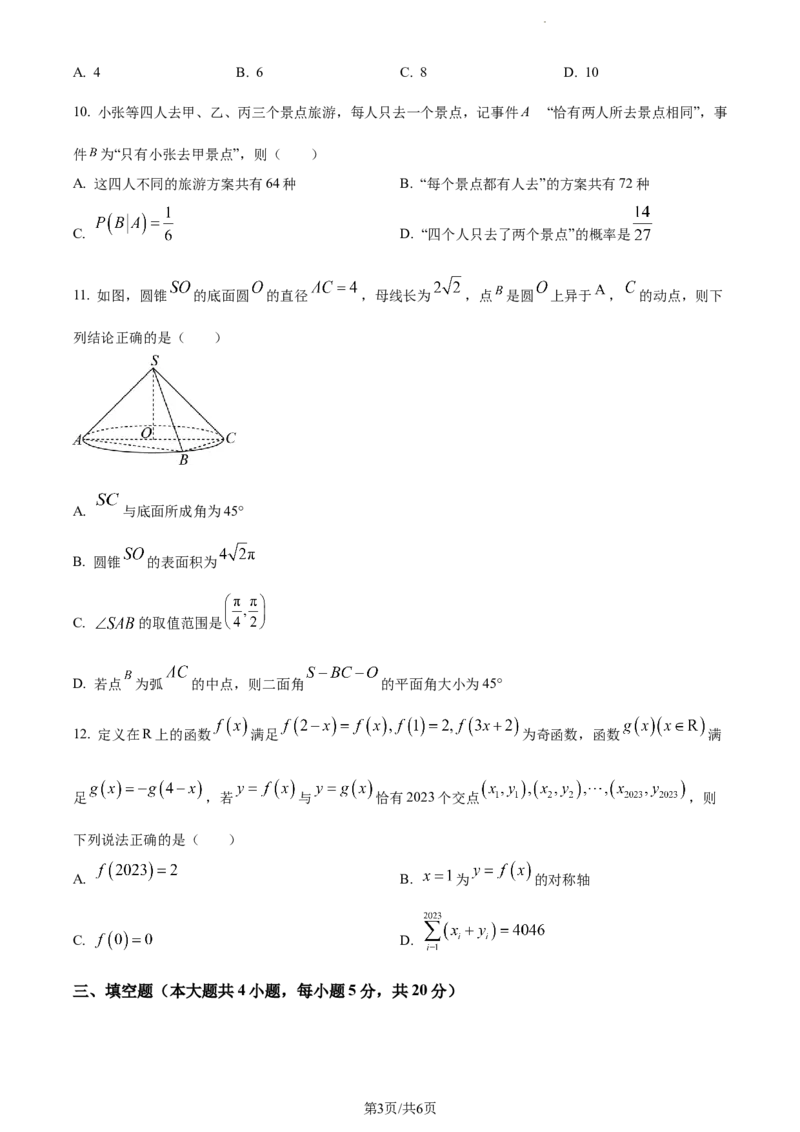
11. 如图,圆锥 的底面圆 的直径 ,母线长为 ,点 是圆 上异于 , 的动点,则下
列结论正确的是( )
A. 与底面所成角为45°
B. 圆锥 的表面积为
C. 的取值范围是
D. 若点 为弧 的中点,则二面角 的平面角大小为45°
12. 定义在R上的函数 满足 为奇函数,函数 满
足 ,若 与 恰有2023个交点 ,则
下列说法正确的是( )
A. B. 为 的对称轴
C. D.
三、填空题(本大题共4小题,每小题5分,共20分)
第3页/共6页
学科网(北京)股份有限公司13. 若 ,则z在复平面内对应的点位于第______象限.
14. 某校期末统考数学成绩服从正态分布 .按 , , , 的比例将考试成绩划
为 四个等级,其中分数大于或等于83分的为 等级,则 等级的分数应为___________.(用
区间表示)
15. 一生产过程有4道工序,每道工序需要安排一人照看.现从甲、乙、丙等7名工人中安排4人分别照
看一道工序,第一道工序只能从甲、乙两工人中安排1人,第四道工序只能从甲、丙两工人中安排1人,
则不同的安排方案共有__________种
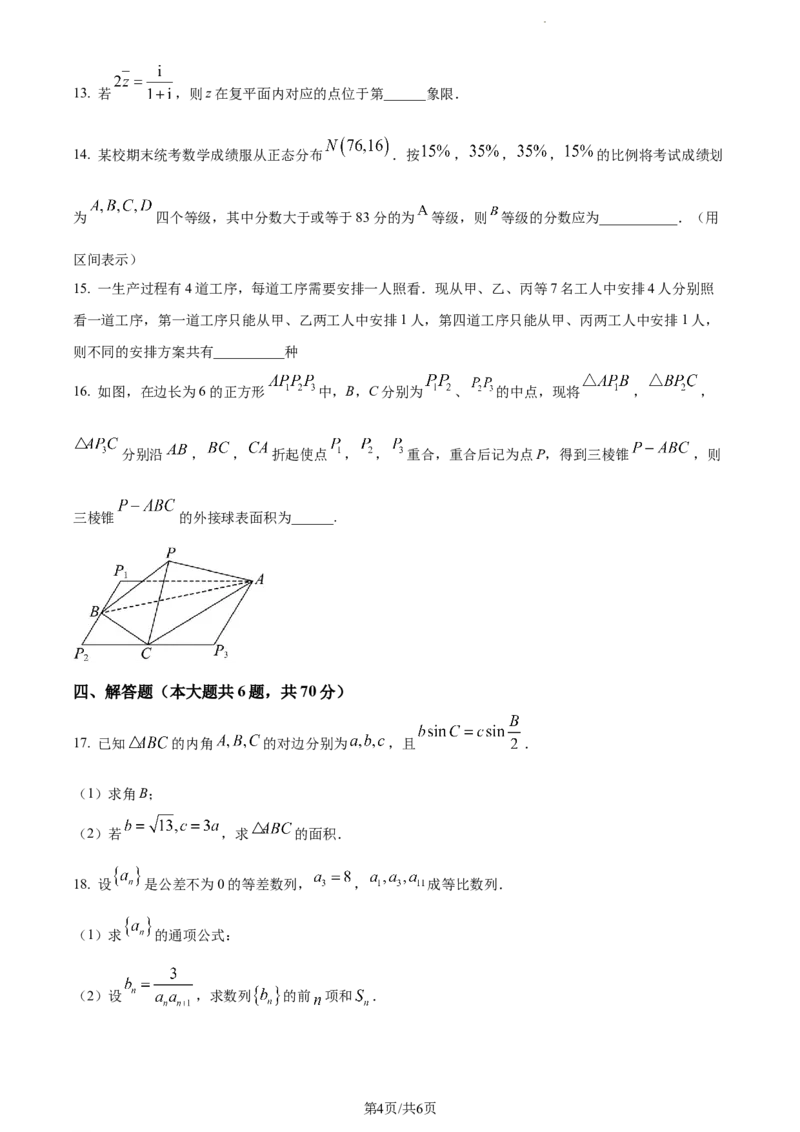
16. 如图,在边长为6的正方形 中,B,C分别为 、 的中点,现将 , ,
分别沿 , , 折起使点 , , 重合,重合后记为点P,得到三棱锥 ,则
三棱锥 的外接球表面积为______.
四、解答题(本大题共6题,共70分)
17. 已知 的内角 的对边分别为 ,且 .
(1)求角B;
(2)若 ,求 的面积.
18. 设 是公差不为0的等差数列, , 成等比数列.
(1)求 的通项公式:
(2)设 ,求数列 的前 项和 .
第4页/共6页
学科网(北京)股份有限公司在
19. 如图, 正三棱柱 中,点 在棱 上,且 .
(1)求证: 平面 ;
(2)若正三棱柱 的底面边长为 ,二面角 的大小为 ,求直线 到平面
的距离.
20. 某闯关游戏必须闯过若干关口才能成功,其中第一关是答题,分别设置“文史常识题”“生活常识题”“影
视艺术常识题”这3道题目,规定有两种答题方案:
方案一:答题3道,至少有2道答对
方案二:在这3道题目中,随机选取2道,这2道都答对.
方案一和方案二中只要完成一个,就能通过第一关,假设甲选择方案一、且答对每一道题的概率是 ,乙
选择方案二,且3道题中只能答对其中两道题.
(1)求甲答对题目数量X的分布列与数学期望;
(2)设甲和乙中通过第一关的人数为 ,求 的分布列;
(3)若丙答对这3道题中每一道题的概率都是 ,且这3道题是否答对相互之间没有影响,
丙选择方案一通过第一关的概率为 ,选择方案二通过第一关的概率为 ,直接比较 与 的大小.
21. 已知椭圆 : 的左焦点为 ,左顶点为 ,离心率为 .
(1)求 的方程;
第5页/共6页
学科网(北京)股份有限公司(2)若过坐标原点 且斜率为 的直线 与E交于A,B两点,直线AF与 的另一个交点为 ,
的面积为 ,求直线 的方程.
22. 已知函数 .
(1)若 ,讨论 的单调性.
(2)已知关于 的方程 恰有 个不同的正实数根 .
(i)求 的取值范围;
(ii)求证: .
第6页/共6页
学科网(北京)股份有限公司