文档内容
长安一中 2021 级高三第三次教学质量检测
数学(文科)试题
时间:120分钟 总分:150分
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
.
1 设全集 ,集合 , ,则 等于( )
A. B. C. D.
2. 已知复数 满足 ,则复数 的虚部为( )
A. B. C. D.
3. 设x,y满足约束条件 ,则z=2x+y的最小值是( )
A. -15 B. -9 C. 1 D. 9
4. 有6名选手参加演讲比赛,观众甲猜测:4号或5号选手得第一名;观众乙猜测:3号选手不可能得第一
名;观众丙猜测:1,2,6号选手中的一位获得第一名;观众丁猜测:4,5,6号选手都不可能获得第一名.
比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )
A. 甲 B. 乙 C. 丙 D. 丁
5. 若 为奇函数,则 的单调递增区间是( )
A. B.
C. D.
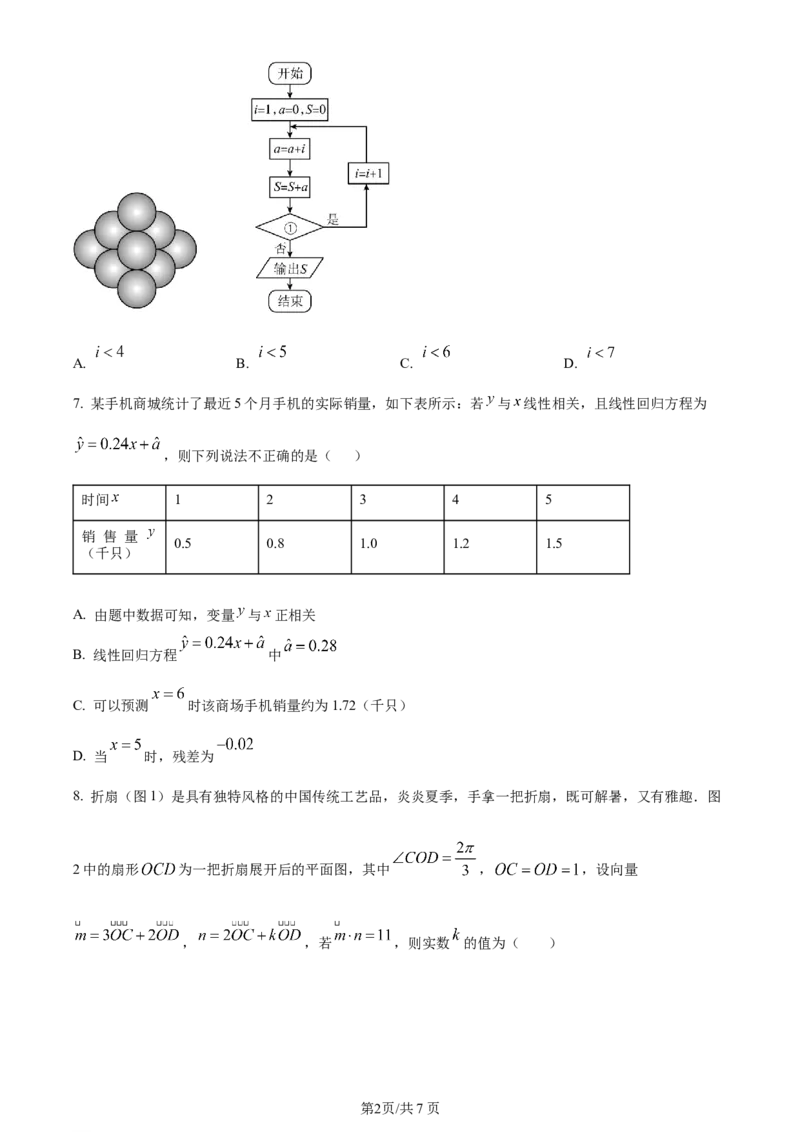
6. 南宋时期的数学家杨辉所著的《详解九章算法》中有一个如图所示的“三角垛”问题,在“三角垛”的最上
层放有一个球,第二层放有3个球,第三层放有6个球,……依此规律,其相应的程序框图如图所示.若
输出的 的值为56,则程序框图中 处可以填入( )
①
第1页/共7页
学科网(北京)股份有限公司A. B. C. D.
7. 某手机商城统计了最近5个月手机的实际销量,如下表所示:若 与 线性相关,且线性回归方程为
,则下列说法不正确的是( )
时间 1 2 3 4 5
销 售 量
0.5 0.8 1.0 1.2 1.5
(千只)
A. 由题中数据可知,变量 与 正相关
B. 线性回归方程 中
C. 可以预测 时该商场手机销量约为1.72(千只)
D. 当 时,残差为
8. 折扇(图1)是具有独特风格的中国传统工艺品,炎炎夏季,手拿一把折扇,既可解暑,又有雅趣.图
2中的扇形 为一把折扇展开后的平面图,其中 , ,设向量
, ,若 ,则实数 的值为( )
第2页/共7页
学科网(北京)股份有限公司A. 1 B. 3 C. 7 D. 14
9. 已知双曲线 的离心率大于 ,则实数 的取值范围是( )
A. B. C. D.
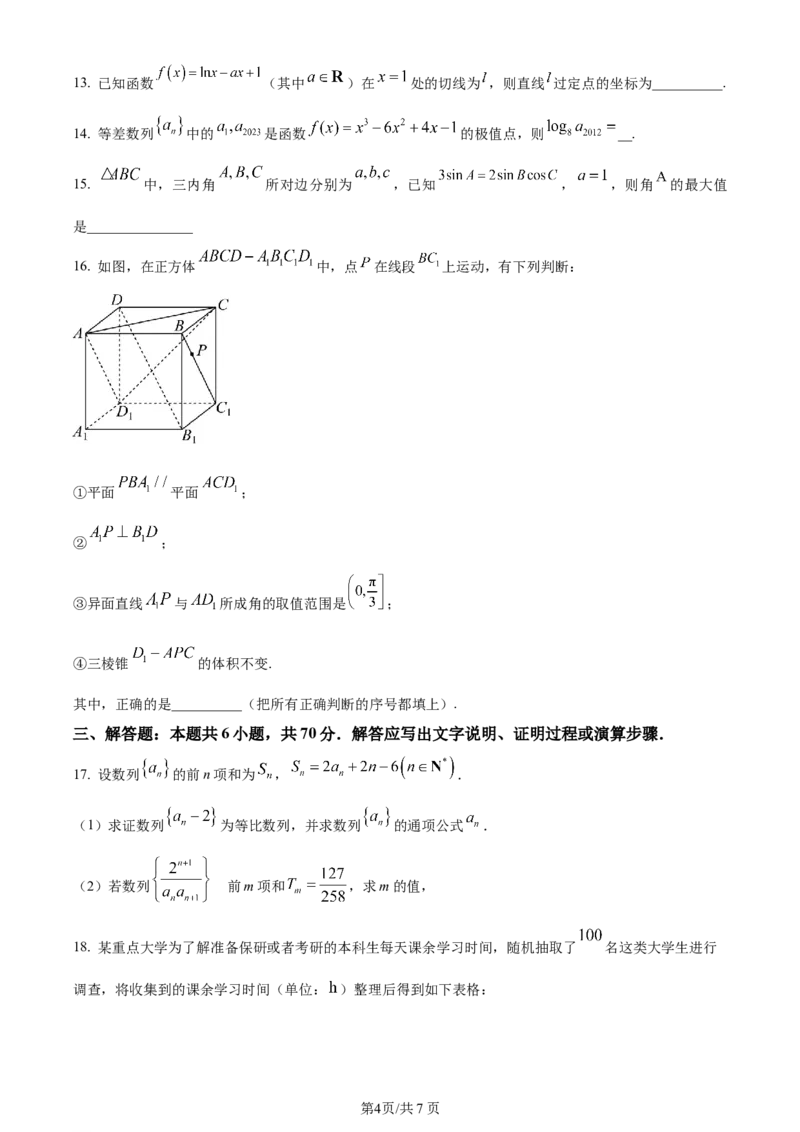
10. 如图,在三棱锥 中, , ,平面 平面ABC,则
三棱锥 外接球的表面积为( )
A. B. C. D.
11. 已知角 , 终边上有一点 ,则 ( )
.
A 2 B. C. D.
12. 过抛物线 的焦点F作直线交C于A,B,过A和原点的直线交 于D,则 面
积的最小值为( )
A. B. 2 C. D.
二、填空题:本题共4小题,每小题5分,共20分.
第3页/共7页
学科网(北京)股份有限公司13. 已知函数 (其中 )在 处的切线为 ,则直线 过定点的坐标为__________.
14. 等差数列 中的 是函数 的极值点,则 __.
15. 中,三内角 所对边分别为 ,已知 , ,则角 的最大值
是_______________
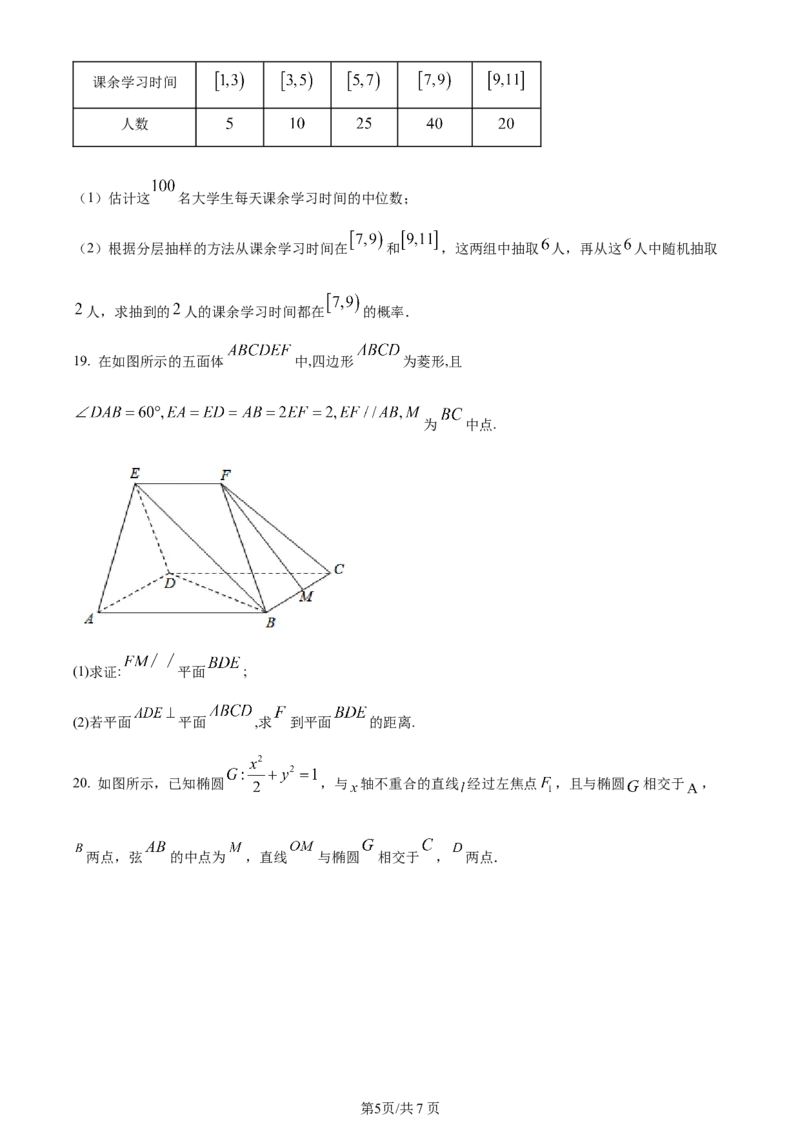
16. 如图,在正方体 中,点 在线段 上运动,有下列判断:
①平面 平面 ;
② ;
③异面直线 与 所成角的取值范围是 ;
④三棱锥 的体积不变.
其中,正确的是__________(把所有正确判断的序号都填上).
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设数列 的前n项和为 , .
(1)求证数列 为等比数列,并求数列 的通项公式 .
(2)若数列 前m项和 ,求m的值,
的
18. 某重点大学为了解准备保研或者考研的本科生每天课余学习时间,随机抽取了 名这类大学生进行
调查,将收集到的课余学习时间(单位: )整理后得到如下表格:
第4页/共7页
学科网(北京)股份有限公司课余学习时间
人数
(1)估计这 名大学生每天课余学习时间的中位数;
(2)根据分层抽样的方法从课余学习时间在 和 ,这两组中抽取 人,再从这 人中随机抽取
人,求抽到的 人的课余学习时间都在 的概率.
19. 在如图所示的五面体 中,四边形 为菱形,且
为 中点.
(1)求证: 平面 ;
(2)若平面 平面 ,求 到平面 的距离.
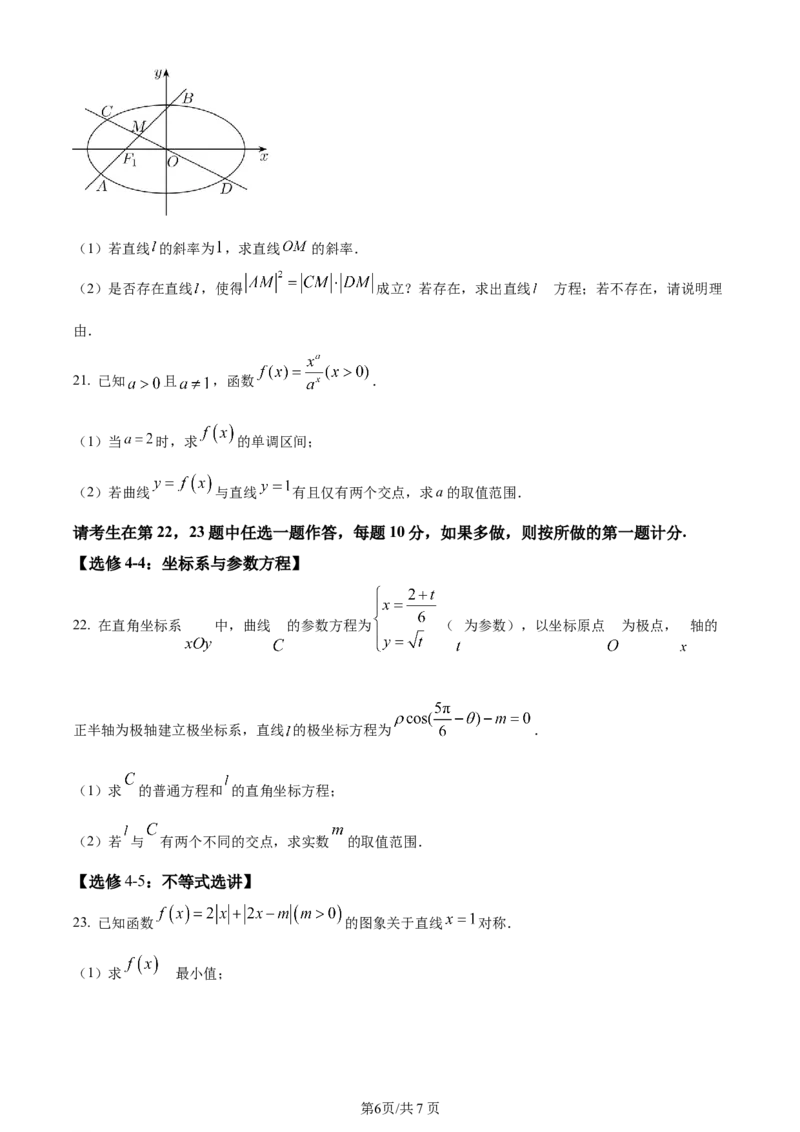
20. 如图所示,已知椭圆 ,与 轴不重合的直线 经过左焦点 ,且与椭圆 相交于 ,
两点,弦 的中点为 ,直线 与椭圆 相交于 , 两点.
第5页/共7页
学科网(北京)股份有限公司(1)若直线 的斜率为 ,求直线 的斜率.
(2)是否存在直线 ,使得 成立?若存在,求出直线 的方程;若不存在,请说明理
由.
21. 已知 且 ,函数 .
(1)当 时,求 的单调区间;
(2)若曲线 与直线 有且仅有两个交点,求a的取值范围.
请考生在第22,23题中任选一题作答,每题10分,如果多做,则按所做的第一题计分.
【选修4-4:坐标系与参数方程】
22. 在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点 为极点, 轴的
正半轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)求 的普通方程和 的直角坐标方程;
(2)若 与 有两个不同的交点,求实数 的取值范围.
【选修4-5:不等式选讲】
23. 已知函数 的图象关于直线 对称.
的
(1)求 最小值;
第6页/共7页
学科网(北京)股份有限公司(2)设 , 均为正数,且 ,求 的最小值.
第7页/共7页
学科网(北京)股份有限公司