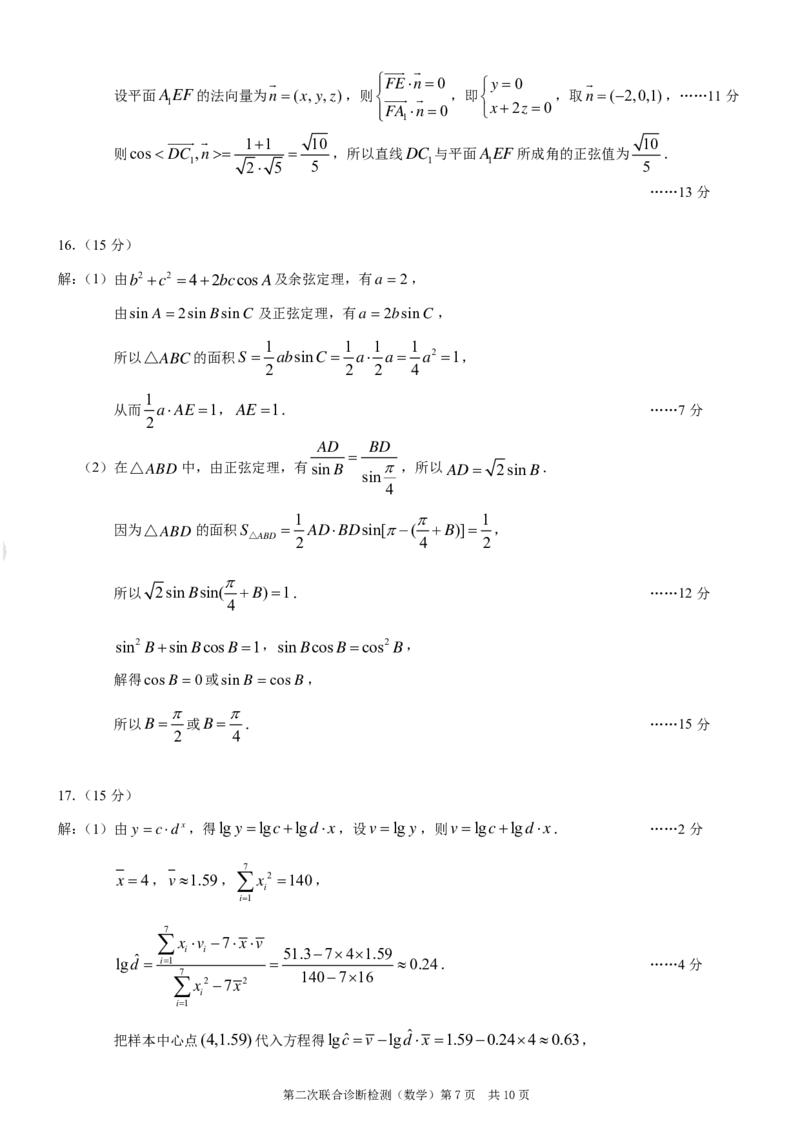重庆康德卷2024二诊数学答案_2024年4月_01按日期_14号_2024届重庆二诊康德卷高三第二次联合诊断检_重庆市2024届高三下学期第二次联考诊断检测数学

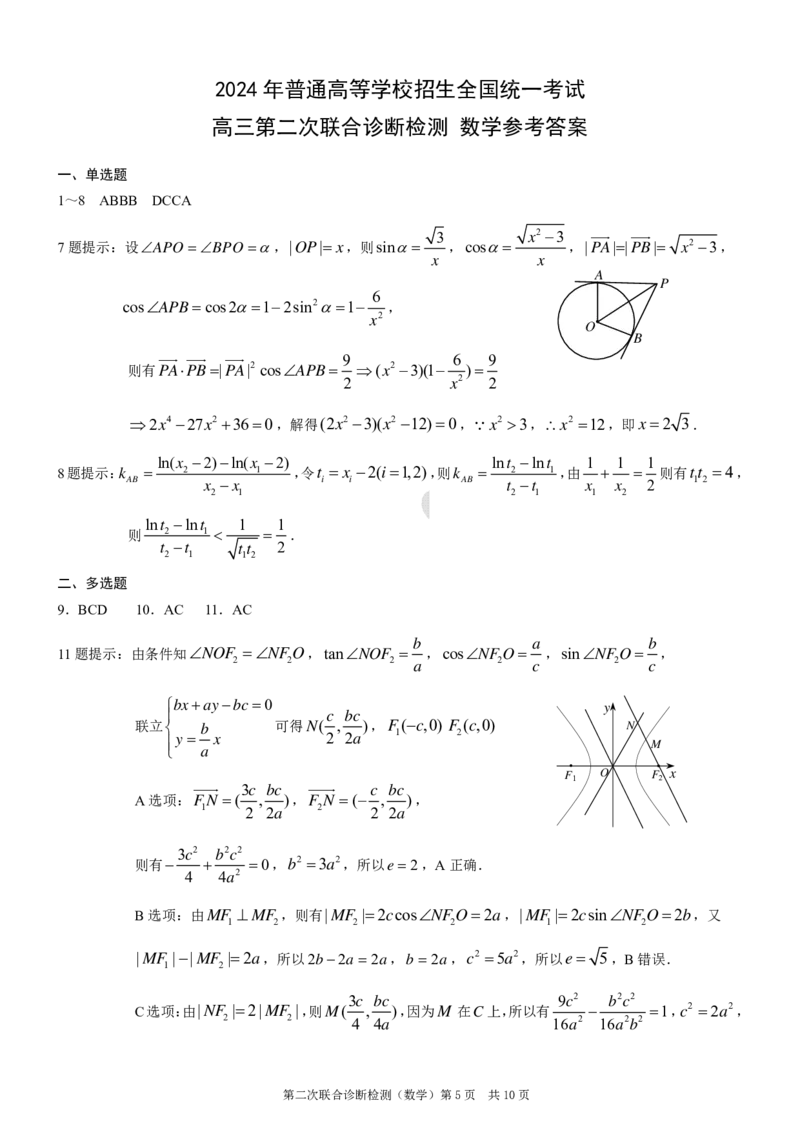
2024 年普通高等学校招生全国统一考试 高三第二次联合诊断检测 数学参考答案 一、单选题 1～8 ABBB DCCA 3 x2 3   7题提示：设APO BPO ，|OP| x，则sin ，cos ，|PA||PB| x2 3， x x A P 6 cosAPBcos212sin21 ， x2 O B    9 6 9 则有PAPB|PA|2 cosAPB (x2 3)(1 ) 2 x2 2 2x4 27x2 360，解得(2x2 3)(x2 12)0，x2 3，x2 12，即x2 3． ln(x 2)ln(x 2) lnt lnt 1 1 1 8题提示：k  2 1 ，令t x 2(i1,2)，则k  2 1 ，由   则有tt 4， AB x x i i AB t t x x 2 1 2 2 1 2 1 1 2 lnt lnt 1 1 则 2 1   ． t t tt 2 2 1 1 2 二、多选题 9．BCD 10．AC 11．AC b a b 11题提示：由条件知NOF NFO，tanNOF  ，cosNFO ，sinNFO ， 2 2 2 a 2 c 2 c bxaybc0 y  c bc 联立 b 可得N( , )，F(c,0) F (c,0) N y  x 2 2a 1 2  M  a F O F x   1 2 3c bc c bc A选项：FN ( , )，F N ( , )， 1 2 2a 2 2 2a 3c2 b2c2 则有  0，b2 3a2，所以e 2，A正确． 4 4a2 B选项：由MF MF ，则有|MF |2ccosNFO2a，|MF |2csinNFO2b，又 1 2 2 2 1 2 |MF ||MF |2a，所以2b2a  2a，b  2a，c2 5a2，所以e 5，B错误． 1 2 3c bc 9c2 b2c2 C选项：由|NF |2|MF |，则M( , )，因为M 在C上，所以有  1，c2 2a2， 2 2 4 4a 16a2 16a2b2 第二次联合诊断检测（数学）第5页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}所以e 2，C正确． 4c2|MF |2 |MF |2 c2 a2 D选项：由|MF ||MF |2a，cosNFO 2 1 ，解得|MF | ， 1 2 2 2|MF |2c 2 2a 2 3a2 c2 3a2 c2 c2 a2 |MF | ，由|MF |5|MF |，即 5 ，解得2a2 c2，所以1e 2， 1 2a 1 2 2a 2a D错误． 三、填空题 27 2 155 12．94% 13． 14．51 （或 ） 14 3 3 n(n1) 128 128 2(x364) 14题提示：易求得a n，S  ．令 f(x) x2  ，x  0，则 f(x)2x  ．当 n n 2 x x2 x2 x(0，4)时，f(x)0，当x(4，)时，f(x)0，所以 f(x)在(0，4)上单调递减，在(4，) 128 128 155 128 64 172 128 2 上单调递增．S2  9  ，S2  36  ，所以S2  的最小值为51 2 S 3 3 3 S 3 3 n S 3 2 3 n 155 (即 )． 3 四、解答题 15．（13分） 解：（1）在△ABD 中，E,F分别为AB,AD的中点，所以EF//BD， 因为EF 平面C BD，BD平面C BD，所以EF //平面C BD． ……2分 1 1 1 1 因为DC//AB，DC  AB EB， 2 由题意DC //DC，DC DC， 1 1 1 1 所以EB//DC 且EBDC ，四边形BCDE为平行四边形， 1 1 1 1 1 1 故DE//CB， 1 1 因为DE平面C BD，C B平面C BD，所以DE//平面C BD． ……5分 1 1 1 1 1 1 因为EF,DE为平面DEF中两相交直线，所以平面DEF//平面C BD． ……6分 1 1 1 1 （2）在△ABD中，AD1，AB  2DC  2，DAB60， z 所以BD 3，ADBD，则AD,DB,DD 两两垂直，……8分 D C 1 1 1  以DA方向为x轴正方向，建立空间直角坐标系Dxyz，如图． A 1 B 1 1 3 1 1 3 D C 则E( , ,0)，F( ,0,0)，A(1,0,1)，C ( , ,1)， F 2 2 2 1 1 2 2 A B  3  1  1 3 E FE (0, ,0)，FA ( ,0,1)，DC ( , ,1)， x y 2 1 2 1 2 2 第二次联合诊断检测（数学）第6页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}    FEn0 y 0  设平面AEF的法向量为n(x,y,z)，则  ，即 ，取n(2,0,1)，……11分 1  FA n0 x2z 0 1   11 10 10 则cos DC ,n  ，所以直线DC 与平面AEF所成角的正弦值为 ． 1 2 5 5 1 1 5 ……13分 16．（15分） 解：（1）由b2 c2 42bccosA及余弦定理，有a  2， 由sin A2sinBsinC 及正弦定理，有a  2bsinC ， 1 1 1 1 所以△ABC的面积S  absinC  a a a2 1， 2 2 2 4 1 从而 aAE 1，AE 1． ……7分 2 AD BD  （2）在△ABD 中，由正弦定理，有sinB ，所以AD 2sinB． sin 4 1  1 因为△ABD 的面积S  ADBDsin[( B)] ， △ABD 2 4 2  所以 2sinBsin( B)1． ……12分 4 sin2 BsinBcosB1，sinBcosBcos2 B， 解得cosB 0或sinB cosB，   所以B 或B ． ……15分 2 4 17．（15分） 解：（1）由y cdx，得lgylgclgdx，设vlgy，则vlgclgdx． ……2分 7 x4，v1.59，x2 140， i i1 7 x v 7xv i i 51.3741.59 lgd ˆ  i1  0.24． ……4分 7 140716 x2 7x2 i i1 ˆ 把样本中心点(4,1.59)代入方程得lgcˆv lgdx 1.590.2440.63， 第二次联合诊断检测（数学）第7页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}所以vˆ0.24x0.63，即lgyˆ 0.24x0.63，其回归方程为yˆ 100.24x0.63=100.63100.24x，……6分 当x 8时， yˆ 100.63100.248 4.2783.18355人． ……8分 （2）X 的可能取值为：0.7a， 0.8a， 0.9a，a． 3 1 3 3 1 P(X 0.7a)  =0.1，P(X 0.8a) +  =0.35， 10 3 10 10 6 3 1 4 P(X 0.9a)  =0.15，P(X a) =0.4， 10 2 10 分布列如下： X 0.7a 0.8a 0.9a a P 0.1 0.35 0.15 0.4 ……13分 所以，购物的平均费用为：E(X)0.7a0.10.8a0.350.9a0.15a0.40.885a． ……15分 18．（17分） x 2 y 2 y 2 b2 解：（1）A(a,0),B(a,0)，设P(x ,y )，有 0  0 1 0  ， 0 0 a2 b2 x 2 a2 a2 0 y y 3 b2 3 3 又 0  0  ，  ， a2 b2 a2 c2． x a x a 4 a2 4 4 0 0 由题意，|PF ||PF ||FF |6，2a2c 6，即ac 3，解得a2，b2 3． 1 2 1 2 x2 y2 所以椭圆C 的方程为  1． ……5分 4 3 x2 y2   1 （2）设直线l:xty1，联立 4 3 ，得(3t2 4)y2 6ty90，  xty1 1 5 t 设D(x,y )，E(x ,y )，则|FD| (x 1)2  y2 2 x   y ， 1 1 2 2 1 1 1 2 1 2 2 1 5 t 2 |FE|  y ，|DE| 1t2 | y  y |．点F 到直线l的距离为d  ． ……8分 1 2 2 2 1 2 1 1t2 1 1 △DEF 面积S  |DE|d  |FD||FE|sinDFE． 1 △DEF 1 2 2 1 1 1 设△DEF 外接圆半径为R， 1 第二次联合诊断检测（数学）第8页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}|DE| |DE||FD||FE| 1t2 |FD||FE| 由正弦定理，有2R  1 1  1 1 sinDFE |DE|d 2 1 1t2 5 t 5 t 1t2(9t2 25)  (  y )(  y ) ． ……12分 2 2 2 1 2 2 2 2(3t2 4) 9m316m 令 1t2 m，m1，则4R ． 3m2 1 9x316x 27x4 21x2 16 令 y  ，则y ， 3x2 1 (3x2 1)2 因为212 416270， 27x4 21x2 16 9x316x 所以y 0，y  在[1,)上单调递增， (3x2 1)2 3x2 1 从而当m 1，即t 0时，R取最小值，即△DEF 外接圆面积最小， 1 此时直线l的方程为：x1． ……17分 19．（17分） x ln(2x) 2x 解：（1） f(x)的定义域为(,1)(1,2)， f(x) ， [ln(2x)]2 x 1 2xx x 令(x)ln(2x) ，则(x)   ． 2x 2x (2x)2 (2x)2 当x  0时，(x)0；当x(0,1)(1,2)时，(x)0． 所以(x)(0)ln20，从而 f(x)0， 故 f(x)在(,1)单调递增，在(1,2)上单调递增． f(x)的单调递增区间为(,1)，(1,2)． ……4分 a x ax （2）当0 x 1时，由 f(x) a，得  ，即x1aln(2x)． x1 ln(2x) x1 a 2ax 令g(x) x1aln(2x)，0 x 1，则g(x)1  ， 2x 2x ①若2a0，即a2，g(x)0，g(x)在(0,1)单调递减，所以g(x)0，不合题意； ②若2a 1，即a1，g(x)0，g(x)在(0,1)单调递增，所以g(x)0，符合题意； ③若0 2a 1，即2 a  1，当x(0,2a)时，g(x)0，g(x)单调递增，当x(2a,1)， 第二次联合诊断检测（数学）第9页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}g(x)0，g(x)单调递减，所以g(2a)1aaln(a)0，不合题意． 综上a1． ……9分 a a （3）由题意，a  n1 ，若0a 1，则0 n1 1， n ln(2a ) n ln(2a ) n1 n1 a 1 1 f(0) n1  f( )，由（1）知， f(x)在(,1)上单调递增，所以0a  1， ln(2a ) 2 n1 2 n1 1 综上，若0a 1，则0a 1．因为a  (0,1)，所以0a 1，nN．……11分 n n1 1 3 n 由（2）知，当0 x1时，ln(2x)1x（取a 1时）， 1 1 所以a a ln(2a )a (1a )，有  1．……（★） n1 n n1 n n1 a a n1 n 1 1 1 所以  (n1)n2(n2)，a  (n2) a a n n2 n 1 1 1 又a  ，故a  ． ……13分 1 3 n n2 5 1 由（★）知，{a }单调递减，所以ln(2a )ln(2a )ln(2a )ln  ， n n1 n 1 3 2 1 1 1 从而a a ln(2a ) a ，故a   ． ……17分 n1 n n1 2 n n 3 2n1 第二次联合诊断检测（数学）第10页 共10页 {#{QQABIQIEogiAAJIAARgCEQVQCAGQkBACACoGgEAIsAABiANABAA=}#}