广西部分示范性高中2025届高三上学期摸底质检数学试题+答案(1)_2024-2025高三（6-6月题库）_2024年09月试卷_0912广西2025届金太阳高三9月联考（24-25C）

高三数学考试 注意事项： 1.答题前，考生务必将自已的姓名､考生号､考场号､座位号填写在答题卡上 2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改 动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上.写在本 试卷上无效. 3.考试结束后，将本试卷和答题卡一并交回. 4.本试卷主要考试内容：高考全部内容. 一､选择题：本题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有一项是 符合题目要求的. 1.若集合M = { x∣x2 −4x−50 } ,N ={ x∣−4x2 } ，则M ∪N =（ ） A. [−4,5 ] B. [−1,3 ] C. [−4,2 ] D. [−1,2 ] 2z−1 2.若 =1+i，则z =（ ） z 1 1 1 1 A.− − i B.− + i 2 2 2 2 1 1 1 1 C. + i D. − i 2 2 2 2 3.2024年1月至5月重庆市八大类商品和服务价格增长速度依次为3.1%,2.5%,1.9%， 1.0%,0.8%,0.5%,−0.1%,−2.6%，则该组数据的第75百分位数为（ ） A.1.0% B.2.2% C.1.9% D.2.5% 4.甲同学每次投篮命中的概率为 p，在投篮6次的实验中，命中次数X 的均值为2.4，则X 的方差为 （ ） A.1.24 B.1.44 C.1.2 D.0.96 5.已知函数 f ( x )=ax −2(a>0，且a≠1)的图象不经过第一象限，则函数 g ( x )=log 1 ( x+2 ) 的图象不 a 经过（ ） A.第一象限 B.第二象限 C.第三象限 D.第四象限 x2 y2 6.已知椭圆M : + =1(a>b>0)的左､右焦点分别为F,F ，点P在M 上，Q为PF 的中点，且 a2 b2 1 2 2 FQ⊥ PF , FQ =b，则M 的离心率为（ ） 1 2 1 3 1 1 2 A. B. C. D. 3 3 2 2 学科网（北京）股份有限公司7.已知正四面体的高等于球O的直径，则正四面体的体积与球O的体积之比为（ ） 3 3 3 2 3 2 3 3 A. B. C. D. 4π 2π 4π 2π 8.在ABC中，sin ( A−C )+sinC =sinB，且BC边上的高为 3 ，则（ ） 2 3 A.ABC的面积有最大值，且最大值为 2 3 B.ABC的面积有最大值，且最大值为 4 3 C.ABC的面积有最小值，且最小值为 2 3 D.ABC的面积有最小值，且最小值为 4 二､多选题：本题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项符合题目 要求.全部选对的得 6分，部分选对的得部分分，有选错的得 0分. 9.已知点 ( 1,2 ) 到抛物线C:x2 =my准线的距离为4，则m的值可能为（ ） A.8 B.−8 C.24 D.−24  π 1 10.将函数 f ( x )=2sinx+ 图象的横坐标缩短为原来的 ，纵坐标不变，得到函数g ( x ) 的图象，则  6 2 （ ）  π A. f x+ 为偶函数  3 ( ) B.g x 的最小正周期为4π π 2π ( ) ( ) C. f x 与g x 在 , 上均单调递减 3 3  D.函数y = f ( x )−g ( x ) 在 [ 0,2π ] 上有5个零点 11.若函数 f ( x )= x3+ax2 +bx+c，则（ ） ( ) A. f x 可能只有1个极值点 ( ) B.当 f x 有极值点时，a2 >3b 学科网（北京）股份有限公司C.存在a，使得点 ( 0, f ( 0 )) 为曲线y = f ( x ) 的对称中心 4 D.当不等式 f ( x )<0的解集为 (−∞,1 )∪( 1,2 ) 时， f ( x ) 的极小值为− 27 三､填空题：本题共 3小题，每小题 5分，共 15分.     12.若向量a =(−2,3 ) ,b =( m+1,2 )，且a∥ b ，则m=__________. 13.已知 { a +3 } 是等比数列，a =−2,a =−1，则数列 { a } 的前n项和为__________. n 1 2 n 14.甲､乙玩一个游戏，游戏规则如下：一个盒子中装有标号为1,2,3,4,5,6的6个大小质地完全相同的小 球，甲先从盒子中不放回地随机取一个球，乙紧接着从盒子中不放回地随机取一个球，比较小球上的数 字，数字更大者得1分，数字更小者得0分，以此规律，直至小球全部取完，总分更多者获胜.甲获得3分 的概率为__________. 四､解答题：本题共 5小题，共 77分.解答应写出文字说明､证明过程或演算步骤. 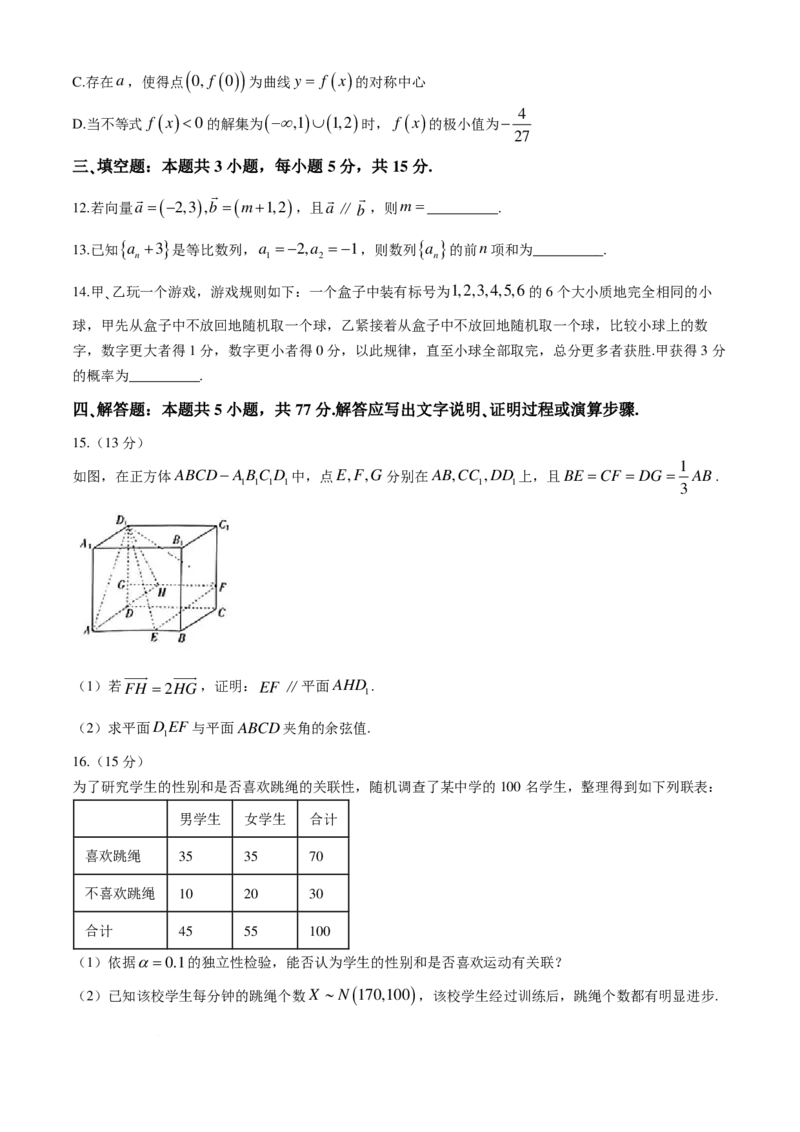15.（13分） 1 如图，在正方体ABCD−ABC D 中，点E,F,G分别在AB,CC ,DD 上，且BE =CF = DG = AB. 1 1 1 1 1 1 3   （1）若FH =2HG，证明：EF ∥平面AHD . 1 （2）求平面DEF与平面ABCD夹角的余弦值. 1 16.（15分） 为了研究学生的性别和是否喜欢跳绳的关联性，随机调查了某中学的100名学生，整理得到如下列联表： 男学生 女学生 合计 喜欢跳绳 35 35 70 不喜欢跳绳 10 20 30 合计 45 55 100 （1）依据α=0.1的独立性检验，能否认为学生的性别和是否喜欢运动有关联？ （2）已知该校学生每分钟的跳绳个数X ∼ N ( 170,100 ) ，该校学生经过训练后，跳绳个数都有明显进步. 学科网（北京）股份有限公司假设经过训练后每人每分钟的跳绳个数都增加10，该校有1000名学生，预估经过训练后该校每分钟的跳 [ ] 绳个数在 170,200 内的人数（结果精确到整数）. n(ad −bc)2 附：χ2 = ，其中n=a+b+c+d . ( a+b )( c+d )( a+c )( b+d ) α 0.1 0.05 0.01 x 2.706 3.841 6.635 α 若X ∼ N ( µ,σ2 ) ，则P (µ−σ X µ+σ)≈0.6827,P (µ−2σ X µ+2σ)≈0.9545， P (µ−3σ X µ+3σ)≈0.9973. 17（15分） 已知函数 f ( x )=e2x −( a+b ) x+2，且曲线y = f ( x ) 在点 ( 0, f ( 0 )) 处的切线斜率为2−2a. （1）比较a和b的大小； ( ) （2）讨论 f x 的单调性； ( ) ( ) ( ) （3）若 f x 有最小值，且最小值为g a ，求g a 的最大值. 18.（17分） 已知平面内一动点P到点F (−2,0 ) 的距离与点P到定直线x=− 3 的距离之比为 2 3 ，记动点P的轨迹 2 3 为曲线C. （1）求曲线C的方程. 3 （2）在直线y = x上有一点M ，过点M 的直线l与曲线C相交于A,B两点.设 3 ( ) l:x=my−n m2 >3 ，证明： MA MB 只与m有关. 19.（17分） 若数列 { a } 满足a2 +a a a +a ，且a >0，则称数列 { a } 为“稳定数列”. n n+1 n n+2 n n+2 n n （1）若数列m,m,2为“稳定数列”，求m的取值范围； （2）若数列 { b } 的前n项和S = 1( n2 +n ) ，判断数列 { b } 是否为“稳定数列”，并说明理由； n n 8 n （3）若无穷数列 { c } 为“稳定数列”，且 { c } 的前n项和为T ，证明：当n2时，T +2T +n. n n n n 2 学科网（北京）股份有限公司高三数学考试参考答案 1.A 由题意得M =[−1,5 ] ，所以M ∪N =[−4,5 ] . 1 1 1+i 1 1 2.C 由题意得2− =1+i，则z = = = + i . z 1−i ( 1−i )( 1+i ) 2 2 1.9%+2.5% 3.B 因为8×75%=6，所以该组数据的第75百分位数为 =2.2%. 2 4.B 由题意得E ( X )=6p=2.4，则 p=0.4，所以D ( X )=6p ( 1− p )=1.44. 5.D 当a>1时， f ( x )=ax −2的图象经过第一､三､四象限，不经过第二象限， 当01，所以 1 的图象经过第一､二､三象限，不经过第四象限. a a 1 1 6.C 由题意得 PF = FF =2c，则 QF = PF = ( 2a− PF ) =a−c.在QFF 中，由 1 1 2 2 2 2 2 1 1 2 FQ 2 + QF 2 = FF 2，得b2 +(a−c)2 =4c2，则a2 −c2 +a2 −2ac+c2 =4c2，得 1 2 1 2 c 1 a2 −ac−2c2 =( a−2c )( a+c )=0，解得a =2c，所以M 的离心率为 = . a 2 2 2 3  6 7.A 设正四面体的边长为a，球O的半径为R，易得正四面体的高h= a2 − × a = a，则   3 2 3   6 1 1 6 2 R= a.正四面体的体积V = × a2sin60× a= a3，球O的体积 6 1 3 2 3 12 3 4 4  6  6 V 3 3 V = πR3 = π× a = πa3，所以 1 = . 2 3 3  6  27 V 4π   2 8.D 设ABC的内角A,B,C的对边分别为a,b,c.由题意得sin ( A−C )+sinC =sin(A+C），得 sinAcosC−sinCcosA+sinC =sinAcosC+sinCcosA，得2sinCcosA=sinC.因为sinC ≠0，所以  1 1 3 1 π S = bcsinA= a× , a=bc, cosA= ，即A= .由 ABC 2 2 2 得 ，则 2 3  a2 =b2 +c2 −bc, a2 =b2 +c2 −2bccosA, b2c2 =b2 +c2 −bc2bc−bc，得bc1（当且仅当b=c=1时，等号成立），所以 3 3 3 S ABC = 4 bc 4 ，则S ABC 有最小值，且最小值为 4 . 学科网（北京）股份有限公司m m 9.AD 由题意得C的准线方程为 y =− ，则 − −2 =4，解得m=8或−24. 4 4  π  π 10ACD f x+  =2sinx+  =2cosx为偶函数，A正确.  3  2  π 2π 由题意得g ( x )=2sin2x+ ,g ( x ) 的最小正周期T = =π，B错误. 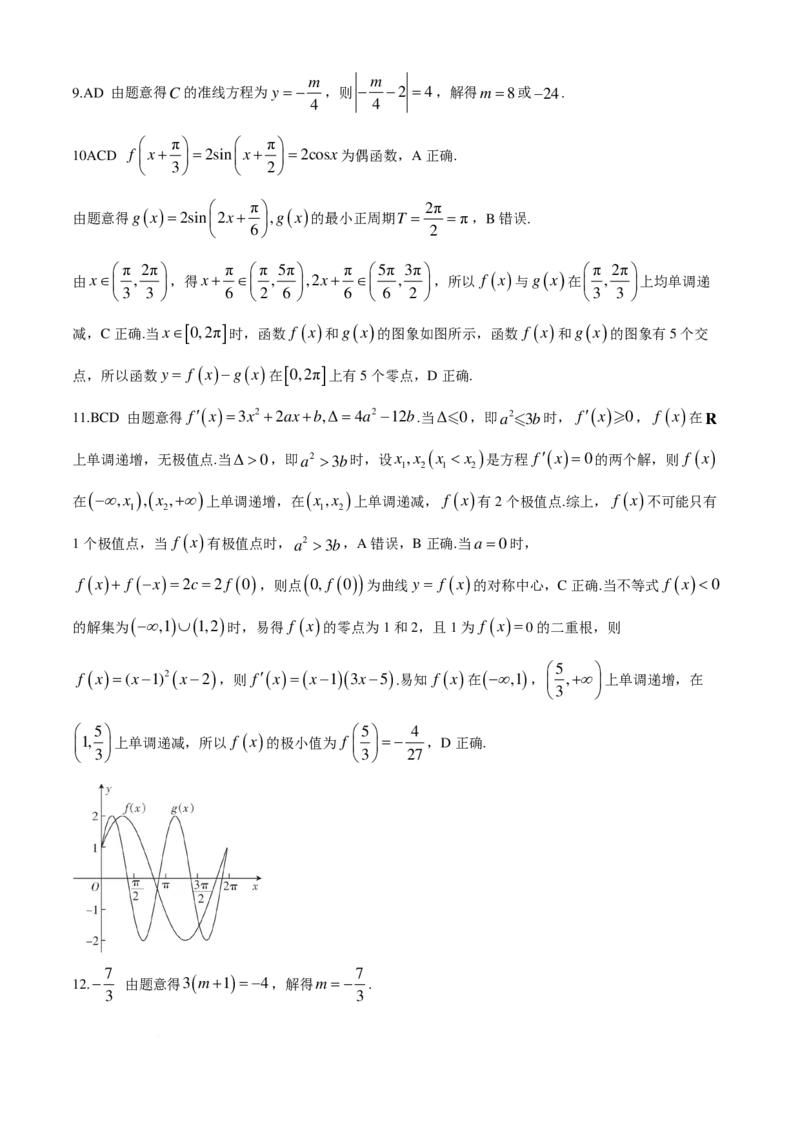 6 2 π 2π π π 5π π 5π 3π π 2π 由x∈  , ，得x+ ∈  , ,2x+ ∈  , ，所以 f ( x ) 与g ( x ) 在 , 上均单调递 3 3  6 2 6  6  6 2  3 3  减，C正确.当x∈[ 0,2π ] 时，函数 f ( x ) 和g ( x ) 的图象如图所示，函数 f ( x ) 和g ( x ) 的图象有5个交 点，所以函数y = f ( x )−g ( x ) 在 [ 0,2π ] 上有5个零点，D正确. 11.BCD 由题意得 f′( x )=3x2 +2ax+b,Δ=4a2 −12b.当Δ0，即a2 3b时， f′( x ) 0， f ( x ) 在R 上单调递增，无极值点.当Δ>0，即a2 >3b时，设x ,x ( x < x ) 是方程 f′( x )=0的两个解，则 f ( x ) 1 2 1 2 在 (−∞,x ) , ( x ,+∞) 上单调递增，在 ( x ,x ) 上单调递减， f ( x ) 有2个极值点.综上， f ( x ) 不可能只有 1 2 1 2 ( ) 1个极值点，当 f x 有极值点时，a2 >3b，A错误，B正确.当a =0时， f ( x )+ f (−x )=2c=2f ( 0 ) ，则点 ( 0, f ( 0 )) 为曲线y = f ( x ) 的对称中心，C正确.当不等式 f ( x )<0 的解集为 (−∞,1 )∪( 1,2 ) 时，易得 f ( x ) 的零点为1和2，且1为 f ( x )=0的二重根，则 5  f ( x )=(x−1)2( x−2 ) ，则 f′( x )=( x−1 )( 3x−5 ) .易知 f ( x ) 在 (−∞,1 ) ， ,+∞ 上单调递增，在 3   5 5 4 1, 上单调递减，所以 f ( x ) 的极小值为 f   =− ，D正确.  3 3 27 7 7 12.− 由题意得3 ( m+1 )=−4，解得m=− . 3 3 学科网（北京）股份有限公司a +3 13.2n −3n−1 设等比数列 { a +3 } 的公比为q，则q= 2 =2，得a +3=( a +3 )⋅2n−1， n a +3 n 1 1 则a =2n−1−3，所以 { a } 的前n项和为20 −3+2−3+22 −3++2n−1−3= 2n −1 −3n=2n −3n−1 n n 2−1 1 14. 若甲获得3分，则甲必取中6号球，乙必取中1号球. 8 A3A3 1 当甲小球上的数字为6,5,4时，甲获得3分的概率为 3 3 = ； A6 20 6 2×2×A3 1 当甲小球上的数字为6,5,3时，甲获得3分的概率为 3 = ； A6 30 6 2A3 1 当甲小球上的数字为6,5,2时，甲获得3分的概率为 3 = ； A6 60 6 2A3 1 当甲小球上的数字为6,4,3时，甲获得3分的概率为 3 = ； A6 60 6 A3 1 当甲小球上的数字为6,4,2时，甲获得3分的概率为 3 = . A6 120 6 1 1 1 1 1 综上，甲获得3分的概率为 + +2× + = . 20 30 60 120 8 15.（1）证明：FC =GD且FC∥GD,∴四边形CDGF是平行四边形， ∴CD= FG且CD∥ FG. 2 2 FH = CD，且FH ∥CD,AE = CD，且AE∥CD， 3 3 ∴AE = FH ，且AE∥ FH ， ∴四边形AEFH 是平行四边形，∴EF ∥ AH . 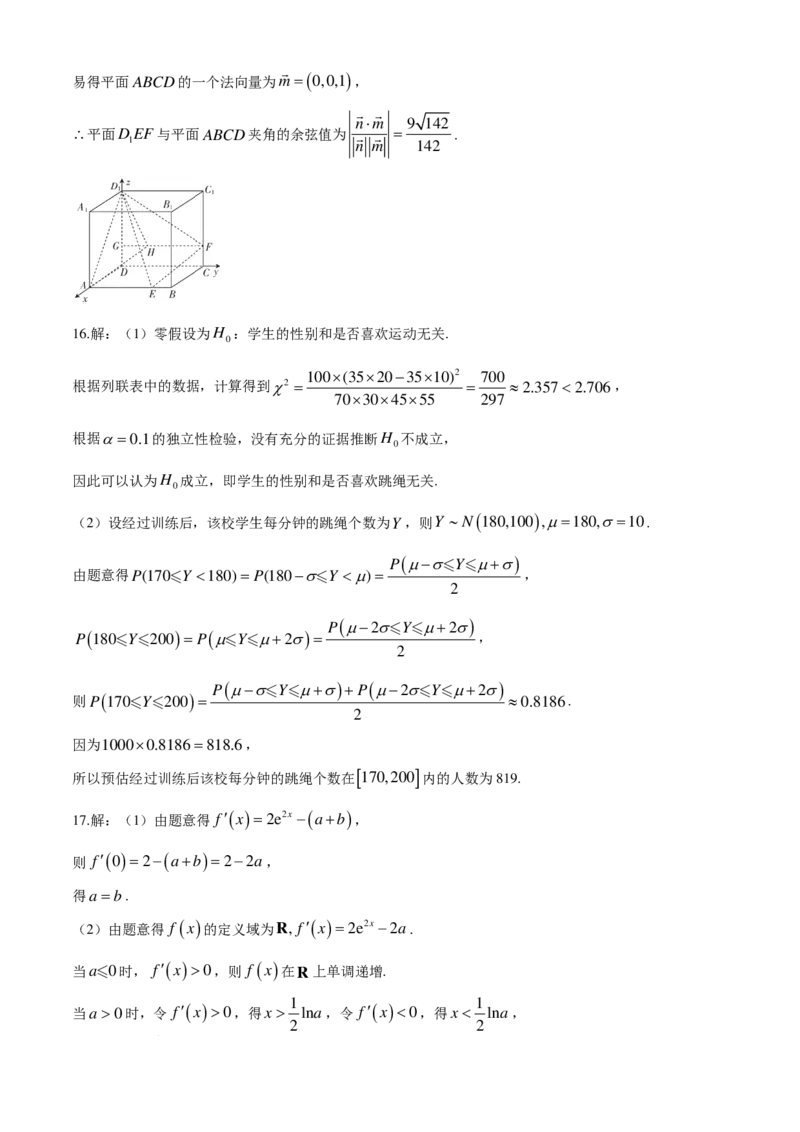EF ⊄平面AHD,AH ⊂平面AHD,∴EF ∥平面AHD 1 1 1 （2）解：以D为原点，DA为3个单位长度，DA,DC,DD 所在直线分别为x轴､ y轴､z轴，建立如图 1 所示的空间直角坐标系，   则D ( 0,0,3 ) ,E ( 3,2,0 ) ,F ( 0,3,1 ) ,DE =( 3,2,−3 ) ,DF =( 0,3,−2 ) . 1 1 1     n⋅DE =3x+2y−3z =0, 设平面DEF的法向量为n =( x,y,z ) ，则 1 ，取x=5，则y =6,z =9，得 1 n⋅DF =3y−2z =0, 1  n =( 5,6,9 ) . 学科网（北京）股份有限公司 易得平面ABCD的一个法向量为m=( 0,0,1 ) ，   n⋅m 9 142 ∴平面DEF与平面ABCD夹角的余弦值为   = . 1 n m 142 16.解：（1）零假设为H ：学生的性别和是否喜欢运动无关. 0 100×(35×20−35×10)2 700 根据列联表中的数据，计算得到χ2 = = ≈2.357<2.706， 70×30×45×55 297 根据α=0.1的独立性检验，没有充分的证据推断H 不成立， 0 因此可以认为H 成立，即学生的性别和是否喜欢跳绳无关. 0 （2）设经过训练后，该校学生每分钟的跳绳个数为Y ，则Y ∼ N ( 180,100 ) ,µ=180,σ=10. P (µ−σ Y µ+σ) 由题意得P(170Y <180)= P(180−σ Y <µ)= ， 2 P ( 180Y200 )= P (µ Y µ+2σ)= P (µ−2σ Y µ+2σ) ， 2 则P ( 170Y200 )= P (µ−σ Y µ+σ)+P (µ−2σ Y µ+2σ) ≈0.8186. 2 因为1000×0.8186=818.6， [ ] 所以预估经过训练后该校每分钟的跳绳个数在 170,200 内的人数为819. 17.解：（1）由题意得 f′( x )=2e2x −( a+b ) ， 则 f′( 0 )=2−( a+b )=2−2a， 得a =b. （2）由题意得 f ( x ) 的定义域为R, f′( x )=2e2x −2a. 当a0时， f′( x )>0，则 f ( x ) 在R上单调递增. 1 1 当a >0时，令 f′( x )>0，得x> lna，令 f′( x )<0，得x< lna， 2 2 学科网（北京）股份有限公司 1  1  则 f ( x ) 在 −∞, lna上单调递减，在 lna,+∞ 上单调递增.  2  2  ( ) （3）由（2）可知当a0时， f x 没有最小值， 1  则a>0,g ( a )= f(x) = f  lna =a−alna+2， min 2  得g′( a )=−lna. 当00,g ( a ) 单调递增， 当a>1时，g′( a )<0,g ( a ) 单调递减， 所以g(a) = g ( 1 )=3. max (x+2)2 + y2 2 3 = ( ) 18.（1）解：设P x,y ，由题意得 3 3 ， x+ 2 x2 化简得曲线C的方程为 − y2 =1. 3 ( ) ( ) （2）证明：设A x ,y ,B x ,y . 1 1 2 2 x=my+n,  ( ) 联立x2 得 m2 −3 y2 +2mny+n2 −3=0，  − y2 =1,  3 ( )( ) ( ) 因为m2 >3，所以m2 −3>0，所以Δ=(2mn)2 −4 m2 −3 n2 −3 =12 m2 +n2 −3 >0,  −2mn y + y =   1 2 m2 −3 则  n2 −3 y y = .  1 2 m2 −3 x=my+n,  n 联立 y = 3 x, 得y 0 = 3−m .  3 MA = ( x −x )2 +( y − y )2 = 1+m2 y − y ， 0 1 0 1 0 1 同理可得 MB = 1+m2 y − y ， 0 2 所以 MA MB = ( 1+m2 ) y − y y − y = ( 1+m2 ) y2 − y ( y + y )+ y y 0 1 0 2 0 0 1 2 1 2 学科网（北京）股份有限公司( ) n2 2mn2 n2 −3 ( ) 3 3−3m = 1+m2 + + = 1+m2 ( 3−m)2 ( 3−m )( m2 −3 ) m2 −3 ( 3−m )( m2 −3 ) ( ) 3 m2 +1 = . m2 −3 故 MA MB 只与m有关. 19.（1）解：由题意得m2 +2mm+2，得−2m1. 因为m>0，所以m的取值范围为 ( 0,1 ] . { } （2）解：（方法一）数列 b 不是“稳定数列”. n 理由如下： 1 当n=1时，b =S = ； 1 1 4 1 当n2时，b =S −S = n（b 也成立）. n n n−1 4 1 1 1 1 1 1 ( ) 由题意得b2 +b b −b −b = (n+1)2 + n(n+2)− n− (n+2)= 2n2 −4n−7 ， n+1 n n+2 n n+2 16 16 4 4 16 1 ( ) 当n4时， 2n2 −4n−7 >0，即b2 +b b >b +b . 16 n+1 n n+2 n n+2 { } 故数列 b 不是“稳定数列”. n { } （方法二）数列 b 不是“稳定数列”. n 理由如下： 1 当n=1时，b =S = ； 1 1 4 1 当n2时，b =S −S = n（b 也成立）. n n n−1 4 1 25 24 6 9 当n=4时，b2 +b b −b −b = + −1− = >0， 5 4 6 4 6 16 16 4 16 即b2 +b b >b +b . 5 4 6 4 6 { } 故数列 b 不是“稳定数列”. n （3）证明：由c n 2 +1 +c n c n+2 c n +c n+2 ，得c n 2 +1 −1c n +c n+2 −c n c n+2 −1=( 1−c n )( c n+2 −1 ) ， 假设c >1,c >1，得c2 −1>0,c −1>0，则1−c >0. n+1 n+2 n+1 n+2 n 因为c >0，所以0<1−c <1<1+c ， n n n+2 学科网（北京）股份有限公司所以c2 −1 ( 1−c )( c −1 )<( 1+c )( c −1 )=c2 −1，即c 0,c −1>0，所以0<1−c <1<1+c ， n+2 n+1 n+3 n+1 则c2 −1 ( 1−c )( c −1 )<( 1+c )( c −1 )=c2 −1，即c 1，则c n 1,c n+2 1，则c n 2 +1 −1>0, ( 1−c n )( c n+2 −1 ) 0， 得c2 −1>( 1−c )( c −1 ) ，不符合题意，所以c 1. n+1 n n+2 n+1 故当n2时，T +2=c +c +c ++c +2c +c +1++1+2=c +c +n−2+2=T +n. n 1 2 3 n 1 2 1 2 2 学科网（北京）股份有限公司