2006年北京高考理科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_北京

2006 年北京高考理科数学真题及答案 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3 至9页，共150分。考试时间120分钟。考试结束，将本试卷和答题卡一并交回。 第Ⅰ卷（选择题 共40分） 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡。 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡 皮擦干净后，再选涂其他答案标号。不能答在试卷上。 一、 本大题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目 要求的一项。 1i （1） 在复平面内，复数 对应的点位于 i （A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限           （2）若a与bc都是非零向量，则“abac”是“a(bc)”的 （A）充分而不必要条件 （B）必要而不充分条件 （C）充分必要条件 （D）既不充分也不必要条件 （3）在1,2,3,4,5这五个数字组成的没有重复数字的三位数中，各位数字之和为奇数的共有 （A）36个 （B）24个 （C）18个 （D）6个 （4）平面的斜线AB交于点B，过定点A的动直线l与AB垂直，且交于点C，则 动点C的轨迹是 （A）一条直线 （B）一个圆 （C）一个椭圆 （D）双曲线的一支 (3a1)x4a,x1 （5）已知 f(x) 是(,)上的减函数，那么a的取值范围是 log x,x1  a 1 （A）(0,1) （B）(0, ) 3 1 1 1 （C）[ , ) （D）[ ,1) 7 3 7 （6）在下列四个函数中，满足性质：“对于区间 (1,2)上的任意 x ,x (x  x )， 1 2 1 2 | f(x ) f(x )||x x |恒成立”的只有 1 2 2 1 1 （A） f(x) （B） f x|x| x （C） f(x)2x （D） f(x) x2 第1页 | 共11页（7）设 f(n)224 27 210  23n10(nN)，则 f(n)等于  2 2 （A） (8n 1) （B） (8n11) 7 7 2 2 （C） (8n31) （D） (8n4 1) 7 7 （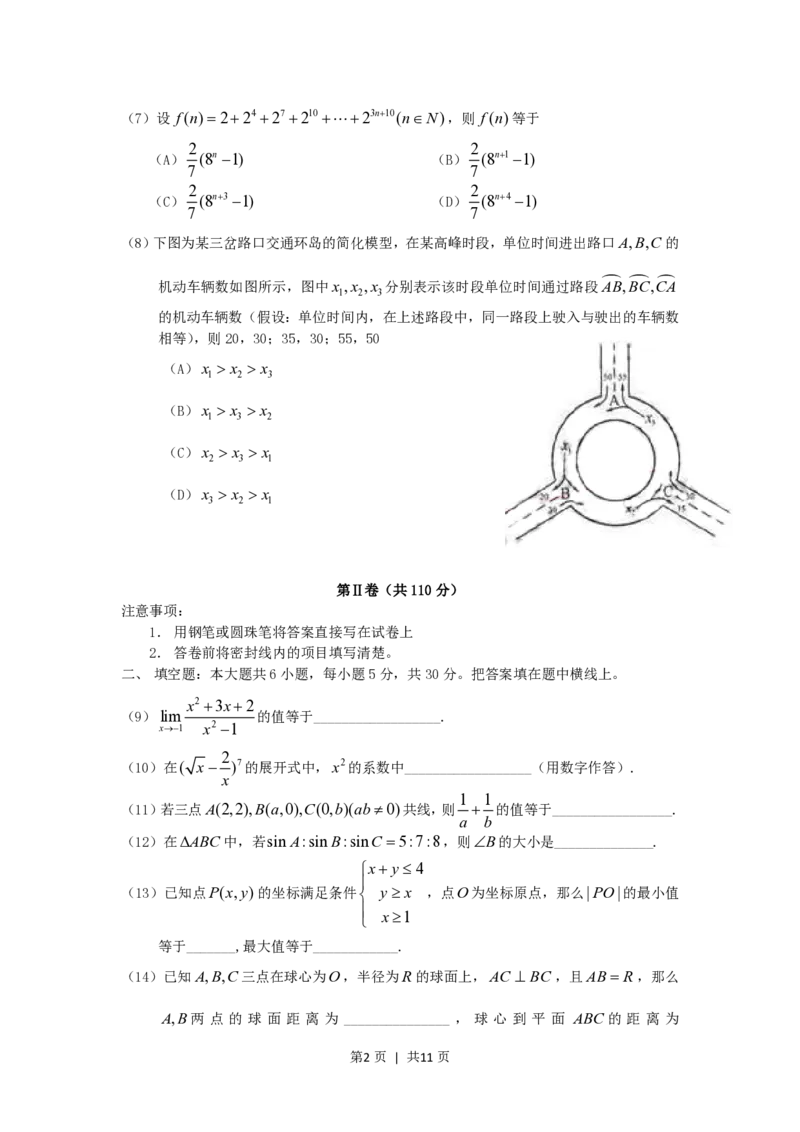8）下图为某三岔路口交通环岛的简化模型，在某高峰时段，单位时间进出路口A,B,C的 机动车辆数如图所示，图中x ,x ,x 分别表示该时段单位时间通过路段AB,BC,CA 1 2 3 的机动车辆数（假设：单位时间内，在上述路段中，同一路段上驶入与驶出的车辆数 相等），则20，30；35，30；55，50 （A）x  x  x 1 2 3 （B）x  x  x 1 3 2 （C）x  x  x 2 3 1 （D）x  x  x 3 2 1 第Ⅱ卷（共110分） 注意事项： 1．用钢笔或圆珠笔将答案直接写在试卷上 2．答卷前将密封线内的项目填写清楚。 二、 填空题：本大题共6小题，每小题5分，共30分。把答案填在题中横线上。 x2 3x2 （9）lim 的值等于__________________. x1 x2 1 2 （10）在( x  )7的展开式中，x2的系数中__________________（用数字作答）. x 1 1 （11）若三点A(2,2),B(a,0),C(0,b)(ab0)共线，则  的值等于_________________. a b （12）在ABC中，若sinA:sinB:sinC 5:7:8，则B的大小是______________. x y4  （13）已知点P(x,y)的坐标满足条件 y x ，点O为坐标原点，那么|PO|的最小值  x1  等于_______,最大值等于____________. （14）已知A,B,C三点在球心为O，半径为R的球面上，AC  BC ，且AB R，那么 A,B两 点 的 球 面 距 离 为 _______________ ， 球 心 到 平 面 ABC的 距 离 为 第2页 | 共11页______________. 三、 解答题：本大题共6小题，共80分。解答应写出文字说明，证明过程或演算步骤。 （15）（本小题共12分）  1 2sin(2x ) 4 已知函数 f(x) ， cosx （Ⅰ）求 f(x)的定义域； 4 （Ⅱ）设是第四象限的角，且tan ，求 f()的值. 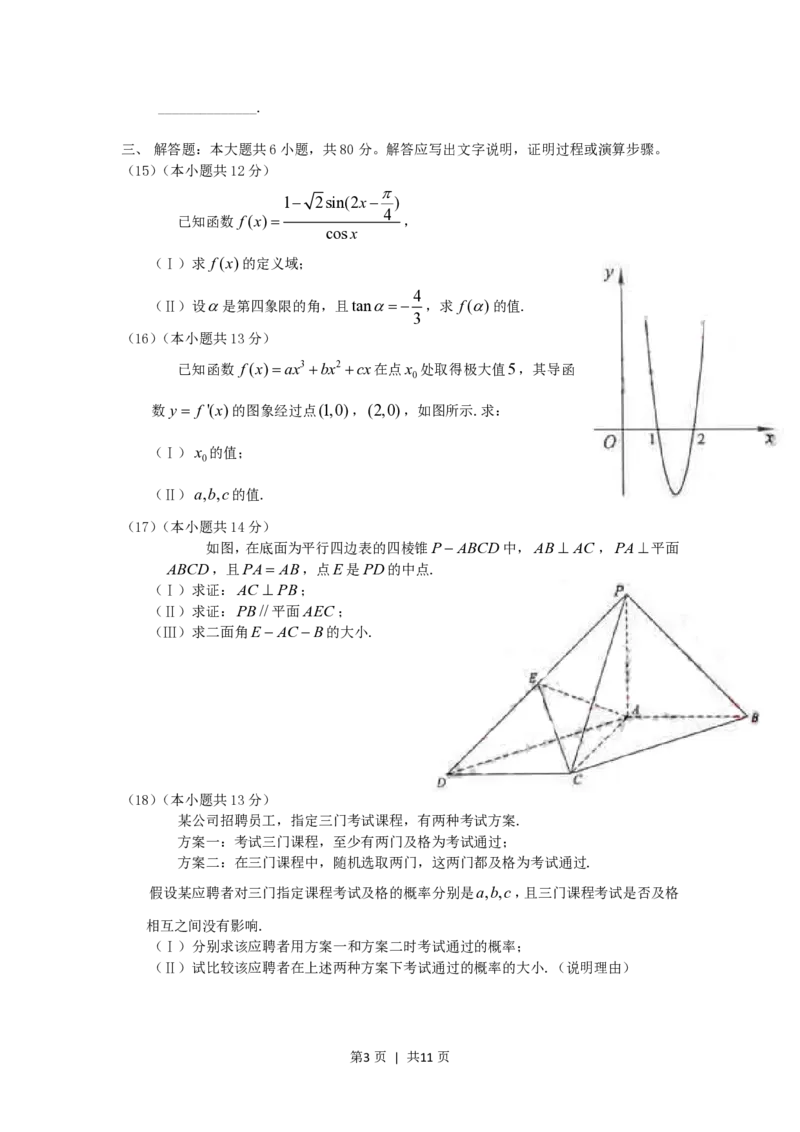3 （16）（本小题共13分） 已知函数 f(x)ax3 bx2 cx在点x 处取得极大值5，其导函 0 数y  f '(x)的图象经过点(1,0)，(2,0)，如图所示.求： （Ⅰ）x 的值； 0 （Ⅱ）a,b,c的值. 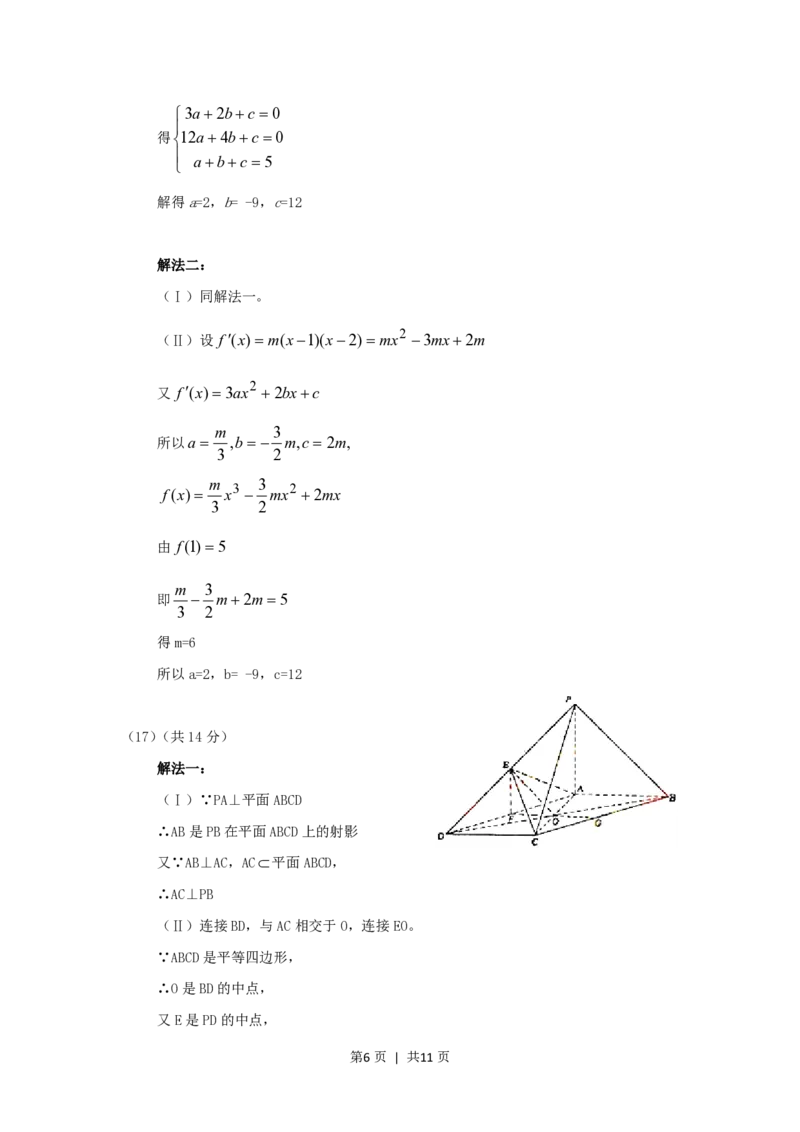（17）（本小题共14分） 如图，在底面为平行四边表的四棱锥PABCD中，AB AC，PA平面 ABCD，且PA AB，点E是PD的中点. （Ⅰ）求证：AC  PB； （Ⅱ）求证：PB//平面AEC； （Ⅲ）求二面角EACB的大小. （18）（本小题共13分） 某公司招聘员工，指定三门考试课程，有两种考试方案. 方案一：考试三门课程，至少有两门及格为考试通过； 方案二：在三门课程中，随机选取两门，这两门都及格为考试通过. 假设某应聘者对三门指定课程考试及格的概率分别是a,b,c，且三门课程考试是否及格 相互之间没有影响. （Ⅰ）分别求该应聘者用方案一和方案二时考试通过的概率； （Ⅱ）试比较该应聘者在上述两种方案下考试通过的概率的大小.（说明理由） 第3页 | 共11页（19）（本小题共14分） 已知点M(2,0),N(2,0)，动点P满足条件|PM ||PN |2 2.记动点P的轨 迹为W . （Ⅰ）求W 的方程；   （Ⅱ）若A,B是W 上的不同两点，O是坐标原点，求OAOB的最小值. （20）（本小题共14分） 在数列{a }中，若a ,a 是正整数，且a |a a |,n3,4,5, ，则称 n 1 2 n n1 n2  {a }为“绝对差数列”. n （Ⅰ）举出一个前五项不为零的“绝对差数列”（只要求写出前十项）； （ Ⅱ ） 若 “ 绝 对 差 数 列 ” {a }中 ， a 3,a 0， 数 列 {b }满 足 n 20 21 n b a a a ，n1,2,3, ，分别判断当n时，a 与b 的极限是 n n n1 n2  n n 否存在，如果存在，求出其极限值； （Ⅲ）证明：任何“绝对差数列”中总含有无穷多个为零的项. 2006年北京高考理科数学真题参考答案 一、选择题（本大题共8小题，每小题5分，共40分） （1）D （2）C （3）B （4）A （5）C （6）A （7）D （8）C 二、填空题（本大题共6小题，每小题5分，共30分） 1 （9） （10）－14 2 1  （1） （12） 2 3 1 3 （13） 2 10 （14） R R 3 2 三、解答题（本大题共6小题，共80分） 第4页 | 共11页（15）（共12分）  解：（Ⅰ）由cosx≠0得x  k (kZ) 2    故f(x)的定义域为x  k ,kZ  2  4 （Ⅱ）因为tana   ，且a是第四象限的角。 3 4 3 所以sina   ，cosa  5 5  1 2sin(2a ) 4 故 f(a)  cosa 2 2 1 2( sin2a cos2a) 2 2  cosa 1sin2acos2a  cosa 2cos2 a2sinacosa  cosa  2(cosasina) 14  5 （16）（共13分） 解法一： （Ⅰ）由图象可知，在（－∞，1）上 f (x) 0，在（1，2）上 f (x)0， 在（2，＋∞）上 f (x) 0 故 f(x)在（－∞，1），（2，＋∞）上递增，在（1，2）上递减。 因此 f(x)在x=1处取得极大值，所以x 1。 0 （Ⅱ） f(x)3ax2 2bxc 由 f (1) 0, f (2) 0, f(1) 5, 第5页 | 共11页3a2bc 0  得12a4bc 0  abc 5  解得a=2，b= -9，c=12 解法二： （Ⅰ）同解法一。 2 （Ⅱ）设 f (x)  m(x1)(x2)  mx 3mx2m 2 又 f (x) 3ax 2bxc m 3 所以a  ,b   m,c  2m, 3 2 m 3 3 2 f(x)  x  mx 2mx 3 2 由 f(1) 5 m 3 即  m2m 5 3 2 得m=6 所以a=2，b= -9，c=12 （17）（共14分） 解法一： （Ⅰ）∵PA⊥平面ABCD ∴AB是PB在平面ABCD上的射影 又∵AB⊥AC，AC平面ABCD， ∴AC⊥PB （Ⅱ）连接BD，与AC相交于O，连接EO。 ∵ABCD是平等四边形， ∴O是BD的中点， 又E是PD的中点， 第6页 | 共11页∴EO∥PB 又PB平面AEC，EO平面AEC， ∴PB∥平面AEC。 a b b （Ⅲ）取BC中点G，连接OG，则点G的坐标为( , ,0），OG＝（0，,0) 2 2 2 b b 又0E (0, , ),AC (a,0,0) 2 2 ∴0EAC 0,0GAC 0 ∴OE⊥AC，OG⊥AC ∴∠EOG是二面角E-AC-B的平面角。 0E0G 2 ∵cosEOG cos0E,0G    2 0E  0G ∴EOG 135 ∴二面角E AC B的大小为135 （18）（共13分） 解：记该应聘者对三门指定课程考试及格的事件分别为A，B，C，       则P A a,P B b,P C c （Ⅰ）应聘者用方案一考试通过的概率         p  P ABC P ABC P AB C P ABC 1        ab1c bc1a ac1b abc  abbcca2abc 应聘者用方案二考试通过的概率 1 1 1       p  P AB  P BC  P AC 2 3 3 3 1    abbcca 3 第7页 | 共11页  （Ⅱ）因为a,b,c 0,1 所以 2   p  p  abbcca 2abc 1 2 3 2         ab1c bc1a ca1b 0 3 故p  p 1 2 即采用第一种方案，该应聘者考试通过的概率较大。 （19）（共14分） 解法一： （Ⅰ）由 PM  PN 2 2知动点P的轨迹是以M，N为焦点的双曲线的右支，实 半轴长a  2 又半焦距c=2，故虚半轴长b c2 a2  2 x2 y2 所以W的方程为  1,x 2 2 2 （Ⅱ）设A，B的坐标分别为（x ,y ），（x ,y ） 1 1 2 2 当AB  x轴时,x  x ,y  y ,从而OA,OB  x x  y y  x2  y2  2 1 2 1 2 1 2 1 2 1 1 当AB与x 轴不垂直时，设直线AB的方程为y=kx+m，与W的方程联立，消去y得：   1k2 x2 2kmxm2 20 2km m2 2 故x  x  ,x x  1 2 1k2 1 2 k2 1 所以OAOB  x x  y y 1 2 1 2 第8页 | 共11页    x x  kx m kx m 1 2 1 2   1k2  x x km  x  x  m2 1 2 1 2    1k2 m2 2 2k2m2   m2 k2 1 1k2 2k2 2 4  2 k2 1 k2 1 又因为x x 0,所以k2 10,从而0A0B  2 1 2 综上，当AB  x轴时,OAOB取得最小值2。 解法二： （Ⅰ）同解法一。     （Ⅱ）设A，B的坐标分别为 x ,y , x ,y ，则 1 1 2 2 x2  y2   x  y  x  y   2  i 1,2  i i i i i i 令s  x  y ,t  x  y i i i i i i 则st 2,且s 0,t 0  i 1,2  ，所以 i i i i OAOB  x x  y y 1 2 1 2 1 1        s t s t  s t s t 4 1 1 2 2 4 1 1 2 2 1 1  s s  t t  s s t t  2 2 1 2 2 1 2 1 2 1 2  x  x 当且仅当s s t t ,即  1 2 时，“=”成立 1 2 1 2 y  y  1 2 所以OAOB的最小值是2。 （20）（共14分） （ Ⅰ ） 解 ： a 3,a 1,a  2,a 1,a 1,a  0,a 1,a 1,a  0,a 1 1 2 3 4 5 6 7 8 9 10 第9页 | 共11页（答案不惟一） （Ⅱ）解：因为绝对差数列 a 中,a 3,a  0，所以自第20项开始，该数列是 n 20 21 a 3,a 0,a 3,a 3,a 0,a 3,a 3,a 0, 。 20 21 22 23 24 25 26 27  即自第20项开始，每三个相邻的项周期地取值3，0，3，所以当n时，a的极 n 限不存在。 当n 20时,b  a a a 6,所以limb 6 n n n1 n2 n n （Ⅲ）证明：根据定义，数列 a 必在有限项后出现零项，证明如下： n 假设 a 中没有零项，由于a  a a ，所以对于任意的n，都有a 1，从而 n n n1 n2 n 当 a  a 时,a  a a  a 1  n 3  ； n1 n2 n n1 n2 n1 当a  a 时,a  a a  a 1  n 3  n1 n2 n n1 n2 n1 即a 的值要么比a 至少小1，那么比a 至少小1。 n n1 n2   a a  a , 令c n   a 2n1  a 2n1  a 2n  , n 1,2,3,  ,  2n 2n1 2n   则0c c 1n2,3,4, . n n1  由于c 是确定的正整数，这样减少下去，必然存在某项c<0，这与c>0 1 1 n （n=1,2,3,…）矛盾，从而 a 必有零项。 n   若第一次出现的零项为第n项，记a  A A0 ，则自第n项开始，每三个相 n1 邻的项周期地取值0，A，A即 a 0, n3k  a n3k1  A,k 0,1,2,3,  ,  a  A  n3k2 所以绝对差数列 a 中有无穷多个零的项。 n 第10页 | 共11页第11页 | 共11页