文档内容
合肥一中 2024~2025 学年度高三第二次教学质量检测
数学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.答题前,务必在答题卡和答题卷规定的地方填写自己的姓名、准考证号和座位号后两
位.
2.答题时,每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.
3.答题时,必须使用0.5毫米的黑色墨水签字笔在答题卷上书写,要求字体工整、笔迹清
晰.作图题可先用铅笔在答
.
题
.
卷
.
规定的位置绘出,确认后再用 0.5毫米的黑色墨水签字笔描
清楚.必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿
............. .... ..
纸
.
上
.
答
.
题
.
无
.
效
.
.
4.考试结束,务必将答题卡和答题卷一并上交.
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一
个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知集合M ={−2,−1,0,1,2 },N = { y y =log ( x2 +1 )} ,则图中阴影部分所表示的集合是( )
2
A.{−2,−1 } B.{−2,−1,0 }
C.{
0,1,2
} D.{−1,0 }
2.命题“∃x∈R,使x2 +x−1≠0”的否定是( )
A.∃x∈R,使x2 +x−1=0 B.不存在x∈R,使x2 +x−1≠0
C.∀x∉R,使x2 +x−1=0 D.∀x∈R,使x2 +x−1=0
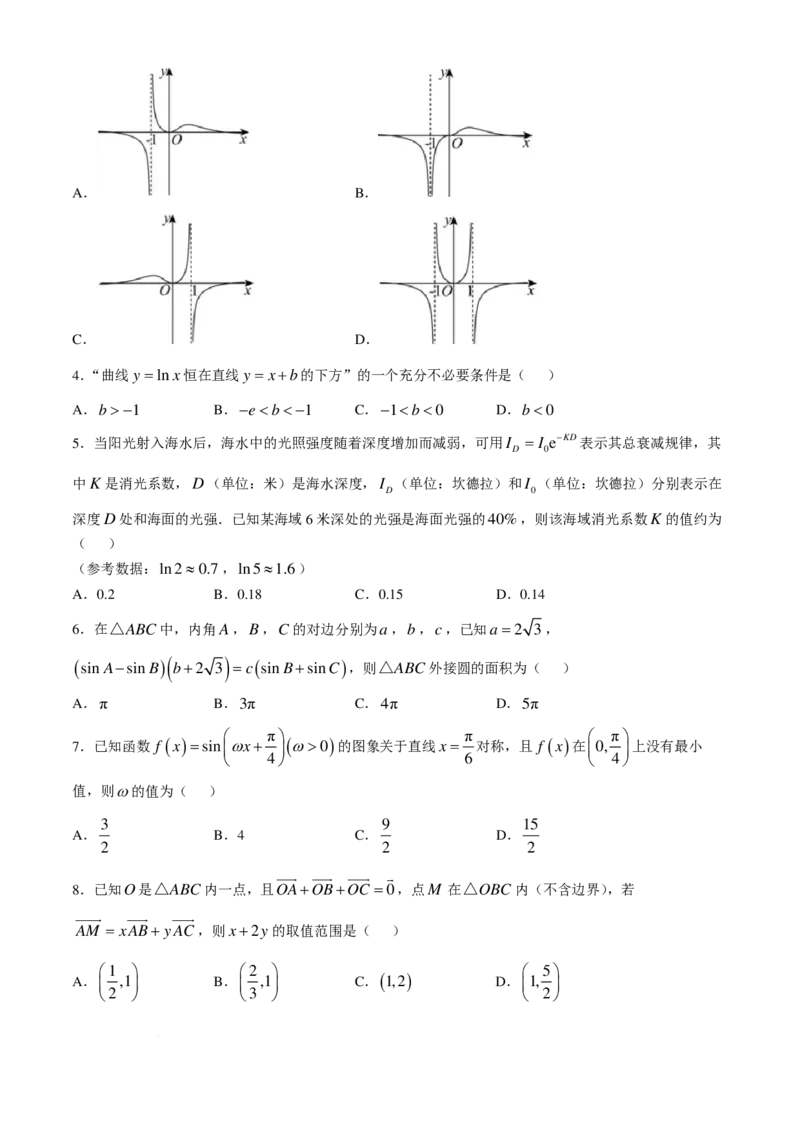
xsinx
3.函数 f ( x )= 的部分图象大致为( )
x3+1
学科网(北京)股份有限公司A. B.
C. D.
4.“曲线y =lnx恒在直线y = x+b的下方”的一个充分不必要条件是( )
A.b>−1 B.−e0 )的图象关于直线x= 对称,且 f ( x )在0, 上没有最小
4 6 4
值,则ω的值为( )
3 9 15
A. B.4 C. D.
2 2 2
8.已知O是△ABC内一点,且OA+OB+OC =0,点M 在△OBC内(不含边界),若
AM = xAB+ yAC,则x+2y的取值范围是( )
1 2 5
A. ,1 B. ,1 C.( 1,2 ) D.1,
2 3 2
学科网(北京)股份有限公司二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合
题目要求.全部选对得 6分,部分选对的得部分分,选对但不全的得部分分,有选错的得 0
分.
9.已知平面向量a =( 2,m ),b =( 1,−1 ),且 a+2b = a−2b ,则( )
π
A.m=2 B. a,b = C.a ⊥b D. a =2 2
3
10.已知b>1,若对任意的x∈( 1,+∞),不等式ax3+4x2 −abx−4b≤0恒成立,则( )
A.a<0 B.a2b=16
C.a2 +16b的最小值为32 D.a2 +ab+4a+b的最小值为−8
11.已知函数 f ( x )的定义域为R,函数F ( x )= f ( 1+x )−( 1+x )为偶函数,函数G ( x )= f ( 2+3x )−1
为奇函数,则下列说法正确的是( )
A.函数 f ( x )的一个对称中心为( 2,1 )
B. f ( 0 )=−1
C.函数 f ( x )为周期函数,且一个周期为4
D. f ( 0 )+ f ( 1 )+ f ( 2 )+ f ( 3 )+ f ( 4 )=5
三、填空题:本题共 3小题,每小题 5分,共 15分.
π 4
12.已知tan α+ =− ,则cos2α=______.
4 3
log x ,x>0
2
13.已知函数 f ( x )=1 ,方程 f ( x )=a有四个不同根x ,x ,x ,x ,且满足
x2 +x+2,x≤0 1 2 3 4
4
x x2( x +x )
x < x < x < x ,则 4 − 3 1 2 的最大值为______.
1 2 3 4 x 2
3
14.定义max { x,y }表示实数x,y中的较大者,若a,b,c是正实数,则
1 2 3
maxa, +maxb, +maxc, 的最小值是______.
b c a
四、解答题:本题共 5小题,第 15题满分 13分,第 16题、第 17题满分 15分,第 18题、
第 19题满分 17分,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)△ABC的内角A,B,C的对边分别为a,b,c,已知
学科网(北京)股份有限公司a2 +b2 −c2
( c−2b ) cosA+ =0.
2b
(1)若a =4,b+c=8,求△ABC的面积;
c
(2)若角C为钝角,求 的取值范围.
b
16.(15分)已知函数 f ( x )= xlnx+( a−1 ) x ( a∈R ).
1
(Ⅰ)当a =0时,关于x的方程 f ( x )=m在区间 ,3 内有两个不相等的实数根,求实数m的取值范
2
围;
1
(Ⅱ)求函数 f ( x )在区间
,e
上的最小值.
e
17.(15分)摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从
高处俯瞰四周景色.如图,某摩天轮最高点距离地面高度为120m,转盘直径为110m,设置有48个座
舱,开启后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,转一周大约需要30min.
(1)游客甲坐上摩天轮的座舱,开始转动tmin后距离地面的高度为Hm,求在转动一周的过程中,H 关
于t的函数解析式;
(2)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差h(单
位:m)关于t的函数解析式,并求高度差的最大值(精确到0.1m).
θ+ϕ θ−ϕ π π
参考公式:sinθ+sinϕ=2sin cos .参考数据:sin ≈0.2079,sin ≈0.0654.
2 2 15 48
18.(17分)
已知函数 f ( x )=sinx.
(1)当x≥0时, f ( x )≤ax,求实数a的取值范围;
π
(2)若0<α<β< ,求证: f (β)− f (α)<(β−α) cosα;
2
(3)若n∈ *,a =0,a ,a ,,a 为正实数,且a +a ++a =1,求证:
0 1 2 n 1 2 n
学科网(北京)股份有限公司n a π
1≤∑ i < .
1+a +a ++a a +a ++a 2
i=1 0 1 i−1 i i+1 n
19.(17分)
{ }
已知实数集X ={ x ,x ,,x },定义:X ⊗X = x x x ,x ∈X (x 与x 可以相同).记 X 为集合
1 2 n i j i j i j
X 中的元素个数.
(1)若X ={ 1,2,3,6 },请直接给出X ⊗X 和 X ⊗X ;
(2)若x ,x ,,x 均为正数,且 X ⊗X =300,求 X 的最小值;
1 2 n
(3)若 X =11,求证: X ⊗X ≥17.
合肥一中 2024~2025 学年度高三第二次教学质量检测
数学参考试卷
1.A
【详解】N = { y y≥0 } ,所以阴影部分M ( N )={−2,−1 }.故选:A.
R
2.D
【详解】命题“∃x∈R,使x2 +x−1≠0”的否定是∀x∈R,使x2 +x−1=0.故选:D.
3.A
xsinx
【详解】易知函数 f ( x )= 的定义域为 { x x≠−1 } ,故可排除C,D;
x3+1
π π 2
− sin − π
π π 4 4 8
又− >−1, f − = = >0,所以可排除B,故选:A.
4 4 π 3 π 3
−
+1
−
+1
4 4
4.C
【详解】由曲线y =lnx恒在直线y = x+b下方,可得lnx< x+b,
b>lnx−x恒成立,即b>−1
所以“曲线y =lnx恒在直线y = x+b的下方”的充要条件是b>−1,故选:C.
5.C
I 2
【详解】依题意得, D =40%=e−6K,化成对数式,−6K =ln =ln2−ln5≈−0.9,
I 5
0
解得,K ≈0.15.故选:C.
6.C
学科网(北京)股份有限公司( )
【详解】因为a =2 3,且( sinA−sinB ) b+2 3 =c ( sinB+sinC ),
所以( sinA−sinB )( a+b )=c ( sinB+sinC ),
由正弦定理,可得( a−b )( a+b )=c ( b+c ),即a2 =b2 +c2 +bc,
b2 +c2 −a2 1 2π
所以cosA= =− ,又因A∈( 0,π ),所以A= ,
2bc 2 3
a 2 3
所以△ABC外接圆的半径为 = =2.S =π⋅22 =4π.故选:C.
2sinA 3
2×
2
7.A
π π π π π
【详解】由 f ( x )=sin ωx+ (ω>0 )的图象关于直线x= 对称可得ω + =± +kπ,k∈Z,
4 6 6 4 2
3 9
解得ω= +6k或ω=− +6k,k∈Z,
2 2
π π 5π 3
由于 f ( x )在0, 上没有最小值,所以 ≤ ⇒0<ω≤5,所以ω= ,故选:A.
4 4 4ω 2
8.C
【详解】因为△ABC内一点,OA+OB+OC =0,
所以O为△ABC的重心,
又M 在△OBC内(不含边界),且当M 与O重合时,x+2y最小,
2 1( ) 1 1
此时AM =λAB+µAC = ×
AB+ AC
= AB+ AC
3 2 3 3
1
所以x= y = ,即x+2y =1,
3
当M 与C重合时,x+2y最大,
此时AM = AC,
所以x=0,y =1,即x+2y =2,
因为M 在△OBC内且不含边界,
所以取开区间,即x+2y∈(
1,2
),故选:C.
二.多选题
学科网(北京)股份有限公司9.ACD
【详解】由a =( 2,m ),b =( 1,−1 ),
可得a+2b =( 4,m−2 ),a−2b =( 0,m+2 ),
由 a+2b = a−2b ,可得16+( m−2 )2 =( m+2 )2 ,
解得m=2,故A正确;
由a =( 2,2 ),可得 a = 4+4 =2 2,故D正确;
a⋅b 2−2
又cos a,b = = =0,
a b 2 2× 2
π
则 a,b = ,a ⊥b ,故B错误,C正确.故选:ACD.
2
10.ABD
【详解】因为ax3+4x2 −abx−4b≤0,即( ax+4 )( x2 −b ) ≤0恒成立,
又因为b>1,x>1,
所以当1< x< b时,x2 −b<0,当x> b 时,x2 −b>0,
因为对任意的x∈( 1,+∞),不等式ax3+4x2 −abx−4b≤0恒成立,
所以当0< x< b时,ax+4≥0,当x> b 时,ax+4≤0,
所以对于函数y =ax+4,必有a<0,单调递减,且零点为x= b ,
所以a b +4=0,所以a2b=16,
所以A正确,B正确;
4
对于C,因为a b +4=0,所以a=− ,
b
16 16
所以a2 +16b= +16b≥2 ⋅16b =32,
b b
16
当且仅当 =16b,即b=1时取等号,与条件不符,所以C错误;
b
16 16 16 16
对于D,a2 +ab+4a+b= −4 b − +b= +b − 4 b +
b b b b
学科网(北京)股份有限公司2
16 4 4 4
= +b −4 b + = b + −4 b + −8,
b b b b
4
令m= b + ,则m≥4,当且仅当b=4时,等号成立.
b
则原式=m2 −4m−8 ( m≥4 ),
由二次函数的性质可得y =m2 −4m−8 ( m≥4 )的最小值为−8,
此时b=4,a=−2,所以D正确,故选:ABD.
11.ABD
【详解】对于A,因为G ( x )= f ( 2+3x )−1为奇函数,所以G (−x )=−G ( x ),
即 f ( 2−3x )−1=−
f ( 2+3x )−1
,所以 f ( 2−3x )+ f ( 2+3x )=2,
所以 f ( 2−x )+ f ( 2+x )=2,所以函数 f ( x )的图象关于点( 2,1 )对称,所以A正确,
对于B,在 f ( 2−x )+ f ( 2+x )=2中,令x=0,得2f ( 2 )=2,得 f ( 2 )=1,
因为函数F ( x )= f ( 1+x )−( 1+x )为偶函数,所以F (−x )= F ( x ),
所以 f ( 1−x )−( 1−x )= f ( 1+x )−( 1+x ),所以 f ( 1+x )− f ( 1−x )=2x,
令x=1,则 f ( 2 )− f ( 0 )=2,所以1− f ( 0 )=2,得 f ( 0 )=−1,所以B正确,
对于C,因为函数 f ( x )的图象关于点( 2,1 )对称, f ( 0 )=−1,
所以 f ( 4 )=3,所以 f ( 0 )≠ f ( 4 ),所以4不是 f ( x )的周期,所以C错误,
对于D,在 f ( 2−x )+ f ( 2+x )=2中令x=1,则 f ( 1 )+ f ( 3 )=2,
令x=2,则 f ( 0 )+ f ( 4 )=2,因为 f ( 0 )=−1,所以 f ( 4 )=3,
因为 f ( 2 )=1,所以 f ( 0 )+ f ( 1 )+ f ( 2 )+ f ( 3 )+ f ( 4 )=5,所以D正确,故选:ABD.
三.填空题(共 1小题)
24
12.− .
25
π 4
【详解】因为tan α+ =− ,
4 3
tanα+1 4
所以 =− ,可得tanα=7,
1−tanα 3
学科网(北京)股份有限公司cos2α−sin2α 1−tan2α 1−72 24
则cos2α= = = =− .
cos2α+sin2α 1+tan2α 1+72 25
24
故答案为:− .
25
129
13. .
8
x +x
【详解】作出函数图像可得 1 2 =−2,−log x =log x
2 2 3 2 4
1
从而得x x =1,且−log x ∈( 1,2 ],从而得 ∈( 2,4 ],
3 4 2 3 x
3
1 x2( x +x ) 1
∴原式= − 3 1 2 = +2x2,
x2 2 x2 3
3 3
1 1 1
令 y = +2x2, ∈( 2,4 ],∴ ∈( 4,16 ],
x2 3 x x2
3 3 3
1 2
令t = ,则 f ( t )=t+ ,t∈( 4,16 ],
x2 t
3
( ) 9 129
f ( t )在 2,+∞ 单调递增,∴ f ( t )∈ , ,
2 8
129
∴最大值为 .
8
14.2 5
3 3 1 2 3
【详解】按c≤ 和c≥ 分类:记M =maxa, +maxb, +maxc, ,
a a b c a
3 2 3 2a 3 5a 3 5a 3
当c≤ 时,M ≥a+ + ≥a+ + = + ≥2 ⋅ =2 5,
a c a 3 a 3 a 3 a
学科网(北京)股份有限公司3 2
当且仅当a= ,b= ,c= 5时,等号成立;
5 5
3 2 3 2 5 5
当c≥ 时,M ≥a+ +c≥ + +c= +c≥2 ⋅c =2 5,
a c c c c c
3 2
当且仅当a= ,b= ,c= 5时,等号成立.
5 5
综上所述,M 的最小值是2 5.
四.解答题
15.(13分)【详解】(1)由( c−2b ) cosA+acosC =0和正弦定理得,
( sinC−2sinB ) cosA+sinAcosC =0,
因sinCcosA+sinAcosC =sin ( A+C )=sin ( π−B )=sinB,
则有sinB ( 1−2cosA )=0,
1 π
因0< B<π,sinB>0,则cosA= ,又0< A<π,故A= .
2 3
由余弦定理,a2 =b2 +c2 −2bccosA,代入得,b2 +c2 −bc=16,
因b+c=8,则有( b+c )2 −3bc=16,即得bc=16,
1 1 3
故△ABC的面积S = bcsin A= ×16× =4 3.
2 2 2
b c c sinC 2π
(2)由正弦定理, = 可得 = ,因C = −B,
sinB sinC b sinB 3
2π 3 1
sin −B cosB+ sinB
c sinC 3 2 2 3 1
代入化简得: = = = = + .
b sinB sinB sinB 2tanB 2
π
0< B<
2 π
因C为钝角,故由 可得0< B< ,
2π π 6
−B>
3 2
3 3 3 c c
则0 ,即 >2,故 的取值范围是( 2,+∞).
3 2tanB 2 b b
学科网(北京)股份有限公司16.(15分)【详解】(Ⅰ)当a =0时, f ( x )= xlnx−x, f′( x )=lnx+1−1=lnx,
f′( x )>0 lnx>0 f′( x )<0
1
∴由1 ⇔ 1 ⇔1< x≤3,1 ⇔ ≤ x<1,
≤ x≤3
≤ x≤3
≤ x≤3 2
2 2 2
故可列表:
1 1
x ,1 1 ( 1,3 ) 3
2 2
y′ − 0 +
1 1
y − ln2− −1 3ln3−3
2 2
1 1
− ln2− <0<3ln3−3,
2 2
1 1 1
∴关于x的方程 f ( x )=m在区间
,3
内有两个不相等的实数根时−10 ),由 f′( x )=0得x=e−a.
1 1
①当e−a < ,即a>1时, f′( x )>0, f ( x )在
,e
上为增函数,
e e
1 a−2
f ( x ) = f = ;
min e e
1 1
②当 ≤e−a ≤e,即−1≤a≤1时,在
,e−a
上 f′( x )<0, f ( x )为减函数,
e e
在
e−a,e
上 f′( x )>0, f ( x )为增函数, f ( x ) = f ( e−a ) =−e−a;
min
1
③当e−a >e,即a<−1时, f′( x )<0, f ( x )在
,e
上为减函数, f ( x ) = f ( e )=ea.
e min
a−2
,a >1
e
综上所述, f ( x ) =−e−a,−1≤a≤1.
min
ea,a<−1
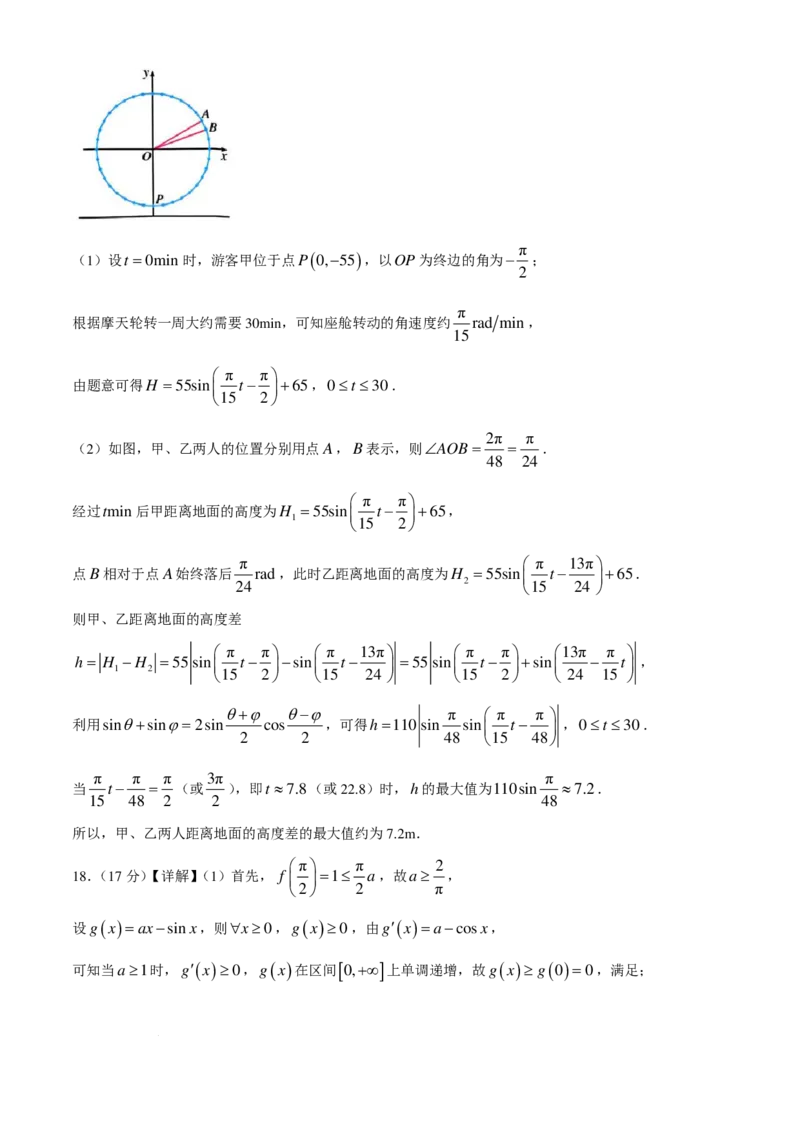
17.【详解】如图,设座舱距离地面最近的位置为点P,以轴心O为原点,与地面平行的直线为x轴建立
直角坐标系.
学科网(北京)股份有限公司π
(1)设t =0min时,游客甲位于点P ( 0,−55 ),以OP为终边的角为− ;
2
π
根据摩天轮转一周大约需要30min,可知座舱转动的角速度约 rad min,
15
π π
由题意可得H =55sin t− +65,0≤t ≤30.
15 2
2π π
(2)如图,甲、乙两人的位置分别用点A,B表示,则∠AOB= = .
48 24
π π
经过tmin后甲距离地面的高度为H =55sin t− +65,
1 15 2
π π 13π
点B相对于点A始终落后 rad,此时乙距离地面的高度为H =55sin t− +65.
24 2 15 24
则甲、乙距离地面的高度差
π π π 13π π π 13π π
h= H −H =55sin t− −sin t− =55sin t− +sin − t ,
1 2 15 2 15 24 15 2 24 15
θ+ϕ θ−ϕ π π π
利用sinθ+sinϕ=2sin cos ,可得h=110 sin sin t− ,0≤t ≤30.
2 2 48 15 48
π π π 3π π
当 t− = (或 ),即t ≈7.8(或22.8)时,h的最大值为110sin ≈7.2.
15 48 2 2 48
所以,甲、乙两人距离地面的高度差的最大值约为7.2m.
π π 2
18.(17分)【详解】(1)首先, f =1≤ a,故a≥ ,
2 2 π
设g ( x )=ax−sinx,则∀x≥0,g ( x )≥0,由g′( x )=a−cosx,
可知当a≥1时,g′(
x
)≥0,g (
x
)在区间[ 0,+∞]上单调递增,故g (
x
)≥
g
(
0
)=0,满足;
学科网(北京)股份有限公司2 π π
当 ≤a<1时,由g′( x )在区间0, 上单调递增,且g′( 0 )=a−1<0,g′ =a>0,
π 2 2
π
故存在x ∈ 0, ,使得g′( x )=0,且x∈( 0,x )时,g′( x )<0,g ( x )单调递减,
0 2 0 0
此时,g ( x )< g ( 0 )=0,与题设矛盾.
综上所述,实数a的取值范围[ 1,+∞).
(2) f (β)− f (α)<(β−α) cosα⇔ f (β)−βcosα< f (α)−αcosα
π
由0<α<β< ,可知βcosα>βcosβ,即 f (β)−βcosα< f (β)−βcosβ
2
故只要证 f (β)−βcosβ< f (α)−αcosα
π
设g ( x )= f ( x )−xcosx,x∈ 0, ,则g′( x )=cosx−( cosx−xsinx )= xsinx>0,
2
π
在g ( x )区间0, 上单调递增,即g (α)< g (β),
2
f
(β)−βcosβ<
f
(α)−αcosα,故原不等式成立.
(3)一方面,由于a =0 z y >> z y > z y > z y >> z y 是X ⊗X 中的k+l−1=10个元素,且非正数;
1 1 1 2 1 k 2 k 3 k l k
学科网(北京)股份有限公司又 y y < y y < y y < y y < y y < y y < y y 是X ⊗X 中的7个元素,且为正数,
2 3 2 4 2 5 2 6 3 6 4 6 5 6
故X ⊗X 中元素不少于17个,
即 X ⊗X ≥17;
{ } { }
另外,当X = 0,±1,±2,±22,±23,±24 时,X ⊗X = 0,−1,±2,±22,±23,±24,±25,±26,±27,−28
满足 X ⊗X =17,
故 X ⊗X ≥17.
学科网(北京)股份有限公司