数学答案_2024-2025高三（6-6月题库）_2025年02月试卷_02142025年2月浙江G12名校协作体高三返校考

2024 学年第二学期浙江省名校协作体适应性试题
高三年级数学学科
考生须知：
1．本卷满分 150分，考试时间 120分钟；
2．答题前，在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号；
3．所有答案必须写在答题卷上，写在试卷上无效；
4．2024学年第二学期浙江省名校协作体联考将于 2.13进行，本卷仅供模拟训练使用．
一、选择题：本大题共 8小题，每小题 5分，共40分．在每小题给出的四个选项中，只有一
项是符合题目要求的．
z 
1. 复数z  2i（i为虚数单位），则 （ ）
A.1 B. 2 C. 3 D. 5
【答案】D
【解析】
【分析】由复数模的定义计算．
【详解】由已知 z  22(1)2  5 ．
故选：D．
2. 设集合S {x|2 x2}，A{x∣xS}，B   x∣2 xS  ，则AB （ ）
A. {0} B. {1} C. {0,1} D. {x|0 x 2}
【答案】D
【解析】
【分析】根据集合的描述法确定集合A,B，再根据集合的交集运算即可得答案.
【详解】因为集合S {x|2 x2}，则A x∣xS {x|2 x2}，
所以B   x2 |xS   x|0 x4  ，
则AB {x|0 x 2}.
故选：D.
    
3. 已知向量a (1,4)，b (x,2)，若a//(3ab)，则x（ ）
第1页/共22页
学科网（北京）股份有限公司1
A. 1 B.  C. 1 D.1
2 2
【答案】C
【解析】
【分析】根据给定条件，利用向量线性运算的坐标表示，及共线向量的坐标表示求出参数.
      
【详解】向量a (1,4)，b (x,2)，则3ab (3x,10)，而a//(3ab)，
1
所以4(3x)10，解得x .
2
故选：C
π
4. 某圆台的上、下底面半径分别为2和4，母线与底面的夹角为 ，则该圆台的侧面积为（ ）
4
A. 12 2π B. 12π C. 6 2π D. 6π
【答案】A
【解析】
【分析】根据条件求出圆台的母线长，结合圆台侧面积公式可得结果.
【详解】设圆台的上底面半径为r ，下底面半径为R，母线长为l，则r =2,R=4，
R-r
l = = 2 2
由题意得， π ，
cos
4
∴该圆台的侧面积S = πl ( r+R )=12 2π.
故选：A.
1
5. 已知随机变量X服从二项分布B(3, )，则P(X  E(X))（ ）
3
1 7 20 26
A. B. C. D.
27 27 27 27
【答案】B
【解析】
【分析】利用二项分布的期望公式求出期望，再利用二项分布的概率公式求出概率.
1 1
【详解】由随机变量X服从二项分布B(3, )，得E(X)3 1，
3 3
1 2 1 7
所以P(X  E(X)) P(X 1)C2( )2 C3( )3  .
3 3 3 3 3 27
故选：B
第2页/共22页
学科网（北京）股份有限公司π   π 
6. 方程sin cosx cos sin x 在  0,π  上的实数解有（ ）
2  2 
A.1个 B.2个 C.3个 D.4个
【答案】B
【解析】
π  π π 
【分析】利用分类讨论思想，先对特殊值0，,π进行分析判断，然后再对x 0， 和x  ,π进行分
2  2 2 
析判断即可得解.
π  π  π 
【详解】当x0时，sin cos0 sin =1，cos sin0=cos0=1，
2  2 2 
π   π 
满足方程sin cosx cos sin x ，所以x0是方程的一个实数解；
2  2 
π π π  π π π
当x 时，sin cos  sin0=0，cos sin =cos =0 ，
2 2 2 2 2 2
π   π  π
满足方程sin cosx cos sin x ，所以x 也是方程的一个实数解；
2  2  2
π   π  π 
当x π时，sin cosπ sin  =1，cos sin π =cos0=1，
2   2 2 
π   π 
不满足方程sin cosx cos sin x，所以x π不是方程的一个实数解；
2  2 
 π π  π π  π
当x 0， 时， cosx 0, , sinx 0, ,
 2 2  2 2  2
π   π  π π π
由方程sin cosx cos sin x可得： cosx sinx ，
2  2  2 2 2
 π 2
即cosxsinx1sinx

 ，
 4 2
 π
由于x 0， ，所以此时方程无解；
 2
π  π  π  π  π
当x  ,π时， cosx   ,0, sinx 0, ,
2  2  2  2  2
第3页/共22页
学科网（北京）股份有限公司π   π 
此时sin cosx 0,cos sinx 0 ，
2  2 
π   π 
显然方程sin cosx cos sin x 无解；
2  2 
π   π  π
故综上，方程sin cosx cos sin x 只有2个解，分别为0， .
2  2  2
故选：B.
7. 设抛物线C：x2 4y的焦点为F，过点(0,6)的一条直线交C于A，B两点．若 AF 10，则 BF （ ）
A.3 B.4 C.5 D.6
【答案】C
【解析】
【分析】设出直线AB的方程，与抛物线方程联立，结合已知及抛物线定义求出A,B的纵坐标即可.
【详解】直线AB的斜率存在，设其方程为ykx6，A(x ,y ),B(x ,y )，
1 1 2 2
y kx6 x2 x2
由 消去y得x2 4kx240，则x x  24，y y  1  2 36，
x2 4y 1 2 1 2 4 4
抛物线C：x2 4y的准线方程为 y 1，由 AF 10，得 y 110，解得 y 9，
1 1
因此 y 4，所以 BF  y 15.
2 2
故选：C
8. 在等腰梯形ABCD中，AD//BC．设P是其内部一点，满足PA1，PB 2，PC 3，PD 4，
AD
则 （ ）
BC
A. 2 B. 3 C.2 D.3
【答案】D
【解析】
【分析】建立直角坐标系，利用两点的距离公式求解即可.
【详解】由题意，以BC中点为原点，BC所在直线为x轴建立如图所示坐标系，
第4页/共22页
学科网（北京）股份有限公司设P  x,y  ，A a,h  ，B b,0  ，C  b,0  ，D  a,h  ，其中a,b,h0，
则由题意可得 xa 2  yh 2 1①， xb 2  y2 4②，
 xb 2  y2 9③， xa 2  yh 2 16④，
a
④①得4ax15，③②得4bx5，所以 3，
b
AD 2a a
所以   3，
BC 2b b
故选：D
二、选择题：本题共 3小题，每小题 6分，共 18分．在每小题给出的选项中，有多项符合题
目要求．全部选对的得 6分，部分选对的得部分分，有选错的得 0分．
9. 为得到函数 yln  ex  的图象，可将函数 ylnx的图象（ ）
A. 向上平移一个单位长度 B. 向下平移一个单位长度
1
C. 纵坐标不变，横坐标伸长为原来的e倍 D. 纵坐标不变，横坐标缩短为原来的 倍
e
【答案】AD
【解析】
【分析】根据函数图象变换可得结果.
1
【详解】由题意可得，函数 ylnx的图象纵坐标不变，横坐标缩短为原来的 ，可得到函数yln  ex  的
e
图象，故选项C错误，选项D正确.
∵ y ln  ex lnx1，
∴将函数 ylnx的图象向上平移一个单位长度可得到函数 yln  ex  的图象，故选项A正确，选项B错
误.
故选：AD.
10. 在正三棱柱ABCABC 中，AB2，AA 3，点D、E分别在棱BB、CC上运动（D不与B 重
1 1 1 1 1 1 1
合，E不与C 重合），使得△ADE是等腰三角形．记△ADE的面积为S，平面ADE与平面ABC所成
1 1 1 1
第5页/共22页
学科网（北京）股份有限公司锐二面角的平面角大小为，则（ ）
A. DE//平面ABC B. △ADE可能为等腰直角三角形
1 1 1 1
( ù  
C. S的取值范围是 3,2 3úû D. 的取值范围是0, 
 3
【答案】BCD
【解析】
  
【分析】取BC 的中点O，则AO  BC ，以点O为坐标原点，OA、OB、AA 的方向分别为x、y、z轴
1
的正方向建立空间直角坐标系，设点D  0,1,d  、E  0,1,e  ，其中0d 3，0e3，分AD AE、
1 1
AD  DE、AE  DE三种情况讨论，结合空间向量法逐项分析，即可得出结果.
1 1
【详解】在正三棱柱ABCABC 中，取BC的中点O，则AO  BC，
1 1 1
  
以点O为坐标原点，OA、OB、AA 的方向分别为x、y、z轴的正方向建立空间直角坐标系，
1
  
则A 3,0,3 、B  0,1,3  、C  0,1,3  ，则BC  0,2,0 ，
1 1 1 1 1
设点D  0,1,d  、E  0,1,e  ，其中0d 3，0e3.
在正三棱柱ABCABC 中，△ABC 为等边三角形，
1 1 1 1 1 1
因为△ADE为等腰三角形，有三种情况：①AD AE；②AD  DE；③AE  DE.
1 1 1 1 1
 
①若AD AE， AD  4 d 3 2 ， AE  4 e3 2 ，
1 1 1 1
 
由 AD  AE 可得 d 3 2  e3 2，即  d e  d e6 0，
1 1
 
由已知0d e6，故d e，此时DE  0,2,0 BC ，则DE//BC ，
1 1 1 1
DE平面ABC ，BC 平面ABC ，则DE//平面ABC ，
1 1 1 1 1 1 1 1 1 1 1
  
因为 AE  AD  4 d 3 2  2 DE ，此时，△ADE不可能是等腰直角三角形；
1 1 1
第6页/共22页
学科网（北京）股份有限公司 
线段DE的中点为M  0,0,d  ， AD  AE ，M 为DE的中点，则AM  DE，
1 1 1
 A  M   3 d 3 2   3,2 3，S  1 D  E    A  M    A  M    3,2 3；
1  2 1 1 
  
 
设平面ADE的法向量为m x,y,z ，AM   3,0,d 3 ，DE  0,2,0 ，
1 1


 mDE 2y 0 
 
由  ，取xd 3，可得m d 3,0, 3 ，
 m  AM  3x d 3  z 0
1

平面ABC的一个法向量为n 0,0,1 ，因为3d 30，
 
mn
3 1   
cos      ,1，为锐角，则  , ；
m  n  d 3 2 3 2  3 2
 
②若AD  DE， AD  4 d 3 2 ， DE  4 d e 2 ，
1 1
 
由 AD  DE 可得 d 3 2  d e 2，可得  e3  2d e3 0，
1
0d 3 3
因为e3，则e2d 3，由 ，可得 d 3，则32d 60
0e2d 33 2
  uuuur
DE  0,2,d 3 ，此时DE与BC 不平行，
1 1
若DE//平面ABC ，DE 平面BBCC，平面BBCC平面ABC BC ，则DE//BC ，矛盾，
1 1 1 1 1 1 1 1 1 1 1 1 1 1
故假设不成立，即DE与平面ABC 不平行；
1 1 1
 
 
若△ADE为等腰直角三角形，AD   3,1,d 3 ，DE  0,2,d 3 ，
1 1
第7页/共22页
学科网（北京）股份有限公司 
则ADDE  d 3 2 20，解得d 3 2或3 2 （舍），
1
此时△ADE可能为等腰直角三角形；
1
 3 1 
取线段AE的中点N ，连接DN，则DN  AE ，且N , ,d，
1 1   2 2  
 D  N      3   2     1 1   2  3，  A  1  E   44  d 3 2  4 2d 6 2  2, 13  ，
 2   2 
1   3   39 
所以，S  DN  AE  AE  3, ；
2 1 2 1   2 
    3 3 
设平面ADE的法向量为m x,y,z ，DE  0,2,d 3 ，DN  , ,0，
1   2 2  

m  DE 2y d 3  z 0
   
由   3 3 ，取x 3  d 3 ，可得m 3  d 3  ,d 3,2 ，
mDN  x y0
 2 2

平面ABC的一个法向量为n
0,0,1
，
 
mn 2 1 2 13 
cos       ,1，

m  n 2  d 3 2 1  d 3 2 1  13 
2 13 1  
因为  ，此时的取值范围是0,  的真子集.
13 2  3
③若AE  DE，同②.
1
第8页/共22页
学科网（北京）股份有限公司综上所述，对于A选项，DE与平面ABC 不一定平行，A错；
1 1 1
对于B选项，△ADE可能为等腰直角三角形，B对；
1
( ù
对于C选项，S的取值范围是 3,2 3úû ，C对；
 
对于D选项，的取值范围是0,

，D对.
 3
故选：BCD.
【点睛】方法点睛：求二面角常用的方法：
（1）几何法：二面角的大小常用它的平面角来度量，平面角的作法常见的有：
①定义法；②垂面法，注意利用等腰三角形的性质；
（2）空间向量法：分别求出两个平面的法向量，然后通过两个平面法向量的夹角得到二面角的大小，但要
注意结合实际图形判断所求二面角是锐角还是钝角.
11. 观察下面一组等式：
13 1
23 35
33 7911
43 13151719
…=…
记a
i,j
表示第i个等式中等号右边第j个数，如a
3,2
9，a
4,3
17，则（ ）
 
A 2025 a jN* B. a n2 n1
. 45,j n,1
 100 1  1  a 120
C. D. i,j
i10 a i,2 9 ij8
【答案】ACD
【解析】
【分析】通过分析计算a
n,1
和a
n,n
，即可确定选项A正确，选项B错误；根据a
i,1
计算a
i,2
，利用放缩
 a a a a a
及裂项相消法可得选项C正确；通过分析可知 i,j 4,4 5,3 6,2 7,1，计算各项可得选项D
ij8
正确.
【详解】由题意得，所有等式等号右边的数构成以1为首项，2为公差的等差数列，
第9页/共22页
学科网（北京）股份有限公司第n个等式等号右边为n个连续奇数的和，
n  n1 
前n1个等式等号右边共有123 n1  个奇数，
2
n  n1 
∴a 12 n2 n1，a a 2  n1 n2n1，选项B错误.
n,1
2
n,n n,1
∵a 452 4511981,a 4524512069 ，
45,1 45,45
 
∴2025 a jN* ，选项A正确.
45,j
∵a i2 i1，∴a a 2i2i3i2i ，
i,1 i,2 i,1
1 1 1 1
  
∴ ，
a i2 i i1 i
i,2
100 1 1 1   1 1   1 1  1 1 1
∴
 











  
，选项C正确.
a 9 10 10 11 99 100 9 100 9
i10 i,2
∵i+ j =8,i³ j ，∴  a i,j a 4,4 a 5,3 a 6,2 a 7,1，
ij8
∵a a 23 4241619，a a 2252514 25，
4,4 4,1 5,3 5,1
a a 26261233，a 72 7143，
6,2 6,1 7,1
 a 19253343120
∴ i,j ，选项D正确.
ij8
故选：ACD.
【点睛】关键点点睛：解决本题的关键是观察得到所有等式等号右侧的项构成等差数列，根据等差数列的
通项公式计算a
n,1
和a
n,n
，由此分析a
n,2
和a
n,j
，从而确定正确选项.
三、填空题：本题共 3小题，每小题 5分，共 15分．
x2,x 1,
12. 已知函数 若 f  m1 1，则m的取值范围是______．
x1,x1,
【答案】
2,0 
【解析】
【分析】讨论m1的取值范围，解不等式可得结果.
【详解】当m11，即m0时，由 f  m1 1得 m1 2 1，解得2m0，
第10页/共22页
学科网（北京）股份有限公司当m11，即m0时，由 f  m1 1得m111，无解，
∴m的取值范围是 2,0  .
故答案为：
2,0 
.
13. 已知V ABC 满足tanA，tanB是方程x2 10x60的两个根，则cosC =______．
5
【答案】
5
【解析】
【分析】利用韦达定理、和角的正切公式及同角公式计算得解.
【详解】由tanA，tanB是方程x2 10x60的两个根，得tanAtanB 10,tanAtanB 6，
tan AtanB 10
在V ABC 中，tanC tan(AB)  20，C为锐角，
1tan AtanB 16
5
即sinC 2cosC，而sin2Ccos2C 1，所以cosC .
5
5
故答案为：
5
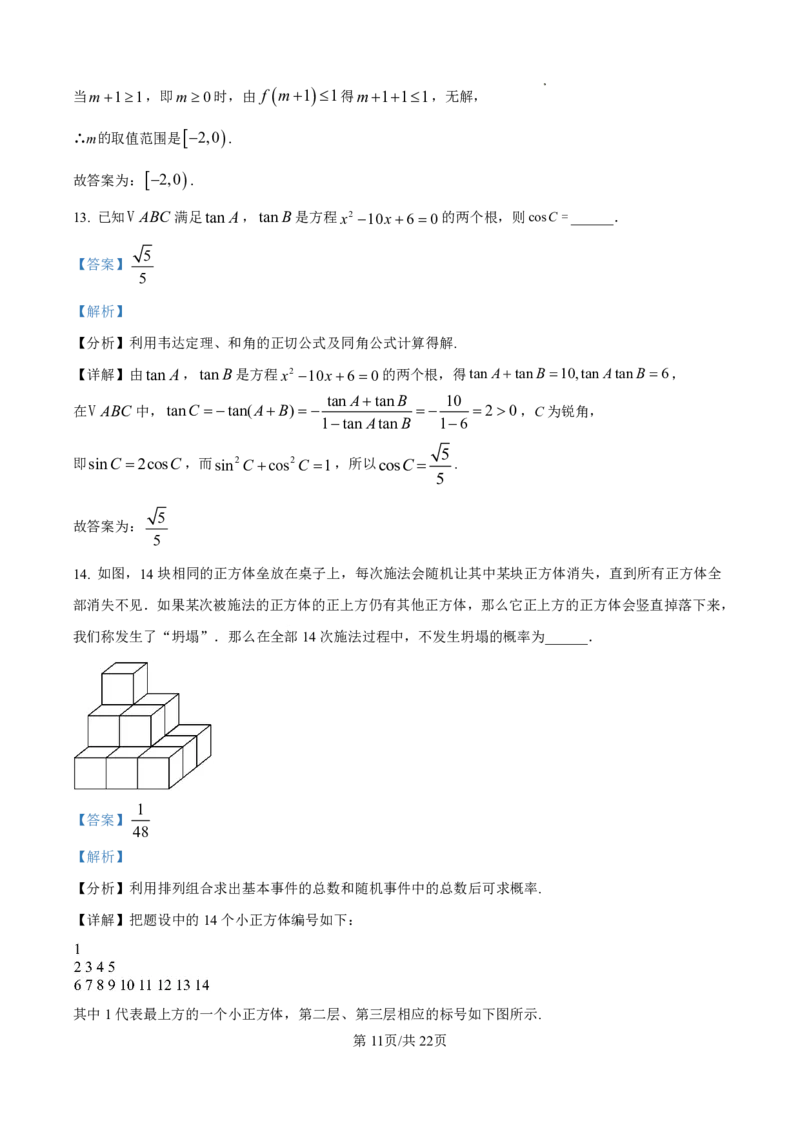
14. 如图，14块相同的正方体垒放在桌子上，每次施法会随机让其中某块正方体消失，直到所有正方体全
部消失不见．如果某次被施法的正方体的正上方仍有其他正方体，那么它正上方的正方体会竖直掉落下来，
我们称发生了“坍塌”．那么在全部14次施法过程中，不发生坍塌的概率为______．
1
【答案】
48
【解析】
【分析】利用排列组合求出基本事件的总数和随机事件中的总数后可求概率.
【详解】把题设中的14个小正方体编号如下：
其中1代表最上方的一个小正方体，第二层、第三层相应的标号如下图所示.
第11页/共22页
学科网（北京）股份有限公司与1号小正方体在同一个竖直方向小正方体从上至下记为2,6，
标号为3的正方体下面的小正方体标号为7，
标号为4的正方体下面的小正方体标号为8，
标号为5的正方体下面的小正方体标号为9，
若不发生坍塌，则
则全部14次施法过程中，不发生坍塌的事件总数为C3 C2C2C2A5
14 11 9 7 5
设事件A为：“全部14次施法过程中，不发生坍塌”，
C3 C2C2C2A5 1
则P  A  14 11 9 7 5 
A14 48
14
1
故答案为： .
48
【点睛】思路点睛：对于古典概型的概率计算问题，我们在计算事件总数时需借助排列组合的方法，对于
一些比较繁琐的计数问题，我们可以将问题模型化，从而便于计数.
四、解答题：本题共 5小题，共 77分．解答应写出文字说明、证明过程或演算步骤．
15. 已知数列{a }的前n项和为S ，S 2a 2．
n n n n
（1）求{a }的通项公式；
n
（2）在{a }相邻两项中间插入相邻两项的等差中项，求所得新数列{b }的前2n项和T ．
n n 2n
【答案】（1）a 2n
n
（2）T 52n 5
2n
【解析】
【分析】（1）由S 2a 2可得S 2a 2，两式相减，根据等比数列的定义，代入通项公式，即可
n n n1 n1
得答案.
a a
（2）设数列{c }满足c  n n1 32n1，记{c }的前n项和为R ，则T R S ，根据等比数列求
n n 2 n n 2n n n
第12页/共22页
学科网（北京）股份有限公司和公式，代入计算，即可得答案.
【小问1详解】
由S 2a 2可得S 2a 2．
n n n1 n1
两式相减并由a S S 得到a 2a ．
n1 n1 n n1 n
特别地，取n1，则由a S 知a 2．
1 1 1
所以{a }是以2为首项，公比为2的等比数列，
n
则a 22n1 2n．
n
所以{a }的通项公式是a 2n．
n n
【小问2详解】
a a
设数列{c }满足c  n n1 32n1．
n n 2
记{c }的前n项和为R ，则T R S ．
n n 2n n n
2(12n) 3(12n)
由等比数列的求和公式得：S   2(2n1)，R  3(2n1)．
n 12 n 12
所以T R S 52n5．
2n n n
即新数列{b }的前2n项和T 52n 5．
n 2n
ax
16. 已知函数 f  x ln  a0 是奇函数．
1ax
（1）求a；
（2）求曲线y  f  x  在点  0, f  0  处的切线方程；
（3）证明：函数g

x

f

x
2sinx有且仅有1个零点．
【答案】（1）a 1
（2）2x y 0
（3）证明见解析
【解析】
【分析】（1）根据奇函数定义得 f
x f 
x

，代入可求得a的值.
（2）求
f
x

，计算切线斜率即可得到切线方程.
第13页/共22页
学科网（北京）股份有限公司（3）求g
x

，分析函数g

x

的单调性即可确定证明结论.
【小问1详解】
ax
∵函数 f  x ln  a 0 是奇函数，
1ax
ax ax 1ax
∴ f x f  x  ，即ln ln ln ，
1ax 1ax ax
ax 1ax
 
∴  ，即 a2 1 x2 a2 10对定义域内任意x恒成立，
1ax ax
∴a2 1，解得a 1或1（舍），
1x
∴a 1，此时 f  x ln ，
1x
1x
由 0得 f  x  定义域为 1,1  ，符合题意.
1x
【小问2详解】
1x
由（1）得， f  x ln ln  1x ln  1x ，
1x
1 1
∴ f  0 0， f x   ，
1x 1x
∴ f 0 112，故曲线 y f  x  在点  0, f  0  处的切线方程为y 2x，即2x y 0.
【小问3详解】
∵g  x  f  x 2sinxln  1x ln  1x 2sinx，
1 1 2
∴函数g  x  的定义域为 1,1  ，g  0 0，g x   2cosx 2cosx，
1x 1x 1x2
2
∵1 x 1，∴01x2 1， 2，2cosx2，
1x2
2
∴g x  2cosx0，故g  x  在 1,1  上为增函数，
1x2
 
∴g x 有且仅有1个零点，零点为0.
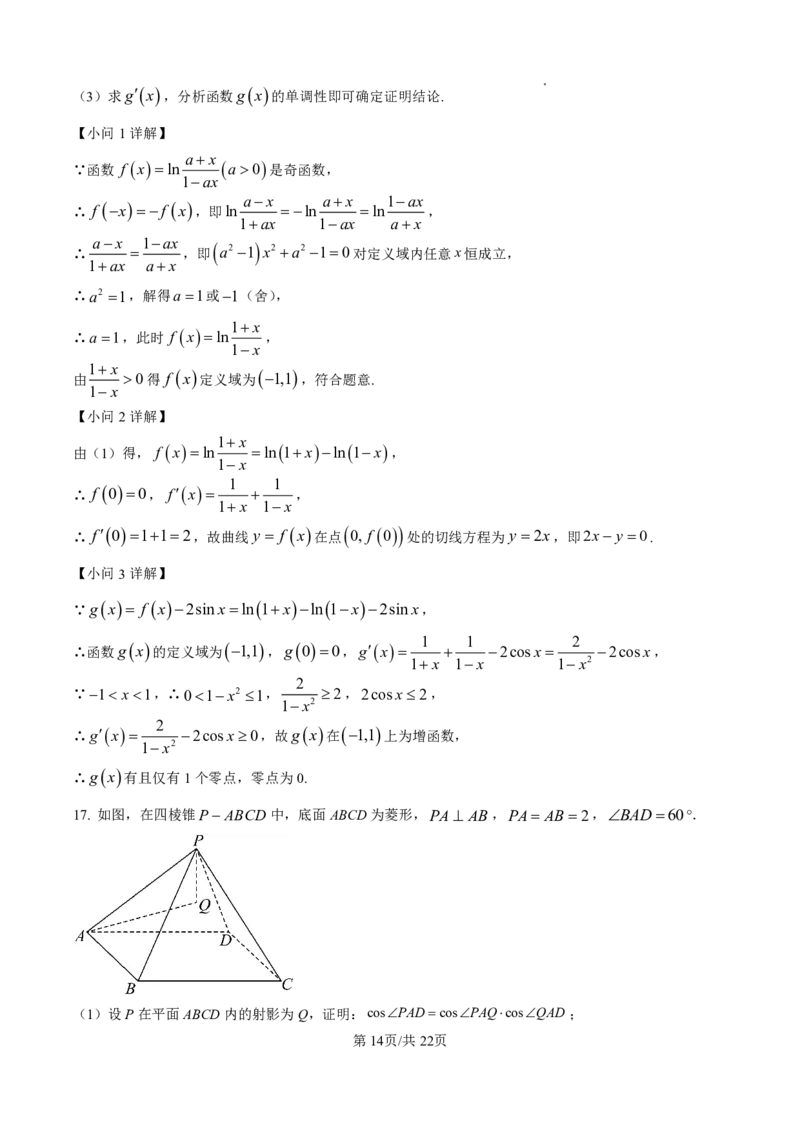
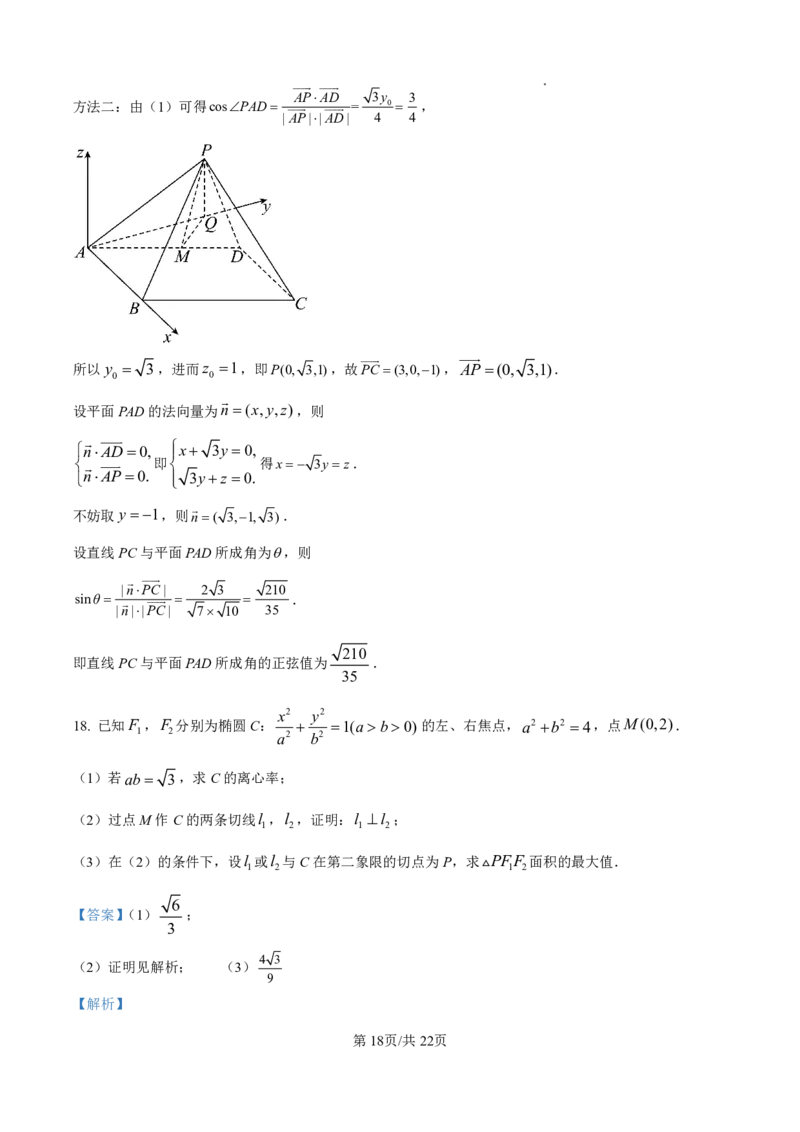
17. 如图，在四棱锥P ABCD中，底面ABCD为菱形，PA AB，PA AB  2，BAD60°．
（1）设P在平面ABCD内的射影为Q，证明：cosPADcosPAQcosQAD ；
第14页/共22页
学科网（北京）股份有限公司3
（2）若cosPAD ，求直线PC与平面PAD所成角的正弦值．
4
【答案】（1）证明见解析；
210
（2） .
35
【解析】
【分析】（1）作QM  AD于点M，结合条件可证AD 平面PQM，进而可得PM  AD，即证；或利
用坐标法；
（2）利用线面垂直的判断定理可得AB 平面PAQ，然后利用等积法可求C到平面平面PAD的距离，即
得；或利用坐标法.
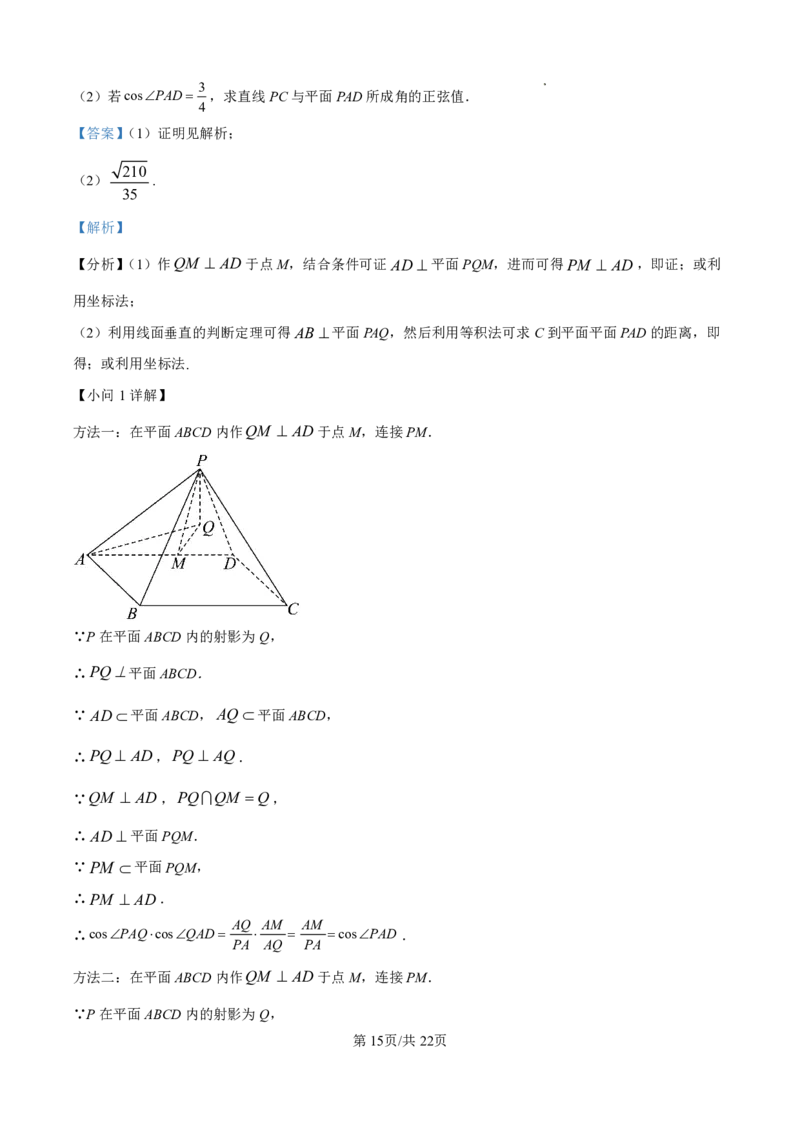
【小问1详解】
方法一：在平面ABCD内作QM  AD于点M，连接PM．
∵P在平面ABCD内的射影为Q，
∴PQ平面ABCD．
∵AD 平面ABCD，AQ平面ABCD，
∴PQ AD，PQ  AQ．
∵QM  AD，PQQM Q，
∴AD 平面PQM．
∵PM 平面PQM，
∴PM  AD．
AQ AM AM
∴cosPAQcosQAD   cosPAD ．
PA AQ PA
方法二：在平面ABCD内作QM  AD于点M，连接PM．
∵P在平面ABCD内的射影为Q，
第15页/共22页
学科网（北京）股份有限公司∴PQ平面ABCD．
∵AB平面ABCD，
∴PQAB．
∵PA AB，PQPA P，
∴AB 平面PAQ．
同理可得AQ AB，所以AB，AQ，PQ两两垂直．
  
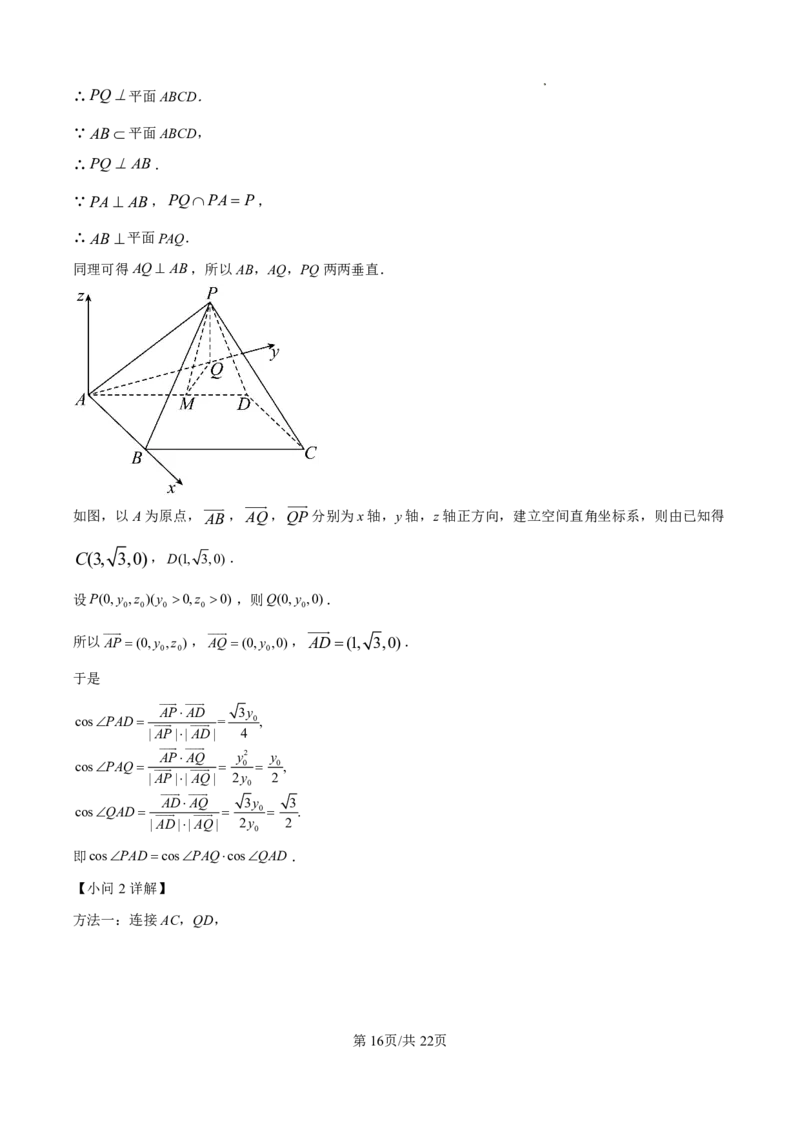
如图，以A为原点，AB，AQ，QP分别为x轴，y轴，z轴正方向，建立空间直角坐标系，则由已知得
C(3, 3,0)，D(1, 3,0)．
设P(0,y ,z )(y 0,z 0) ，则Q(0,y ,0)．
0 0 0 0 0
  
所以AP(0,y ,z )，AQ(0,y ,0)，AD(1, 3,0)．
0 0 0
于是
 
APAD 3y
cosPAD   = 0,
|AP||AD| 4
 
APAQ y2 y
cosPAQ    0  0,
|AP||AQ| 2y 2
0
 
ADAQ 3y 3
cosQAD    0  .
|AD||AQ| 2y 2
0
即cosPADcosPAQcosQAD．
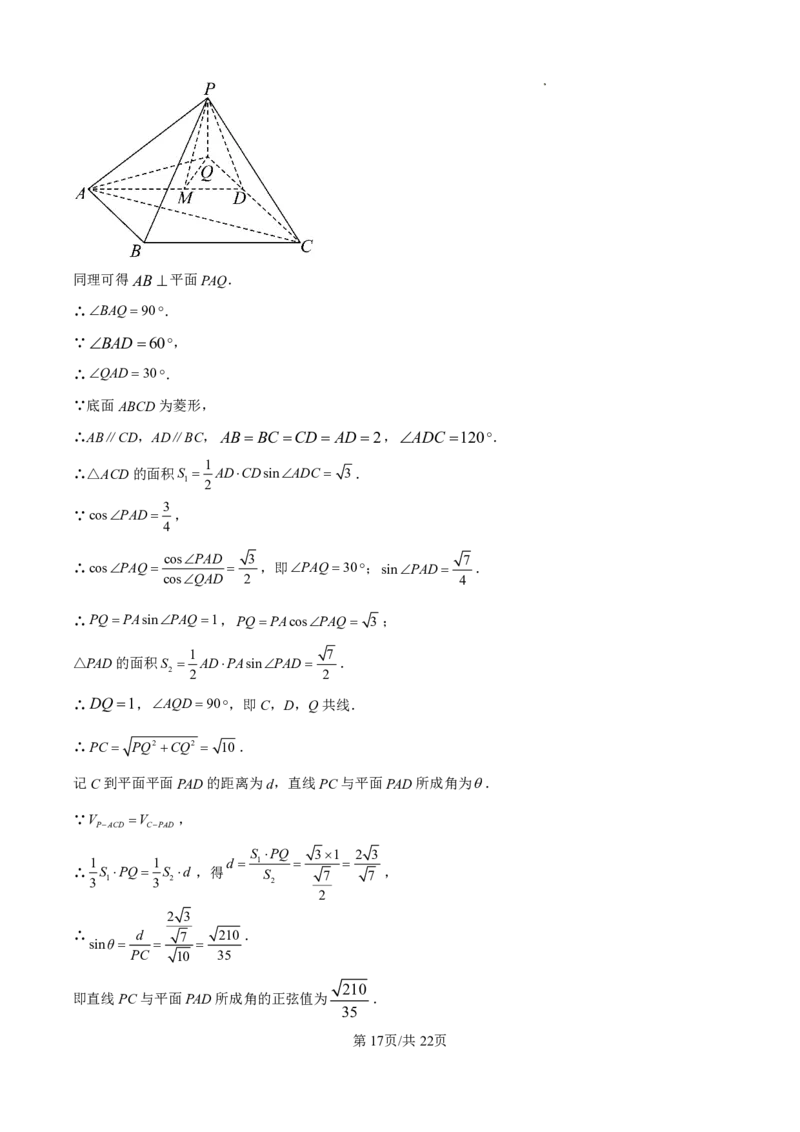
【小问2详解】
方法一：连接AC，QD，
第16页/共22页
学科网（北京）股份有限公司同理可得AB 平面PAQ．
∴BAQ90°．
∵BAD60°，
∴QAD30°．
∵底面ABCD为菱形，
∴AB∥CD，AD∥BC，ABBC CD AD2，ADC 120°．
1
∴△ACD的面积S  ADCDsinADC  3．
1 2
3
∵cosPAD ，
4
cosPAD 3 7
∴cosPAQ  ，即PAQ30°；sinPAD ．
cosQAD 2 4
∴PQPAsinPAQ1，PQPAcosPAQ 3 ；
1 7
△PAD的面积S  ADPAsinPAD ．
2 2 2
∴DQ1，AQD90°，即C，D，Q共线．
∴PC  PQ2 CQ2  10．
记C到平面平面PAD的距离为d，直线PC与平面PAD所成角为．
∵V V ，
PACD CPAD
S PQ 31 2 3
1 1 d  1  
∴ 3 S 1 PQ 3 S 2 d ，得 S 2 7 7 ，
2
2 3
∴ d 7 210 ．
sinθ   
PC 10 35
210
即直线PC与平面PAD所成角的正弦值为 ．
35
第17页/共22页
学科网（北京）股份有限公司 
APAD 3y 3
方法二：由（1）可得cosPAD   = 0  ，
|AP||AD| 4 4
 
所以 y  3，进而z 1，即P(0, 3,1)，故PC (3,0,1)，AP(0, 3,1)．
0 0

设平面PAD的法向量为n (x,y,z)，则
n    A  D  0,  x 3y 0,
  即 得x 3yz．
nAP0.  3yz 0.
不妨取 y 1，则n  ( 3,1, 3)．
设直线PC与平面PAD所成角为，则
 
|nPC| 2 3 210
sinθ      ．
|n||PC| 7 10 35
210
即直线PC与平面PAD所成角的正弦值为 ．
35
x2 y2
18. 已知F ，F 分别为椭圆C：  1(ab0)的左、右焦点，a2 b2 4，点M(0,2)．
1 2 a2 b2
（1）若ab 3，求C的离心率；
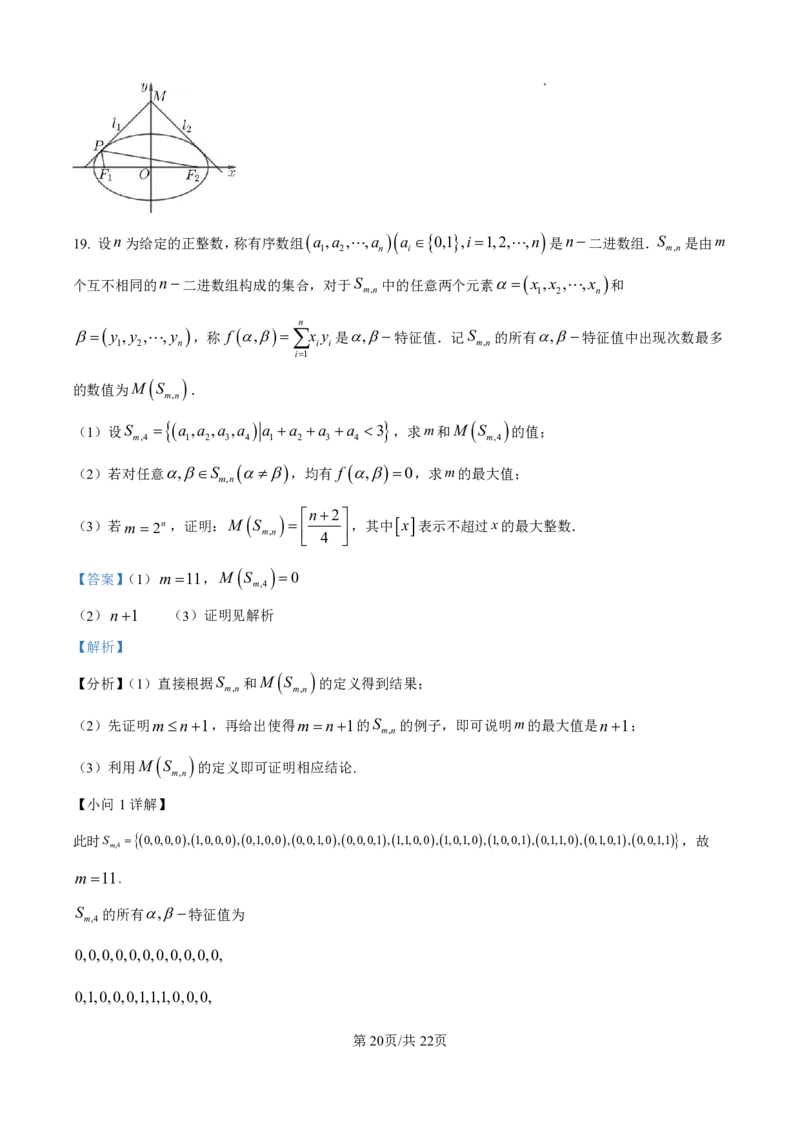
（2）过点M作C的两条切线l ，l ，证明：l l ；
1 2 1 2
（3）在（2）的条件下，设l 或l 与C在第二象限的切点为P，求PFF 面积的最大值．
1 2 1 2
6
【答案】（1） ；
3
4 3
（2）证明见解析； （3）
9
【解析】
第18页/共22页
学科网（北京）股份有限公司【分析】（1）根据给定条件，求出a,b，进而求出离心率.
（2）设出切线方程，与椭圆方程联立，利用判别式为0求出切线斜率即可得证.
（3）设切点P(x ,y )，由（2）可得a2 2x ,2 x 1，再利用x 表示出三角形面积，进而求出最
0 0 0 0 0
大值.
【小问1详解】
 a2 b2 4
由 及a b0，得a  3,b1，
ab 3
a2 b2 2 6
所以椭圆C的离心率e   .
a 3 3
【小问2详解】
设过点M 的椭圆C的切线方程为 y  kx2，
y kx2
由 消去y得(a2k2 b2)x2 4a2kxa2(4b2)0 ，
b2x2 a2y2 a2b2
则16a4k24a4(a2k2b2)0 ，整理得(4a2)k2 b2，即b2k2 b2，解得k 1，
不妨令直线l 的斜率为1，则直线l 的斜率为1，1(1)1，
1 2
所以l l .
1 2
【小问3详解】
由（2）知，切线方程为 y  x2，设切点P(x ,y )，
0 0
则 y  x 2，且4x2 4a2x a4 0，即 y  x 2且a2 2x ，
0 0 0 0 0 0 0
由a b0，得a2 4a2，则2a2 4，即22x 4，解得2 x 1，
0 0
|FF |2 a2b2 2 2a24 2 4x 4 4 x 1 ，令x 1t(0,1)，
1 2 0 0 0
1
因此PFF 的面积S  | y ||FF |2(1t) t  2 (1t)22t
1 2 PF 1 F 2 2 0 1 2
1t1t2t 4 3 1 4
 2 ( )3  ，当且仅当1t 2t，即t  ,x  时取等号，
3 9 3 0 3
4 3
所以PFF 的面积为 .
1 2
9
第19页/共22页
学科网（北京）股份有限公司19. 设n为给定的正整数，称有序数组  a ,a ,,a  a  0,1  ,i 1,2,,n  是n二进数组．S 是由m
1 2 n i m,n
个互不相同的n二进数组构成的集合，对于S 中的任意两个元素 x ,x ,,x  和
m,n 1 2 n
n
 y ,y ,,y  ，称 f ,x y 是,特征值．记S 的所有,特征值中出现次数最多
1 2 n i i m,n
i1
 
的数值为M S ．
m,n
（1）设S   a ,a ,a ,a  a a a a 3  ，求m和M  S  的值；
m,4 1 2 3 4 1 2 3 4 m,4
（2）若对任意,S  ，均有 f ,0，求m的最大值；
m,n
n2
（3）若m  2n，证明：M  S m,n     4   ，其中  x  表示不超过x的最大整数．
 
【答案】（1）m11，M S 0
m,4
（2）n1 （3）证明见解析
【解析】
 
【分析】（1）直接根据S 和M S 的定义得到结果；
m,n m,n
（2）先证明mn1，再给出使得mn1的S 的例子，即可说明m的最大值是n1；
m,n
 
（3）利用M S 的定义即可证明相应结论.
m,n
【小问1详解】
此时S 0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,0,0,0,0,1,1,1,0,0,1,0,1,0,1,0,0,1,0,1,1,0,0,1,0,1,0,0,1,1，故
m,4
m11.
S 的所有,特征值为
m,4
0,0,0,0,0,0,0,0,0,0,0,
0,1,0,0,0,1,1,1,0,0,0,
第20页/共22页
学科网（北京）股份有限公司0,0,1,0,0,1,0,0,1,1,0,
0,0,0,1,0,0,1,0,1,0,1,
0,0,0,0,1,0,0,1,0,1,1,
0,1,1,0,0,2,1,1,1,1,0,
0,1,0,1,0,1,2,1,1,0,1,
0,1,0,0,1,1,1,2,0,1,1,
0,0,1,1,0,1,1,0,2,1,1,
0,0,1,0,1,1,0,1,1,2,1,
0,0,0,1,1,0,1,1,1,1,2.
 
以上共121个，其中有63个0，52个1，6个2，所以M S 0.
m,4
【小问2详解】
由于对任意k 1,2,...,n，S 不能出现两个第k位为1的数组,（否则 ）.
m,n
,  >0
所以S 中每个数组包含1的数目之和不超过n.
m,n
由于不包含1的数组至多有一个  0,0,0,...,0,0  ，故S 中至少有m1个包含至少一个1的数组.
m,n
所以S 中每个数组包含1的数目之和不小于m1.
m,n
以上二者结合，即可得到nm1，故mn1.
当S   a ,a ,a ,...,a  a a a ...a 1  时，对任意S 中的两个不同元素,，均有
m,n 1 2 3 n 1 2 3 n m,n
f
,0.
所以m的最大值是n1.
【小问3详解】
由于所有的n二进数组恰有2n个，故S 必定是包含全部n二进数组的集合.
m,n
对l 0,1,2,...,n  ，设T  l  为使得 f ,l的有序对 , 的数量，其中,S .
m,n
n!
那么在这种情况下，,的同为1的那l个分量位置有Cl
n

l!  nl  !
种选择.
第21页/共22页
学科网（北京）股份有限公司确定这些位置后，其它的分量不能同为1，那么每个位置有三种可能，所以剩余分量有3nl种选择.
3nl·n! T  l1  nl
这就得到T  l  ，从而  .
l!  nl  ! T  l  3  l1 
n3
n3 T  l1  nl n 4
故当l  时，有 ；当 时，有   1 .
4   +1  −    − −  3 − 4 3  −3 T  l  3  l 1  3   n3 1  
=3  +1 >3 4 +1 =1  > 4  4 
n3 n2
从而当l取到大于 的最小整数，也就是l 
 
时，T  l  取得最大值.
4  4 
n2
 
所以M S m,n    4   .
【点睛】关键点点睛：本题的关键在于对集合S 的定义的理解。只有理解了定义，方可解决相应问题.
m,n
第22页/共22页
学科网（北京）股份有限公司