文档内容
模块过关卷(四)
统计思想与方法
一、填一填。(第2、3、4、10题每题2分,第5题7分,其余每题3
分,共30分)
1.扇形统计图可以清楚地表示出( )和( )之间的关
系;( )统计图不但可以表示出数量的多少,而且可以清楚
地表示出数量增减变化的情况。
2.一个盒子里有8个红球,4个蓝球,2个白球,
它们的大小、形状一样,从中任意摸一个球,
摸到( )球的可能性最大,摸到( )球的
可能性最小。
3.右图是六(1)班图书角图书情况统计图。
(1)童话书占图书总数的( )%。
(2)如果科技书有150本,那么作文书有( )本。
4.在一个条形统计图里,若用1.5厘米高的直条表示10吨,则用(
)厘米高的直条表示40吨,用9厘米高的直条表示( )吨。5.口袋里有9张数字卡片,从中任意摸出1张。
(1)( )摸到自然数,( )摸到小数。(填“一定”“可能”或
“不可能”)
(2)摸到( )的可能性大,摸到( )的可能性小。(填“奇数”或
“偶数”)
(3)摸到( )、( )和( )的可能性相等。(填“奇数”
“偶数”“质数”或“合数”)
6.亮亮前几次英语测试的平均成绩为84分,这次测试要得100分,
才能把这几次英语测试的平均成绩提到86分,这是第( )次测试。
7.在学校组织的校园舞比赛中,七位评委老师给六(2)班的评分分别
是(单位:分):9.45、9.47、9.38、9.55、9.24、9.35、9.40。去掉
一个最高分和一个最低分,六(2)班最终平均得分是( )分。
8.有三张数字卡片,,,任意选两个组成两位数,两位数是奇数的
小芳赢,两位数是偶数的小玲赢,她们两人中( )赢的可能性
大。9.要统计学校各社团人数,应绘制( )统计图;要统计午餐各
种营养成分所占的百分比,应绘制( )统计图;要统计文文
6~12岁体重变化情况,应绘制( )统计图。
10.跳绳比赛前,采用“石头”“剪刀”“布”的游戏方法确定谁先
跳,这种游戏规则是( )的。(填“公平”或“不公平”)
二、辨一辨。(对的在括号里画“√”,错的画“×”。每题2分,共
10分)
1.王强所在班的平均身高大于李亮所在班的平均身高,那么王强一
定比李亮高。 ( )
2.一次抽奖的中奖率是10%,抽100次一定有10次中奖。 ( )
3.抛硬币时正面向上和反面向上的可能性是相等的,明明抛了20次,
肯定有10次正面向上。 ( )
4.赵彤把妈妈手机号码的最后一个数字忘了,她随意拨了一个数字,
不可能拨对。 ( )
5.盒子里放有两种不同颜色的球,小刚摸了10次,其中5次摸到黑
球,5次摸到白球,说明这两种球一样多。 ( )三、选一选。(把正确答案的序号填在括号里。每题2分,共10分)
1.心脏科要把病人的血压变化情况绘制成统计图,最佳选择是( )。
A.条形统计图 B.折线统计图
C.扇形统计图 D.三类统计图都可以
2.某地天气预报中说:“明天降雨的概率为95%”,也就是说( )。
A.明天95%的地区下雨 B.明天下雨的可能性很大
C.明天下雨的可能性很小 D.明天一定会下雨
3.甲、乙两个数的平均数是16,乙、丙两个数的平均数是14,则甲
比丙( )。
A.少4 B.多4 C.少2 D.多2
4.骰子的六个面上分别刻有1到6个点,同时抛掷两枚骰子,下列说
法中不可能实现的是( )。
A.点数之和是12 B.点数之和小于3
C.点数之和是13 D.点数之和是7
5.盒子里有8个球,上面分别标有2,3,4,5,6,7,8,9八个数,
这些球除标的数不同外其他都相同,甲、乙二人玩摸球游戏,下
面规则中对双方公平的是( )。A.任意摸一球,摸到质数甲胜,摸到合数乙胜
B.任意摸一球,摸到的数小于5甲胜,摸到的数大于5乙胜
C.任意摸一球,摸到2的倍数甲胜,摸到5的倍数乙胜
D.任意摸一球,摸到奇数甲胜,摸到4的倍数乙胜
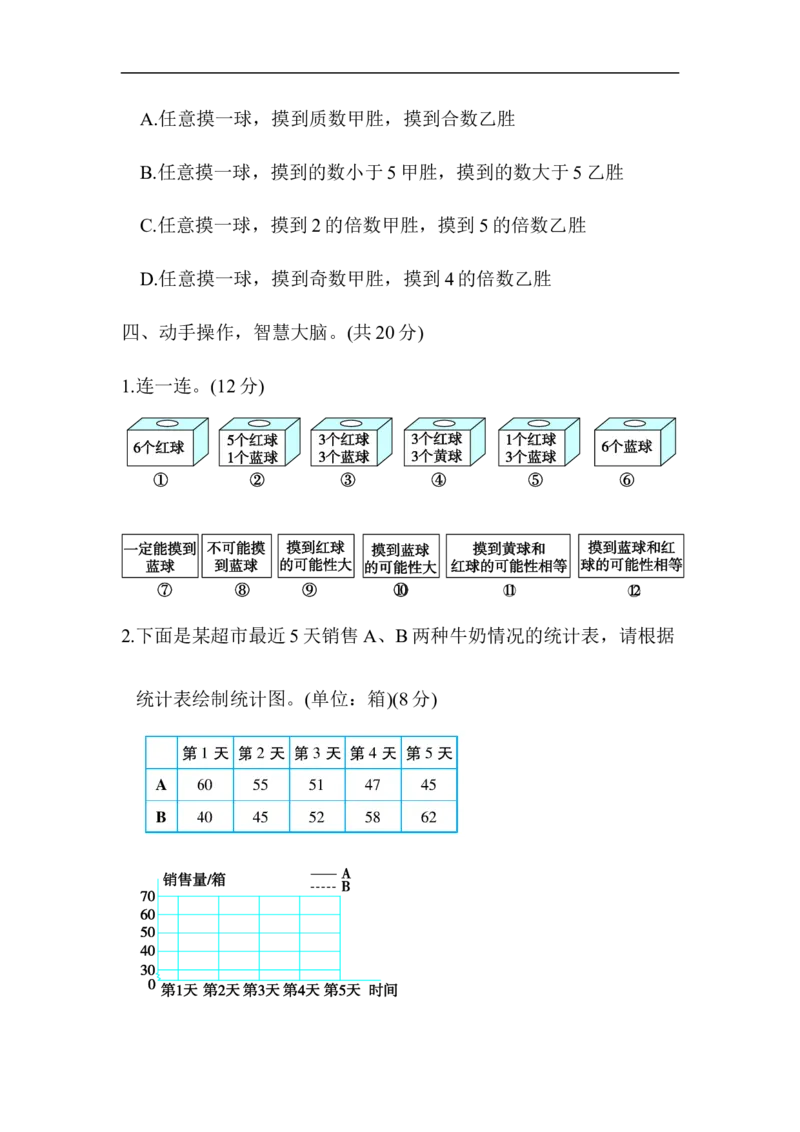
四、动手操作,智慧大脑。(共20分)
1.连一连。(12分)
2.下面是某超市最近5天销售A、B两种牛奶情况的统计表,请根据
统计表绘制统计图。(单位:箱)(8分)五、走进生活,解决问题。(共30分)
1.每年的6月5日是“世界环境日”,为配合今年的“世界环境
日”宣传活动,某校课外活动小组对全校师生开展了以“爱护环
境,从我做起”为主题的问卷调查活动,将调查结果分析整理后,
制成了下面两个统计图。
A.能将垃圾放到规定的地方,而且还会考虑垃圾的分类。
B.能将垃圾放到规定的地方,但不会考虑垃圾的分类。
C.偶尔会将垃圾放到规定的地方。
D.随手乱扔垃圾。
根据以上信息,回答下列问题。
(1)该校课外活动小组调查了多少人?并补全条形统计图。(3分)
(2)如果该校共有师生2600人,那么随手乱扔垃圾的约有多少人?(3
分)2.萌萌和萍萍一起玩游戏,规则是:将,,,,这5张卡片洗匀反
扣在桌面上,一人随机抽一张,若两人抽取的卡片上的数字之和
大于10则萌萌胜,小于10则萍萍胜,等于10则重新抽取。你认
为这个游戏公平吗?请说明理由。(6分)
3.甲、乙两人用同样多的钱一起买了22瓶葡萄酒,甲拿了12瓶,
乙拿了10瓶,后来甲又补给乙26元钱。请问:每瓶葡萄酒多少
钱?(5分)
4.有甲、乙、丙、丁四个数,每次去掉一个数,求其余三个数的平
均数,这样得到以下4个数:45,60,65,70,求甲、乙、丙、丁四个数的平均数。(5分)
5.在底面积为100平方厘米,高为20厘米的长方体水槽内放入一
个圆柱形烧杯,以恒定不变的速度先向圆柱形烧杯内注水,注满
烧杯后,继续注水,直到注满水槽为止。在此过程中,烧杯本身
的质量,体积忽略不计,烧杯在水槽中的位置始终不变,水槽中
水面上升的高度h(厘米)与注水时间t(秒)的关系如图所示。
(1)图中点( )表示烧杯中刚好注满水,点( )表示水槽中水面正
好与烧杯中水面齐平。(2分)
(2)求烧杯的底面积。(3分)(3)求注水的速度与水槽注满水所用的时间。(3分)答案
一、1.各部分量 总量 折线 2.红 白
3.(1)40 (2)60 4.6 60
5.(1)一定 不可能 (2) 奇数 偶数
(3)偶数 质数 合数
6.8 7.9.41 8.小玲
9.条形 扇形 折线 10.公平
二、1.× 2.× 3.× 4.× 5.×
三、1.B 2.B 3.B 4.C 5.A
四、1.
2.
五、1.(1)150÷50%=300(人)
答:该校课外活动小组调查了300人。
D类人数:300-150-30-90=30(人)(2)2600×=260(人)
答:随手乱扔垃圾的约有260人。
2.3+4=7 3+5=8 3+6=9 3+7=10 4+5=9
4+6=10 4+7=11 5+6=11 5+7=12 6+7=13
答:公平,因为和大于10的有4种,小于10的也有4种,获胜
可能性一样大。
3.26÷(22÷2-10)=26(元)
答:每瓶葡萄酒26元。
4.(45×3+60×3+65×3+70×3)÷3÷4=60
答:甲、乙、丙、丁四个数的平均数是60。
5.(1)A B
(2)解:设烧杯的底面积为x平方厘米。
=
(90-18)x=18(100-x)
72x=1800-18x90x=1800
x=20
答:烧杯的底面积为20平方厘米。
(3)20×10÷18=(立方厘米/秒)
100×20÷=180(秒)
答:注水的速度为立方厘米/秒,水槽注满水所用的时间为
180秒。