文档内容
2021年湖南省郴州市中考数学试卷
一、选择题(共8小题,每小题3分,共24分)
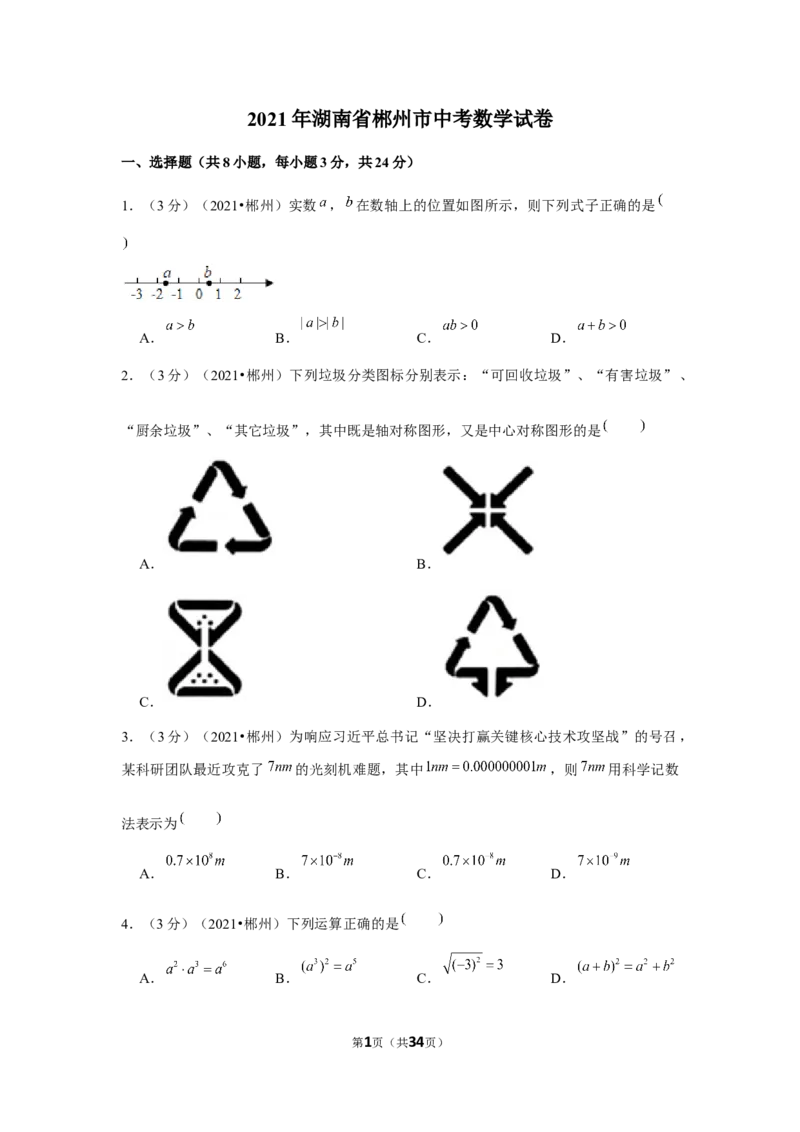
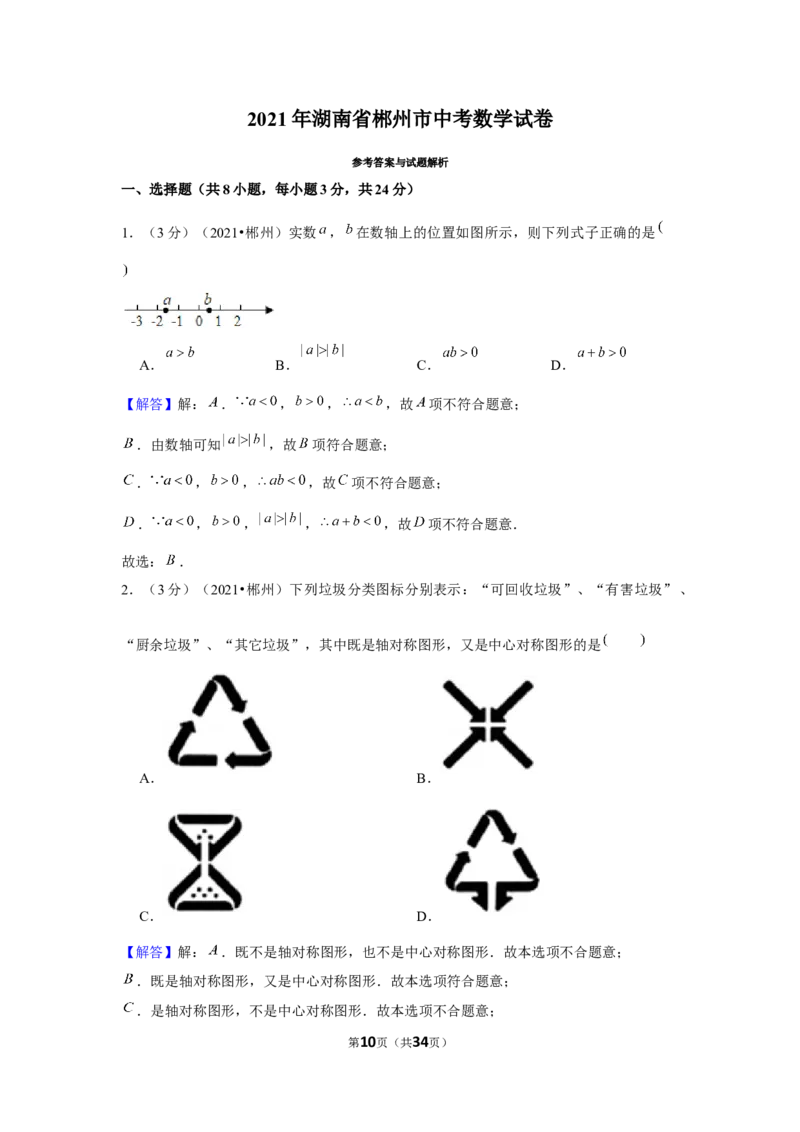
1.(3分)(2021•郴州)实数 , 在数轴上的位置如图所示,则下列式子正确的是
A. B. C. D.
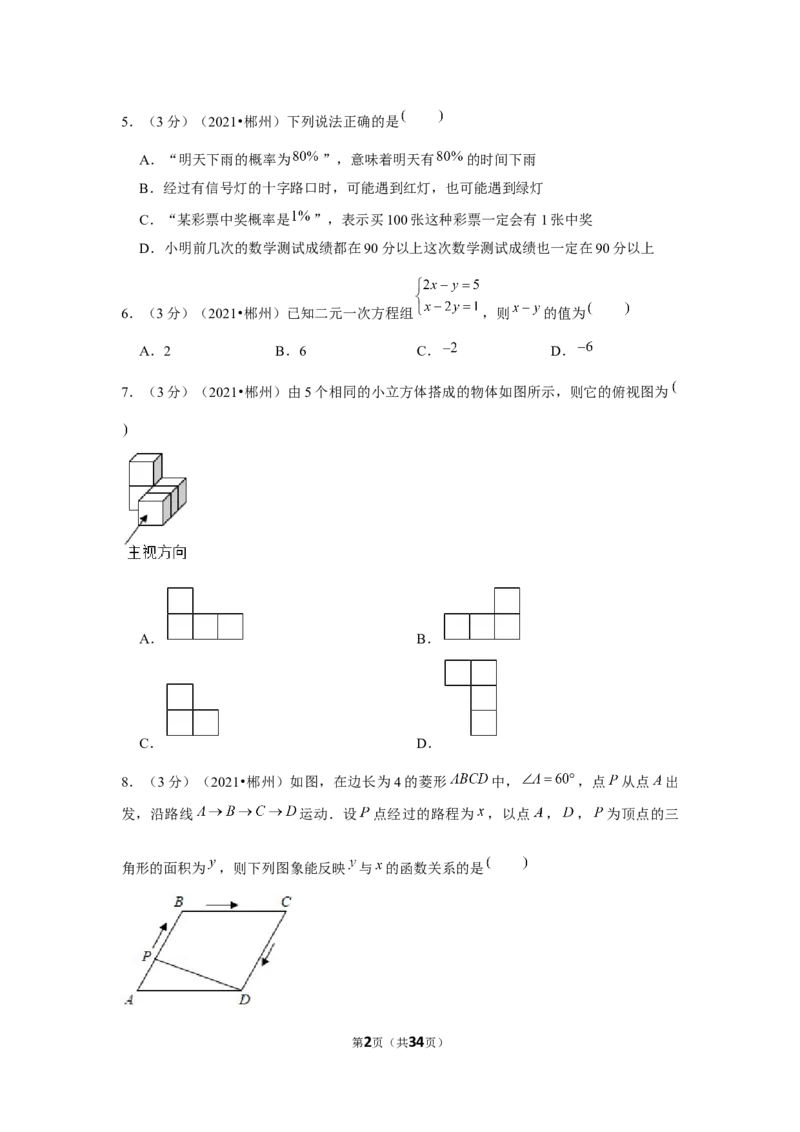
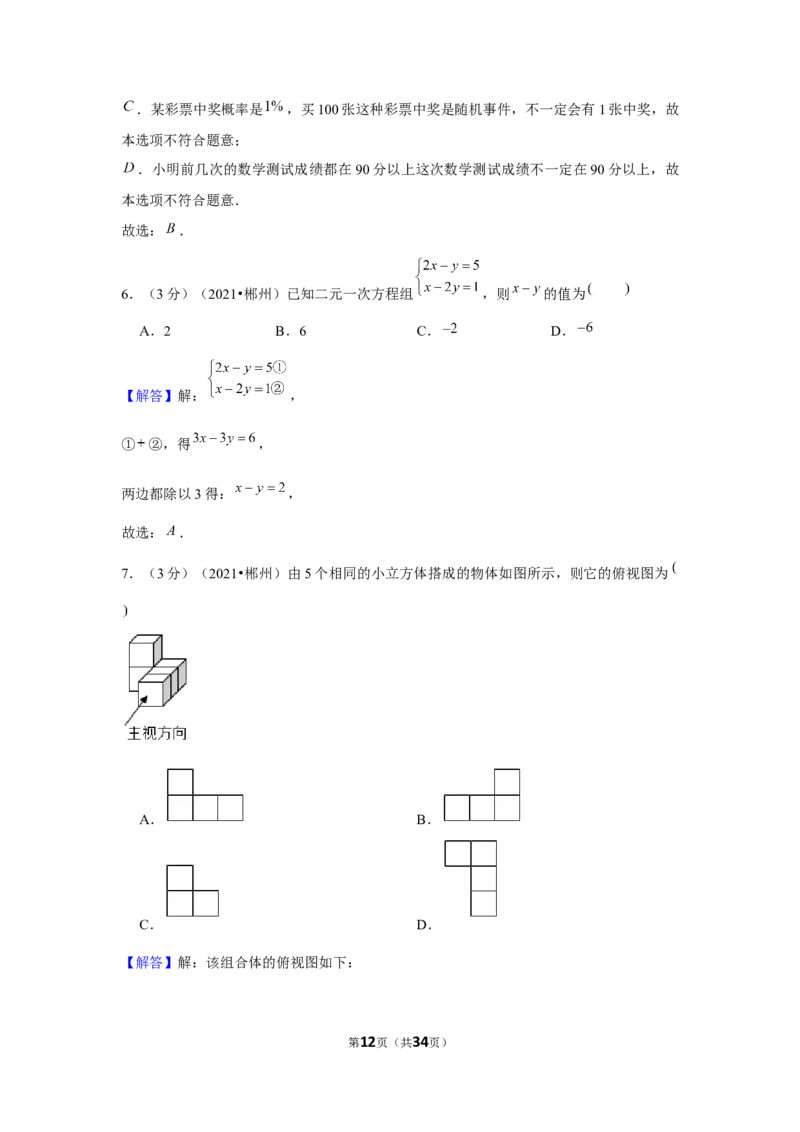
2.(3分)(2021•郴州)下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、
“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是
A. B.
C. D.
3.(3分)(2021•郴州)为响应习近平总书记“坚决打赢关键核心技术攻坚战”的号召,
某科研团队最近攻克了 的光刻机难题,其中 ,则 用科学记数
法表示为
A. B. C. D.
4.(3分)(2021•郴州)下列运算正确的是
A. B. C. D.
第1页(共34页)5.(3分)(2021•郴州)下列说法正确的是
A.“明天下雨的概率为 ”,意味着明天有 的时间下雨
B.经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯
C.“某彩票中奖概率是 ”,表示买100张这种彩票一定会有1张中奖
D.小明前几次的数学测试成绩都在90分以上这次数学测试成绩也一定在90分以上
6.(3分)(2021•郴州)已知二元一次方程组 ,则 的值为
A.2 B.6 C. D.
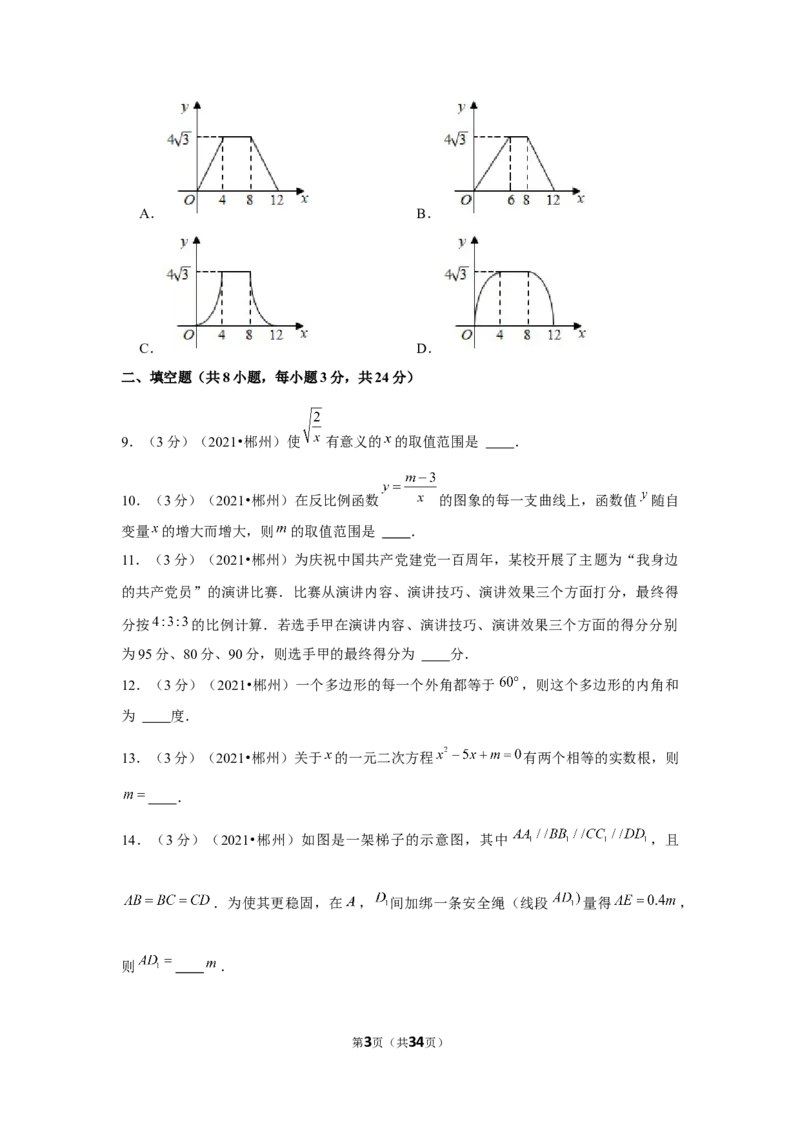
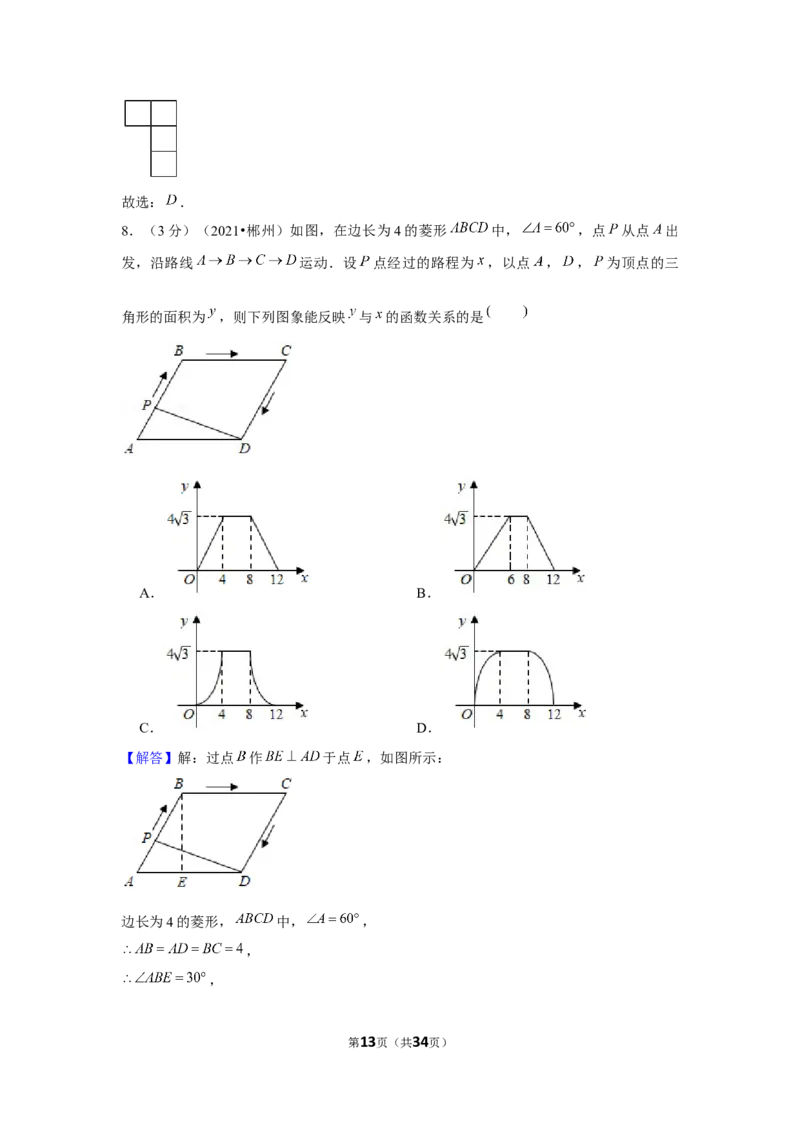
7.(3分)(2021•郴州)由5个相同的小立方体搭成的物体如图所示,则它的俯视图为
A. B.
C. D.
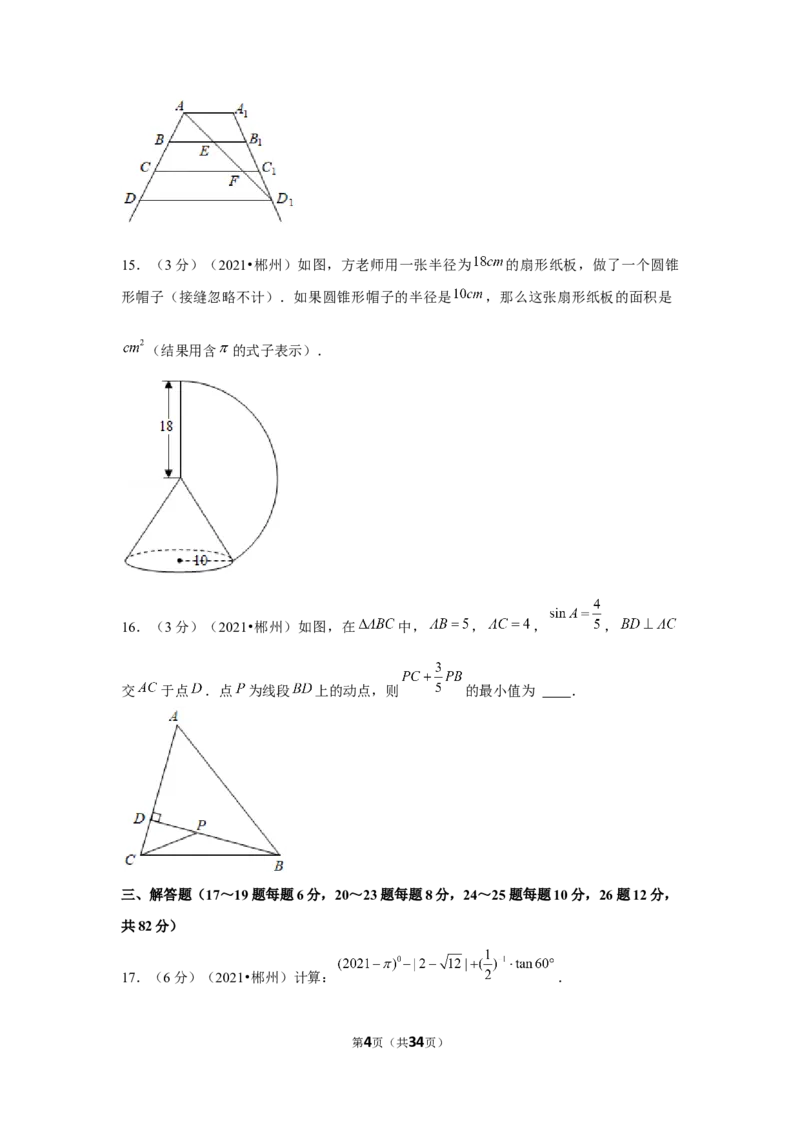
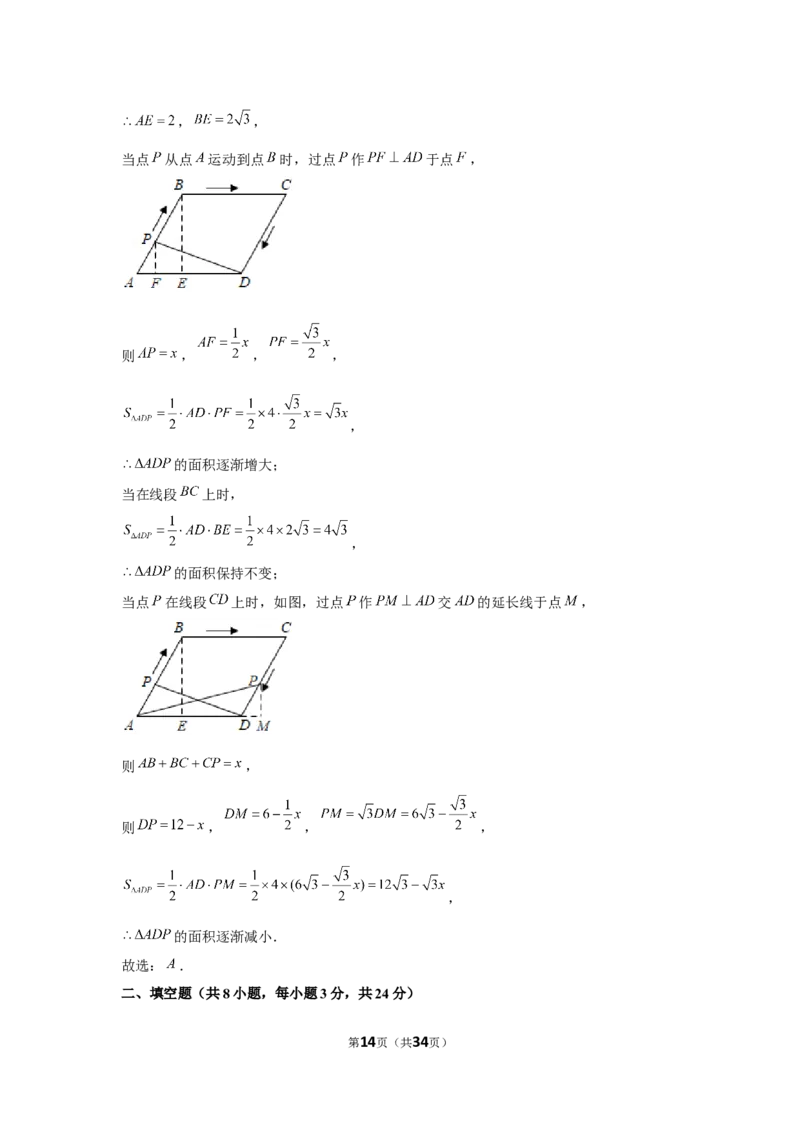
8.(3分)(2021•郴州)如图,在边长为4的菱形 中, ,点 从点 出
发,沿路线 运动.设 点经过的路程为 ,以点 , , 为顶点的三
角形的面积为 ,则下列图象能反映 与 的函数关系的是
第2页(共34页)A. B.
C. D.
二、填空题(共8小题,每小题3分,共24分)
9.(3分)(2021•郴州)使 有意义的 的取值范围是 .
10.(3分)(2021•郴州)在反比例函数 的图象的每一支曲线上,函数值 随自
变量 的增大而增大,则 的取值范围是 .
11.(3分)(2021•郴州)为庆祝中国共产党建党一百周年,某校开展了主题为“我身边
的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得
分按 的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别
为95分、80分、90分,则选手甲的最终得分为 分.
12.(3分)(2021•郴州)一个多边形的每一个外角都等于 ,则这个多边形的内角和
为 度.
13.(3分)(2021•郴州)关于 的一元二次方程 有两个相等的实数根,则
.
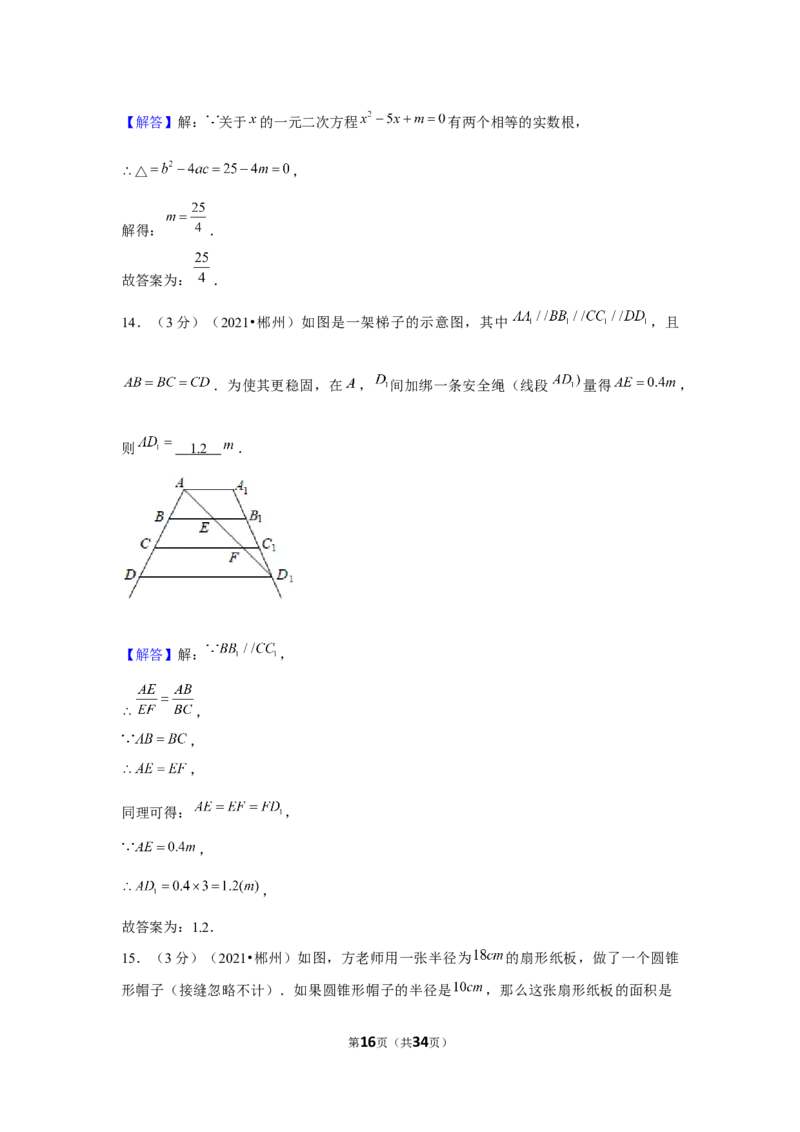
14.(3分)(2021•郴州)如图是一架梯子的示意图,其中 ,且
.为使其更稳固,在 , 间加绑一条安全绳(线段 量得 ,
则 .
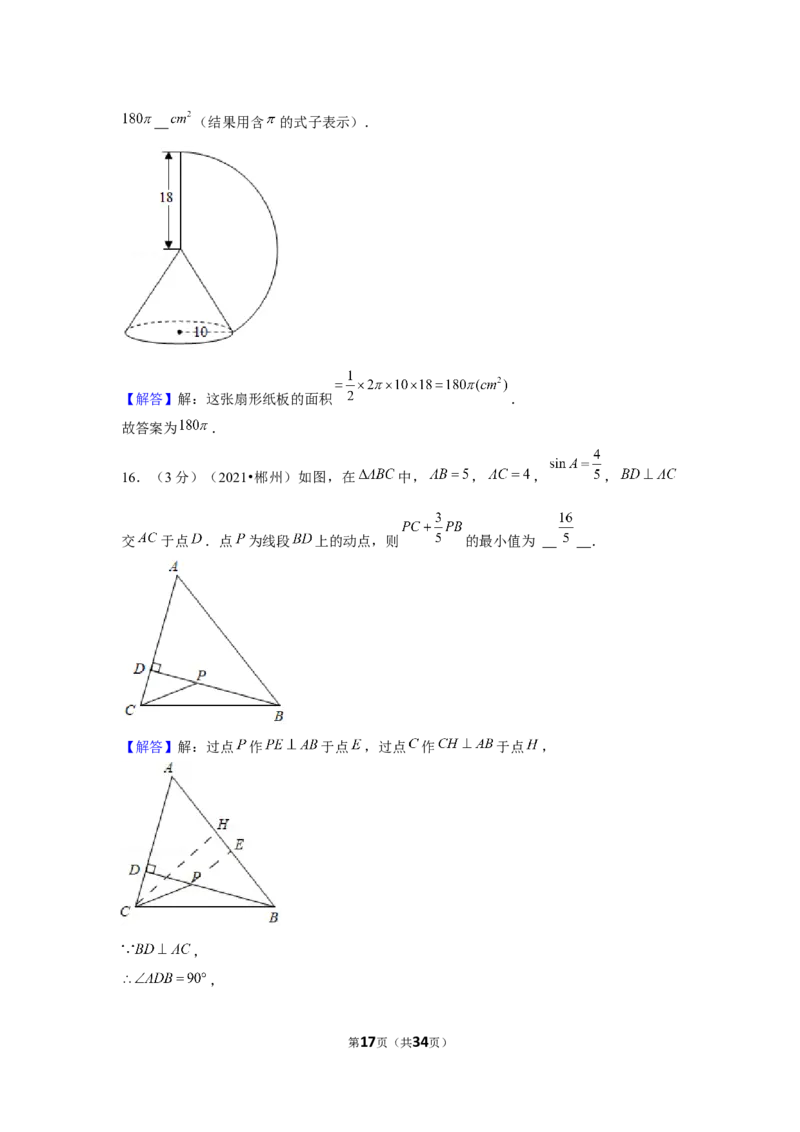
第3页(共34页)15.(3分)(2021•郴州)如图,方老师用一张半径为 的扇形纸板,做了一个圆锥
形帽子(接缝忽略不计).如果圆锥形帽子的半径是 ,那么这张扇形纸板的面积是
(结果用含 的式子表示).
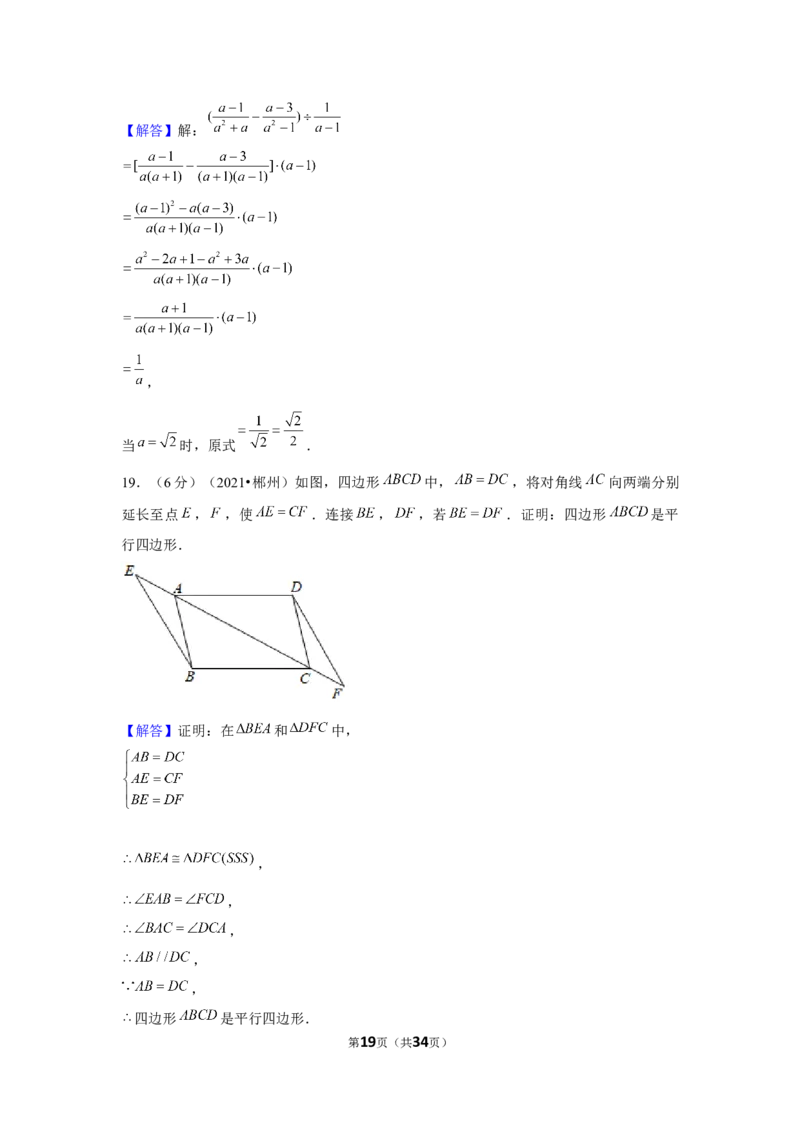
16.(3分)(2021•郴州)如图,在 中, , , ,
交 于点 .点 为线段 上的动点,则 的最小值为 .
三、解答题(17~19题每题6分,20~23题每题8分,24~25题每题10分,26题12分,
共82分)
17.(6分)(2021•郴州)计算: .
第4页(共34页)18.(6分)(2021•郴州)先化简,再求值: ,其中 .
19.(6分)(2021•郴州)如图,四边形 中, ,将对角线 向两端分别
延长至点 , ,使 .连接 , ,若 .证明:四边形 是平
行四边形.
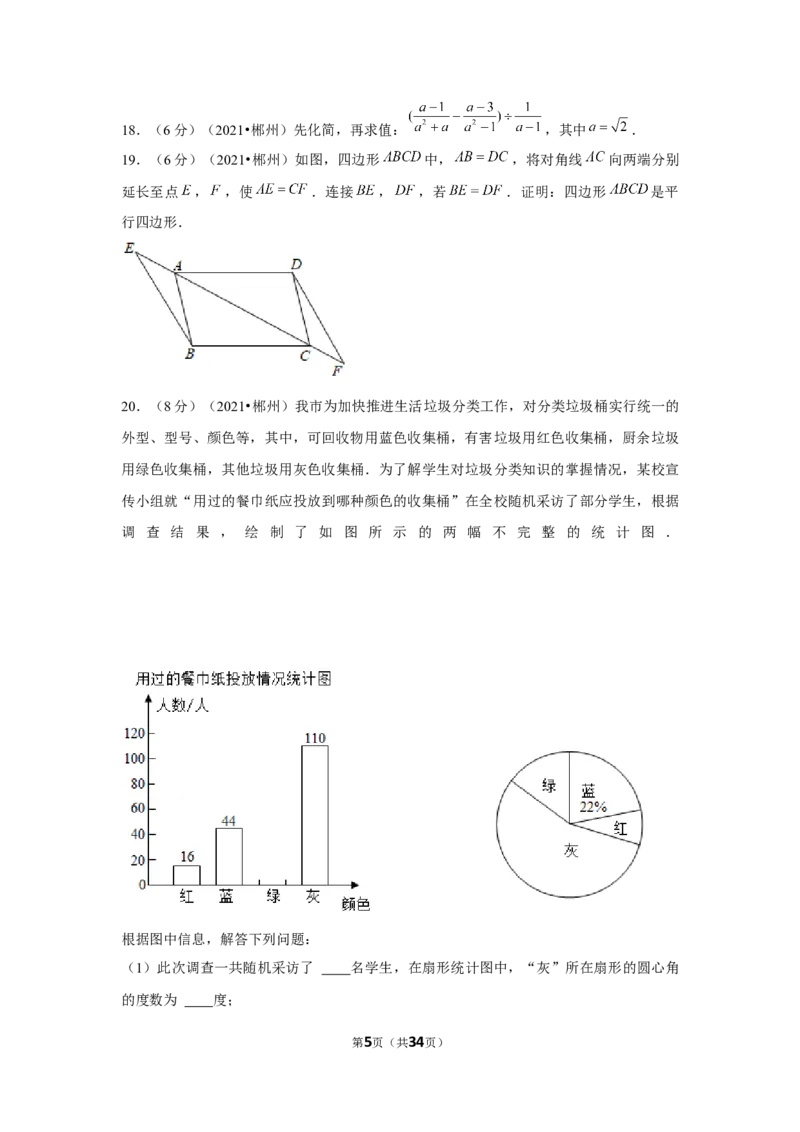
20.(8分)(2021•郴州)我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的
外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾
用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣
传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据
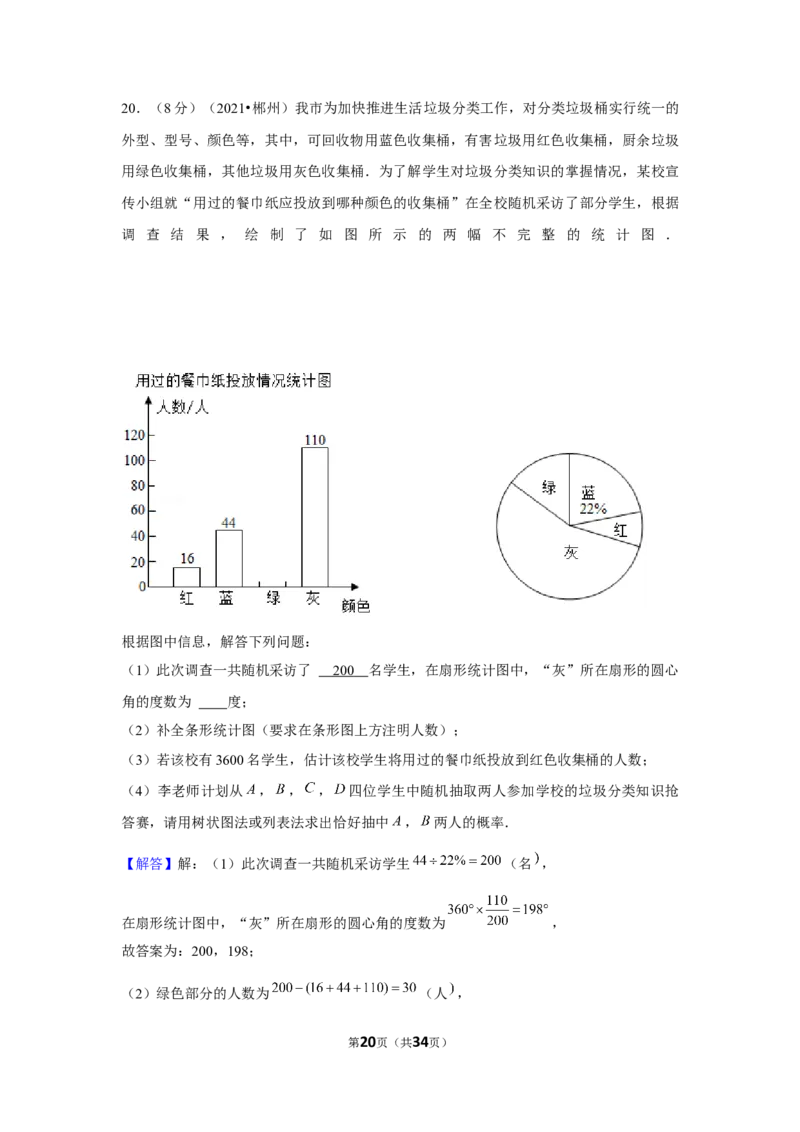
调 查 结 果 , 绘 制 了 如 图 所 示 的 两 幅 不 完 整 的 统 计 图 .
根据图中信息,解答下列问题:
(1)此次调查一共随机采访了 名学生,在扇形统计图中,“灰”所在扇形的圆心角
的度数为 度;
第5页(共34页)(2)补全条形统计图(要求在条形图上方注明人数);
(3)若该校有3600名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;
(4)李老师计划从 , , , 四位学生中随机抽取两人参加学校的垃圾分类知识抢
答赛,请用树状图法或列表法求出恰好抽中 , 两人的概率.
21.(8分)(2021•郴州)如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣
小组为测算电梯 的高度,测得斜坡 米,坡度 ,在 处测得电梯顶端
的仰角 ,求观光电梯 的高度.
(参考数据: , , .结果精确到0.1米)
22.(8分)(2021•郴州)“七 一”建党节前夕,某校决定购买 , 两种奖品,用于
表彰在“童心向党”活动中表现突出的学生.已知 奖品比 奖品每件多25元,预算资金
为1700元,其中800元购买 奖品,其余资金购买 奖品,且购买 奖品的数量是 奖
品的3倍.
(1)求 , 奖品的单价;
(2)购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方
案:不超过预算资金且购买 奖品的资金不少于720元, , 两种奖品共100件,求购
买 , 两种奖品的数量,有哪几种方案?
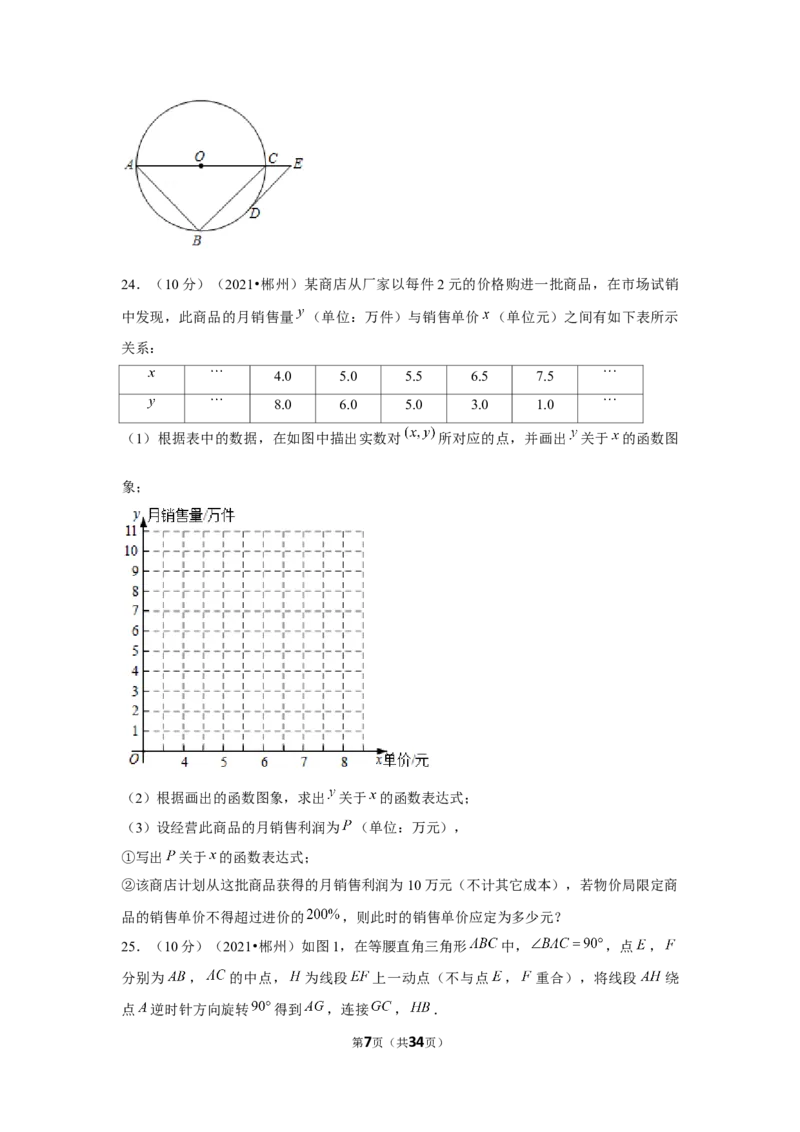
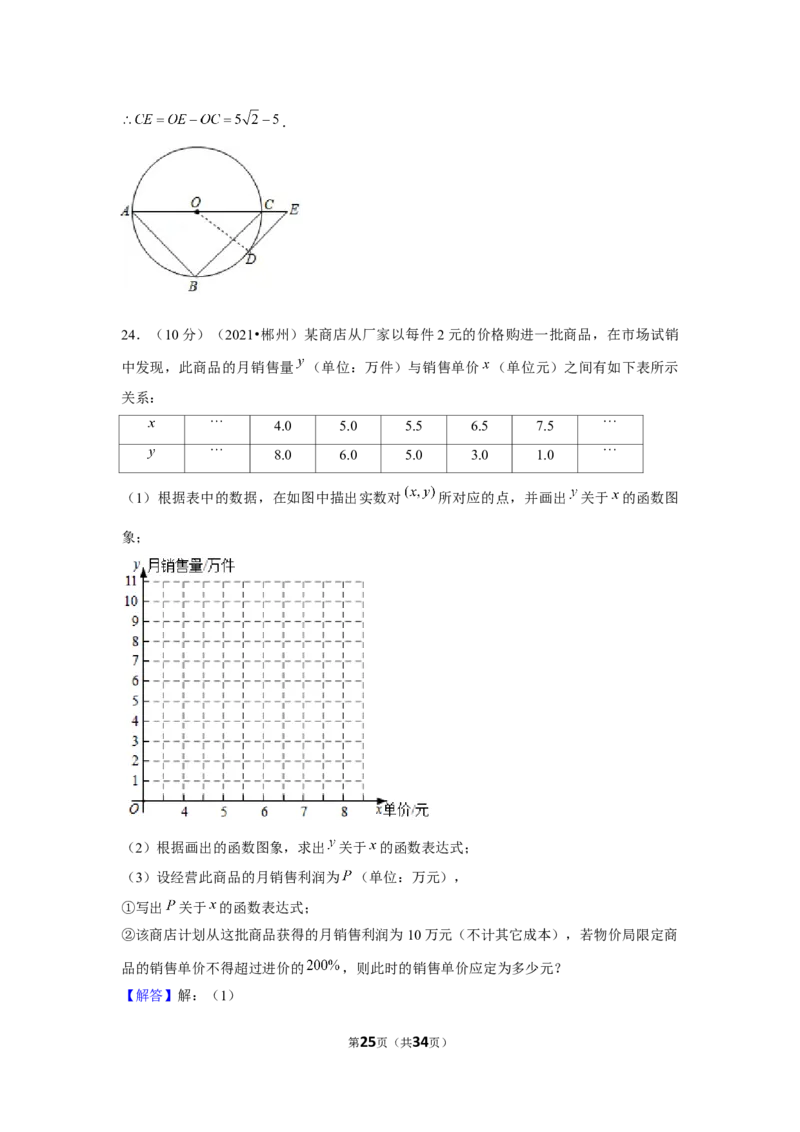
23.(8分)(2021•郴州)如图, 是 的内接三角形, 是 的直径,点
是 的中点, 交 的延长线于点 .
(1)求证:直线 与 相切;
(2)若 的直径是10, ,求 的长.
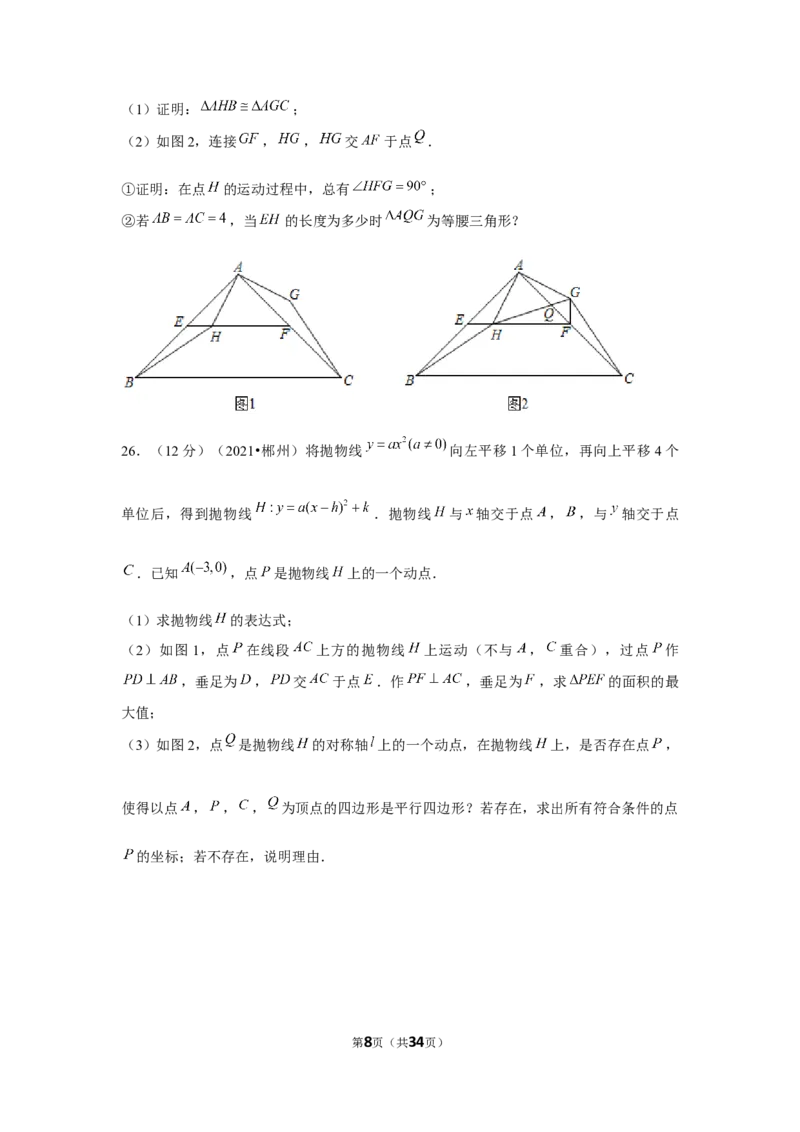
第6页(共34页)24.(10分)(2021•郴州)某商店从厂家以每件2元的价格购进一批商品,在市场试销
中发现,此商品的月销售量 (单位:万件)与销售单价 (单位元)之间有如下表所示
关系:
4.0 5.0 5.5 6.5 7.5
8.0 6.0 5.0 3.0 1.0
(1)根据表中的数据,在如图中描出实数对 所对应的点,并画出 关于 的函数图
象;
(2)根据画出的函数图象,求出 关于 的函数表达式;
(3)设经营此商品的月销售利润为 (单位:万元),
①写出 关于 的函数表达式;
②该商店计划从这批商品获得的月销售利润为10万元(不计其它成本),若物价局限定商
品的销售单价不得超过进价的 ,则此时的销售单价应定为多少元?
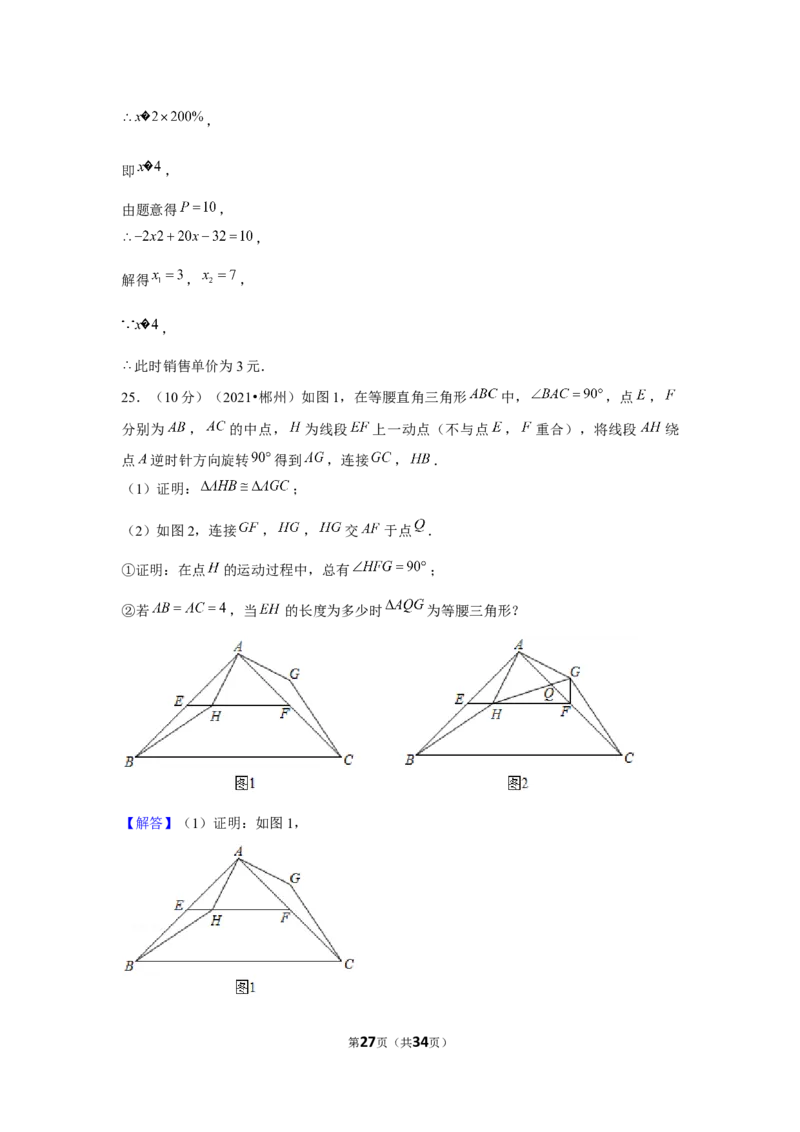
25.(10分)(2021•郴州)如图1,在等腰直角三角形 中, ,点 ,
分别为 , 的中点, 为线段 上一动点(不与点 , 重合),将线段 绕
点 逆时针方向旋转 得到 ,连接 , .
第7页(共34页)(1)证明: ;
(2)如图2,连接 , , 交 于点 .
①证明:在点 的运动过程中,总有 ;
②若 ,当 的长度为多少时 为等腰三角形?
26.(12分)(2021•郴州)将抛物线 向左平移1个单位,再向上平移4个
单位后,得到抛物线 .抛物线 与 轴交于点 , ,与 轴交于点
.已知 ,点 是抛物线 上的一个动点.
(1)求抛物线 的表达式;
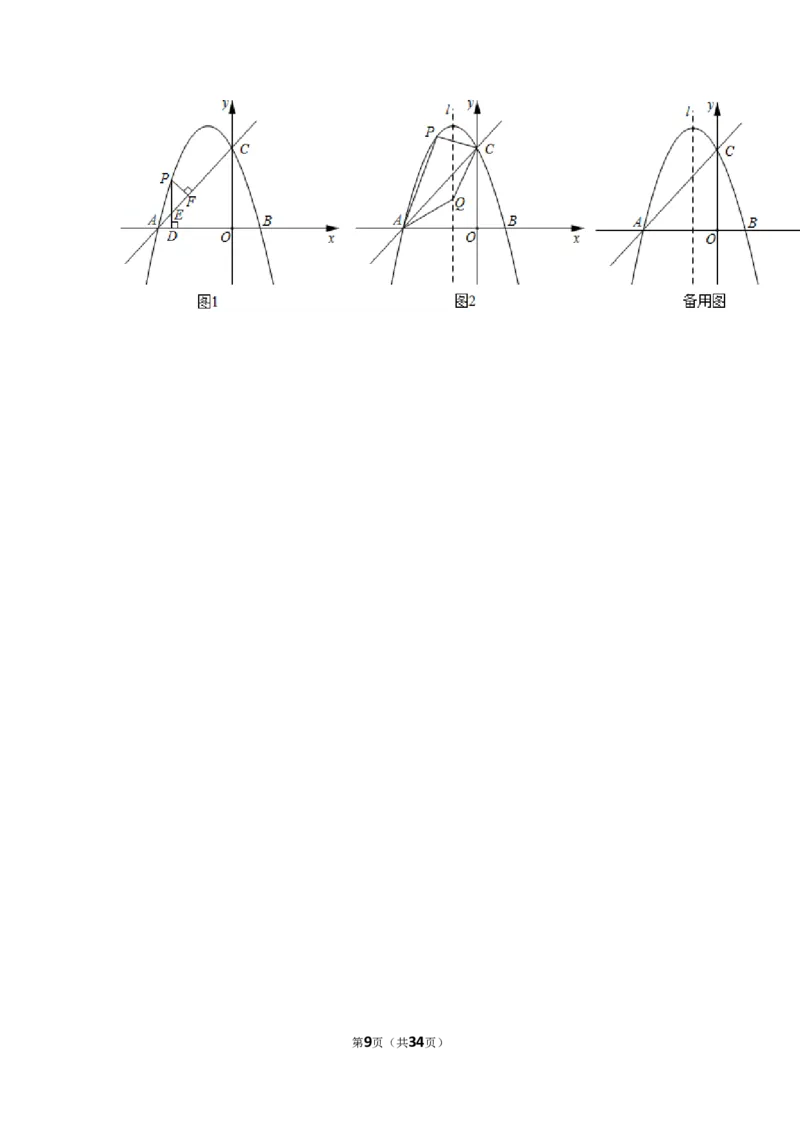
(2)如图1,点 在线段 上方的抛物线 上运动(不与 , 重合),过点 作
,垂足为 , 交 于点 .作 ,垂足为 ,求 的面积的最
大值;
(3)如图2,点 是抛物线 的对称轴 上的一个动点,在抛物线 上,是否存在点 ,
使得以点 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点
的坐标;若不存在,说明理由.
第8页(共34页)第9页(共34页)2021年湖南省郴州市中考数学试卷
参考答案与试题解析
一、选择题(共8小题,每小题3分,共24分)
1.(3分)(2021•郴州)实数 , 在数轴上的位置如图所示,则下列式子正确的是
A. B. C. D.
【解答】解: . , , ,故 项不符合题意;
.由数轴可知 ,故 项符合题意;
. , , ,故 项不符合题意;
. , , , ,故 项不符合题意.
故选: .
2.(3分)(2021•郴州)下列垃圾分类图标分别表示:“可回收垃圾”、“有害垃圾”、
“厨余垃圾”、“其它垃圾”,其中既是轴对称图形,又是中心对称图形的是
A. B.
C. D.
【解答】解: .既不是轴对称图形,也不是中心对称图形.故本选项不合题意;
.既是轴对称图形,又是中心对称图形.故本选项符合题意;
.是轴对称图形,不是中心对称图形.故本选项不合题意;
第10页(共34页).既不是轴对称图形,也不是中心对称图形.故本选项不合题意.
故选: .
3.(3分)(2021•郴州)为响应习近平总书记“坚决打赢关键核心技术攻坚战”的号召,
某科研团队最近攻克了 的光刻机难题,其中 ,则 用科学记数
法表示为
A. B. C. D.
【解答】解: ,
.
故选: .
4.(3分)(2021•郴州)下列运算正确的是
A. B. C. D.
【解答】解: . ,故 选项不符合题意;
. ,故 选项不符合题意;
. ,故 选项符合题意;
. ,故 选项不符合题意;
故选: .
5.(3分)(2021•郴州)下列说法正确的是
A.“明天下雨的概率为 ”,意味着明天有 的时间下雨
B.经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯
C.“某彩票中奖概率是 ”,表示买100张这种彩票一定会有1张中奖
D.小明前几次的数学测试成绩都在90分以上这次数学测试成绩也一定在90分以上
【解答】解: .明天下雨的概率为 ,只是说明明天下雨的可能性大,与时间无关,
故本选项不符合题意;
.经过有信号灯的十字路口时,可能遇到红灯,也可能遇到绿灯,故本选项符合题意;
第11页(共34页).某彩票中奖概率是 ,买100张这种彩票中奖是随机事件,不一定会有1张中奖,故
本选项不符合题意;
.小明前几次的数学测试成绩都在90分以上这次数学测试成绩不一定在90分以上,故
本选项不符合题意.
故选: .
6.(3分)(2021•郴州)已知二元一次方程组 ,则 的值为
A.2 B.6 C. D.
【解答】解: ,
① ②,得 ,
两边都除以3得: ,
故选: .
7.(3分)(2021•郴州)由5个相同的小立方体搭成的物体如图所示,则它的俯视图为
A. B.
C. D.
【解答】解:该组合体的俯视图如下:
第12页(共34页)故选: .
8.(3分)(2021•郴州)如图,在边长为4的菱形 中, ,点 从点 出
发,沿路线 运动.设 点经过的路程为 ,以点 , , 为顶点的三
角形的面积为 ,则下列图象能反映 与 的函数关系的是
A. B.
C. D.
【解答】解:过点 作 于点 ,如图所示:
边长为4的菱形, 中, ,
,
,
第13页(共34页), ,
当点 从点 运动到点 时,过点 作 于点 ,
则 , , ,
,
的面积逐渐增大;
当在线段 上时,
,
的面积保持不变;
当点 在线段 上时,如图,过点 作 交 的延长线于点 ,
则 ,
则 , , ,
,
的面积逐渐减小.
故选: .
二、填空题(共8小题,每小题3分,共24分)
第14页(共34页)9.(3分)(2021•郴州)使 有意义的 的取值范围是 .
【解答】解:使 有意义,则 且 ,
解得: .
故答案为: .
10.(3分)(2021•郴州)在反比例函数 的图象的每一支曲线上,函数值 随自
变量 的增大而增大,则 的取值范围是 .
【解答】解:比例函数 图象上的每一条曲线上, 随 的增大而增大,
,
.
故答案为: .
11.(3分)(2021•郴州)为庆祝中国共产党建党一百周年,某校开展了主题为“我身边
的共产党员”的演讲比赛.比赛从演讲内容、演讲技巧、演讲效果三个方面打分,最终得
分按 的比例计算.若选手甲在演讲内容、演讲技巧、演讲效果三个方面的得分分别
为95分、80分、90分,则选手甲的最终得分为 8 9 分.
【解答】解:选手甲的最终得分为: (分 .
故答案为:89.
12.(3分)(2021•郴州)一个多边形的每一个外角都等于 ,则这个多边形的内角和
为 72 0 度.
【解答】解: 多边形的每一个外角都等于 ,
它的边数为: ,
它的内角和: ,
故答案为:720.
13.(3分)(2021•郴州)关于 的一元二次方程 有两个相等的实数根,则
.
第15页(共34页)【解答】解: 关于 的一元二次方程 有两个相等的实数根,
△ ,
解得: .
故答案为: .
14.(3分)(2021•郴州)如图是一架梯子的示意图,其中 ,且
.为使其更稳固,在 , 间加绑一条安全绳(线段 量得 ,
则 1. 2 .
【解答】解: ,
,
,
,
同理可得: ,
,
,
故答案为:1.2.
15.(3分)(2021•郴州)如图,方老师用一张半径为 的扇形纸板,做了一个圆锥
形帽子(接缝忽略不计).如果圆锥形帽子的半径是 ,那么这张扇形纸板的面积是
第16页(共34页)(结果用含 的式子表示).
【解答】解:这张扇形纸板的面积 .
故答案为 .
16.(3分)(2021•郴州)如图,在 中, , , ,
交 于点 .点 为线段 上的动点,则 的最小值为 .
【解答】解:过点 作 于点 ,过点 作 于点 ,
,
,
第17页(共34页), ,
,
由勾股定理得 ,
,
,
,
即点 、 、 三点共线时, 最小,
的最小值为 的长,
,
,
.
的最小值为 .
故答案为: .
三、解答题(17~19题每题6分,20~23题每题8分,24~25题每题10分,26题12分,
共82分)
17.(6分)(2021•郴州)计算: .
【解答】解:原式
.
18.(6分)(2021•郴州)先化简,再求值: ,其中 .
第18页(共34页)【解答】解:
,
当 时,原式 .
19.(6分)(2021•郴州)如图,四边形 中, ,将对角线 向两端分别
延长至点 , ,使 .连接 , ,若 .证明:四边形 是平
行四边形.
【解答】证明:在 和 中,
,
,
,
,
,
四边形 是平行四边形.
第19页(共34页)20.(8分)(2021•郴州)我市为加快推进生活垃圾分类工作,对分类垃圾桶实行统一的
外型、型号、颜色等,其中,可回收物用蓝色收集桶,有害垃圾用红色收集桶,厨余垃圾
用绿色收集桶,其他垃圾用灰色收集桶.为了解学生对垃圾分类知识的掌握情况,某校宣
传小组就“用过的餐巾纸应投放到哪种颜色的收集桶”在全校随机采访了部分学生,根据
调 查 结 果 , 绘 制 了 如 图 所 示 的 两 幅 不 完 整 的 统 计 图 .
根据图中信息,解答下列问题:
(1)此次调查一共随机采访了 20 0 名学生,在扇形统计图中,“灰”所在扇形的圆心
角的度数为 度;
(2)补全条形统计图(要求在条形图上方注明人数);
(3)若该校有3600名学生,估计该校学生将用过的餐巾纸投放到红色收集桶的人数;
(4)李老师计划从 , , , 四位学生中随机抽取两人参加学校的垃圾分类知识抢
答赛,请用树状图法或列表法求出恰好抽中 , 两人的概率.
【解答】解:(1)此次调查一共随机采访学生 (名 ,
在扇形统计图中,“灰”所在扇形的圆心角的度数为 ,
故答案为:200,198;
(2)绿色部分的人数为 (人 ,
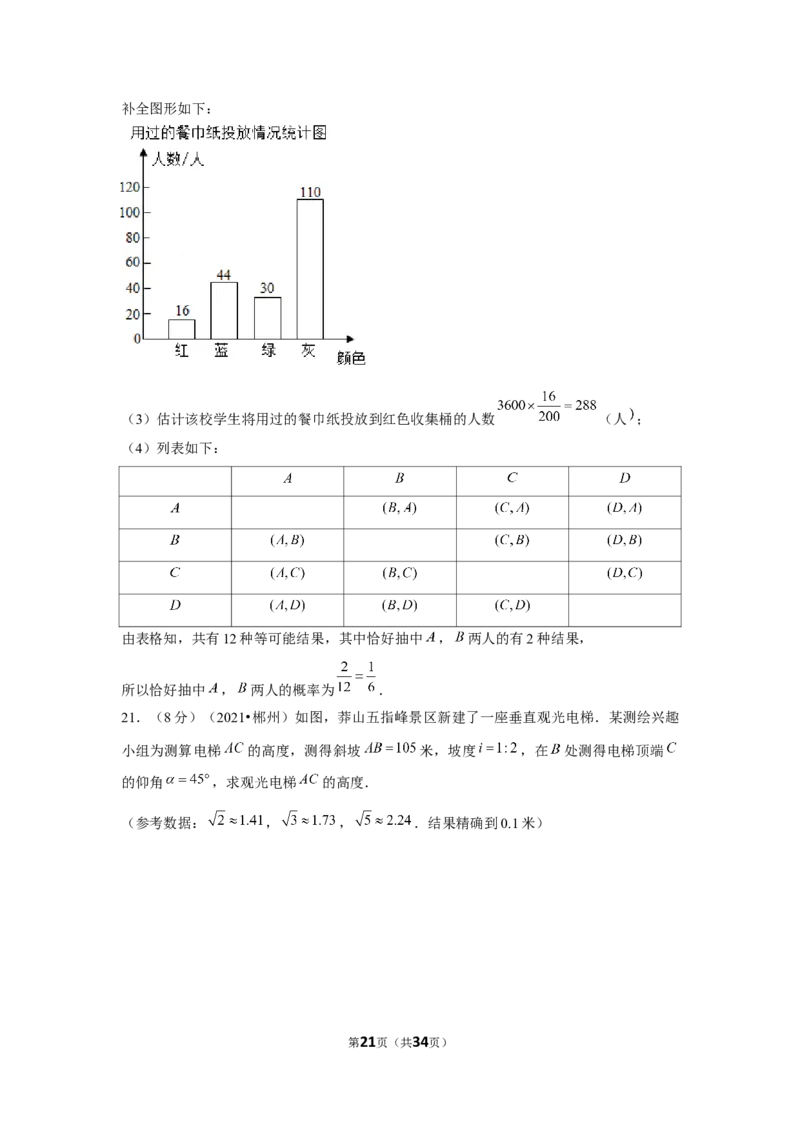
第20页(共34页)补全图形如下:
(3)估计该校学生将用过的餐巾纸投放到红色收集桶的人数 (人 ;
(4)列表如下:
由表格知,共有12种等可能结果,其中恰好抽中 , 两人的有2种结果,
所以恰好抽中 , 两人的概率为 .
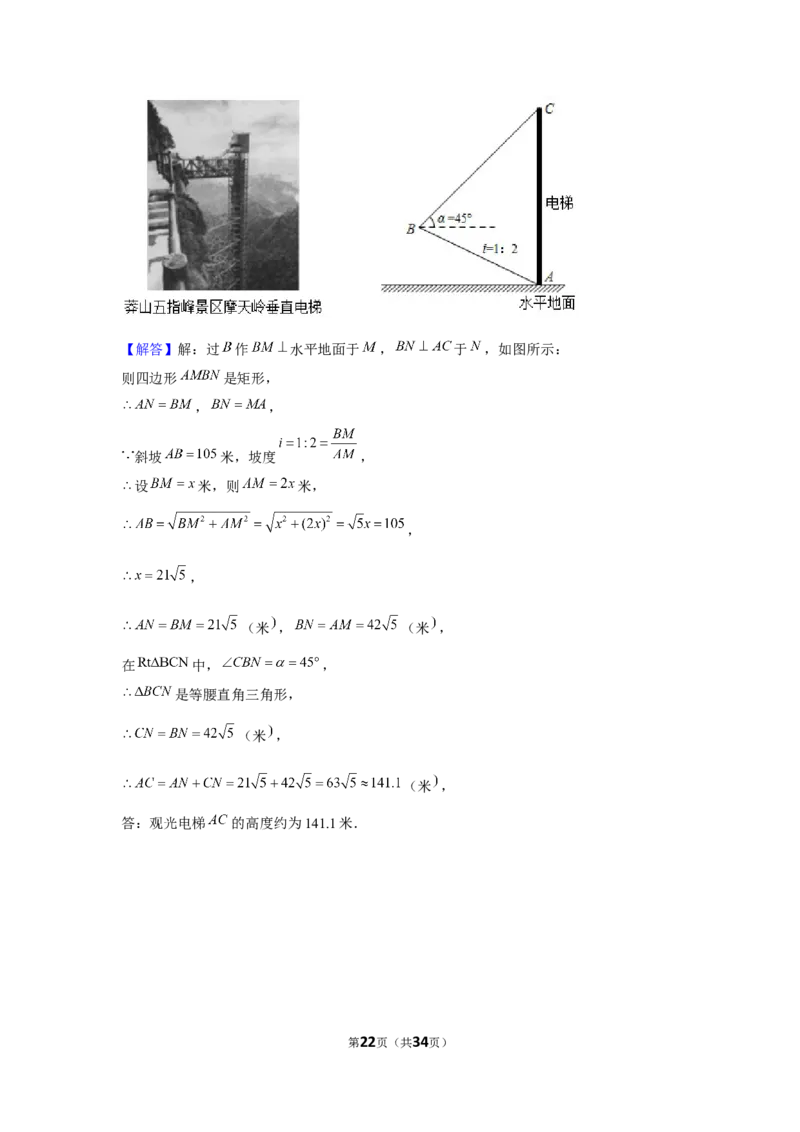
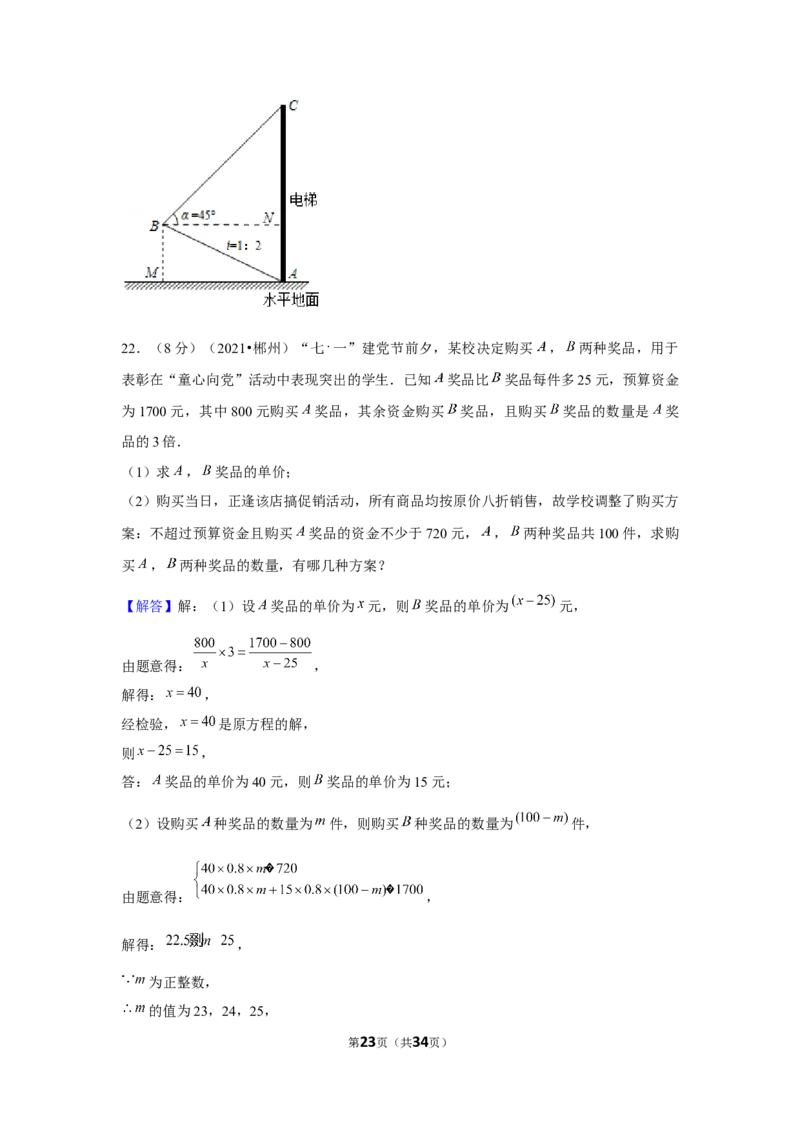
21.(8分)(2021•郴州)如图,莽山五指峰景区新建了一座垂直观光电梯.某测绘兴趣
小组为测算电梯 的高度,测得斜坡 米,坡度 ,在 处测得电梯顶端
的仰角 ,求观光电梯 的高度.
(参考数据: , , .结果精确到0.1米)
第21页(共34页)【解答】解:过 作 水平地面于 , 于 ,如图所示:
则四边形 是矩形,
, ,
斜坡 米,坡度 ,
设 米,则 米,
,
,
(米 , (米 ,
在 中, ,
是等腰直角三角形,
(米 ,
(米 ,
答:观光电梯 的高度约为141.1米.
第22页(共34页)22.(8分)(2021•郴州)“七 一”建党节前夕,某校决定购买 , 两种奖品,用于
表彰在“童心向党”活动中表现突出的学生.已知 奖品比 奖品每件多25元,预算资金
为1700元,其中800元购买 奖品,其余资金购买 奖品,且购买 奖品的数量是 奖
品的3倍.
(1)求 , 奖品的单价;
(2)购买当日,正逢该店搞促销活动,所有商品均按原价八折销售,故学校调整了购买方
案:不超过预算资金且购买 奖品的资金不少于720元, , 两种奖品共100件,求购
买 , 两种奖品的数量,有哪几种方案?
【解答】解:(1)设 奖品的单价为 元,则 奖品的单价为 元,
由题意得: ,
解得: ,
经检验, 是原方程的解,
则 ,
答: 奖品的单价为40元,则 奖品的单价为15元;
(2)设购买 种奖品的数量为 件,则购买 种奖品的数量为 件,
由题意得: ,
解得: ,
为正整数,
的值为23,24,25,
第23页(共34页)有三种方案:
①购买 种奖品23件, 种奖品77件;
②购买 种奖品24件, 种奖品76件;
③购买 种奖品25件, 种奖品75件.
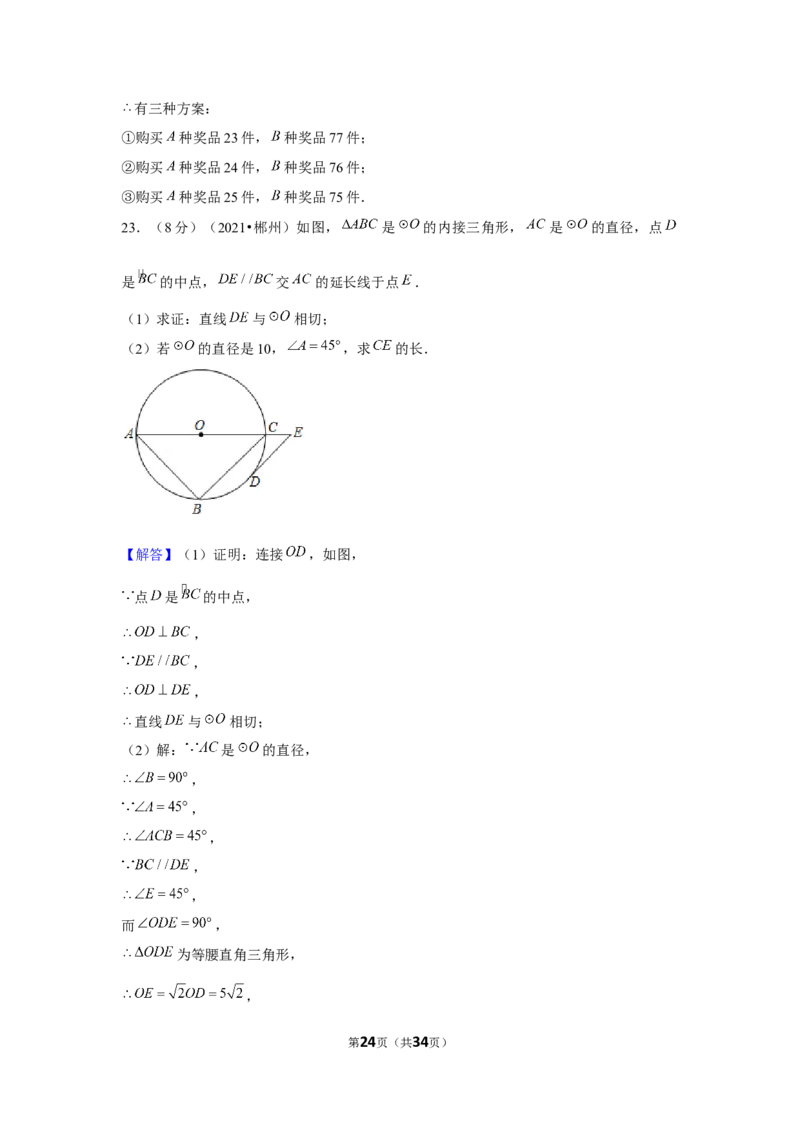
23.(8分)(2021•郴州)如图, 是 的内接三角形, 是 的直径,点
是 的中点, 交 的延长线于点 .
(1)求证:直线 与 相切;
(2)若 的直径是10, ,求 的长.
【解答】(1)证明:连接 ,如图,
点 是 的中点,
,
,
,
直线 与 相切;
(2)解: 是 的直径,
,
,
,
,
,
而 ,
为等腰直角三角形,
,
第24页(共34页).
24.(10分)(2021•郴州)某商店从厂家以每件2元的价格购进一批商品,在市场试销
中发现,此商品的月销售量 (单位:万件)与销售单价 (单位元)之间有如下表所示
关系:
4.0 5.0 5.5 6.5 7.5
8.0 6.0 5.0 3.0 1.0
(1)根据表中的数据,在如图中描出实数对 所对应的点,并画出 关于 的函数图
象;
(2)根据画出的函数图象,求出 关于 的函数表达式;
(3)设经营此商品的月销售利润为 (单位:万元),
①写出 关于 的函数表达式;
②该商店计划从这批商品获得的月销售利润为10万元(不计其它成本),若物价局限定商
品的销售单价不得超过进价的 ,则此时的销售单价应定为多少元?
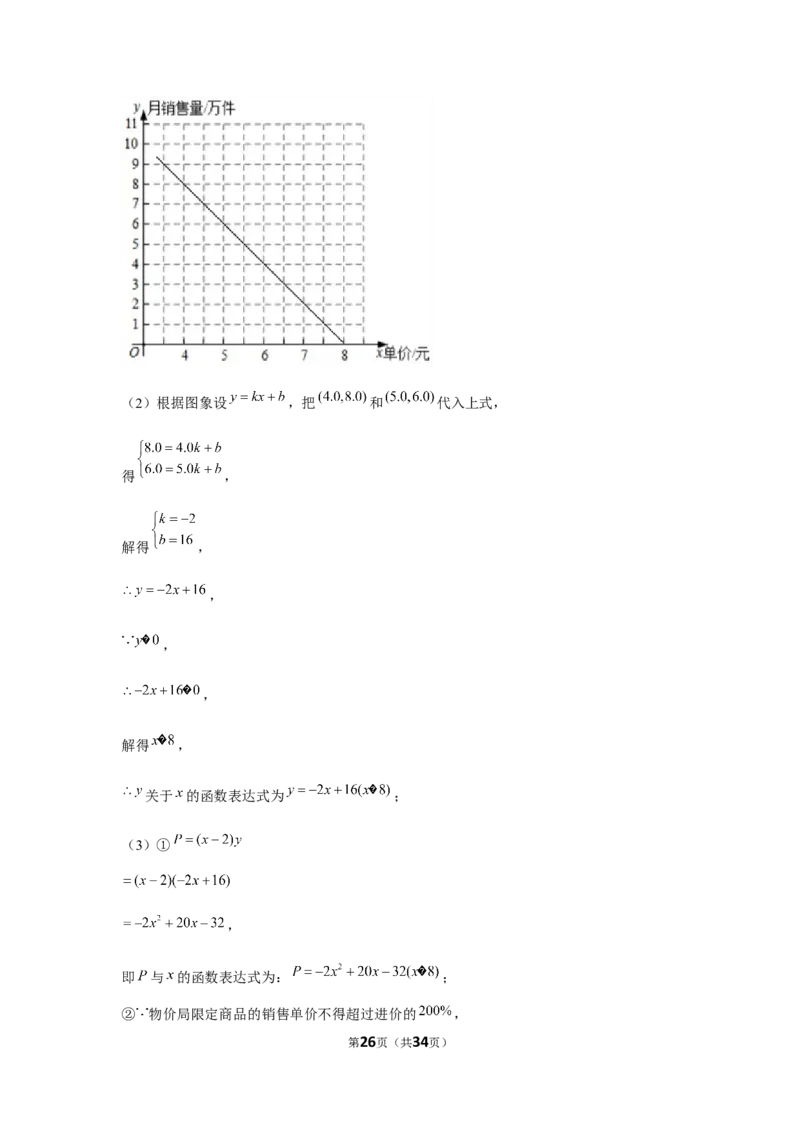
【解答】解:(1)
第25页(共34页)(2)根据图象设 ,把 和 代入上式,
得 ,
解得 ,
,
,
,
解得 ,
关于 的函数表达式为 ;
(3)①
,
即 与 的函数表达式为: ;
② 物价局限定商品的销售单价不得超过进价的 ,
第26页(共34页),
即 ,
由题意得 ,
,
解得 , ,
,
此时销售单价为3元.
25.(10分)(2021•郴州)如图1,在等腰直角三角形 中, ,点 ,
分别为 , 的中点, 为线段 上一动点(不与点 , 重合),将线段 绕
点 逆时针方向旋转 得到 ,连接 , .
(1)证明: ;
(2)如图2,连接 , , 交 于点 .
①证明:在点 的运动过程中,总有 ;
②若 ,当 的长度为多少时 为等腰三角形?
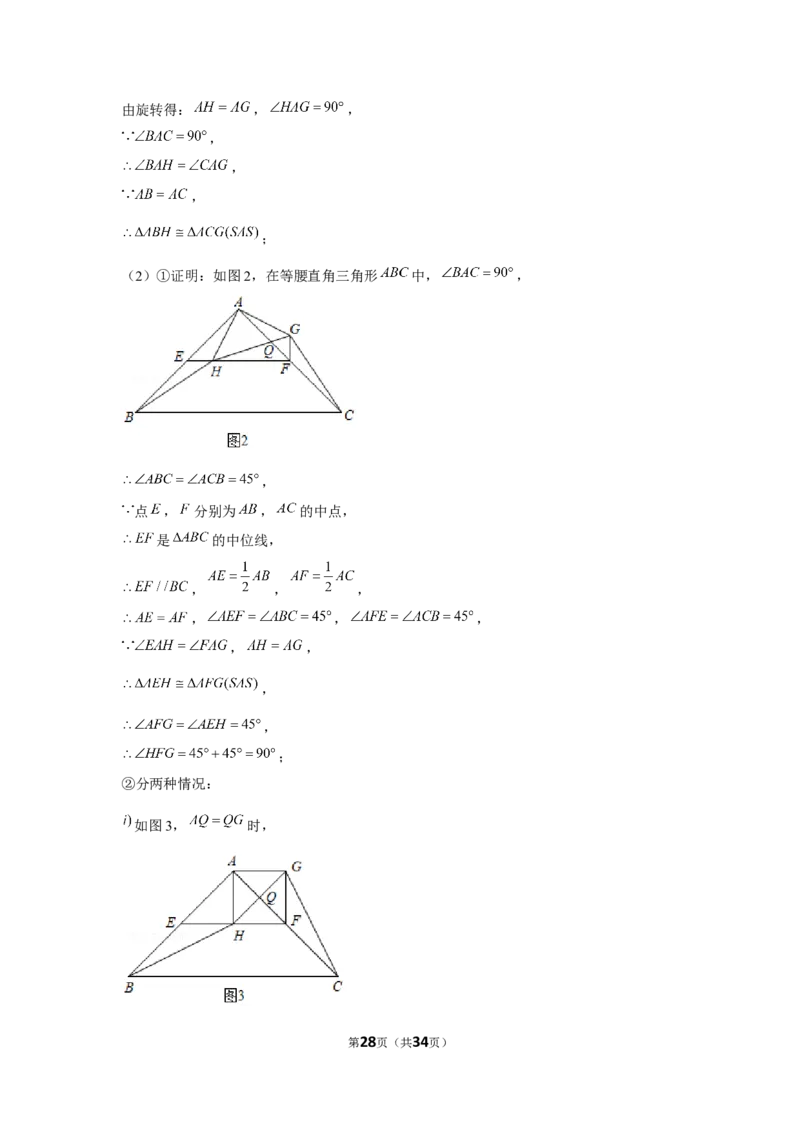
【解答】(1)证明:如图1,
第27页(共34页)由旋转得: , ,
,
,
,
;
(2)①证明:如图2,在等腰直角三角形 中, ,
,
点 , 分别为 , 的中点,
是 的中位线,
, , ,
, , ,
, ,
,
,
;
②分两种情况:
如图3, 时,
第28页(共34页),
,
,
,
,
,
,
,
,
,
四边形 是正方形,
,
,
,
当 的长度为 时, 为等腰三角形;
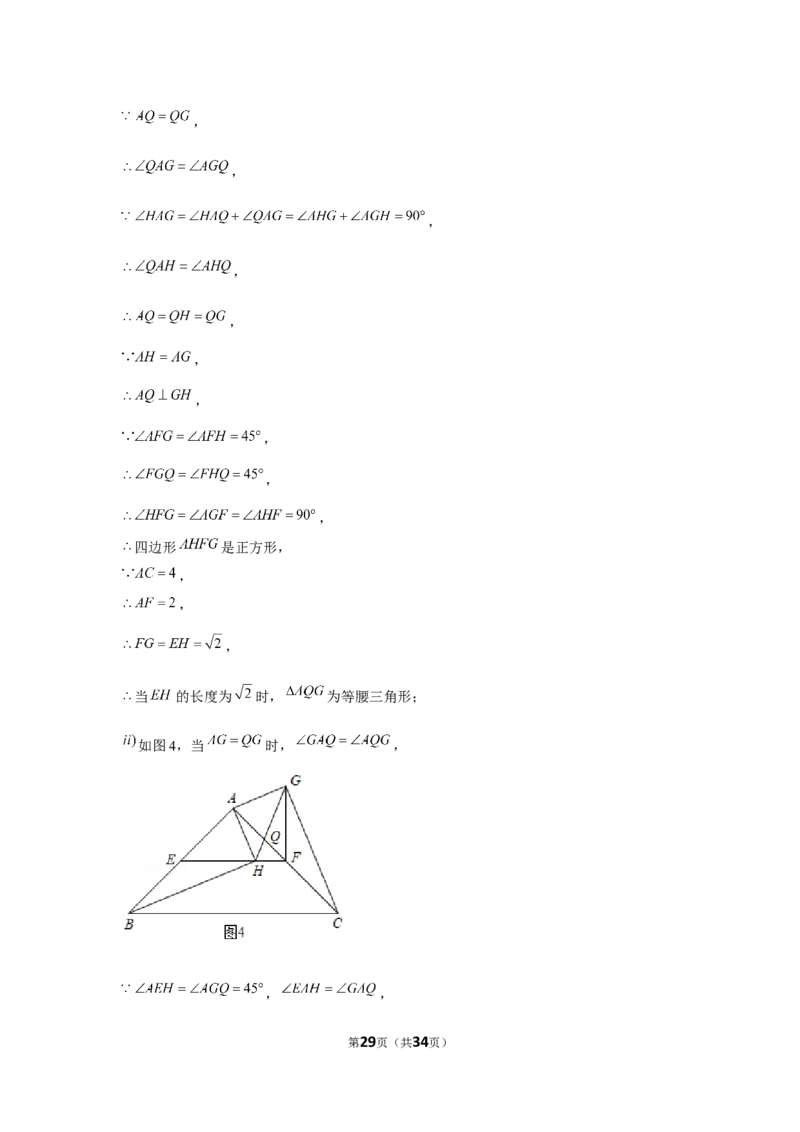
如图4,当 时, ,
, ,
第29页(共34页),
,
当 的长度为2时, 为等腰三角形;
综上,当 的长度为 或2时, 为等腰三角形.
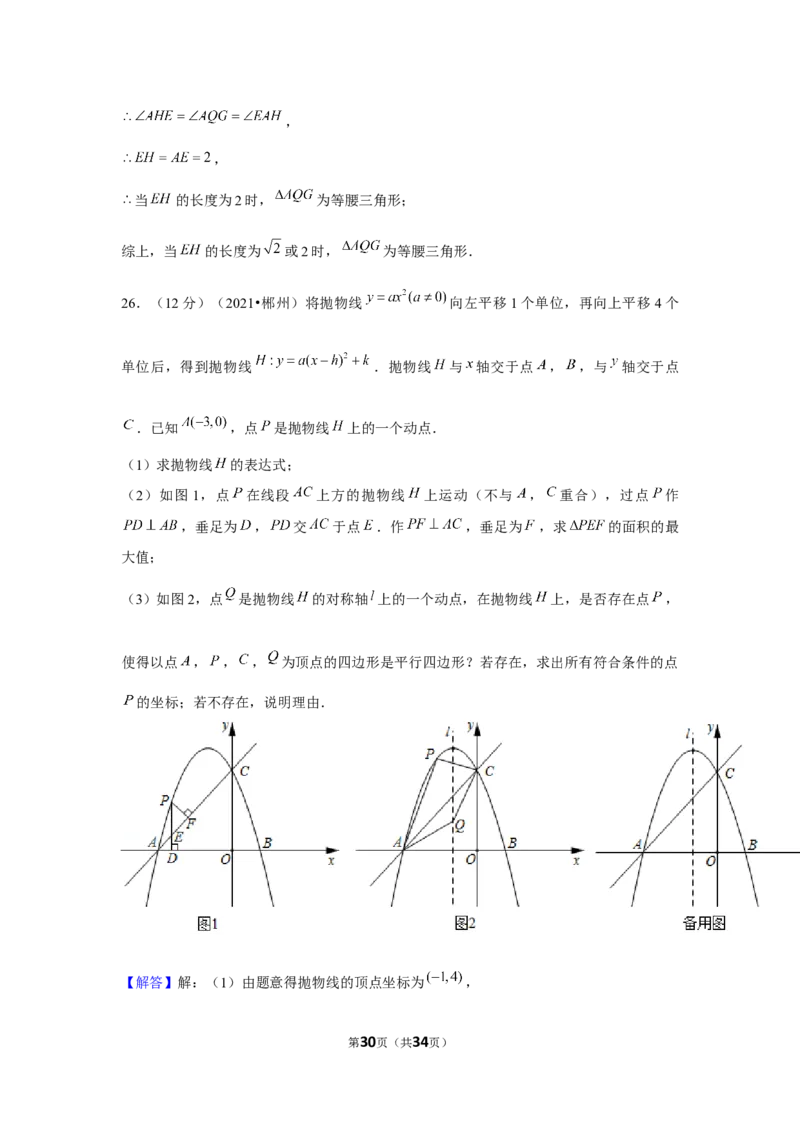
26.(12分)(2021•郴州)将抛物线 向左平移1个单位,再向上平移4个
单位后,得到抛物线 .抛物线 与 轴交于点 , ,与 轴交于点
.已知 ,点 是抛物线 上的一个动点.
(1)求抛物线 的表达式;
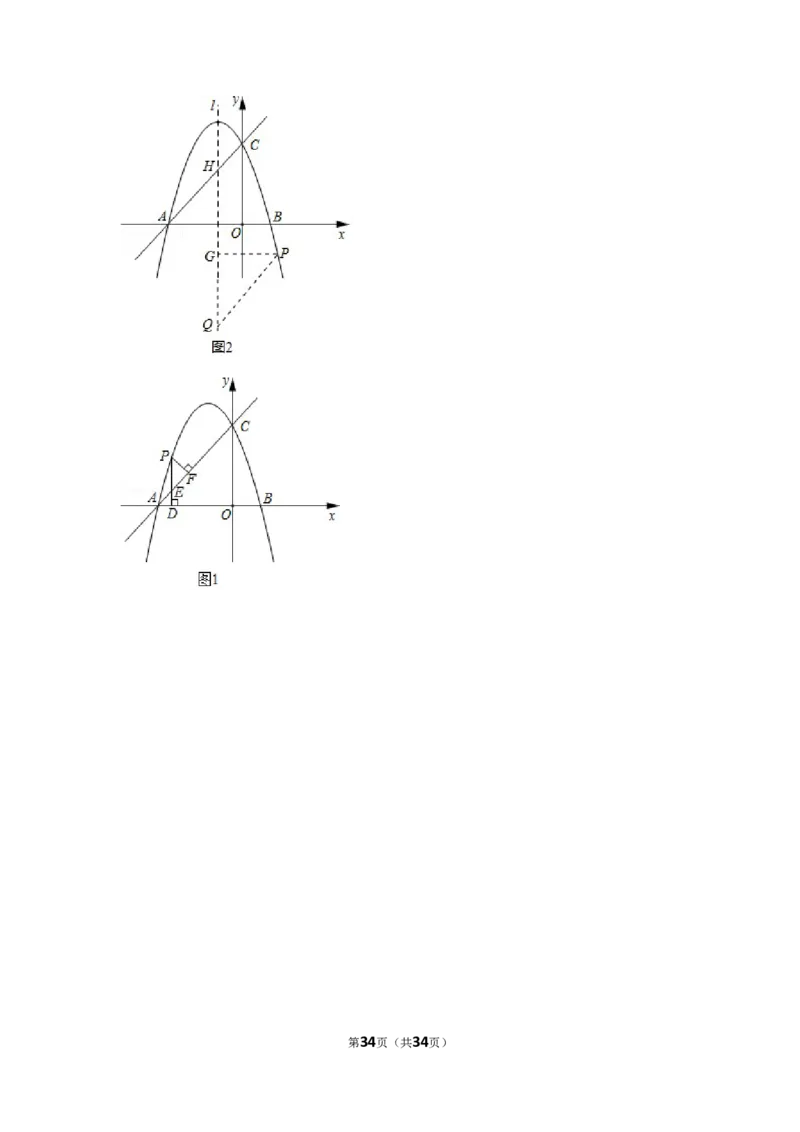
(2)如图1,点 在线段 上方的抛物线 上运动(不与 , 重合),过点 作
,垂足为 , 交 于点 .作 ,垂足为 ,求 的面积的最
大值;
(3)如图2,点 是抛物线 的对称轴 上的一个动点,在抛物线 上,是否存在点 ,
使得以点 , , , 为顶点的四边形是平行四边形?若存在,求出所有符合条件的点
的坐标;若不存在,说明理由.
【解答】解:(1)由题意得抛物线的顶点坐标为 ,
第30页(共34页)抛物线 ,
将 代入,得: ,
解得: ,
抛物线 的表达式为 ;
(2)如图1,由(1)知: ,
令 ,得 ,
,
设直线 的解析式为 ,
, ,
,
解得: ,
直线 的解析式为 ,
设 ,则 ,
,
,
当 时, 有最大值 ,
, ,
是等腰直角三角形,
,
,
,
第31页(共34页),
,
,
,
是等腰直角三角形,
,
,
当 时, ;
(3)①当 为平行四边形的边时,则有 ,且 ,
如图2,过点 作对称轴的垂线,垂足为 ,设 交对称轴于点 ,
则 ,
在 和 中,
,
,
,
点 到对称轴的距离为3,
又 ,
抛物线对称轴为直线 ,
设点 ,则 ,
解得: 或 ,
当 时, ,
第32页(共34页)当 时, ,
点 坐标为 或 ;
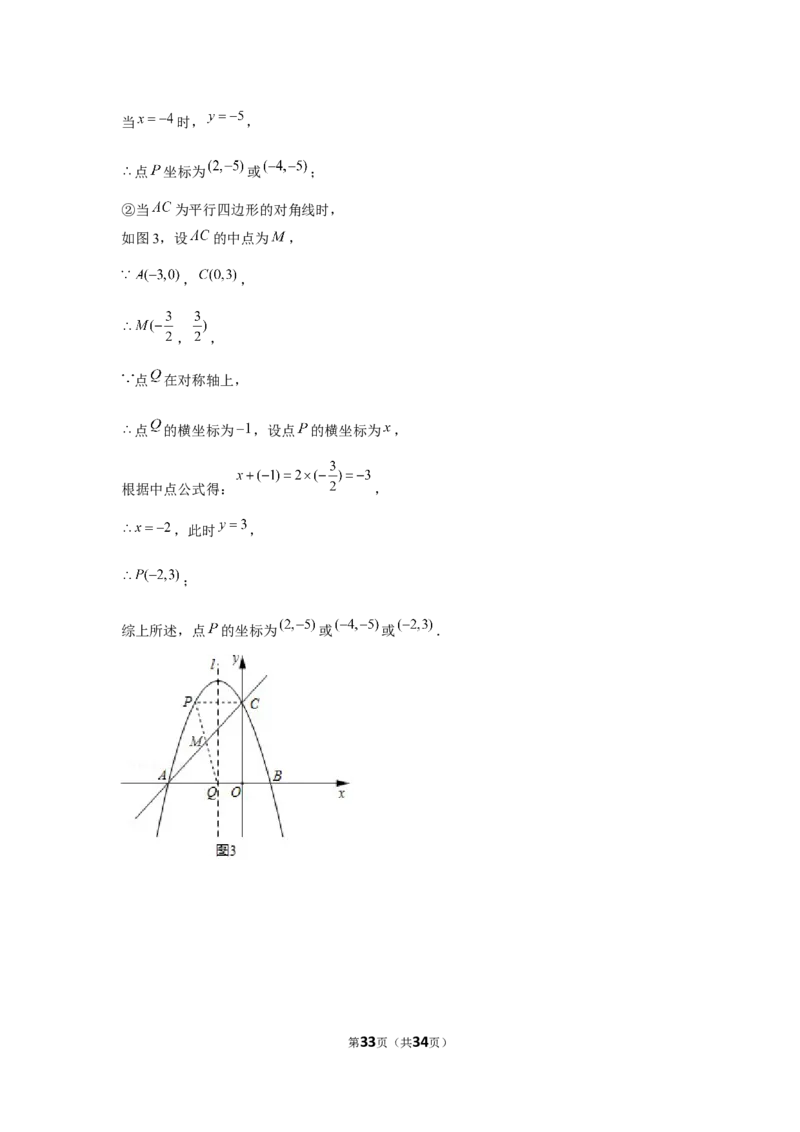
②当 为平行四边形的对角线时,
如图3,设 的中点为 ,
, ,
, ,
点 在对称轴上,
点 的横坐标为 ,设点 的横坐标为 ,
根据中点公式得: ,
,此时 ,
;
综上所述,点 的坐标为 或 或 .
第33页(共34页)声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/9/13 17:16:08;用户:初中数学61;邮箱:ydyd61@xyh.com;学号:36810736
第34页(共34页)