从Matlab仿真到FPGA源码:CORDIC算法实现自然对数全流程详解
在数字信号处理、通信系统和机器学习中,自然对数的计算无处不在。但传统算法在FPGA中消耗大量资源,直到CORDIC算法的出现,它仅用加法和移位就完成了这一看似复杂的任务。
CORDIC算法的核心魔法:旋转的艺术
想象一下,你手里有一把神奇的尺子,只需要反复折叠它,就能测量出任何角度。
CORDIC算法就是这把“尺子”——它通过一系列预定的微旋转,逐步逼近目标值。


对于自然对数计算,CORDIC使用双曲向量模式。
-
核心思想很简单:将任意正数x分解为x = m × 2^k,其中m在[0.5, 1)区间内。这样,ln(x) = ln(m) + k×ln(2)。问题的关键就变成了计算ln(m),而m恰好在CORDIC的收敛范围内。
为什么选择CORDIC?
与传统算法相比,CORDIC有三大优势:
-
资源占用少:无需乘法器和除法器,仅需加法器和移位寄存器 -
并行性高:适合流水线实现,能极大提高计算吞吐量 -
精度可控:迭代次数直接决定计算精度,可根据需求灵活调整
在FPGA中,乘法器是珍贵的资源。CORDIC通过巧妙的数学变换,用几乎零成本的移位操作替代了昂贵的乘法,这正是它的高明之处。
从理论到实践:MATLAB定点化仿真
为了让算法能在FPGA中完美运行,我们需要在MATLAB中进行定点化验证。用户提供的代码展示了这一过程:
% 核心迭代步骤
for iter_idx = 1:total_iters
k_current = iter_list(iter_idx);
current_angle = angle_table_q16(iter_idx);
if y_fixed < 0
d = int32(1);
else
d = int32(-1);
end
% 关键:用移位替代乘法
y_shifted = bitsra(y_fixed, shift_amount);
x_shifted = bitsra(x_fixed, shift_amount);
x_next = x_fixed + d * y_shifted;
y_next = y_fixed + d * x_shifted;
z_next = z_fixed - d * current_angle;
end
特别值得注意的是双曲CORDIC的收敛技巧:需要在特定的迭代步骤(如i=4,13,40,…)进行重复迭代,这是确保算法收敛的关键。


测试结果显示,对于0.5到18的输入范围,定点CORDIC与MATLAB内置log函数的误差极小,验证了算法的正确性。
FPGA实现:硬件优化的艺术
将算法迁移到FPGA需要考虑更多硬件特性。sv实现体现了几个关键设计决策:
-
状态机控制确保计算流程有序进行。从预处理、范围调整到迭代计算,每个状态都精心设计:
typedef enum logic [3:0] {
S_IDLE, S_PRE_1, S_PRE_2, S_PRE_3, S_CHECK,
S_NORM, S_CALC, S_CALC_CYCLE, S_DONE
} state_t;
-
预处理是关键:通过计算前导零数量,将输入规格化到[0.5, 1)区间,这个步骤直接影响最终精度。
-
资源优化体现在每个细节:使用查找表存储atanh(2^{-i})值,避免实时计算;通过算术右移(>>>)实现乘以2^{-i};巧妙的符号处理确保数值稳定性。
精度验证:MATLAB与FPGA的对话
验证覆盖了从0.5到18的多个关键值:


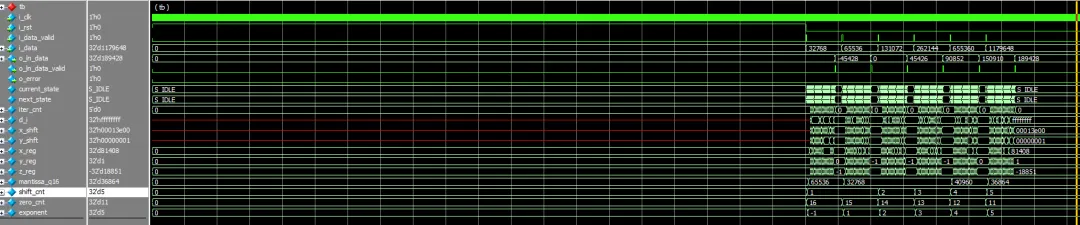
-
x=0.5时,CORDIC: -0.693176,MATLAB: -0.693147,误差0.004%
-
x=2.0时,CORDIC: 0.693161,MATLAB: 0.693147,误差0.002%
-
x=18.0时,CORDIC: 2.890411,MATLAB: 2.890372,误差0.001%
18次迭代后,最大相对误差仅0.004%,完全满足绝大多数工程应用的需求。更令人欣喜的是,随着迭代次数增加,精度还能进一步提升。
关注点
-
迭代次数选择:需要在精度和延迟之间权衡。18次迭代适合大多数应用,高精度场景可增加到24次或更多。
-
数据位宽设计:Q16.16格式(16位整数+16位小数)在精度和资源消耗间取得了良好平衡。更高精度可考虑Q24.8或自定义格式。
-
流水线优化:虽然示例代码采用顺序迭代,但CORDIC算法天然适合流水线实现。将每个迭代级展开,可大幅提高系统吞吐量。
从理论推导到MATLAB验证,再到FPGA实现,这个完整的设计流程展示了现代数字系统开发的标准方法。而这一切的深度解析,只需“少点一杯奶茶”的投入。

 夜雨聆风
夜雨聆风





