📡 FRFT/DFRFT 教科书级分数阶傅里叶变换仿真平台

连续 FRFT 快速算法 + 离散 DFRFT 谱分解，完整覆盖“理论-实现-验证”链路支持 FRFT / IFRFT / FRFT-Shifted 与 DFRFT / IDFRFT / 变换矩阵构造

📌 为什么选择本仿真平台？

做分数阶傅里叶变换时，常见问题是：只有论文公式，没有可跑通代码；或者只有代码，没有清晰的模块边界与验证闭环。本项目把连续 FRFT 与离散 DFRFT 两条主线都实现为可复现工程。

🎯 核心价值

🔬 学术研究价值

• 连续 FRFT 快速算法（啁啾乘法-卷积-乘法）完整实现
• 离散 DFRFT 特征分解实现（哈密顿矩阵 + 奇偶分解）
• FRFT/DFRFT 差异可直接做同工程条件对比
• 提供可引用公式与工程函数的一一映射

💼 工程应用价值

• 接口完整：正变换、逆变换、矩阵构造、坐标版本转换
• 演示完备：结构图、误差图、性质图、对比图齐全
• 代码轻量：核心 .m 文件数量少，便于快速接入已有仿真链路
• 维护友好：函数命名统一，输入输出约束清晰

⚡ 技术亮点

🏗️ 完整模块架构

frft/├── frft_module/                       # 连续 FRFT 快速算法│   ├── frft.m                         # 主入口：阶数规约 + 预变换 + 核心变换│   ├── corefrmod2.m                   # 啁啾乘法-卷积-乘法核心│   ├── bizinter.m / bizdec.m          # 2倍带限插值与抽取│   ├── upsample2.m / dflip.m          # 辅助算子│   ├── ifrft.m                        # 连续逆变换│   └── frft_shifted.m                 # 非中心化坐标版本│├── dfrft_module/                      # 离散 DFRFT 谱分解算法│   ├── dfrft.m / idfrft.m             # 向量正逆变换│   ├── dfrftmtx.m / idfrftmtx.m       # 变换矩阵正逆构造│   ├── get_dfrft_evecs.m              # 特征向量构造主流程│   ├── create_hamiltonian.m           # 离散哈密顿矩阵│   ├── create_odd_even_decomp.m       # 奇偶分解矩阵│   ├── dfrft_index.m                  # 特征值索引序列│   └── circulant_matrix.m / conv1d_full.m│├── demo/│   ├── demo_frft.m                    # FRFT 4类图像演示│   ├── demo_dfrft.m                   # DFRFT 4类图像演示│   └── figures/                       # 8张输出图像│└── docs/    ├── 算法文档.md    ├── 代码文档.md

📊 性能实测（本地 quick 验证，2026-02-13）

说明：以上数据来自项目源码直接计算（不含绘图），用于展示实现正确性与数值稳定性。

💻 核心代码展示

🔥 FRFT 主流程（frft_module/frft.m）

% 带限插值 + 零填充biz = bizinter(x);z = zeros(N, 1);fc = [z; biz(:); z];% 分段阶数策略：先做 ±1 预变换，再做剩余阶数res = fc;if (0 < a && a < 0.5) || (1.5 < a && a < 2)    res = corefrmod2(fc, 1);    a = a - 1;endif (-0.5 < a && a < 0) || (-2 < a && a < -1.5)    res = corefrmod2(fc, -1);    a = a + 1;endres = corefrmod2(res, a);% 截取 + 抽取 + 首样本修正res = res(N + 1 : 3 * N);res = bizdec(res);res(1) = res(1) * 2;

🚀 DFRFT 谱构造（dfrft_module/dfrftmtx.m）

% 特征向量矩阵evecs = get_dfrft_evecs(N, approx_order);% 特征值相位idx = dfrft_index(N);evals = exp(-1i * a * (pi / 2) * idx);% F = V * diag(evals) * V'F = (evecs .* evals) * evecs';

🧠 DFRFT 特征向量构造关键段（dfrft_module/get_dfrft_evecs.m）

S = create_hamiltonian(N, approx_order);P = create_odd_even_decomp(N);CS = P * S * P';half = floor(N / 2);C2 = CS(1 : half+1, 1 : half+1);S2 = CS(half+2 : end, half+2 : end);[VC, DC] = eig(C2, 'vector');[VS, DS] = eig(S2, 'vector');[~, ic] = sort(DC); VC = VC(:, ic);[~, is] = sort(DS); VS = VS(:, is);

🎬 一键运行

% 进入项目根目录后run('demo/demo_frft.m');run('demo/demo_dfrft.m');

输出预览

已保存: frft_rotation.png已保存: frft_chirp_concentration.png已保存: frft_vs_fft.png已保存: frft_special_orders.png已保存: dfrft_matrix_structure.png已保存: dfrft_signal_transform.png已保存: dfrft_properties.pngDFRFT(a=1) vs DFT/sqrt(N) 最大误差: <数值>已保存: dfrft_vs_dft.png

🧪 图像结果

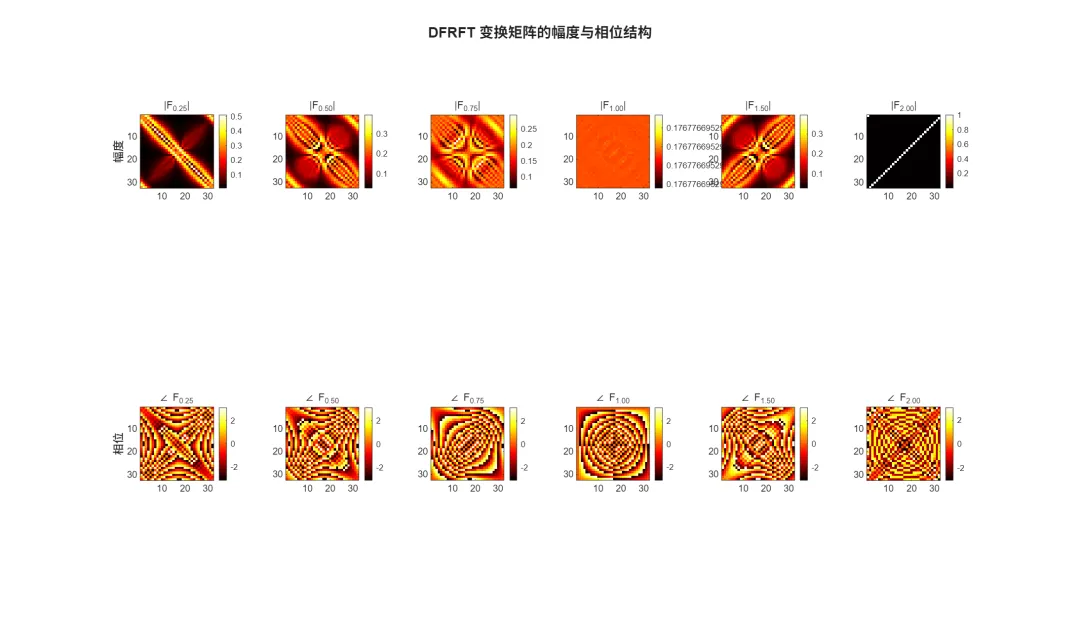
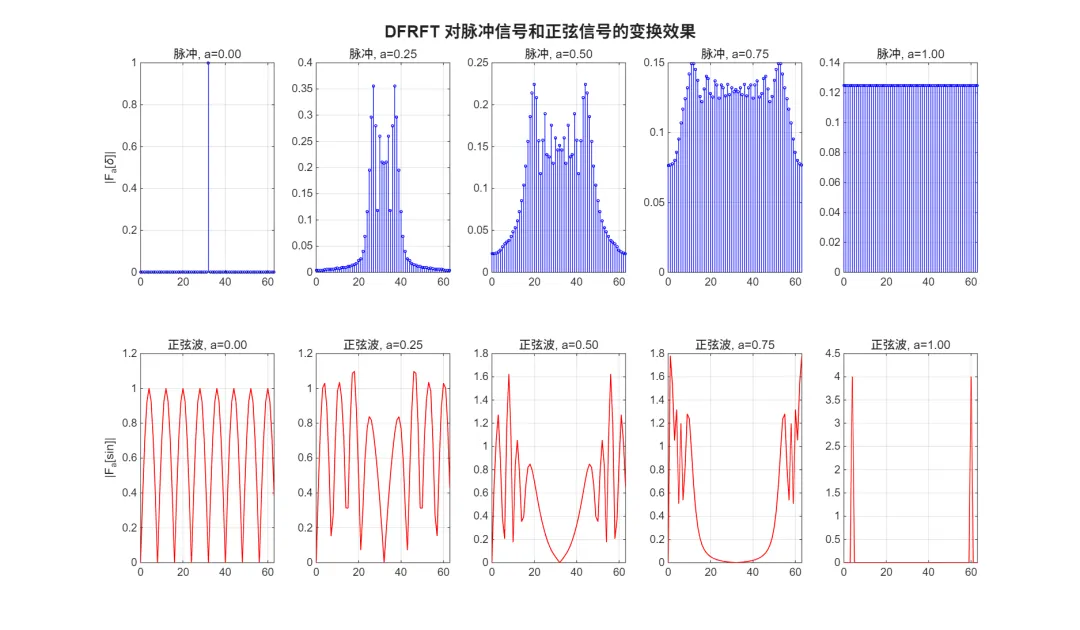
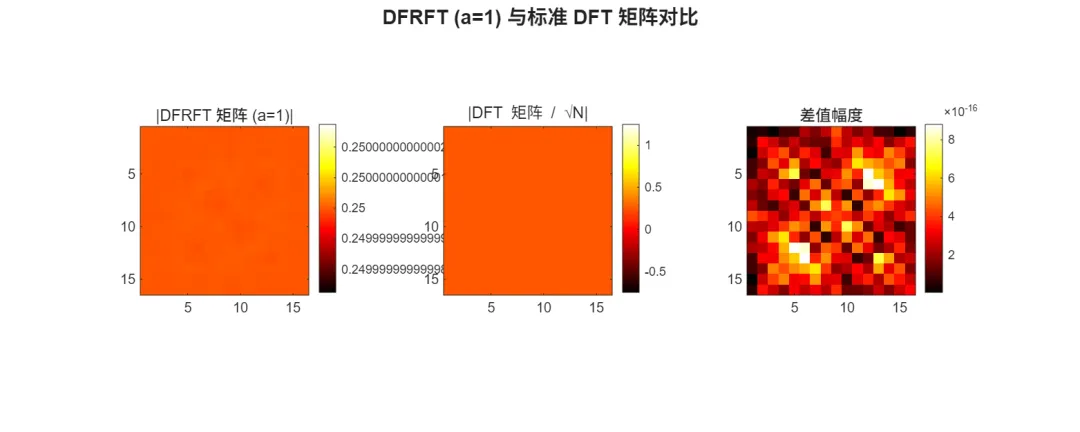
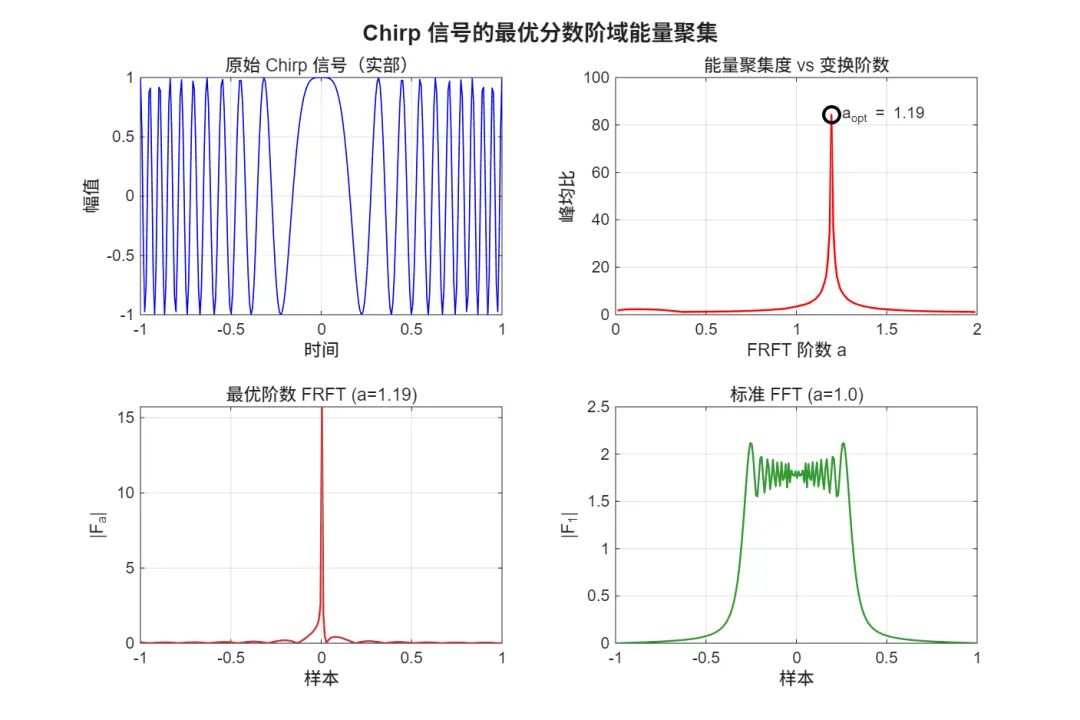
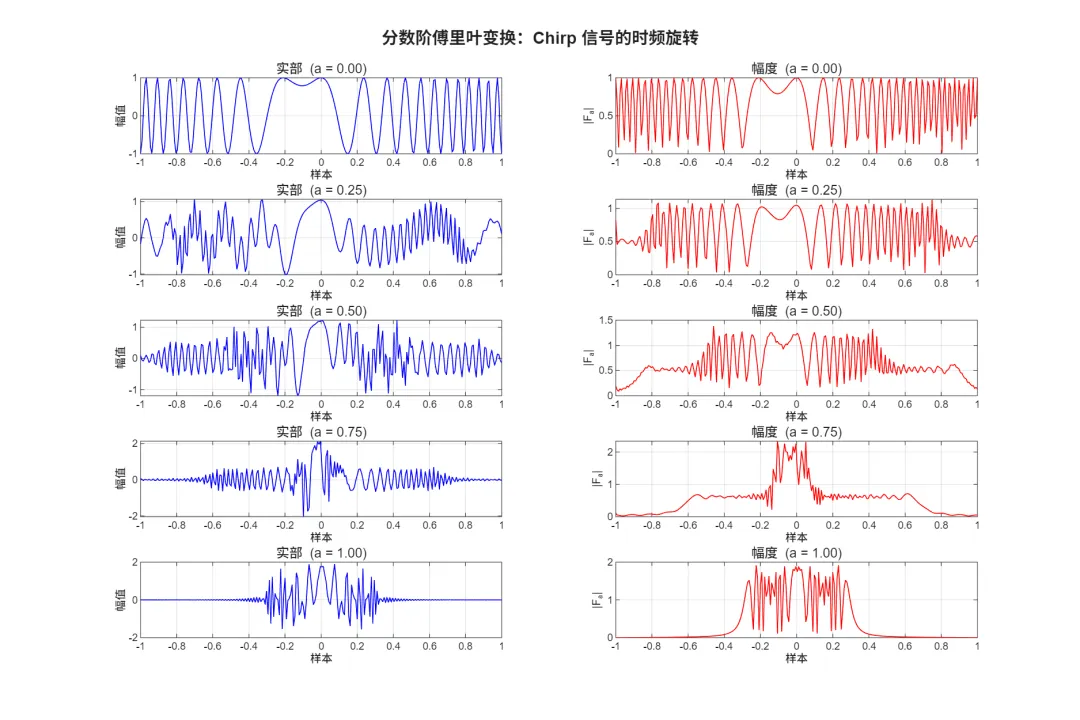
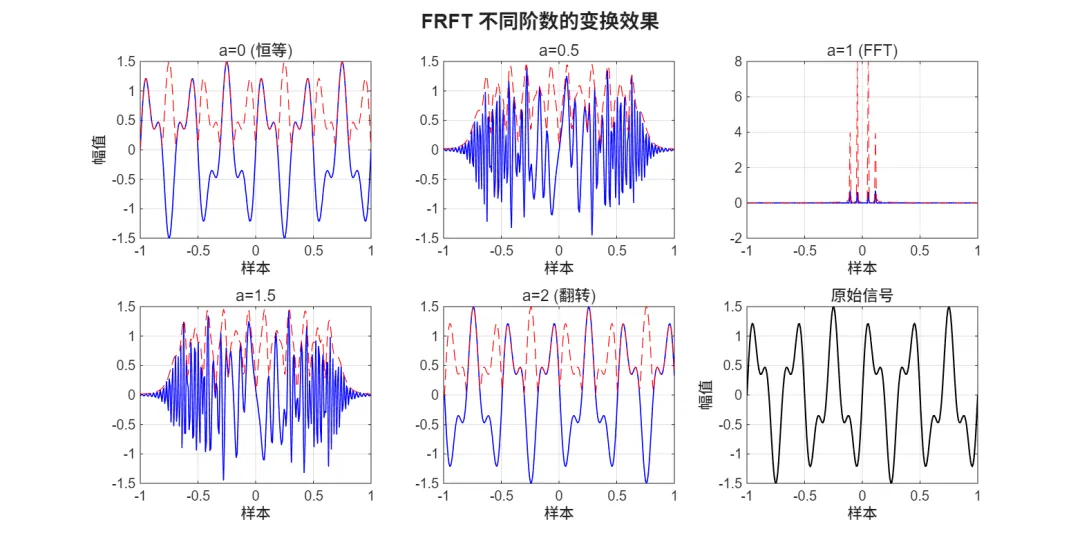
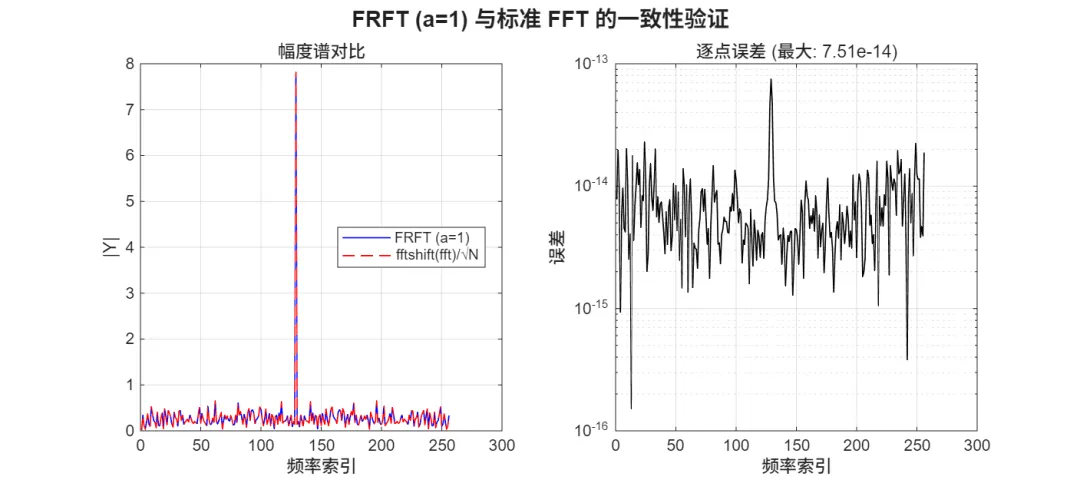
🖥️ 运行环境

📁 代码规模（当前工程）

• 20 个 .m 文件
• 约 812 行 MATLAB 代码
• 文档体系：算法文档.md + 代码文档.md + 项目文档.md

✅ 您将获得

🛒 获取方式