2026国省考:数学运算的15个技巧(PDF下载)

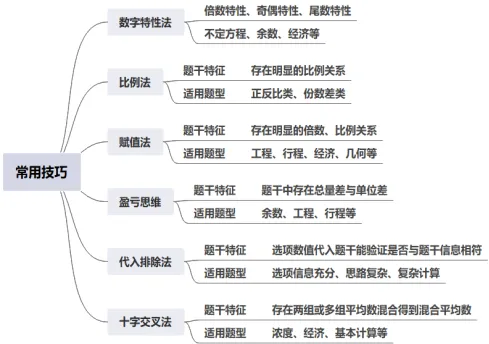
数学运算的解题技巧主要可以归纳出6条:
如果你比较急
可在我置顶朋友圈下载PDF

往期推荐:

【完整电子版讲义】可到文末找我领取。
第一百零四卷:代入排除法
代入排除法:将选项中数值代入到题干中进行验证,符合题干信息即正确选项,不符合即为错误选项的一种方法。
【母题训练】
某学校要将全体运动员排成方阵,老师按人数粗略估计进行第一次排列,发现多出99人,于是又将每行和每列多加了4人进行排列,发现缺少37人。问学校共有运动员多少人?
A.256 B.289 C.324 D.361
【解析】由于第一次成方阵之后多99个人,故总人数-99=平方数,此时可将选项中的总人数依次代入验证:
A项,256-99=157不是个平方数,排除;B项,289-99=190不是平方数,排除;C项,324-99=225=15²,符合题意;D项,361-99=262不是平方数,排除。故答案为C。
【子题训练】
1.春节期间,省图书馆邀请多位书法老师免费为读者书写春联。现场书写的春联中有188幅不是A老师书写的,有219幅不是B老师书写的,A、B两位老师今年一共书写了311幅春联。 问B老师今年一共书写了多少幅春联?
A.208B.171C.140D.126
2.四人年龄为相邻的自然数列且最年长者不超过30岁,四人年龄之乘积能被2700整除且不能被81整除。则四人中最年长者多少岁?
A. 30B. 29C. 28D. 27
3.某单位员工集中核酸检测,18人一组混检,需m(m为正整数)个组,但会多余1人,如果分成m-1个组,人数刚好平均分配。问该单位有多少员工?
A. 325B. 361C. 415D. 469
4.某宣传部门为喜迎伟大祖国70华诞,特组织n名来自全国各地的党员进行一次红色革命之旅的拓展活动。已知每名参加活动的党员在活动前都互相不认识,且在活动中最少与除自己以外的另1名党员互相认识。问至少能找到多少名党员,他们在活动中新认识的人数相同?
A.2B.3C.4D.n/2
5.某种设备的采购费用为5600万元,第一个月的维护费用为10万元,往后每个月的维护费用都比上个月高20万元。问企业如只能在每月初采购新设备,要使得连续使用过程中的总体使用成本最低,新设备的更换周期应为多少个月?
A. 24B. 26C. 28D. 30
第一百零五卷:数字特性法
数字特性法:一种通过数字之间的倍数关系、奇偶性质、尾数判断这几种方法来加速解题或秒杀破题的一种方法。
常用的三类题:母题系列、不定方程类、总量为“n多”类
【母题训练】
甲乙丙丁四人一起去踏青,甲带的钱是另外三个人总和的一半,乙带的钱是另外三个人的三分之一,丙带的钱是另外三个人的四分之一,丁带了91元,他们一共带了____元。
A.364 B.380 C.420 D.495
【解析】由于甲带的钱是另外三个人总和的一半,那么乙+丙+丁=2甲,四人钱数之和=3甲,即总钱数是3的倍数,排除AB;
由于乙的钱是另外三个人总和的三分之一,那么甲+丙+丁=3乙,四人钱数之和=4乙,即总钱数是4的倍数,排除D;故答案为C。
【子题训练】
1.某市对下辖9个文艺表演团体去年新创节目的数量进行统计分析,发现9个团体新创节目的数量恰好成等差数列,其中前5个团体的新创节目总数是60,前7个团体的新创节目总数是70。那么这9个文艺表演团体去年新创节目的总数是:
A.72 B.76 C.78 D.80
2.某公司三名销售人员2011年的销售业绩如下:甲的销售额是乙和丙销售额的1.5倍,甲和乙的销售是丙的销售额的5倍,已知乙的销售额是56万元,问甲的销售额是:
A.140万元 B.144万元 C.98万元 D.112万元
3.某人花400元购买了若干盒樱桃。已知甲、乙、丙三个品种的樱桃单价分别为28元/盒、32元/盒和33元/盒,问他最多购买了多少盒丙品种的樱桃?
A.3 B.4 C.5 D.6
4.甲乙两个班各有30多名学生,甲班男女生比为5∶6,乙班男女生比为5∶4,问甲、乙两班男生总数比女生总数:
A.多1人 B.少1人 C.多2人 D.少2人
5.高校某专业70多名毕业生中,有96%在毕业后去西部省区支援国家建设。其中去偏远中小学支教的毕业生占该专业毕业生总数的20%,比任职大学生村官的毕业生少2人,比在西部地区参军入伍的毕业生多1人,其余的毕业生选择去国有企业西部边远岗位工作。问去国有企业西部边远岗位工作的毕业生有多少人?
A.32 B.29 C.26 D.23
第一百零六卷:比例法
比例法:根据两个或多个数值之间的比例关系,与题干给定的具体值,来推算各项数值的比例关系或者具体数值大小。
【母题训练】
三个游泳运动员一起练习,当甲游1圈时,乙正好超过甲半圈,丙超过甲1/4圈,按此速度三人共游了15圈。问丙游了多少圈?
A.7圈 B.6圈 C.5圈 D.4圈
【解析】由于当甲游1圈时,乙游了1.5圈,丙游了1.25圈,根据路程=时间×速度,当时间相同时,速度之比等于路程之比,可得三者速度比为:甲:乙:丙=1:1.5:1.25=4:6:5。当三人共游了15圈时,根据时间相同,路程之比等于速度之比,则丙游的路程在4+6+5=15份中占5份,因此丙游了15×5/15=5圈。故本题答案为C。
【子题训练】
1.甲、乙、丙三人加工一种零件,三人每小时一共可以加工70个零件。如果甲乙两人每小时加工的零件数之比为2:3,乙丙两人每小时加工的零件数之比为4:5,则丙每小时比甲多加工( )个零件。
A.8B.10C.14D.16
2.甲、乙两人用相同工作时间共生产了484个零件,已知生产1个零件甲需5分钟、乙需6分钟,则甲比乙多生产的零件数是( )。
A.40个B.44个C.45个D.46个
3.甲乙二人沿环形跑道从同一地点同时背向开始跑步,35秒后两人相遇。已知甲跑一圈需要60秒,乙跑一圈需要多少秒?
A.77 B.84 C.91 D.96
第一百零七卷:赋值法
赋值法:为了方便计算,将题干中未知的数值,根据比值或倍数关系,赋上具体的数值来加速计算的一种方法,使用前提是“所赋数值的大小不影响实际结果”。
【母题训练】
高架桥12:00~14:00每分钟车流量比9:00~11:00少20%,9:00~11:00.12:00~14:00.17:00~19:00三个时间段的平均每分钟车流量比9:00~11:00多10%。问17:00~19:00每分钟的车流量比9:00~11:00多:
A.20% B.30% C.40% D.50%
【解析】观察题干,均是倍数关系,无具体数值,考虑使用赋值法。
由于12:00~14:00每分钟车流量比9:00~11:00少20%,则赋值9:00~11:00每分钟车流量为10,12:00~14:00每分钟车流量为10×(1-20%)=8;由于9:00~11:00.12:00~14:00.17:00~19:00三个时间段的平均每分钟车流量比9:00~11:00多10%,则三个时间段的平均车流量为10×(1+10%)=11,所以17:00~19:00每分钟车流量为11×3-10-8=15,那么17:00~19:00每分钟的车流量比9:00~11:00多(15-10)/10=50%,故本题答案为D。
【子题训练】
1.某企业四月的营业额比三月的营业额多三分之一,五月的营业额比四月多三分之一,则三月的营业额比五月的营业额少:
A.1/6 B.2/3 C.7/9 D.7/16
2.甲施工队每天能完成某项工程的1/9,乙施工队施工效率是甲施工队的两倍,则甲、乙两队同时施工( )天就能完成该工程。
A.2B.3C.4D.5
3.某医疗器械公司为完成一批口罩订单生产任务,先期投产了A和B两条生产线,A和B的工作效率之比是2:3,计划8天可完成订单生产任务。两天后公司又投产了生产线C,A和C的工作效率之比为2:1。问该批口罩订单任务将提前几天完成?
A.1 B.2 C.3 D.4
4.某智能设备满电情况下不接外部电源,可以开机使用3小时或者待机51小时,现在满电且不接外部电源情况下,开机使用N分钟后,剩余电量的待机时长也是N分钟,问N是多少?
A.140B.150C.160D.170
5.某商店购进一批篮球,定价为进价的125%,在售出进货量的20%后,商店决定打折促销。篮球全部卖完后,商家在该批篮球上总获利15%,问该商店这次促销价为定价的多少折?
A.8 B.8.5 C.9 D.9.5
二、数学运算高频考点概要
数学运算的常规考点包括高频和低频两类。高频考点,属于近5年国、省考基本每年都有考查的知识点,主要包括:基本计算、工程、行程、经济利润、最值、几何、排列组合、概率问题这八大考点。低频考点,为近5年国、省考偶考的知识点,主要有:容斥原理、周期日期、鸡兔同笼、植树问题等。
第一百零八卷:基本计算问题
一、基本计算问题
根据题意,进行基本的加减乘除类的运算,或通过列方程直接解题的题目都可以看做是基本计算问题。而涉及常用的基本公式或解题思路的,则再统一归类为某类考点,比如工程问题、行程问题等。
二、不定方程题
不定方程:主要指“未知数个数”大于“方程个数”的题。比如根据题意可得2个方程,但其中却存在3个未知数,则为不定方程题。
不定方程的计算思维:数字特性中的倍数特性、奇偶性、尾数特性等。
三、等差、等比类题
等差数列的基本公式:
第n项:(d为公差)
n项的和:
等比数列的基本公式:
第n项:(q为公比)
n项的和:
【母题训练】
某方舱医院配有1000张床位,现已接收新冠确诊患者200名,并按床护比(护士数与床位数的比值)0.6:1配齐了护士人员。因疫情发展迅速,该医院又收治了700名患者,此时床护比下调为0.2:1,那么还需增加护士:
A.80人 B.60人 C.40人 D.20人
【解析】由于最初接收患者200名,床护比为0.6:1,根据一个床位一名患者,故护士数:患者数=0.6:1,所以医院有护士200×0.6=120名。
增加了700名患者后,患者有200+700=900人,床护比下调为0.2:1,此时需要护士900×0.2=180人,则还需增加护士180-120=60人,故本题答案为B。
【子题训练】
1.某部门正在准备会议材料,共有153份相同的文件,需要装到大小两种文件袋里送至会场,大的每个能装24份文件,小的每个能装15份文件。如果要使每个文件袋都正好装满,则需要大文件袋( )个。
A.2 B.3 C.5 D.7
2.某次田径运动会中,选手参加各单项比赛计入所在团体总分的规则为:一等奖得9分,二等奖得5分,三等奖得2分。甲队共有10位选手参赛,均获奖。现知甲队最后总分为61分,问该队最多有几位选手获得一等奖?
A.3 B.4 C.5 D.6
3.幼儿园需采购春联、窗花、小狗玩偶三种新年用品,已知大班采购春联7幅,窗花12对、小狗玩偶5个,共花费200元,中班采购对联9幅、窗花19对、小狗玩偶5个,共花费224元。问小班采购春联10幅,窗花10对,小狗玩偶10个需花费多少元?
A.170 B.176 C.340 D.352
4.某市举行庆典活动,将依次升空105架无人机,升空方式如下:每架无人机间距均相等,第一次升空n架,第二次升空n-1架,以此类推,最终在夜空中组成一个近似等边三角形背景的灯光秀,那么第10次升空的无人机数量是:A.3架 B.5架 C.8架 D.10架
第一百零九卷:经济利润问题
一、基础公式
利润=售价-成本
总销售额=销售单价×销量、总成本=单个成本×销量
总利润=单个利润×销量=总收入-总成本
二、分段计费型题
第①步:分段计算各阶段费用
第②步:汇总求和
【母题训练】
某市针对虚假促销的专项检查中,发现某商场将一套茶具加价4成再以8折出售,实际售价比原价还高24元,问这套茶具的原价是多少元?
A.100 B.150 C.200 D.250
【解析】设茶具原价为x元,加价4成后的价格为x×(1+40%)=1.4x,再打8折后的售价为1.4x×0.8=1.12x元,实际售价比原价高24元,即:1.12x-x=24,解得:x=200元,故答案为C。
【子题训练】
1.某仓库有一批货物以75%的利润率出售,售出90%后,剩下的货物全部以6折出售,那么这批货物的最终利润率为∶
A.68% B.62% C.54% D.51%
2.某种蔬菜进价5元/斤,售价10元/斤,当天卖不完的蔬菜不再出售。过去7天里,菜商每天购进该种蔬菜100斤,其中有4天卖完,有2天各剩余20斤,有1天剩余10斤,这7天菜商共赚了多少元钱?
A.2950 B.3000 C.3250 D.3500
3.假设个人出版著作所得稿费纳税方法如下:(1)稿费不超过800元不纳税;(2)超过800元但不超过4000元的部分纳税10%;(3)超过4000元的部分纳税15%。已知张教授出版一部著作,纳税620元,则张教授的这笔稿费是多少元?
A.9000 B.8000 C.7000 D.6000
4.某商场做促销活动,一次性购物不超过500元的打九折优惠;超过500元的,其中500元打九折优惠,超过500元部分打八折优惠。小张购买的商品需付款490元,小李购买的商品比原价优惠了120元。如两人一起结账,比分别结账可节省多少元钱?
A.10 B.20 C.30 D.50
第一百一十卷:工程问题
一、基本公式:
工作总量=工作效率×工作时间
总量相同,效率和时间呈反比;
时间(效率)相同,总量和效率(时间)呈正比;
二、工程问题的3种类型
1、完工时间型
①赋值总量为几个完工时间的公倍数 ②分别计算效率 ③计算其他
常考出题类型:同时合作、先后合作、中途退出、提前/延期、交替合作型等
2、效率比型
①按照比例赋值效率 ②计算总量 ③计算其他
3、具体值型
①根据题意设未知数 ②找等量关系列方程
注意:题干中存在多个相同主体时,可考虑赋值其效率为1
【母题训练】
一项工程由甲、乙工程队单独完成,分别需50天和80天。若甲、乙工程队合作20天后,剩余工程量由乙、丙工程队合作需12天完成,则丙工程队单独完成此项工程所需的时间是( )。
A.40天 B.45天 C.50天 D.60天
【解析】由于甲、乙单独完成分别需要50天和80天,故赋值工程总量为50和80的公倍数400,则甲的效率为400/50=8,乙的效率为400/80=5。甲、乙合作20天后,剩余的工程量为400-20×(8+5)=140,乙、丙合作12天能完成剩余工作量,故乙、丙的效率之和为140/12=35/3,丙的效率为35/3-5=20/3。若由丙单独完成整项工程,需要的时间为400÷20/3=60天,故答案为D。
【子题训练】
1.甲和乙两个小组共同植树,计划共同花10个小时完成,但实际上甲组先单独开工,2小时后乙组加入,又过1个小时后还剩3/4没有完成,已知甲组比乙组每个小时多植树10棵,问两个小组一共要植多少棵?
A.200 B.220 C.240 D.300
2.某单位办事大厅有3个相同的办事窗口,2天最多可以办理600笔业务,每个窗口办理单笔业务的用时均相同。现对该办事大厅进行流程优化,增设2个与以前相同的办事窗口,且每个办事窗口办理每笔业务的用时缩短到以前的2/3。问优化后的办事大厅办理6000笔业务最少需要多少天?
A.8 B.10 C.12 D.15
3.社区居委会张阿姨为表达对志愿者的感谢,买了一些毛线,准备织帽子和手套。这些毛线如果全部织帽子可织15个,全部织手套可织20只,现将一个帽子和两只手套做成一个“爱心礼包”。这些毛线最多可做成几个“爱心礼包”?
A.4 B.5 C.6 D.7
4.某单位甲、乙、丙三人负责整理一项档案,他们工作5天完成了1/4,之后甲和乙因其他工作被调离,两天后才返回,期间丙继续整理档案。已知甲、乙、丙三人的工作效率之比为4∶3∶2,则完成这项工作共需要花费( )天。
A.20 B.21 C.22 D.23
第一百一十一卷:行程问题
一、基础公式
路程=速度×时间
等时间平均速度=
等距离平均速度=
二、正反比关系
路程相同,速度和时间呈反比;
时间(速度)相同,路程和速度(时间)呈正比;
三、直线上追及、相遇公式
追及问题:追及距离=(大速度-小速度)×追及时间相遇问题:相遇距离=(大速度+小速度)×相遇时间背离问题:背离距离=(大速度+小速度)×背离时间
四、环形上追及、相遇公式
反向出发:
第n次相遇路程和为n个周长,环形周长=(大速度+小速度)×相遇时间同向出发:
第n次相遇路程差为n个周长,环形周长=(大速度-小速度)×相遇时间
五、往返相遇中,路程和与全程的关系两端出发:第N次迎面相遇,路程和=全程×(2n-1)第N次追上相遇,路程差=全程×(2n-1)同一点出发:第n次迎面相遇,路程和=全程×2n第n次追上相遇,路程差=全程×2n
【母题训练】
老李每天早晨9点准时出门散步锻炼身体。他以3千米每小时的速度步行6千米,其中每走20分钟休息5分钟。那么老李锻炼到( )回家。
A.11点20分 B.11点25分 C.11点30分 D.11点45分
【解析】由于老李每走20分钟休息5分钟,且每20分钟走的路程为:3×20/60=1千米,故老李步行6公里需要的时间为20×6/1=120分钟,中间需要休息5次,休息花费的时间为:5×5=25分钟,因此所需要的总时间为120+25=145分钟=2小时25分钟,即老李锻炼到11点25分回家,故本题答案为B。
【子题训练】
1.汽车在平直的公路上运动,它先以速度V行驶了2/5的路程,接着以30km/h的速度驶完余下的3/5路程,若全程平均速度是40km/h,则V是多少?
A.60km/h B.70km/h C.80km/h D.90km/h
2.科研人员在山路测试救援机器人性能。已知救援机器人电池续航时间为60分钟,其上坡、下坡、平路速度分别为4米/秒、8米/秒、6米/秒。机器人从A点出发,沿箭头所示路线行进一定距离后折返,并在电量耗尽时正好返回A点。问机器人在折返前最多能行进多少米?
A.6750 B.10350 C.13500 D.17100
3.寒假第一天,骑行社团从学校出发去滑雪,他们以20公里/小时的速度骑行2个小时到达滑雪场,游玩4个小时后按原路以原速返回。骑行社团离开学校5.5小时后,辅导员派大客车以40公里/小时的速度沿相同路线迎接骑行社团,则大客车出发后与骑行社团相遇需要的时长是:
A.30分钟 B.40分钟 C.50分钟 D.60分钟
4.某圆形跑道长为400米,甲从跑道上A点以6米/秒的速度顺时针跑步前行。乙在A点对应直径的另一端B点同时以5米/秒的速度逆时针跑步前行,问在14分钟内,他们共相遇了多少次?
A.22 B.23 C.24 D.25
5.某宣讲团甲宣传员骑摩托车从红星村出发以20公里/小时的速度去相距60公里的八一村,1小时后由于路面湿滑,速度减少一半,在甲出发1小时后,乙宣传员以50公里/小时的速度开车从红星村出发追甲,当乙追上甲时,他们与八一村的距离为:
A.25公里 B.30公里 C.35公里 D.40公里
第一百一十二卷:排列组合问题
一、基本概念
排列组合是组合学最基本的概念。所谓排列,就是指从给定个数的元素中取出指定个数的元素进行排序。组合则是指从给定个数的元素中仅仅取出指定个数的元素,不考虑排序。
二、基本公式
三、两个原理
①分类原理:分类考虑用加法,各个类别的情况数相加等于总情况数
常见关键词:要么…要么;至少…;至多…;等
②分步原理:分步用乘法,每步的情况数相乘等于总情况数
常见关键词:先…后… ;既…又…;且;以及;和;等
③分类和分步共存:分类中某类需要分步考虑;分步中某步需要分类考虑
【母题训练】
随着人们生活水平的提高,汽车拥有量迅速增长,汽车牌照号码需要扩容。某地级市交通管理部门出台了一种小型汽车牌照组成办法,每个汽车牌照后五位的要求必须是:前三位为阿拉伯数字,后两位为两个不重复的英文字母(字母O、I 不参与组牌),那么 用这种方法可以给该地区汽车上牌照的数量为:
A.397440辆 B.402400辆 C.552000辆 D.576000辆
【解析】本题求各种排列的情况总数,属于排列组合问题。一共5 位,其中前三位和数 字相关,后两位和字母相关,考虑分步处理。先安排前三位,每位都可以是 0-9 共 10 个数字中任一个 , 因此各有 C(10,1)种选法 ,前三位排法有 C(10,1)×C(10,1)× C(10,1)=1000 种;再安排后两位,英文字母共 26 个,字母 O、I 不参与组牌,剩 24 个, 由于这两个字母不重复,所以等于从 24 个字母中选出 2 个字母且要考虑顺序的情况数, 等于 A(24,2)=24×23=552 种。分步用乘法,因此可以给该地区汽车上牌照的数量为 1000 ×552=552000 辆。故答案为 C。
【子题训练】
1.某商场开展“助农销售”活动,凡购买某种农产品满300元者可获得一个礼盒,其中装有6种干货中的随机3种各1小袋,以及1袋小米或红豆。问内容不完全相同的礼盒共有多少种可能?
A.30 B.40 C.45 D.50
2.滑雪和滑冰是冬奥会的两大项赛事,其中高山滑雪、自由式滑雪、单板滑雪、跳台滑雪、越野滑雪和北欧两项是滑雪大项中的6个分项,短道速滑、速度滑冰和花样滑冰是滑冰大项中的3个分项。小林打算去现场观看比赛,共选择6个项目,并且每个大项不少于1个,若所有项目比赛时问均不交叉,则不同的观赛方式有:A.83种 B.84种 C.92种 D.102种
3.A、B、C三个社区需要建设若干个5G基站,三个社区可供选择的建设基站地点分别有2个、4个、5个,现从A、B、C三个社区分别选取1、2、3个地点随机分配给甲、乙、丙三个施工队进行建设,要求每个施工队只能承接一个社区,则承建方式有:
A.720种 B.480种 C.360种 D.120种
第一百一十三卷:概率问题
一、基本概念
概率,亦称“或然率”,它是反映随机事件出现的可能性大小。设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率为m/n。经过大量反复试验,m/n越来越接近于某个确定的常数(此论断证明详见伯努利大数定律)。该常数即为事件A出现的概率,常用P(A)表示。
二、基本公式
已知或计算得到:概率P(1)、P(2)、P(3)、…
分类概率:计算各类概率,最后求和。P(A)=P(1)+P(2)+P(3)+…
分步概率:计算各步概率,最后相乘。P(A)=P(1)×P(2)×P(3)×…
三、常见考法
·求概率、分类概率、分步概率、排列组合+概率
·反面求解:某事件发生的概率=1-该事件不发生的概率
·独立重复试验:
设在一次试验中,事件A发生的概率为p(0<p<1),则在n重独立重复试验中,事件A恰好发生 k 次的概率为:(k=0、1、2、…n)
设在一次试验中,事件A首次发生的概率为p(0<p<1),则在n重独立重复试验中,事件A在第 k 次试验中才首次发生的概率为:(k=0、1、2、…n)
【母题训练】
一个纸箱里装有大小及材质完全相同的10个小球,其中3个黑色,2个白色,1个红色,2个黄色,1个绿色,1个紫色。如果不放回地依次随机取出3个小球,则取出的小球依次是黑色、红色、白色的概率为:
A. 1/120B. 1/240C.1/250 D.3/500
【解析】概率=取出的小球依次是黑色、红色、白色的情况数/不放回地依次随机取出3个小球的情况数。
不放回地依次随机取出3个小球,第一步是从10个小球中随机选1个,有C(10,1)=10种选法;第二步从剩下的9个小球中随机选1个,有C(9,1)=9种选法;第三步从剩下的8个小球中随机选1个,有C(8,1)=8种选法;分步用乘法,共有10×9×8种。
取出的小球依次是黑色、红色、白色的情况数,分步考虑,分别从3个黑球、1个红球、2个白球中取1个,可得情况数=C(3,1)×C(1,1)×C(2,1)=3×1×2。
所求概率=(3×1×2)/(10×9×8)=1/120。故答案为A。
【子题训练】
1.甲乙两人相约骑共享单车运动健身。停车点现有9辆单车,分属3个品牌,各有2、3、4辆。假如两人选择每一辆单车的概率相同,两人选到同一品牌单车的概率约为:
A.1/6 B.2/9C.5/18 D.1/3
2.一个桶中有红球、白球共30只,这些球除颜色外都相同,将桶中的球搅拌均匀,从中随机摸出一只球,记下它的颜色后再放回,不断重复这一过程,共摸了60次,发现有20次摸到红球,问这个桶中大约有多少只红球?A.8 B.10 C.12 D.20
3.甲、乙、丙、丁四个车间生产相同的产品,生产效率之比为4:3:2:1,产品不合格率分别为2%、3%、4%、5%。质检人员从这4个车间某小时内生产的所有产品中随机抽取1件,发现该产品不合格,该产品是乙车间生产的概率为( )。
A.30% B.40% C.50% D.60%
4.小张回家乘地铁18:45之前到家的概率为0.8,乘公交为0.7。已知小张下班回家要么乘地铁,要么乘公交,且选择乘地铁的概率为0.6,则他下班回家18:45之前到家的概率是:
A. 0.73B. 0.74C. 0.75D. 0.76
5.天气预报对未来五天的天气情况进行了预测,每天晴天的概率都是0.7,不晴天的概率是0.3。那么这5天中恰好3天睛天的概率的是多少?
A. 0.031B. 0.343C. 0.185D. 0.309
第一百一十四卷:最值问题
最值思维:就是“极端思维”,根据题意分析最极端的情况,可能是最优情况,也可能是最不利的情况。
运用最值思维的两类题:
最不利构造题:
题干特征:至少……保证……(求最大或最小值)
解题思路:最不利情况+1
构造数列题:
题干特征:已知总值和几个元素间关系,求最大或最小值
常见类型:多个元素的值各不相同、多个相同等
解题思路:①设未知数,构造数列;②列式计算:加和=总值
【母题训练】
已知某宾馆共有30个房间,一名清洁工拿着30把钥匙,他只知道一把钥匙开一把锁,但是不知道哪把钥匙开哪把锁,现在她要打扫每一间房子,需要将钥匙和房间一一匹配,她最多要试多少次?
A.365 B.385 C.435 D.465
【解析】由于总共有30个房间,所有钥匙都是打乱的,则第1把钥匙最多要试29次(第29个房间也打不开,则一定是第30个房间),第2把钥匙要从剩余29个房间试,最多试28次,同理可得:第3把钥匙最多要试27次、第四把钥匙最多要试26次…第29把钥匙要试1次,第30把只剩最后一个房间,不用试。
故所试的次数刚好为公差为1的等差数列,根据等差数列求和公式:Sn=(a1+an)×n/2,故清洁工最多要试29+28+27+…+3+2+1=(1+29)×29/2=435次。故本题答案为C。
【子题训练】
1.某集团有13个分公司,每个分公司的员工数均不超过50人。甲和乙两个分公司各招聘若干人后,员工人数分别达到76人和137人,且集团平均每个分公司的员工数增加了9人。问甲分公司和乙分公司在招聘前的员工数最多相差几人?
A.4 B.3 C.2 D.1
2.某地区招聘卫生人才,共接到600份不同求职者的简历。其中,临床、口腔、公共卫生和护理专业分别有200人、160人、140人和100人,问至少有多少人被录用,才能保证一定有140名被录用者专业相同?
A.141 B.240 C.379 D.518
3.从某物流园区开出6辆货车,这6辆货车的平均装货量为62吨,已知每辆货车载重量各不相同且均为整数,最重的装载了71吨,最轻的装载了54吨。问这6辆货车中装货第三重的卡车至少装载了多少吨?
A.59B.60C.61D.62
4.某单位A、B、C三个库房各存放若干台电脑,已知A 库房比B库房多4台,B库房比C库房多2台,C库房和A库房共22台。如果将所有电脑发放给单位的不同部门,要求每个部门获得的电脑数量均不相同,问最多可以发放给几个部门?A.6 B.7 C.8 D.9
第一百一十五卷:几何问题
一、基本公式
二、两类题
①最短距离:两点之间线段最短
②解直角三角形:勾股定理()
等腰直角三角形:
90°、60°、30°的直角三角形:
特殊勾股数:3、4、5;5、12、13;6、8、10;8、15、17等
【母题训练】
部队前哨站的雷达监测范围为100千米。某日前哨站侦测到正东偏北30° 100千米处,一架可疑无人机正匀速向正西方向飞行。前哨站通知正南方向150千米处的部队立即向正北方向发射无人机拦截,匀速飞行一段时间后,正好在某点与可疑无人机相遇。问我方无人机速度是可疑无人机的多少倍?
【解析】如图所示,前哨站(O点)在A点发现可疑无人机,可疑无人机从A点向西飞行(即AB方向),我方无人机从C点向北飞行并最终在B点与可疑无人机相遇,那么可疑无人机行驶的路程为AB,我方无人机行驶的路程为BC。
在Rt△ABO中,∠A=30°,OA=100千米,可得:OB=AO×(1/2)=50,AB=OB=50而BC=BO+OC=50+150=200。时间相同,路程之比等于速度之比,则我方无人机的速度为可疑无人机的倍,故答案为B。
【子题训练】
1.某商场为庆祝开业三周年,制作了一个长方形大蛋糕,并切成四块,如图所示。假设这个蛋糕可共350人享用,左下角那块蛋糕平均可共50人享用,右上角那块蛋糕平均可共70人,则中间最大块蛋糕平均可供多少人享用?A.150 B.155 C.175 D.180
2.悟空与二郎神在离地面1米的空中决斗,两人相距2米,悟空想用分身直接偷袭二郎神,为了不引起对方的警觉,分身必须在地面反弹一次再进行攻击,则分身到达二郎神的位置所走的最短距离为:
3.兔子和乌龟举行一场跑步比赛,终点位于起点正北方500米位置。兔子的速度是乌龟的5倍,兔子和乌龟同时出发,兔子先向正东方跑了一会儿后意识到自己方向错误,马上直奔终点,速度不变,结果兔子和乌龟同时到达。问兔子意识到自己的错误时已经跑了多少米?A.600 B.1200 C.2400 D.3000
4.一艘非法渔船作业时发现其正右方有海上执法船,于是沿下图所示方向左转30°后,立即以15节(1节=1海里/小时)的速度逃跑,同时执法船沿某一直线方向匀速追赶,并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时与执法船的距离相同,问执法船的速度为多少节?
第一百一十六卷:容斥原理
一、基本公式
1.二集合
A∪B=A+B-A∩B
A∪B=只满足一个条件的+同时满足两个条件的
A∪B=总数-两个条件都不满足的
2.三集合
A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C
A∪B∪C=只满足一个条件的+只同时满足两个条件的+同时满足三个条件的
A∪B∪C=满足一个条件的-只同时满足两个条件的-2×同时满足三个条件的
A∪B∪C=总数-三个条件都不满足的
二、解题方法
公式法、图示法
【母题训练】
某班有60人,参加物理竞赛的有30人,参加数学竞赛的有32人,两科都没有参加的有20人。同时参加物理、数学两科竞赛的有多少人?
A.28人 B.26人 C.24人 D.22人
【解析】由于参加物理的有30人,数学竞赛有32人,两科都未参加的有20人,总人数有60人,故本题考查二集合容斥原理。
根据二集合容斥原理可得:总人数-都未参加的人数=参加数学的人数+参加物理的人数-同时参加两科的人数,则60-20=32+30-同时参加两科的人数,同时参加两科的人数=62-40=22人,故本题答案为D。
【子题训练】
1.学校有300个学生选择参加地理兴趣小组,生物兴趣小组或者两个小组同时参加。如果80%学生参加地理兴趣小组,50%学生参加生物兴趣小组。问同时参加地理和生物兴趣小组的学生人数是多少?
A.240 B.150 C.90 D.60
2.某单位共有240名员工,其中订阅A期刊的有125人,订阅B期刊的有126人,订阅C期刊的有135人,订阅A、B期刊的有57人,订阅A、C期刊的有73人,订阅3种期刊的有31人,此外,还有17人没有订阅这三种期刊中的任何一种。问订阅B、C期刊的有多少人?
A.57 B.64 C.69 D.78
3.甲、乙两个单位分别有60和42名职工,共同成立A、B两个业余活动小组,所有职工每人至少参加1个。乙单位职工中仅参加A组的人数是只参加一个小组人数的60%,乙单位职工中参加B组的人数与参加A组的人数之比为3∶4,参加B组的人中,甲单位职工占5/8。问有多少人仅参加A组?
A.35 B.42 C.46 D.56
4.为实现产业振兴,农科院对某县的所有自然村进行了调研,结果发现,适合种植A作物的自然村占4/13。适合种植B作物的自然村有25个,同时适合种植两种作物的自然村占总数的1/14,则在该县不适合种植两种作物的自然村至少有多少个?
A.57 B.67 C.114 D.134
第一百一十七卷:日期问题
一、星期推断型
题目特征:已知日期和星期几,推断另一个日期是星期几
解题思路:总天数/7=a……b(余数b为几,星期加几)
二、日期推断型
题目特征:已知日期和天数,推断下一个日期
常见解题方式:总天数/30,按月份填补
三、注意事项
1. 大月(1、3、5、7、8、10、12月)31天,小月(4、6、9、11月)30天
2. 平年:2月28天,全年365天;闰年:2月29天,全年366天
3. 闰年判断方式:能被400整除,或能被4整除但不能被100整除的是闰年。
4.“每n天”的周期为n天,“每隔n天”的周期是n+1天
【母题训练】
已知2021年7月1日星期四,那么2021年12月10日是星期几?
A.星期二 B.星期三 C.星期四 D.星期五
【解析】由于2021年7月2日至2021年12月10日总共有30+31+30+31+30+10=162天,一周有7天,则162/7=23…1天,2021年7月1日往后经过了23个完整的星期还是星期四,再过一天就到了2021年12月10日,刚好为星期五,故本题答案为D。
【子题训练】
1.甲乙丙三个志愿者共同照顾李奶奶,甲每4天去一次,乙每5天去一次,丙每6天去一次。如果他们三个于5月5日在李奶奶家同时见面,则他们三人下次在李奶奶家同时见面的时间是:
A.7月4日 B.7月5日 C.9月1日 D.9月2日
2.甲、乙、丙三人都报名去摄影馆学习摄影技术,甲每隔4天去一次,乙每隔5天去一次,丙每隔6天去一次,三人在星期四第一次相遇,下次相遇的日期为∶
A.星期一 B.星期三 C.星期四 D.星期五
3.某年的3月有5个星期一和4个星期二,则该年的国庆节是( )。
A.星期二 B.星期三 C.星期四 D.星期五
第一百一十八卷:浓度问题
基本公式:
溶液=溶质+溶剂
常用思路:赋值法、十字交叉法
【母题训练】
甲烧杯装有浓度为6%的酒精200克,乙烧杯装有浓度为10.5%的酒精100克。现向两个烧杯各加入x克水后,两个烧杯中酒精浓度相同。问x的值为:
A.350B.400C.550D.600
【解析】水是酒精这种溶液的溶剂,因此,根据“两个烧杯中酒精浓度相同”可知,两份溶液分别加入x克水后浓度相同,那么根据“浓度=溶质/溶液”可得等式:,解得x=600。故答案为D。
【子题训练】
1.现有一种浓度为15%的盐水30千克,如果用50千克浓度更高的盐水和它混合,混合后的盐水浓度将大于20%,而小于35%。据此可知,后加入的盐水的浓度(假设浓度为x)范围是:
A.23%<x<47%B.15%<x<35%
C.15%<x<23%D.23%<x<50%
2.有一瓶浓度为15%的盐水500克,每次加入34克浓度为60%的盐水,则至少加( )次该盐水,使这瓶盐水的浓度超过30%。
A.6B.7C.8D.9
3.一杯浓度为50%的糖水,加入一定量的水后浓度变为40%,再加入与上一次等量的水后,糖水变为60克,问糖水中的糖有多少克?
A.18B.20C.24D.30

【理论点拨】文字或是脑图,主要目的是帮助你快速梳理理论点。
【母题解构】基于考情趋势下最能反映考点或技巧精髓的试题。
【子题巩固】在对母题有效掌握的基础上,点对点、点对面的巩固训练。
理论学习+母题剖析+子题训练,更为扎实地搭建起整个知识框架体系。
【电子讲义PDF】
我已发在置顶朋友圈
添加我好友可直接下载

 夜雨聆风
夜雨聆风





