高三答案_2025年5月_0501河南省开封市2025届高三下学期第三次质量检测（全科）_河南省开封市2025届高三年级第三次质量检测数学试题

2025 届高三年级第三次质量检测 数学参考答案 注意事项：答案仅供参考，其他合理答案也可酌情给分。 一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要 求的。 题号 1 2 3 4 5 6 7 8 答案 A D D B B C C A 二、选择题：本题共3小题，每小题6分，共18分。在每小题给出的选项中，有多项符合题目要求。全部 选对的得6分，部分选对的得部分分，有选错的得0分。 题号 9 10 11 答案 BC AC ACD 三、填空题：本题共3小题，每小题5分，共15分。 2 12．1 13． 14．145 2 四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。 15.（13分） （1）由已知，得sin  AB  cosBcos  AB  sinB=0，即sin  A2B  =0，………3分 因为0 A，B，所以2 A2B， 所以A2B=0，或A2B=.………6分 （2）因为ab，所以AB，………7分  若A2B=，则A=2B0，B  A，所以A=2B，………8分 2 a sinA a sin2B a 2sinBcosB a 6 所以 =  =  = cosB= cosB= ，………11分 b sinB b sinB b sinB 2b 4 6 1 所以cosA=cos2B=2cos2 B1=2( )2 1 ………13分 4 4 16.（15分） （1）随机变量X 的所有可能取值为0，1，2，3．………1分 1 1 1 1 P(X 0)(1 )(1 )(1 ) ， 2 3 4 4 1 1 1 1 1 1 1 1 1 11 P(X 1) (1 )(1 )(1 ) (1 )(1 )(1 )  ， 2 3 4 2 3 4 2 3 4 24 1 1 1 1 1 1 1 1 1 1 P(X 2)(1 )   (1 )   (1 ) ， 2 3 4 2 3 4 2 3 4 4 1 1 1 1 P(X 3)    ， 2 3 4 24 所以，随机变量X 的分布列为 X 0 1 2 3 1 11 1 1 ………5分 P 4 24 4 24 1 11 1 1 13 随机变量X 的数学期望E(X)0 1 2 3  ．………7分 4 24 4 24 12 （2）记事件A为该棋手恰连胜两盘，则该棋手在第二盘一定为胜，设该棋手在第二盘与甲、乙、丙比赛且 1恰连胜两盘的概率分别为P ，P ，P ，则 甲 乙 丙 11 1 1 1 5 11 1 1 1 1 P 甲  A 2 2 2  3   1 4    4   1 3      12 ，P 乙  A 2 2 3  2   1 4    4   1 2     = 3 ， 11 1 1 1 1 P 丙  A 2 2 4  2   1 3    3   1 2      4 ，………13分 5 1 1 因为   ，所以P P P ，………14分 甲 乙 丙 12 3 4 所以P 最大，即棋手在第二盘与甲比赛恰连赢两盘的概率最大．………15分 甲 17.（15分） （1） f(x)ex x2+2ax+a1  ，………1分 方程x2+2ax+a10的=2a2 +4a1=a2 0，………2分 所以方程x2+2ax+a10有解，即方程ex x2+2ax+a1  =0有解，………3分   所以 f x 存在斜率为0的切线.………4分 （2）解方程x2+2ax+a10，得x1或x=1a，………5分 ①a=0时， f(x)0， f  x  单调递减，无极值；………6分 ②a0时，由 f(x)0，得1x1a，由 f(x)0，得x1或x1a，………7分 所以 f  x  在  1，1a  上单调递增，在 ，1 ， 1a，+ 上单调递减，………8分 极小值为 f 1e1a2，由 f  1 0得a2；………10分 ③a0时，由 f(x)0，得1ax1，由 f(x)0，得x1a或x1，………11分 所以 f  x  在  1a，1  上单调递增，在 ，1a ， 1，+ 上单调递减，………12分 极小值为 f 1aea12a，由 f  1a 0得a2，………14分 综上所述，a的取值范围为 ，2    2，+ .………15分 18.（17分） （1）证明：连接AC ，BC ，在ABC 中，E，F 分别是AB，AC的中点，所以EF∥BC ， 1 1 1 1 1 因为AC  EF，所以AC  BC ，………1分 1 直三棱柱ABCABC 中，AC CC ，………2分 1 1 1 1 又CC BC =C ，CC、BC 平面BCC B ，所以AC 平面BCC B ，………3分 1 1 1 1 1 1 1 1 1 又BC 平面BCC B ，所以AC  BC .………4分 1 1 （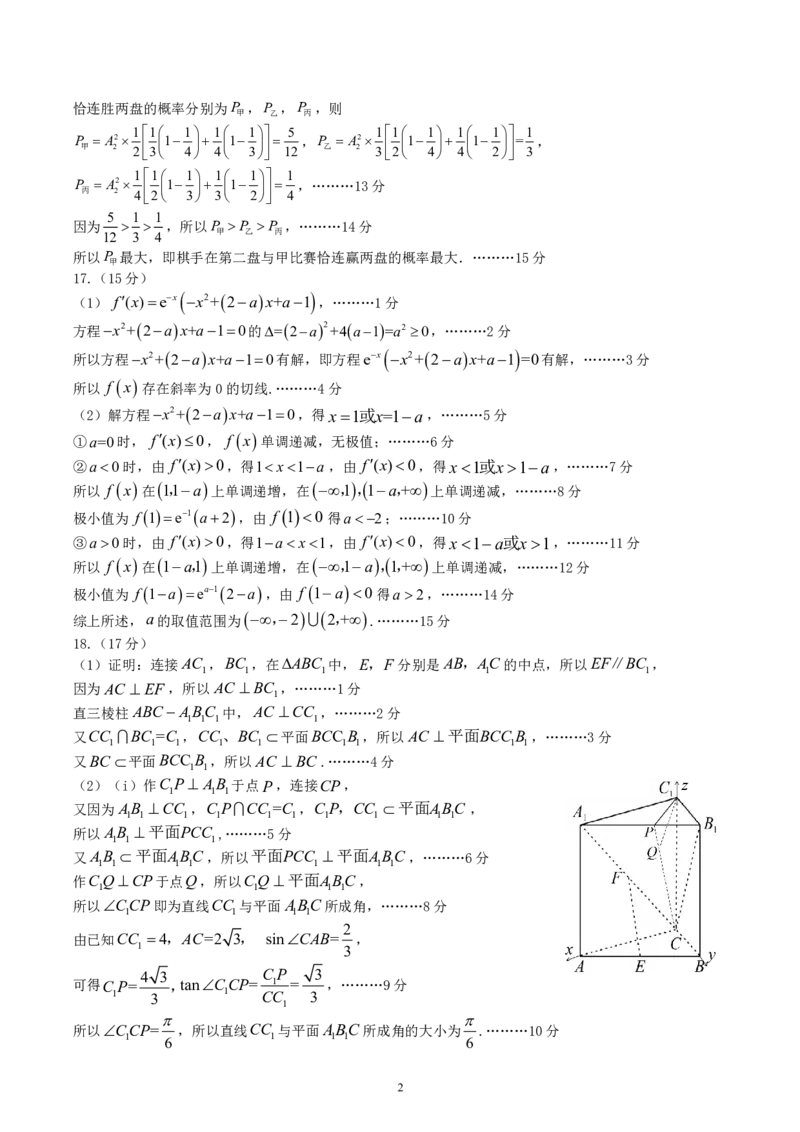2）（i）作C P  AB 于点P，连接CP， 1 1 1 又因为AB CC ，C PCC =C ，C P，CC 平面ABC ， 1 1 1 1 1 1 1 1 1 1 所以AB 平面PCC ,………5分 1 1 1 又AB 平面ABC，所以平面PCC 平面ABC，………6分 1 1 1 1 1 1 1 作CQ CP于点Q，所以CQ 平面ABC， 1 1 1 1 所以CCP即为直线CC 与平面ABC所成角，………8分 1 1 1 1 2 由已知CC 4，AC=2 3， sinCAB= ， 1 3 4 3 C P 3 可得C P= ，tanCCP= 1 = ，………9分 1 3 1 CC 3 1   所以CCP= ，所以直线CC 与平面ABC所成角的大小为 .………10分 1 6 1 1 1 6 2   （ii）如图，分别以CA,CB,CC为x，y，z轴建立空间直角坐标系C-xyz………11分 1 过Q作QOCC 于O，由（i）易得QO 3，OC 3， 1 所以旋转过程中Q在以O为圆心，以 3为半径的圆周上，且圆O所在平面垂直直线CC ，………12分 1 设Q  3cos, 3sin,3  其中 0,2 ，      因为A 2 3,0,0 ，所以AQ  3cos2 3, 3sin,3 ………13分  因为CC (0,0,4)， 1     AQCC 34 3 cos AQ,CC   1   所以 1 | AQ||CC |  2  2 2 2cos ……15分 1 4 3cos2 3  3sin 9   1 3 由于cos1,1  ，所以cos AQ,CC  , ………16分 1 2 2     所以直线AQ与直线CC 所成角的取值范围为 , .………17分 1  6 3   19.（17分） （1）当∠DOF=45°时，D坐标(2p，±2p)，………1分 p 因为|DF|=5，所以2p+ =5，即p=2，………2分 2 故抛物线C的方程是y2=4x．………3分 （2）（i）设P(a，b)，a<0，b<0，设A(x ，y )，B(x ，y )，直线PA方程：x－x =t(y－y )， 1 1 2 2 1 1 x－x =t(y－y )与y2=4x联立得y2－4ty+4ty －4x =0，………4分 1 1 1 1 因为PA是抛物线切线，所以△=16t2－16ty +16x =0， 1 1 y 又y 1 2=4x 1 ，所以t 1 ，故切线PA方程是yy 1 =2(x+x 1 )，………6分 2 同理切线PB方程是yy =2(x+x )．………7分 2 2 因为PA，PB均过点P(a，b)，所以by =2(a+x )且by =2(a+x )， 1 1 2 2 2 所以直线AB方程是by=2(a+x)，斜率是 ，………8分 b 2 b 因为直线PO与AB垂直，所以  1，故a=－2，………9分 b a 所以直线AB方程是by=2(x－2)，过定点Q(2，0)．………10分 （ii）由（1）知2p=4，由（i）知P(－2，b)，Q(2，0)， b b b b 故k   ，k   ， 1 2 2 2 22 4 n1 b 1 b 又数列{k n }是等比数列，所以k n  2   2    2n ，………11分 1 2n 设直线M N 的方程为x+2=t (y－b)，M (x ，y )，N (x ，y )，显然t   ． n n n n n1 n1 n n2 n2 n k b n 直线M N 的方程与抛物线C的方程联立得y²－4t y+4bt +8=0， n n n n 所以y +y =4t ，y y =4bt +8，△>0，………12分 n1 n2 n n1 n2 n 下面证明：对于一般的△OMN，其中O(0，0)，M(x ，y )，N(x ，y )， 3 3 4 4 1 1 其面积S  |OM ||ON|sinMON  |OM |2|ON|2 sin2MON 2 2 1  |OM |2|ON |2 |OM |2|ON |2 cos2MON 2 3   2 OMON 1  |OM |2|ON|2 |OM |2|ON|2 2 |OM |2|ON|2 1    2  |OM |2|ON|2  OMON 2 1  (x 2 y 2)(x 2 y 2) x x  y y 2 2 3 3 4 4 3 4 3 4 1  x y  y x 2 3 4 3 4 1 1 故S  x y x y  y y (y  y ) 2bt 2 2t ，n≥2………13分 n 2 n1 n2 n2 n1 8 n1 n2 n1 n2 n n b2 1 |PS| 1 |1k k | 8 8b2 4 b 又   1 2     2 2， |SQ| |tanSPQ| |k k | b 2b b 2 1 2 4 |PS| 当且仅当b2 2时 取最小值………14分 |SQ| 2n 2n 此时t  ，n≥2时有 2t  2， n 2 2 n 2   2 所以S 2 2 2t 2 2t  4t 2t 1 4 2t 2 4t  4n  22n，n≥2………15分 n n n n n n n 2 1 1 2 1 n=1时，T a     ………16分 1 1 S 4 2 8 4 2 1 1 1 1 n≥2时，a     ， n S 2n1  22n  2  2n12n 24n n1  n1 1 1 1    2 1 16   4   2 1  1 n1 2 1 5 1 1 T      1         ， n 8 2 1 8 24  4  8 24 24 24 4 1   4 1 综上，T  . ………17分 n 2p 4