文档内容
专题 02 一元二次函数、方程和不等式
(3 种经典基础练+3 种优选提升练)
等式性质与不等式性质(共10题)
一、单选题
1.(22-23高一上·甘肃酒泉·期末)铁路总公司关于乘车行李规定如下:乘坐动车组列车携带品的
外部尺寸长、宽、高之和不超过130cm,且体积不超过 ,设携带品外部尺寸长、宽、高
分别记为a,b,c(单位:cm),这个规定用数学关系式可表示为( )
A. 且 B. 且
C. 且 D. 且
【答案】C
【分析】根据数量关系列不等式,“不超过”不等号为“小于等于”.
【详解】由长、宽、高之和不超过130cm得 ,由体积不超过 得 .
故选:C.
2.(23-24高一上·云南昆明·期末)已知 ,则下列命题为真命题的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
【答案】C
【分析】根据题意,结合不等式的基本性质,以及特例和作差比较法,逐项判定,即可求解.
【详解】对于A中,例如: ,满足 ,但 ,所以A不正确;
学科网(北京)股份有限公司对于B中,例如: ,满足 ,但 ,所以B不正确;
对于C中,由 ,
因为 ,可得 且 ,所以 ,所以C正确;
对于D中,由 ,可得 ,可得 ,
所以 ,所以D不正确.
故选:C.
3.(23-24高一上·辽宁沈阳·期末)已知 , , ,则( )
A. B. C. D.
【答案】D
【分析】根据不等式的性质即可比较大小.
【详解】因为 ,
故 ,
,
,
即 ,
故 .
故选:D.
4.(22-23高一上·广东湛江·期末)下列命题中正确的是( )
A.若 ,则 B.若 ,则
C.若 ,则 D.若 ,则
学科网(北京)股份有限公司【答案】A
【分析】利用不等式的性质逐个判断各个选项即可.
【详解】对于A,若 ,又 ,则 ,故A正确,
对于B,若 , ,满足 ,但是 ,故B错误,
对于C,若 ,则 ,故C错误,
对于D,若 , ,满足 ,但是 ,故D错误,
故选:A.
二、多选题
5.(23-24高一上·宁夏石嘴山·期末)英国数学家哈利奥特最先使用“>”和“<”符号,并逐渐被数
学界接受,不等号的引入对不等式的发展影响深远,若 ,则( )
A. B. C. D.
【答案】CD
【分析】根据不等式的性质及特殊值法可判断各选项.
【详解】选项A:若 ,则 ,故A错误;
选项B:若 ,则 ,故B错误;
选项C:因为 ,则 ,即 ,故C正确;
选项D:因为 ,则 ,即 ,故D正确;
故选:CD.
6.(21-22高一上·江苏镇江·期末)对于实数 , , ,正确的命题是( )
A.若 ,则 B.若 ,则
C.若 ,则 , D.若 , ,则
【答案】ABD
学科网(北京)股份有限公司【分析】利用作差法,作商法和特值法依次判断选项即可.
【详解】对选项A,因为 ,所以 , ,
所以 ,故A正确;
对选项B, , ,所以 ,
因为 ,所以 ,即 ,故B正确;
对选项C,令 , ,满足 ,不满足 , .
对选项D,因为 , ,
所以 ,故D正确.
故选:ABD
7.(23-24高一上·浙江湖州·期末)若 , , ,则下列命题正确的是( )
A.若 且 ,则 B.若 且 ,则
C.若 ,则 D.
【答案】BD
【分析】利用特殊值判断A,利用作差法判断B、C、D.
【详解】对于A:当 , 时,满足 且 ,但 ,故A错误;
对于B:因为 且 ,
所以 ,故 ,故B正确;
对于C:因为 ,所以 ,即 ,故C错误;
对于D:因为 ,
所以 ,故D正确.
学科网(北京)股份有限公司故选:BD.
8.(23-24高一上·广西贺州·期末)若 , ,则下列不等关系正确的是( )
A. B. C. D.
【答案】ABD
【分析】直接利用不等式的性质判断ABC,作差法判断D.
【详解】对A, , ,由不等式性质易知 ,故A正确;
对B, , ,则 ,故B正确;
对C, , ,由不等式性质易知 ,故C错误;
对D, 若 ,则 , 故D正确.
故选:ABD.
9.(23-24高一上·安徽·期末)已知 ,则下列结论成立的是()
A. B.若 .则
C.若 ,则 D.
【答案】AC
【分析】对于A,用作差法比较大小即可;对于B,举特殊情况即可判断;对于C,用作差法比较即可;
对于D,用作差法比较即可.
【详解】对于 ,因为 ,所以 ,
即 , ,即 故 ,故 正确;
对于 ,若 则 ,故 错误;
对于 ,即 ,故 正确;
对于 , ,故 错误.
故选: .
学科网(北京)股份有限公司三、解答题
10.(23-24高一上·陕西榆林·期中)证明下列不等式:
(1)已知 ,求证: ;
(2)已知 ,求证: .
【答案】(1)证明见解析
(2)证明见解析
【分析】(1)依题意可得 ,再根据不等式的性质证明;
(2)利用作差法证明即可.
【详解】(1) ,即 ,
,则 .
(2) ,
,
,
则 ,
基本不等式(共14题)
一、单选题
1.(23-24高一上·浙江·期末)已知 , ,且 ,则 的最小值为( )
A.4 B.6 C.8 D.9
【答案】D
【分析】根据题意,以 与 为基本量加以整理,化简后利用基本不等式算出答案.
学科网(北京)股份有限公司【详解】由 得 ,其中 , ,
所以 ,
当且仅当 ,即 ,则 , 时,等号成立,
故 的最小值为9.
故选:D
2.(22-23高一上·广东深圳·期末)若x,y满 ,则( )
A. B. C. D.
【答案】C
【分析】由基本不等式的性质进行逐一判断即可.
【详解】因为 ,当且仅当 时取等号,
所以 ,
因为 ,
而 ,所以 ,
于是有 ,故选项AB都不正确;
由 ,
故选:C
3.(23-24高一上·贵州安顺·期末)若不等式 恒成立,则实数 的最大值为
( )
学科网(北京)股份有限公司A.2 B.3 C.4 D.9
【答案】D
【分析】化简可得 恒成立,再根据基本不等式求解 的最小值即可.
【详解】由题意 恒成立,即 恒成立.
又 ,当且仅当 时取等号.
故实数 的最大值为9.
故选:D
4.(23-24高一上·云南昆明·期末)如图,为满足居民健身需求,某小区计划在一块直角三角形空
地中建一个内接矩形健身广场(阴影部分),则健身广场的最大面积为( )
A. B. C. D.
【答案】C
【分析】设出边长,利用相似得到定值,再利用基本不等式求解即可.
【详解】设矩形广场的长为 ,宽为 ,且 , ,
由三角形相似性质得 ,化简得 ,
而 ,当且仅当 时取等,故 ,
故健身广场的最大面积为 .
故选:C
二、多选题
5.(23-24高一上·福建漳州·期末)已知 , ,且 ,则( )
学科网(北京)股份有限公司A. 的最大值为 B. 的最小值为
C. 的最小值为2 D. 的最大值为8
【答案】BC
【分析】A选项,利用基本不等式直接进行求解;B选项,利用基本不等式“1”的妙用求出最值;C
选项, 两边平方后,利用基本不等式求出答案;D选项,变形得到
,D错误.
【详解】A选项,因为 ,由基本不等式得 ,
即 ,故A错误;
B选项,因为 ,
所以 ,
当且仅当 ,即 时,等号成立,
故 的最小值为 ,B正确;
C选项, 两边平方得 ,
,其中 ,
当且仅当 ,即 时,等号成立,
故 ,解得 ,
的最小值为2,C正确;
D选项,因为 , ,
所以 ,
学科网(北京)股份有限公司故D错误.
故选:BC
6.(23-24高一上·山东枣庄·期末)已知a,b,c满足 ,且 ,则( )
A. B. C. D.
【答案】ABD
【分析】首先利用放缩法证明出 , ,从而可以判断ABC,对于D则需要使用基本不等式.
【详解】因为 ,所以 ,即 , ,即 ,
所以 ,故AB正确C错误;
对于D: ,故D正确.
故选:ABD
7.(22-23高一上·广东茂名·期末)已知 ,且 ,则( )
A. B.
C. D.
【答案】ABD
【分析】利用基本不等式的性质依次判断选项即可得到答案.
【详解】对选项A,因为 ,所以 ,
当且仅当 时等号成立,故A正确.
对选项B,因为 , ,且 ,
所以 .
当且仅当 ,即 时等号成立,故B正确.
对选项C, ,
当且仅当 时等号成立,故C错误.
学科网(北京)股份有限公司对选项D, ,且 ,所以 ,
即 ,当且 时等号成立.
所以 ,
所以 ,故D正确.
故选:ABD
8.(23-24高一上·河南安阳·期末)下列说法正确的是( )
A. ,则 的最小值是2
B. ,则 的最小值是
C. ,则 的最小值是1
D. 的最小值为9
【答案】BD
【分析】根据选项式子的特点,利用函数单调性或者基本不等式可得答案.
【详解】对于A,当 时, ,A不正确;
对于B, ,令 ,则 ,
由对勾函数的单调性可知,当 时, 为增函数,所以 的最小值是 ,B正确;
对于C,令 ,由 得 , ,
由对勾函数的单调性可知,当 时, 为增函数,所以 的最小值是 ,C不正确;
对于D,由 可得 , ,
学科网(北京)股份有限公司当且仅当 ,即 时,取到等号,D正确.
故选:BD.
三、填空题
9.(22-23高一上·广东广州·期末)已知 , ,且 ,若 恒成立,则实数
的取值范围是 .
【答案】
【分析】将 与 相乘,展开后利用基本不等式求出 的最小值,即可得出实数 的
取值范围.
【详解】因为 , ,且 ,
所以, ,
当且仅当 时,等号成立,故 的最小值为 .
因为 恒成立,所以, .
故答案为: .
10.(23-24高一上·河南·期末)已知 ,且 ,则 的最大值是 .
【答案】
【分析】直接利用基本不等式计算即可.
【详解】因为 ,所以
学科网(北京)股份有限公司因为 ,所以 ,即 .
当且仅当 ,即 时,等号成立.
所以 的最大值是 .
故答案为: .
11.(21-22高一上·江西南昌·期末)当 时,函数 的最小值为 .
【答案】
【分析】将函数解析式变形为 ,利用基本不等式可求得结果.
【详解】因为 ,则 ,则
,
当且仅当 时,等号成立,
所以,当 时,函数 的最小值为 .
故答案为: .
四、解答题
12.(23-24高一上·四川遂宁·期末)(1)已知 ,求 的最大值;
(2)已知 ,求 的最小值.
学科网(北京)股份有限公司【答案】(1) ;(2)
【分析】(1)利用基本不等式即可得解;
(2)利用基本不等式,结合换元法即可得解.
【详解】(1)因为 ,所以 ,
则 ,当且仅当 ,即 时,取到等号,
所以 的最大值为 ;
(2)因为 ,所以 ,
令 ,则 ,
所以 ,
当且仅当 ,即 ,即 时,取到等号,
所以 的最小值为 .
13.(22-23高一上·陕西榆林·期末)已知 , .
(1)若 ,求 的最大值;
(2)若 ,证明: .
【答案】(1)9
(2)证明见解析
【分析】(1)由 运用基本不等式求乘积得最大值;
(2)直接由基本不等式 对已知等式进行放缩,证得结果.
【详解】(1)因为 ,所以 .
学科网(北京)股份有限公司,
当且仅当 , , 时,等号成立,
故 的最大值为9.
(2)证明:因为 ,
所以 ,又 ,
解得 ,
当且仅当 时,等号成立.
故 .
14.(22-23高一上·河南·期末)证明下列不等式,并讨论等号成立的条件.
(1)若 ,则 ;
(2)若 ,则 .
【答案】(1)答案见解析
(2)答案见解析
【分析】(1)利用基本不等式即可证明;
(2)讨论 和 两种情况,脱掉绝对值符号,结合基本不等式证明即可.
【详解】(1)证明:因为 ,所以 , ,
所以 ,
当且仅当 ,即 时,等号成立.
学科网(北京)股份有限公司(2)证明:因为 ,当 时, ,
当且仅当 时等号成立.
当 时, ,
当且仅当 时等号成立.
综上,若 ,则 成立,当且仅当 时等号成立.
二次函数与一元二次方程、不等式(共20题)
一、单选题
1.(23-24高一上·江苏徐州·期末)若命题“ , ”是假命题,则实数 的最小值
为( )
A.1 B.2 C.4 D.8
【答案】C
【分析】根据特称命题与全称命题的真假性质,结合一元二次不等式的解集的性质进行求解即可.
【详解】因为命题“ , ”是假命题,
所以命题“ , ”是真命题,
因此有 ,所以实数 的最小值为 ,
故选:C
2.(23-24高一上·安徽宣城·期末)若命题“ ,使 ”是真命题,则实数m的取
值范围是( )
A. B. C. D.
【答案】C
学科网(北京)股份有限公司【分析】由存在性问题得 即可得解.
【详解】由题意命题“ ,使 ”是真命题,所以 ,
当且仅当 ,有 ,所以实数m的取值范围是 .
故选:C.
3.(22-23高一上·河北保定·期末)关于二次函数 ,则下列正确的是( )
A.函数图象与x轴总有两个不同的交点
B.若函数图象与x轴正半轴交于不同的两点,则
C.不论k为何值,若将函数图象向左平移1个单位,则图象经过原点
D.当 时,y随x的增大而增大,则
【答案】C
【分析】根据二次函数对应二次方程的判别式判断A,由根与系数的关系判断B,由图象的平移判
断C,根据对称轴判断D.
【详解】 , 函数图象与x轴总有两个不同的交点或
相同的交点,故A错误;
若函数图象与x轴正半轴交于不同的两点,则由根与系数的关系知 ,解得 且 ,
故B错误;
若将函数图象向左平移1个单位,可得到 ,令 ,则 ,即图象经
过原点,故C错误;
当 时,y随x的增大而增大,即函数图象的对称轴 ,解得 ,故D错误.
故选:C
4.(23-24高一上·江苏南京·期末)若函数 在区间 上单调递减,则实数
的取值范围是( )
A. B. C. D.
学科网(北京)股份有限公司【答案】D
【分析】利用二次函数的对称轴及函数的单调性列出不等式求解.
【详解】因为函数 在区间 上单调递减,
所以 ,解得 .
故选:D
二、多选题
5.(23-24高一上·内蒙古巴彦淖尔·期末)已知命题 : ,则命题 成立的一个充分
不必要条件是( )
A. B. C. D.
【答案】AB
【分析】解不等式求得 : ,利用充分不必要条件的概念计算即可.
【详解】由 ,解得 .
要满足题意,只需在 的子集中确定即可,
显然 和 都是命题 成立的充分不必要条件.
故选:AB.
6.(23-24高一上·湖北十堰·期末)已知关于 的不等式. 的解集为 .
则( )
A.
B.不等式 的解集是
C.
D.不等式 的解集为 或
【答案】AC
【分析】由条件可得 为方程 的两根,且 ,结合根与系数关系可得 的关
系,再逐项判断各选项.
学科网(北京)股份有限公司【详解】因为不等式. 的解集为 ,
所以 为方程 的两根,且 ,
所以 , ,
所以 , , ,
因为 ,所以A正确;
因为 , , ,
所以不等式 可化为 ,B错误;
因为 , , ,
所以 ,C正确;
因为 , , ,
所以不等式 可化为 ,
解得, ,所以D错误;
故选:AC.
7.(23-24高一上·安徽宣城·期末)对任意的 ,函数 的值域是 .
则下列结论中正确的是( )
A. B.
C. 的最小值是12 D. 的最小值是
【答案】ABC
【分析】由题意可得 ,且 ,从而可求得 的关系,即可判断AB;再根据基本不
等式判断CD即可.
【详解】因为函数 的值域是 ,
所以 ,且 ,
学科网(北京)股份有限公司即 ,所以 ,故AB正确;
由 ,得 ,
则 ,
当且仅当 ,即 时,取等号,
所以 的最小值是12,故C正确;
由 ,得 ,
则 ,
当且仅当 ,即 时取等号,
所以 的最小值是 ,故D错误.
故选:ABC.
8.(23-24高一上·江西抚州·期末)若正实数 满足 ,则下列结论中正确的有( )
A. 的最小值为8.
B. 的最小值为
C. 的最大值为 .
D. 的最小值为 .
【答案】ABC
【分析】利用基本不等式求解最值判断A,B,C,利用消元法结合二次函数求得最值判断D.
【详解】A选项,因为 ,且 ,所以 ,
学科网(北京)股份有限公司所以 ,当且仅当 时,等号成立,
,当且仅当 时,等号成立,故A正确;
B选项,因为
,
当且仅当 ,即 时取等号,故B项正确;
C选项, ,
当且仅当 时取等号,所以 ,所以 的最大值为 ,故C项正
确;
D选项,因为 ,当且仅当 时取等
号,
所以 的最小值为 ,故D项错误.
故选:ABC.
【点睛】思路点睛:四个选项均要对所求式子进行变形,A,B,C选项利用“1”代换以及基本不
等式求最值,同时也要注意取等条件是否成立,D选项由条件消元转换成二次函数求最值.
三、填空题
9.(23-24高一上·安徽亳州·期末)若关于 的不等式 的解集为 ,则实数 的取值
范围为 .
【答案】
【分析】由一元二次不等式的解集为 ,可知二次函数开口向上,判别式小于0,解得即可.
【详解】当 时, , ,不满足题意;
学科网(北京)股份有限公司当 时, ,所以 ,
综上,实数 的取值范围为 .
故答案为:
10.(23-24高一上·江西九江·期末)设二次函数 的值域是 ,则
的最小值是 .
【答案】2
【分析】由二次函数值域确定参数关系,结合基本不等式即可求解.
【详解】根据题意知, , ,即 ,
所以 ,当且仅当 即 时等号成立.
所以 的最小值是2.
故答案为:2.
11.(23-24高一上·新疆阿克苏·期末)已知不等式 对于任意实数x恒成立,实数
a的取值范围 .
【答案】
【分析】由不等式 对于任意实数 恒成立,可得 ,从而得解.
【详解】由不等式 对于任意实数 恒成立,可得 ,
即 ,解得 .
故答案为: .
12.(22-23高一上·江苏淮安·期末)设 表示函数 在闭区间 上的最大值.若正
实数 满足 ,则正实数 的取值范围是 .
学科网(北京)股份有限公司【答案】
【分析】根据 的表达式,画出其图象,根据图象,分 和 两种情况讨论,结合图象得
在区间 的最大值即可列不等式求解.
【详解】函数 的图像如下:
的对称轴为 , ;当 时, ,
分类讨论如下:
(1)当 时, , ,
依题意, ,而函数在 时是增函数,此时 , ,故不可能;
(2)当 时, ,
依题意, ,即 ,
令 ,解得: ,
则有: 并且 ,解得: ;
或者 并且 ,无解;
综上:
故答案为:
学科网(北京)股份有限公司13.(23-24高一上·江苏盐城·期末)关于 的不等式 在 上有解,则实数 的取
值范围是 .
【答案】
【分析】根据题意将不等式转化为 在 能成立即可,再由二次函数性质求出
即可得 的取值范围是 .
【详解】由不等式 以及 可得 ,
依题意可知 即可,
令 ,
又 ,由 可得 ,
利用二次函数性质可知 ,即可得 ;
即实数 的取值范围是 .
故答案为:
14.(23-24高一上·重庆·期末)关于x的一元二次方程 有一个根小于 ,
另一个根大于1,则a的取值范围是 .
【答案】
【分析】根据二次函数图像特征,满足 ,即得a的取值范围.
【详解】设 ,开口向上,
学科网(北京)股份有限公司由题意知 ,
即 ,解得 ,
所以 .
故答案为: .
四、解答题
15.(23-24高一上·新疆阿克苏·期末)(1)求不等式 的解集;
(2)求函数 的最小值.
【答案】(1) .
(2)5.
【分析】(1)把不等式因式分解,因为开口向上,所以小于0取中间,得到结果;
(2)利用均值不等式相关知识进行求解.
【详解】(1) ,
,所以不等式的解集为 .
(2)
当且仅当 即 时,取等号.
16.(23-24高一上·河北唐山·期末)已知函数 .
(1)若 ,求不等式 的解集;
学科网(北京)股份有限公司(2)若函数 的图象与 轴交于 , 两点,求 的最小值.
【答案】(1) 或
(2)
【分析】(1)解一元二次不等式,求出解集;
(2) ,由韦达定理得到两根之和,两根之积,进而得到
,求出最小值.
【详解】(1) 时, ,解得 或 ,
原不等式的解集为 或 ;
(2)令 ,
由 得 ,
故 ,
故
,
当 时, 取得最小值,最小值为 .
17.(23-24高一上·黑龙江牡丹江·期末)设命题 :实数 满足 ,其中 ,命
题 :实数 满足 .
学科网(北京)股份有限公司(1)若 ,且 和 都是真命题,求实数 的取值范围;
(2)若 是 的充分不必要条件,求实数 的取值范围.
【答案】(1) ;
(2) .
【分析】(1)把 代入,求出命题 为真命题的 范围,再求出公共部分即得.
(2)求出命题 为真命题的 范围,再充分不必要条件的意义列式求解即得.
【详解】(1)当 时,不等式 为 ,解得 ,即
,
由 ,得 ,即 ,
由 和 都是真命题,得 ,
所以实数 的取值范围是 .
(2)由 , ,得 ,即命题 ,由(1)知命题 ,
因为 是 的充分不必要条件,因此 或 ,解得 或 ,即 ,
所以实数 的取值范围是 .
18.(22-23高一上·湖南邵阳·期末)已知二次函数 的图象过点 .
(1)求 的解析式,并写出 的单调递增区间(不要求证明);
(2)求不等式 的解集.
【答案】(1) , ;
(2) .
【分析】(1)由题意可得 ,求解即可;
(2)原不等式可转化为 ,根据一元二次不等式的解法求解即可.
【详解】(1)因为函数 的图象过点 ,
学科网(北京)股份有限公司所以 ,解得 .
所以 的解析式为 .
,故 的单调递增区间为 .
(2) 即为 ,
即 ,解得 或 .
故不等式 的解集为 .
19.(22-23高一上·湖北黄冈·期末)设函数 .
(1)若不等式 的解集为 ,求 的值;
(2)若 ,且 都有 ,求 的最大值.
【答案】(1)
(2)
【分析】(1)根据一元二次不等式的解集即可求解;
(2)根据题意可得函数关于直线 对称,利用二次函数的对称轴得出 ,再结合基本不等
式即可求解.
【详解】(1)依题意可知: 和 是方程 的两根,
则有 且
∴
(2)由 知 关于直线 对称,
即
学科网(北京)股份有限公司当且仅当 时等号成立.
∴ 的最大值为
20.(23-24高一上·江苏无锡·期末)已知函数 ,
.
(1)若 在区间 上最大值为2,求实数 的值;
(2)当 时,求不等式 的解集.
【答案】(1) ;
(2)答案见解析.
【分析】(1)求出二次函数图象的对称轴,再利用二次函数性质求解即得.
(2)分类讨论求解含参数的一元二次不等式即得.
【详解】(1)函数 图象的对称轴为 ,
当 ,即 时, ,解得 ,则 ;
当 ,即 时, ,解得 ,矛盾,
所以 .
(2)显然 ,而 ,
因此不等式为 ,
当 ,即 时,不等式解集为 ;
当 ,即 时,不等式解集为 ;
当 ,即 时,不等式解集为 ,
学科网(北京)股份有限公司所以当 时,不等式解集为 ;当 时,不等式解集为 ;当 时,不等式解集为
.
最值问题(共9题)
一、填空题
1.(22-23高一上·重庆九龙坡·期中)已知 , , 是正实数,且 ,则 最
小值为 .
【答案】
【分析】首先变形为 ,再根据 ,变形为
,展开后,利用基本不等式求最小值,最后再用基本不等式求
最小值.
【详解】由题, ,
其中
,
学科网(北京)股份有限公司当且仅当 ,即 时取等,
故
,
当且仅当 时,即 时取等.
故答案为:
2 . ( 23-24 高 一 上 · 山 东 菏 泽 · 期 末 ) 若 、 、 、 均 为 正 实 数 , 则
的最小值为 .
【答案】
【分析】
从最后两项开始,逐次使用基本不等式,可求得所求代数式的最小值.
【详解】原式
,
学科网(北京)股份有限公司当且仅当 时,
即当 时,等号成立,
故 的最小值为 ,
故答案为: .
【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:
(1)“一正二定三相等”“一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则
必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定
值就不是所求的最值,这也是最容易发生错误的地方.
3.(23-24高一上·安徽蚌埠·期末)已知实数 且 ,则 的
最大值为 ,最小值为 .
【答案】
【分析】由已知 , ,
由基本不等式和配方法求最大值, ,由配方法求最小值.
【详解】已知实数 且 ,
则 ,
,
当 或 时等号成立,即 的最大值为1;
学科网(北京)股份有限公司,当 , 或 时等号成立,
即 的最小值为 .
故答案为: ; .
【点睛】方法点睛:已知条件下求 的最值,要利用好 ,即 可化为
,由 可利用基本不等式求积的最小值,二次三项式可以用配方法求最值.
二、解答题
4.(23-24高一上·山西长治·期末)已知 , .
(1)当 时,求 的最小值;
(2)当 时,求 的最小值.
【答案】(1)9
(2)5
【分析】(1)利用基本不等式结合二次不等式求解即可;
(2)利用基本不等式中常数代换技巧求解最值即可.
【详解】(1)当 时, ,即 ,
所以 ,即 ,当且仅当 时等号成立,所以 的最小值为9;
(2)当 时, ,即 ,
所以 ,
学科网(北京)股份有限公司当且仅当 ,即 时等号成立,所以 的最小值为5.
5.(23-24高一上·甘肃·期末)已知 .
(1)求证: ;
(2)若 ,求 的最小值.
【答案】(1)证明见解析;
(2)8.
【分析】(1)根据给定条件,利用基本不等式推理即得.
(2)利用基本不等式“1”的妙用求出最小值.
【详解】(1) ,则 ,当且仅当 时取等
号,
所以 .
(2)由 ,且 ,得 ,
当且仅当 ,即 时取等号,
所以当 时, 取得最小值8.
6.(23-24高一上·贵州贵阳·期末)《见微知著》谈到:从一个简单的经典问题出发,从特殊到一
般,由简单到复杂:从部分到整体,由低维到高维,知识与方法上的类比是探索发展的重要途径,
是思想阀门发现新问题、新结论的重要方法.
阅读材料一:利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找
到简便解决方法,常用的途径有:(1)整体观察:(2)整体设元;(3)整体代入:(4)整体
求和等.
例如, ,求证: .
证明:原式 .
学科网(北京)股份有限公司阅读材料二:解决多元变量问题时,其中一种思路是运用消元思想将多元问题转化为一元问题,再
结合一元问题处理方法进行研究.
例如,正实数 满足 ,求 的最小值.
解:由 ,得 ,
,
当且仅当 ,即 时,等号成立.
的最小值为 .
波利亚在《怎样解题》中指出:“当你找到第一个蘑菇或作出第一个发现后,再四处看看,他们总
是成群生长”类似问题,我们有更多的式子满足以上特征.
结合阅读材料解答下列问题:
(1)已知 ,求 的值;
(2)若正实数 满足 ,求 的最小值.
【答案】(1)1
(2) .
【分析】(1)将1化成 ,约分即可求解,
(2)利用将1化成 ,即可得 ,通分后分离常数,即可利用基本不等式求解,
或者利用 ,代入后得 ,即可求解.
【详解】(1)由题意得
;
(2)解法1(整体代入):由
学科网(北京)股份有限公司,
由于 ,故 ,当且仅当 ,即 时等号成立,
因为 有最小值 ,此时 有最大值 ,
从而 最小值 ,即 有最小值 .
解法2(消元思想):由题意得 .
因为 ,当且仅当 ,即 时等号成立,
因为 有最小值 ,此时 有最大值 ,
从而 最小值 ,即 有最小值 .
7.(23-24高一上·辽宁朝阳·期末)冷链物流是指以冷冻工艺为基础、制冷技术为手段,使冷链物
品从生产、流通、销售到消费者的各个环节始终处于规定的温度环境下,以减少冷链物品损耗的物
流活动.随着人民食品安全意识的提高及线上消费需求的增加,冷链物流市场规模也在稳步扩大.某
学科网(北京)股份有限公司冷链物流企业准备扩大规模,决定在2024年初及2025年初两次共投资4百万元,经预测,每年初
投资的 百万元在第 ( ,且 )年产生的利润(单位:百万元)
,记这4百万元投资从2024年开始的第 年产生的利润之和
为 .
(1)比较 与 的大小;
(2)求两次投资在2027年产生的利润之和的最大值.
【答案】(1)
(2)
【分析】(1)由 求出 , ,再由作差法比较大小即可得出答案.
(2)先求出两次投资在2027年产生的利润之和 ,再由基本不等式或判别式
求出 的最大值.
【详解】(1) 表示2024年及2025年各投资2百万元,
由题意得 ,
,
,
所以 .
(2)两次投资在2027年产生的利润之和为 百万元,
学科网(北京)股份有限公司设2024年初投资 百万元,则2025年初投资 百万元,
2024年初投资的 百万元在2027年产生的利润为 (百万元),
2025年初投资的 百万元在2027年产生的利润为 (百万元),
所以 .
解法一:
,设 ,
则 ,两边平方得 ,
由 得 ,所以 ,
当 时取等号.
所以 , .
所以两次投资在2027年产生的利润之和的最大值为 百万元.
解法二:
,
当且仅当 ,即 时取等号,
所以 ,两次投资在2027年产生的利润之和的最大值为 百万元.
8.(23-24高一上·广东广州·期末)某食品企业为了提高其生产的一款食品的收益,拟在下一年度
开展促销活动,已知该款食品年销量 吨与年促销费用 万元之间满足函数关系式 (
为常数),如果不开展促销活动,年销量是1吨.已知每一年生产设备折旧、维修等固定费用为3
万元,每生产1吨食品需再投入32万元的生产费用,通过市场分析,若将每吨食品售价定为:
“每吨食品平均生产成本的1.5倍”与“每吨食品平均促销费的一半”之和,则当年生产的该款食
学科网(北京)股份有限公司品正好能销售完.
(1)求 值;
(2)将下一年的利润 (万元)表示为促销费 (万元)的函数;
(3)该食品企业下一年的促销费投入多少万元时,该款食品的利润最大?
(注:利润 销售收入 生产成本 促销费,生产成本 固定费用 生产费用)
【答案】(1)
(2)
(3)该食品企业下一年的促销费投入6万元时,该款食品的利润最大为 万元.
【分析】(1)依题意当 时, 代入计算可得;
(2)依题意求出当年生产 吨时,求出年生产成本和为年销售收入,从而可表示出食品的利润;
(3)由(2)可得 ,利用基本不等式计算可得.
【详解】(1)由题意可知,当 时, ,所以 ,解得 ;
(2)由于 ,故 ,
由题意知,当年生产 吨时,年生产成本为: ,
当销售 吨时,年销售收入为: ,
由题意, ,
即 .
(3)由(2)知: ,
即
,
学科网(北京)股份有限公司当且仅当 ,又 ,即 时,等号成立.
此时, .
该食品企业下一年的促销费投入6万元时,该款食品的利润最大为 万元.
9.(23-24高一上·河北石家庄·期末)对于定义域为 的函数 ,如果存在区间 ,
同时满足:① 在 内是单调函数;②当定义域是 时, 的值域也是 ,则称
是该函数的“优美区间”.
(1)求证: 是函数 的一个“优美区间”;
(2)已知函数 ( , )有“优美区间” ,当 变化时,求出
的最大值.
【答案】(1)证明见解析
(2)
【分析】(1)通过 在区间 上单调递增,利用新定于判断即可证明;
(2)设 是已知函数定义域的子集,通过 是已知函数的“优美区间”,则 ,
说明 , 是方程 的两个同号且不等的实数根,转化求解 的最大值.
【详解】(1)因为 在区间 上单调递增,
又 , ,
所以 的值域为 ,
学科网(北京)股份有限公司所以区间 是 的一个“优美区间”.
(2)设 是已知函数定义域的子集,
因为 的定义域为 ,则 或 ,
而函数 在 上单调递增,
若 是已知函数的“优美区间”,则 ,
所以 , 是方程 ,即 的两个同号且不等的实数根,
因为 ,
所以 , 同号,只需 ,
解得 或 ,
因为 ,
所以当 时, 取得最大值 .
【点睛】关键点睛:本题第二问的关键是将 转化为方程 的两个同号且不
等的实数根,再结合 ,代入计算即可.
基本不等式的应用(共11题)
1.(23-24高一上·河南开封·期末)如图,一份印刷品的排版(阴影部分)为矩形,面积为 32,
它的左、右两边都留有宽为2的空白,上、下两边都留有宽为 1的空白.记纸张的面积为 S,排版
矩形的长和宽分别为x,y.
学科网(北京)股份有限公司(1)用x,y 表示 S;
(2)如何选择纸张的尺寸,才能使纸张的面积最小? 并求最小面积.
【答案】(1)
(2)纸张的长和宽分别为12,6时,纸张的面积最小,最小面积为72.
【分析】(1)由题意知 ,再代入 化简即可;
(2)利用基本不等式即可求出最值.
【详解】(1)由题意, ,
.
(2) ,
当且仅当 ,即 时等号成立,
所以纸张的长和宽分别为12,6时,纸张的面积最小,最小面积为72.
2.(22-23高一上·江苏宿迁·期末)汽车在隧道内行驶时,安全车距 (单位: )正比于车速
(单位: )的平方与车身长 (单位: )的积,且安全车距不得小于半个车身长.当车速
为 时,安全车距为 个车身长.
(1)求汽车在隧道内行驶时的安全车距 与车速 之间的函数关系式;
(2)某救灾车队共有10辆同一型号的货车,车身长为 ,当速度为多少时该车队通过(第一辆车
头进隧道起,到最后一辆车尾离开隧道止,且无其它车插队)长度为 的隧道用时最短?
【答案】(1)
(2) km/h
【分析】(1)根据题意 为定值,设比例常数为 ,则 ,代入数值,得到 ,令
,则 ,最后写出分段函数解析式即可;
学科网(北京)股份有限公司(2)设通过隧道的时间为 ,则 ,分当 和 两种情况,结合幂函数的
性质及基本不等式计算可得.
【详解】(1)根据题意 为定值,设比例常数为 ,则 ,
所以 ,所以 ,
所以 ,令 ,则 ,
所以 .
(2)设通过隧道的时间为 ,则 .
①当 时, .
②当 时,
.
当且仅当 ,即 时等号成立.
又 ,
所以当 时用时最短.
答:当速度为 时该车队通过该隧道用时最短.
3.(22-23高一上·湖北武汉·期末)某企业研发部原有 名技术人员,年人均投入 万元,现将
这 名技术人员分成两部分:技术人员和研发人员,其中技术人员 名,调整后研发人
员的年人均投入增加 ,技术人员的年人均投入调整为 万元
(1)要使这 名研发人员的年总投入不低于调整前的 名技术人员的年总投入,求调整后的技
术人员的人数 最多为多少人?
(2)若技术人员在已知范围内调整后,必须研发人员的年总投入始终不低于技术人员的年总投入,
求出正整数 的最大值.
【答案】(1) 人
学科网(北京)股份有限公司(2)
【分析】(1)根据题意可得出关于 的不等式,结合 ,可解得 的范围,即可得出结论;
(2)根据题意可得出 ,参变量分离可得 ,
结合基本不等式可求得实数 的取值范围.
【详解】(1)解:依题意得 ,整理可得 ,
又因为 ,解得 ,
所以调整后的技术人员的人数最多 人.
(2)解:由研发人员的年总投入始终不低于技术人员的年总投入有:
,得 ,
整理得 ,
由基本不等式可得 ,
当且仅当 时,即当 时等号成立,所以 .
因此,正整数 的最大值为 .
4.(22-23高一上·湖南衡阳·期末)如图为传统节日玩具之一走马灯,常见于除夕、元宵、中秋等
节日灯内点上蜡烛,蜡烛燃烧产生的热力造成气流,令轮轴转动.轮轴上有剪纸,烛光将剪纸的影
投射在屏上,图像便不断走动,因剪纸图像为古代武将骑马的图画,在转动时看起来好像几个人你
追我赶一样,故名走马灯,现打算做一个体积为96000 的如图长方体状的走马灯(题中不考虑
木料的厚薄粗细).
学科网(北京)股份有限公司(1)若底面大矩形的周长为160cm,当底面边长为多少时,底面面积最大?(设大矩形的长为 ,宽
为 )
(2)若灯笼高为40cm,现只考虑灯笼的主要框架,当底面边长为多少时,框架用料最少?
【答案】(1)长宽均为 ;
(2)长为 ,宽为
【分析】(1)由 ,然后利用基本不等式求出 的最大值,从而求解;
(2)由体积一定得 然后利用基本不等式求出 的最小值,从而求解.
【详解】(1)由题意得底面大矩形周长为 ,且大矩形的长设为 ,宽设为 ,
所以 ,得 ,所以 ,
当且仅当 时取等号,此时 ,
所以底面面积最大为 .
(2)由题意知走马灯的体积为 ,高为 ,所以底面积为 ,
框架用料最少等价于底面用料为 最小即可,
学科网(北京)股份有限公司,当 ,即 取等号,
故当长为 、宽为 时,用料最少.
5.(23-24高一上·甘肃临夏·期末)某单位建造一间地面面积为12平方米的背面靠墙的矩形小房,
由于地理位置的限制,房子侧面的长度x不得超过5米,房屋正面的造价为400元/平方米,房屋
侧面的造价为150元/平方米,屋顶和地面的造价费用合计为5800元,如果墙高为3米,且不计房
屋背面的费用,当侧面的长度为多少时,总造价最低?最低总造价是多少元?
【答案】当侧面的长度为4米时,总造价最低.最低总造价是13000元
【分析】根据题意得到函数表达式 ,利用基本不等式求出最小值即可.
【详解】由题可知
因为 ,当且仅当 ,即 时取等号,
所以 在 时取最小值 ,
于是当侧面的长度为 米时,总造价最低.最低总造价是 元.
6.(23-24高一上·广东深圳·期末)某公司为了提高生产效率,决定投入160万元买一套生产设备,
预计使用该设备后,前 年的支出成本为 万元,每年的销售收入98万元.使用若
干年后对该设备处理的方案有两种,方案一:当总盈利额达到最大值时,该设备以20万元的价格
处理;方案二:当年平均盈利额达到最大值时,该设备以30万元的价格处理.哪种方案较为合理?
并说明理由.(注:年平均盈利额 )
【答案】方案二更合理,理由见解析
【分析】分别求出两种方案的总利润,以及所需要的时间,即可得出结论.
【详解】方案二更合理,理由如下:
设 为前 年的总盈利额,单位:万元;
由题意可得 ,
学科网(北京)股份有限公司方案一:总盈利额 ,
当 时, 取得最大值 ;此时处理掉设备,则总利润为 万元;
方案二:平均盈利额为 ,
当且仅当 ,即 时,等号成立;即 时,平均盈利额最大,此时 ,
此时处理掉设备,总利润为 万元;
综上,两种方案获利都是 万元,但方案二仅需要4年即可,故方案二更合适.
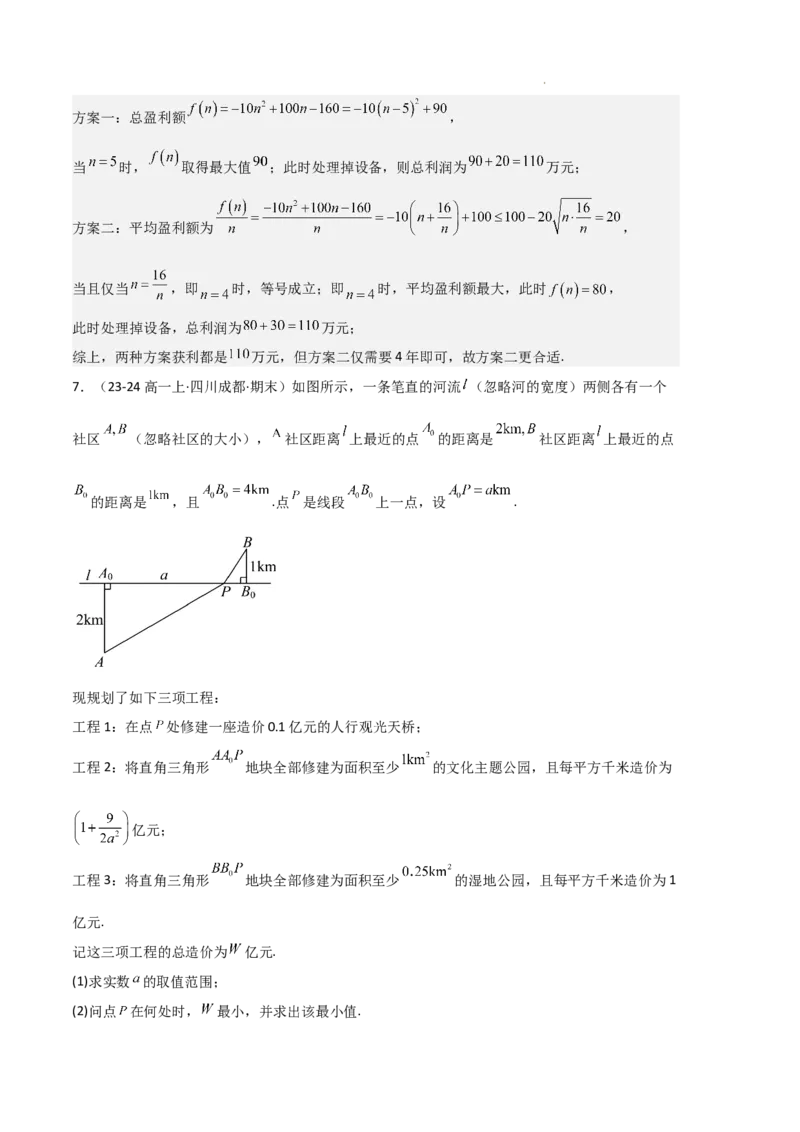
7.(23-24高一上·四川成都·期末)如图所示,一条笔直的河流 (忽略河的宽度)两侧各有一个
社区 (忽略社区的大小), 社区距离 上最近的点 的距离是 社区距离 上最近的点
的距离是 ,且 .点 是线段 上一点,设 .
现规划了如下三项工程:
工程1:在点 处修建一座造价0.1亿元的人行观光天桥;
工程2:将直角三角形 地块全部修建为面积至少 的文化主题公园,且每平方千米造价为
亿元;
工程3:将直角三角形 地块全部修建为面积至少 的湿地公园,且每平方千米造价为1
亿元.
记这三项工程的总造价为 亿元.
(1)求实数 的取值范围;
(2)问点 在何处时, 最小,并求出该最小值.
学科网(北京)股份有限公司【答案】(1)
(2)当点 满足 时, 最小,最小值为 亿元.
【分析】(1)由直角三角形 地块全部修建为面积至少 和直角三角形 地块全部
修建为面积至少 的文化主题公园湿地公园,列不等式求解即可得出答案.
(2)由题意可得 ,由基本不等式求解即可.
【详解】(1)因为直角三角形 地块全部修建为面积至少 的湿地公园,
所以 ,解得:
直角三角形 地块全部修建为面积至少 的文化主题公园,
所以 ,解得: ,
故实数 的取值范围为 .
(2)依题意可得:
,
当且仅当 ,即 时取等.
所以当点 满足 时, 最小,最小值为 亿元.
8.(22-23高一上·山东菏泽·期末)为提高隧道车辆通行能力,研究了隧道内的车流速度 (单位:
学科网(北京)股份有限公司千米/小时)和车流密度 (单位:辆/千米)所满足的关系式: .
研究表明:当隧道内的车流密度达到120辆/千米时造成堵塞,此时车流速度为0千米/小时.
(1)若车流速度 千米/小时,求车流密度 的取值范围;
(2)隧道内的车流量 (单位时间内通过隧道的车辆数,单位:辆/小时)满足 ,求隧道内车
流量 的最大值,并指出车流量最大时的车流密度 辆/千米.
【答案】(1)
(2)最大值为2600辆/小时,此时车流密度 为80辆/千米
【分析】(1)先求解 的值,再利用解析式求解范围;
(2)先表示出 的解析式,利用基本不等式进行求解最值.
【详解】(1)由题意知,当 (辆/千米)时, (千米/小时),代入 得
,
所以
当 时, ,易知符合题意;
当 时, ,解得 ,所以 .
综上,车流密度 的取值范围是 .
(2)由(1)知
所以当 时, 为增函数,所以 ,当且仅当 等号成立;
当 时,
学科网(北京)股份有限公司,
即 ,当且仅当 ,即 等号成立.
综上: 的最大值为2600(辆/小时),此时 (辆/千米).
即隧道内车流量 的最大值为2600辆/小时,此时车流密度 为80辆/千米.
9.(22-23高一上·陕西渭南·期末)某学校要建造一个长方体形的体育馆,其地面面积为 ,
体育馆高 ,如果甲工程队报价为:馆顶每平方米的造价为100元,体育馆前后两侧墙壁平均造
价为每平方米150元,左右两侧墙壁平均造价为每平方米250元,设体育馆前墙长为 米.
(1)当前墙的长度为多少时,甲工程队报价最低?
(2)现有乙工程队也参与该校的体育馆建造竞标,其给出的整体报价为 元
,若无论前墙的长度为多少米,乙工程队都能竞标成功,试求 的取值范围.
【答案】(1)当前墙的长度为20米时,甲工程队报价最低为84000元
(2)当 时,无论前墙的长度为多少米,乙工程队都能竞标成功
【分析】(1)根据题意求出报价的表达式,再根据基本不等式即可得解;
(2)根据题意可知 对任意的 恒成立,分离
参数可得 对任意的 恒成立,分类常数结合基本不等式求出 的最小值,即
可得解.
【详解】(1)因为体育馆前墙长为 米,地面面积为 ,
所以体育馆的左右两侧墙的长度均为 米 ,
设甲工程队报价为 元,
所以 ,
因为 ,
学科网(北京)股份有限公司当且仅当 ,即 时等号成立,
所以当前墙的长度为20米时,甲工程队报价最低为84000元;
(2)根据题意可知 对任意的 恒成立,
即 对任意的 恒成立,
所以 对任意的 恒成立,
因为 ,
,
当且仅当 ,即 时等号成立,
所以 ,
故当 时,无论前墙的长度为多少米,乙工程队都能竞标成功.
10.(22-23高一上·江苏无锡·期末)现有一个无盖长方体形箱体,如图所示,该长方体的长为2米,
宽为x米,高为y米.
(1)如果箱体容积为100立方米,那么至少需要多少平方米制箱材料;
(2)如果制箱材料为60平方米,那么怎样设计箱体能使箱体的容积最大?最大容积是多少?
【答案】(1)至少需要 平方米制箱材料
(2)当 米时,箱体的容积最大,最大容积是 立方米
【分析】(1)先求得几何体的表面积的表达式,然后利用基本不等式求得正确答案.
(2)先求得几何体的体积的表达式,然后利用基本不等式求得正确答案.
【详解】(1)依题意, ,
学科网(北京)股份有限公司需要材料 平方米,
当且仅当 且 ,即 时,等号成立,
所以至少需要 平方米制箱材料.
(2)依题意, ,
则 ,即 ,
所以 ,故 ,
所以箱体的容积 ,
当且仅当 且 ,即 时,等号成立,
所以当 米时,箱体的容积最大,最大容积是 立方米.
11.(22-23高一上·四川凉山·期末)为迎接四川省第十六届少数民族传统运动会,州民族体育场
进行了改造翻新,在改造州民族体育场时需更新所有座椅,并要求座椅的使用年限为15年,已知
每千套座椅建造成本是8万元,设每年的管理费用为 万元与总座椅数 千套,两者满足关系式:
.15年的总维修费用为80万元,记 为15年的总费用.(总费用=建造成本
费用+使用管理费用+总维修费用).请问当设置多少套座椅时,15年的总费用 最小,并求出最
小值.
【答案】 千套时, 取得最小值为180万元
【分析】根据总费用=建造成本费用+使用管理费用+总维修费用,再根据基本不等式求总费用的最
值,并求等号成立的条件.
【详解】由题意得:建造成本费用为 ,
使用管理费: ,所以 ,
,
当且仅当 时,即 千套时, 取得最小值为180万元.
学科网(北京)股份有限公司恒成立问题(共8题)
1.(23-24高一上·陕西汉中·期末)已知函数
(1)若不等式 的解集为 ,求 的值;
(2)若对任意的 恒成立,求实数 的取值范围.
【答案】(1)
(2)
【分析】(1)根据一元二次不等式的解、根与系数关系求得 .
(2)利用分离常数法,结合基本不等式求得 的取值范围.
【详解】(1)原不等式可化为 ,因为该不等式的解集为 ,
可知 的两根为 和 ,
则 ,即 ,解得 ;
所以 .
(2)若对任意的 恒成立,
则对任意的 , 恒成立,
即对任意的 , 恒成立,所以 ,
又因为 , ,
当且仅当 ,即 时取等号,所以 ,
学科网(北京)股份有限公司所以实数 的取值范围是 .
2.(23-24高一上·福建龙岩·期末)已知二次函数 ,对任意 都有
,且 .
(1)求函数 的解析式;
(2)若对于 ,不等式 恒成立,求x的取值范围.
【答案】(1)
(2)
【分析】(1)由题意可得函数 关于 对称,再根据 求出 即可;
(2)不等式 即为 ,将 当作参数,分 , 和
三种情况讨论,利用分离参数法求解即可.
【详解】(1)因为 ,所以函数 关于 对称,
则 ,解得 ,
所以 ;
(2)不等式 即为 ,
当 时,则 恒成立,
而 ,
所以 ,即 ,
因为 ,
所以 ;
学科网(北京)股份有限公司当 时, 恒成立,此时 ;
当 时,则 恒成立,
而 ,
所以 ,解得 ,
综上所述, 的取值范围为 .
3.(23-24高一上·河南郑州·期末)已知函数 .
(1)若不等式 对一切实数x恒成立,求a的取值范围;
(2)解关于x的不等式 .
【答案】(1)
(2)答案见解析
【分析】(1)把恒成立问题转化为 对于一切实数x恒成立,用判别式法列式求
解即可;
(2)分类讨论解一元二次不等式即可.
【详解】(1)由题意,不等式 对于一切实数x恒成立,
等价于 对于一切实数x恒成立,所以 ,
解得 .
(2)不等式 等价于 .
当 即 时,不等式可化为 ,原不等式的解集 ;
当 即 时,不等式可化为 ,原不等式的解集为: ;
当 即 时,不等式可化为 ,此时 .
学科网(北京)股份有限公司综上所述:①当 时,不等式的解集为 ;
②当 时,不等式的解集为 ;
③当 时,不等式的解集为 .
4.(23-24高一上·陕西渭南·期末)设 .
(1)若不等式 对一切实数 恒成立,求实数 的取值范围;
(2)解关于 的不等式 .
【答案】(1)
(2)答案见解析
【分析】(1)讨论a是否为0,不为0时,结合一元二次不等式恒成立列出不等式组,即可求得
答案;
(2)将 化简为 ,分类讨论,比较 的大小,即可得答案.
【详解】(1)不等式 对一切实数 恒成立,即 对一切实数 恒成立,
当 时, 即 ,满足题意;
当 时,需满足 ,解得 ;
故实数 的取值范围为 ;
(2)由 可得 ,即 ,
即
当 ,即 时, 的解集为 ;
当 ,即 时, 的解集为 ;
当 ,即 时, 的解集为 ;
故原不等式的解集为:当 时,解集为 ;
学科网(北京)股份有限公司当 时,解集为 ;
当 ,时,解集为 ;
5.(22-23高一上·天津·期末)已知函数
(1)若 的解集为 ,求实数 的值;
(2)若 对 恒成立,求实数 的取值范围;
(3)若 ,求关于 的不等式 的解集.
【答案】(1) ;
(2) ;
(3)详见解析.
【分析】(1)根据题意,得到 和3为方程 的两根,根据韦达定理,即可得出结
果;
(2)根据题意,得到 恒成立,分别讨论 和 两种情况,即可得出结果;
(3)分 , , , 四种情况讨论结合二次不等式解法可得.
【详解】(1)因为 的解集为 ,
所以 且 和3为方程 的两根,所以 ,
解得 ;
(2) 对 恒成立,
①当 时, ,符合题意;
②当 时, ,解得 ,
学科网(北京)股份有限公司综上,实数a的取值范围是 ;
(3)由 ,得 ,
即 ,
当 时, ,即 ,
当 时, ,
当 时, ,解得 ,
当 时, ,
解得 ,或 ,
当 时, ,
解得 ,或 ,
综上:当 时,原不等式的解集为 ;
当 时,原不等式的解集为 ;
当 时,原不等式的解集为 ,或
当 时,原不等式的解集为 ,或
6.(23-24高一上·云南德宏·期末)已知 .
(1)若 恒成立,求实数 的取值范围;
(2)求不等式 的解集.
【答案】(1)
(2)答案见解析
学科网(北京)股份有限公司【分析】(1)由 恒成立,即 恒成立,即得 ,从而可求解.
(2)由 即 ,然后对 分情况讨论,从而可求解.
【详解】(1)∵ 恒成立,
∴ 对 恒成立,
故 ,化简得 ,解得 ,
故实数 的取值范围 .
(2) ,即 ;
当 时,不等式的解为 或 ,
当 时,不等式的解为 或 ,
当 时,不等式的解为 .
7.(23-24高一上·湖北恩施·期末)已知函数 .
(1)当 时,解关于 的不等式 ;
(2)若不等式 对一切 恒成立,求实数 的取值范围.
【答案】(1)答案见解析
(2)
【分析】(1)先把二次不等式化为 ,然后分类讨论解不等式即可;
(2)参变分离,把恒成立问题转化为 的最大值问题,换元后利用基本不等式求解即可.
【详解】(1)因为 ,
所以不等式 ,
学科网(北京)股份有限公司可化简为: ,
①当 时,不等式化为 ,
②当 即 时, ,
方程 的两个根为 ,1.则不等式的解为 或 ,
③当 即 时, ,
方程 的两个根为 ,1.则不等式的解为 ,
综上所述:当 时,不等式的解集为 ,
当 时,不等式的解集为 ,
当 时,不等式的解集为 .
(2)不等式 即 ,
即 对 恒成立,令 ,所以 ,
因为 ,当且仅当 时取“=”,
所以 ,当且仅当 时取“=”,
所以 的取值范围为 .
8.(22-23高一上·浙江湖州·期末)已知函数 , .
(1)若对任意 ,不等式 恒成立,求m的取值范围;
(2)若对任意 ,存在 ,使得 ,求m的取值范围;
学科网(北京)股份有限公司(3)若 ,对任意 ,总存在 ,使得不等式 成立,求实数k的取
值范围.
【答案】(1)
(2)
(3)
【分析】(1)将不等式 恒成立转化为 恒成立,再根据 即可求
m的取值范围;
(2)将题中条件转化为 的值域包含于 的值域,再根据区间 的两端点的函数值
可得到 的对称轴 在区间 之间,从而可得到 ,进而可求得
m的取值范围;
(3)将不等式 成立化简得到不等式 成立,再构造函数
,从而得到 ,再构造函数 ,根据
即可求解.
【详解】(1)由题意得 恒成立,
得 恒成立,即
解得 .
(2)当 ,当 ,
由题意得
学科网(北京)股份有限公司∴ 得 ,
此时 对称轴为 ,
故 ,即 得 或 ,
综上可得 .
(3)由题意得对任意 ,总存在 ,使得不等式 成立,
令 ,由题意得 ,
而 ,
设 ,则 ,
而 ,
易得 ,故 .
【点睛】关键点点睛:小问(2)的关键是将题中条件转化为 的值域包含于 的值域,再
根据闭区间的端点和函数的对称轴来求解参数的取值范围;小问(3)的关键是构造函数,即将不
等式成立问题转化为求解函数的最值问题.
学科网(北京)股份有限公司