文档内容
2024 届云南三校高考备考实用性联考卷(二)
数学
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填
写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮
擦干净后,再选涂其他答案标号.在试题卷上作答无效.
3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
1. 已知集合 , ,则 ( ).
A. B.
C. D.
2. 若复数 , ,则 ( ).
A. B. 0 C. 1 D. 2
3. 已知 ,且 ,则下列结果正确的是( ).
A. B.
C. D.
4. 记 为等差数列 的前n项和.若 , ,则 ( ).
A. 25 B. 22 C. 20 D. 15
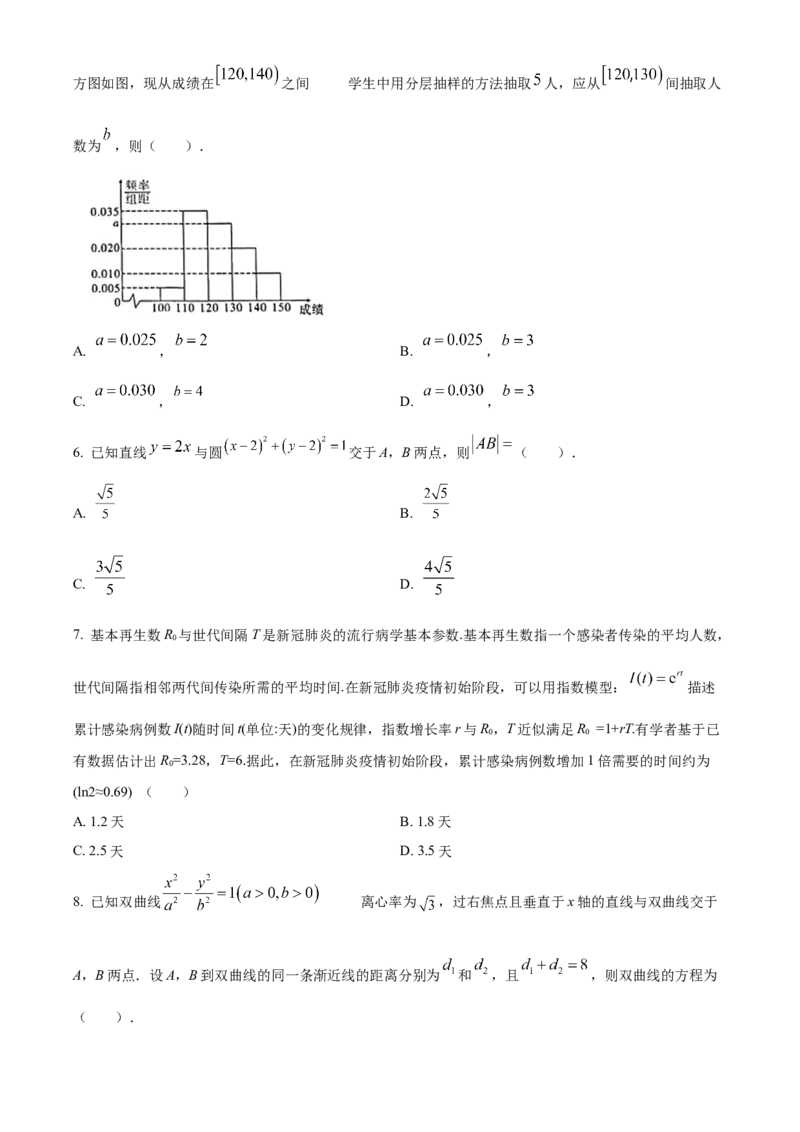
5. 要调查某地区高中学生身体素质,从高中生中抽取 人进行跳远测试,根据测试成绩制作频率分布直方图如图,现从成绩在 之间 的学生中用分层抽样的方法抽取 人,应从 间抽取人
数为 ,则( ).
A. , B. ,
C. , D. ,
6. 已知直线 与圆 交于A,B两点,则 ( ).
A. B.
C. D.
7. 基本再生数R 与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,
0
世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型: 描述
累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R,T近似满足R =1+rT.有学者基于已
0 0
有数据估计出R=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为
0
(ln2≈0.69) ( )
A. 1.2天 B. 1.8天
C. 2.5天 D. 3.5天
8. 已知双曲线 的离心率为 ,过右焦点且垂直于x轴的直线与双曲线交于
A,B两点.设A,B到双曲线的同一条渐近线的距离分别为 和 ,且 ,则双曲线的方程为
( ).A. B.
C. D.
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有
多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)
9. 已知随机变量 且 ,随机变量 ,若 ,则(
).
A. B.
C. D.
10. 已知 , , 是 导函数,则( ).
的
A. 是由 图象上的点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向左平移 个
单位长度得到的
B. 是由 图象上的点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移 个
单位长度得到的
C. 的对称轴方程为 ,
D. 是 的一条切线方程
11. 已知偶函数 对 ,都有 ,且 时, ,下列
结论正确的是( ).
A. 函数 的图象关于点 中心对称B. 是周期为4的函数
C.
D.
12. 已知过点 的直线l与抛物线 交于A,B两点,O为坐标原点,且 于点D,直线
, 的斜率分别为 , ,则( ).
A. B.
C. 点D的轨迹是椭圆 D.
三、填空题(本大题共4小题,每小题5分,共20分)
13. 已知平面向量 , 满足 ,且 ,则 与 的夹角为__________.
14. 设 ,若 与 的二项展开式中的常数项相等,则 ________
15. 圆锥 的底面半径为1,其侧面展开图是圆心角大小为 的扇形,正四棱柱 的
上底面的顶点 , , , 均在圆锥 的侧面上,棱柱下底面在圆锥 的底面上,则此正四棱柱体
积的最大值为__________.
16. 已知函数 ,若 与 的图象有且仅有一个公共点,则k的取值范围是
______.
四、解答题(共70分,解答应写出文字说明,证明过程或演算步骤)
17. 在正项数列 中,已知 , .
(1)求数列 的通项公式;(2)设数列 的前n项积为 ,求 取得最大值时 的取值.
18. 已知 的三个内角A,B,C对应的三条边分别为a,b,c,且有: .
(1)求角B的大小;
(2)设 ,若点M是边 上一点,且 , ,求 的面积.
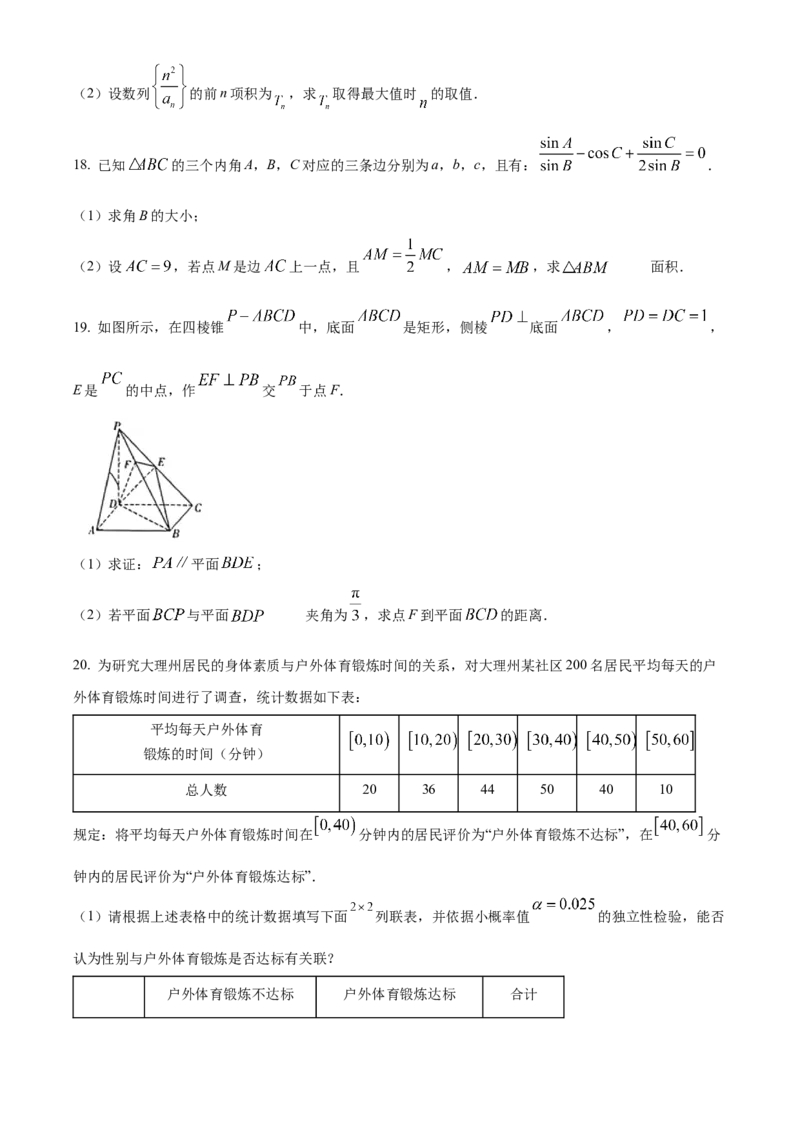
19. 如图所示,在四棱锥 中,底面 是矩形,侧棱 底面 , ,
E是 的中点,作 交 于点F.
(1)求证: 平面 ;
(2)若平面 与平面 的夹角为 ,求点F到平面 的距离.
20. 为研究大理州居民的身体素质与户外体育锻炼时间的关系,对大理州某社区200名居民平均每天的户
外体育锻炼时间进行了调查,统计数据如下表:
平均每天户外体育
锻炼的时间(分钟)
总人数 20 36 44 50 40 10
规定:将平均每天户外体育锻炼时间在 分钟内的居民评价为“户外体育锻炼不达标”,在 分
钟内的居民评价为“户外体育锻炼达标”.
(1)请根据上述表格中的统计数据填写下面 列联表,并依据小概率值 的独立性检验,能否
认为性别与户外体育锻炼是否达标有关联?
户外体育锻炼不达标 户外体育锻炼达标 合计男
女 20 110
合计
(2)从上述“户外体育锻炼不达标”的居民中,按性别用分层抽样的方法抽取5名居民,再从这5名居民中
随机抽取3人了解他们户外体育锻炼时间偏少的原因,记所抽取的3人中男性居民的人数为随机变量X,
求X的分布列和数学期望;
(3)将上述调查所得到的频率视为概率来估计全州的情况,现在从全州所有居民中随机抽取4人,求其中
恰好有2人“户外体育锻炼达标”的概率.
参考公式: ,其中 .
参考数据:( 独立性检验中常用的小概率值和相应的临界值)
0.10 0.05 0.025 0.010
2.706 3.841 5.024 6.635
21. 已知 .
(1)当 时,求 在 上的单调性;
(2)若 ,令 ,讨论方程 的解的个数.
22. 已知圆 ,直线 过点 且与圆 交于点B,C,线段 的中点为D,过
的中点E且平行于 的直线交 于点P.
(1)求动点P的轨迹方程;
(2)坐标原点O关于 , 的对称点分别为 , ,点 , 关于直线 的对称点分别为 ,
,过 的直线 与动点P的轨迹交于点M,N,直线 与 相交于点Q.求证: 的面积是定值.2024 届云南三校高考备考实用性联考卷(二)
数学
注意事项:
1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填
写清楚.
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮
擦干净后,再选涂其他答案标号.在试题卷上作答无效.
3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只
有一项是符合题目要求的)
【1题答案】
【答案】A
【2题答案】
【答案】C
【3题答案】
【答案】B
【4题答案】
【答案】C
【5题答案】
【答案】D
【6题答案】
【答案】B
【7题答案】
【答案】B
【8题答案】
【答案】A
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有
多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分)
【9题答案】
【答案】ABC
【10题答案】【答案】BC
【11题答案】
【答案】ACD
【12题答案】
【答案】AB
三、填空题(本大题共4小题,每小题5分,共20分)
【13题答案】
【答案】
【14题答案】
【答案】4
【15题答案】
【答案】 ##
【16题答案】
【答案】 或
四、解答题(共70分,解答应写出文字说明,证明过程或演算步骤)
【17题答案】
【答案】(1)
(2) 或
【18题答案】
【答案】(1)
(2)
【19题答案】
【答案】(1)证明见解析(2)
【20题答案】
【答案】(1)表格见解析,有关联
(2)分布列见解析,
(3)
【21题答案】
【答案】(1) 在 上递增
(2)答案见解析
【22题答案】
【答案】(1)
(2)证明见解析