文档内容
关注精品公众号【偷着学】或添加微信:tzx985tzx
绝密★本科目考试启用前
2024 年普通高等学校招生全国统一考试(北京卷)
数学
本试卷共12页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.
考试结束后,将本试卷和答题卡一并交回.
第一部分(选择题 共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要
求的一项.
1. 已知集合 , ,则 ( )
A. B.
C. D.
2. 已知 ,则 ( ).
A. B. C. D.
3. 圆 的圆心到直线 的距离为( )
A. B. C. D.
4. 在 的展开式中, 的系数为( )
A. B. C. D.
5. 设 , 是向量,则“ ”是“ 或 ”的( ).
.
A 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
6. 设函数 .已知 , ,且 的最小值为 ,则 (
)关注精品公众号【偷着学】或添加微信:tzx985tzx
A. 1 B. 2 C. 3 D. 4
7. 生物丰富度指数 是河流水质的一个评价指标,其中 分别表示河流中的生物种类数与生物
个体总数.生物丰富度指数d越大,水质越好.如果某河流治理前后的生物种类数 没有变化,生物个体总
数由 变为 ,生物丰富度指数由 提高到 ,则( )
A. B.
C. D.
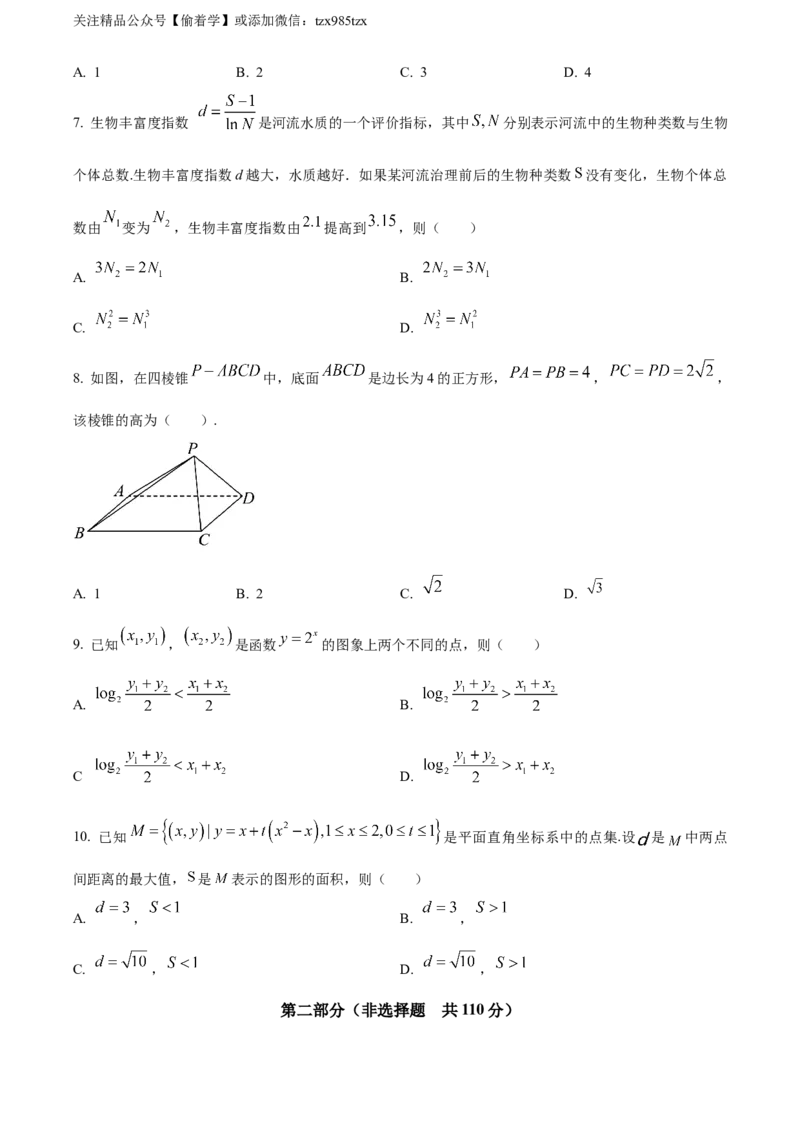
8. 如图,在四棱锥 中,底面 是边长为4的正方形, , ,
该棱锥的高为( ).
A. 1 B. 2 C. D.
9. 已知 , 是函数 的图象上两个不同的点,则( )
A. B.
.
C D.
10. 已知 是平面直角坐标系中的点集.设 是 中两点
间距离的最大值, 是 表示的图形的面积,则( )
A. , B. ,
C. , D. ,
第二部分(非选择题 共110分)关注精品公众号【偷着学】或添加微信:tzx985tzx
二、填空题共5小题,每小题5分,共25分.
11. 抛物线 的焦点坐标为________.
12. 在平面直角坐标系 中,角 与角 均以 为始边,它们的终边关于原点对称.若 ,
则 的最大值为________.
13. 若直线 与双曲线 只有一个公共点,则 的一个取值为 ________.
14. 汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中升量器、斗量器、斛量器
的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直径依次为
,且斛量器的高为 ,则斗量器的高为______ ,升量器的高为
________ .
15. 设 与 是两个不同的无穷数列,且都不是常数列.记集合 ,给出下列
4个结论:
①若 与 均为等差数列,则M中最多有1个元素;
②若 与 均为等比数列,则M中最多有2个元素;
③若 为等差数列, 为等比数列,则M中最多有3个元素;
④若 为递增数列, 为递减数列,则M中最多有1个元素.
其中正确结论的序号是______.
三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.
16. 在 中,内角 的对边分别为 , 为钝角, , .
(1)求 ;
的
(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得 存在,求 面积.关注精品公众号【偷着学】或添加微信:tzx985tzx
条件①: ;条件②: ;条件③: .
注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解
答计分.
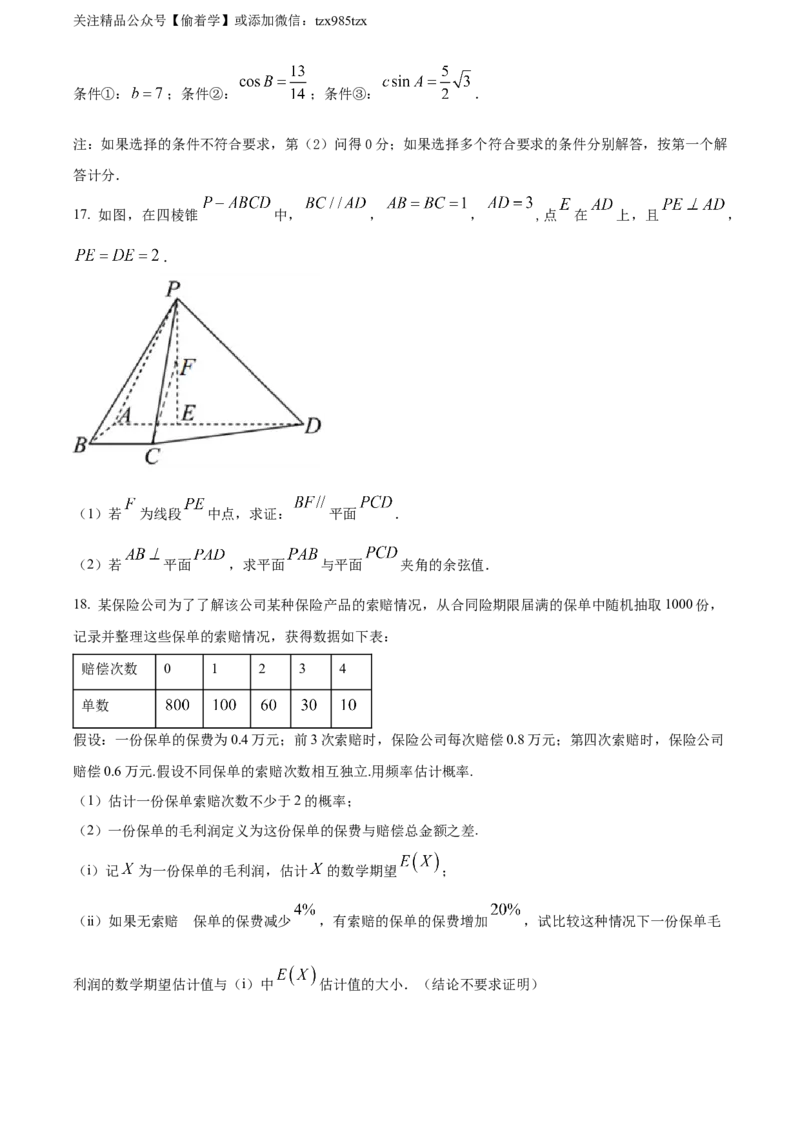
17. 如图,在四棱锥 中, , , ,点 在 上,且 ,
.
(1)若 为线段 中点,求证: 平面 .
(2)若 平面 ,求平面 与平面 夹角的余弦值.
18. 某保险公司为了了解该公司某种保险产品的索赔情况,从合同险期限届满的保单中随机抽取1000份,
记录并整理这些保单的索赔情况,获得数据如下表:
赔偿次数 0 1 2 3 4
单数
假设:一份保单的保费为0.4万元;前3次索赔时,保险公司每次赔偿0.8万元;第四次索赔时,保险公司
赔偿0.6万元.假设不同保单的索赔次数相互独立.用频率估计概率.
(1)估计一份保单索赔次数不少于2的概率;
(2)一份保单的毛利润定义为这份保单的保费与赔偿总金额之差.
(i)记 为一份保单的毛利润,估计 的数学期望 ;
的
(ⅱ)如果无索赔 保单的保费减少 ,有索赔的保单的保费增加 ,试比较这种情况下一份保单毛
利润的数学期望估计值与(i)中 估计值的大小.(结论不要求证明)关注精品公众号【偷着学】或添加微信:tzx985tzx
19. 已知椭圆 : ,以椭圆 的焦点和短轴端点为顶点的四边形是边长为2的正
方形.过点 且斜率存在的直线与椭圆 交于不同的两点 ,过点 和 的直线
与椭圆 的另一个交点为 .
的
(1)求椭圆 方程及离心率;
(2)若直线BD的斜率为0,求t的值.
20. 设函数 ,直线 是曲线 在点 处的切线.
(1)当 时,求 的单调区间.
(2)求证: 不经过点 .
(3)当 时,设点 , , , 为 与 轴的交点, 与
分别表示 与 的面积.是否存在点 使得 成立?若存在,这样的点 有
几个?
(参考数据: , , )
21. 已知集合 .给定数
列 ,和序列 ,其中 ,对数列 进行如
下变换:将 的第 项均加1,其余项不变,得到的数列记作 ;将 的第 项
均加1,其余项不变,得到数列记作 ;……;以此类推,得到 ,简记为 .
(1)给定数列 和序列 ,写出 ;
(2)是否存在序列 ,使得 为 ,若存在,
写出一个符合条件的 ;若不存在,请说明理由;关注精品公众号【偷着学】或添加微信:tzx985tzx
(3)若数列 的各项均为正整数,且 为偶数,求证:“存在序列 ,使得 的各项
都相等”的充要条件为“ ”.