文档内容
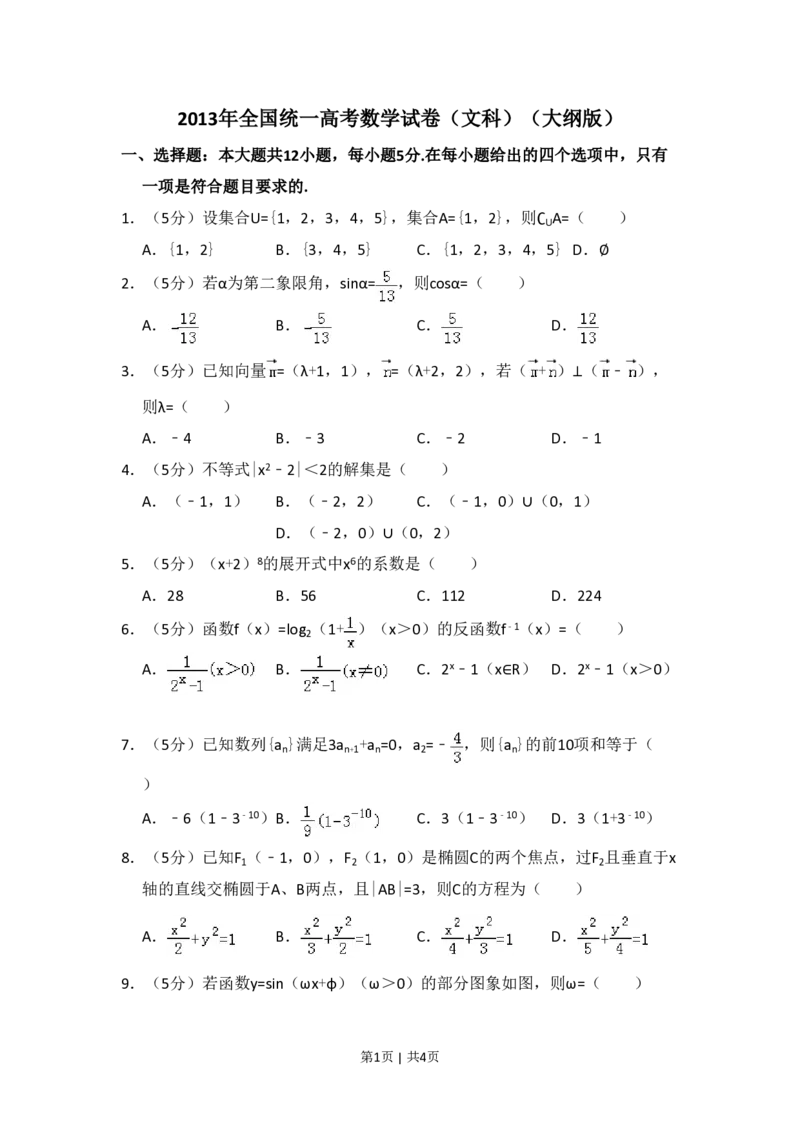
2013年全国统一高考数学试卷(文科)(大纲版)
一、选择题:本大题共12小题,每小题5分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.(5分)设集合U={1,2,3,4,5},集合A={1,2},则∁ A=( )
U
A.{1,2} B.{3,4,5} C.{1,2,3,4,5} D.∅
2.(5分)若α为第二象限角,sinα= ,则cosα=( )
A. B. C. D.
3.(5分)已知向量 =(λ+1,1), =(λ+2,2),若( + )⊥( ﹣ ),
则λ=( )
A.﹣4 B.﹣3 C.﹣2 D.﹣1
4.(5分)不等式|x2﹣2|<2的解集是( )
A.(﹣1,1) B.(﹣2,2) C.(﹣1,0)∪(0,1)
D.(﹣2,0)∪(0,2)
5.(5分)(x+2)8的展开式中x6的系数是( )
A.28 B.56 C.112 D.224
6.(5分)函数f(x)=log (1+ )(x>0)的反函数f﹣1(x)=( )
2
A. B. C.2x﹣1(x∈R) D.2x﹣1(x>0)
7.(5分)已知数列{a }满足3a +a =0,a =﹣ ,则{a }的前10项和等于(
n n+1 n 2 n
)
A.﹣6(1﹣3﹣10)B. C.3(1﹣3﹣10) D.3(1+3﹣10)
8.(5分)已知F (﹣1,0),F (1,0)是椭圆C的两个焦点,过F 且垂直于x
1 2 2
轴的直线交椭圆于A、B两点,且|AB|=3,则C的方程为( )
A. B. C. D.
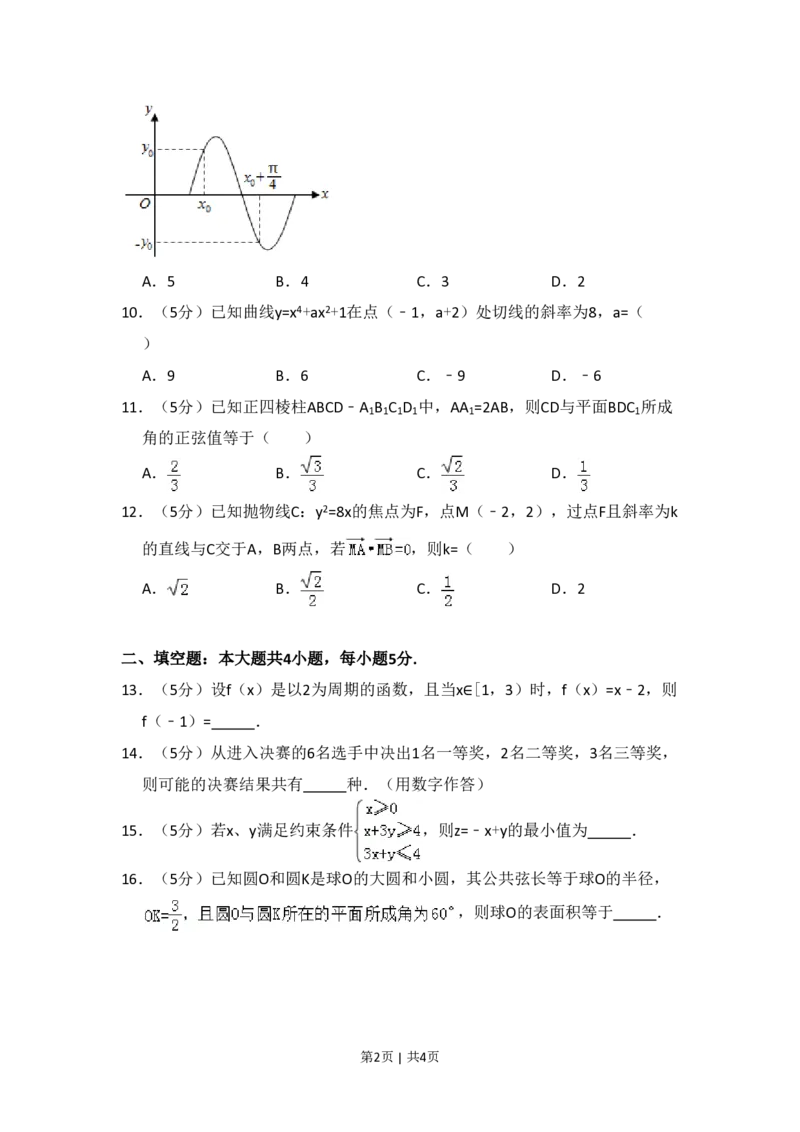
9.(5分)若函数y=sin(ωx+φ)(ω>0)的部分图象如图,则ω=( )
第1页 | 共4页A.5 B.4 C.3 D.2
10.(5分)已知曲线y=x4+ax2+1在点(﹣1,a+2)处切线的斜率为8,a=(
)
A.9 B.6 C.﹣9 D.﹣6
11.(5分)已知正四棱柱ABCD﹣A B C D 中,AA =2AB,则CD与平面BDC 所成
1 1 1 1 1 1
角的正弦值等于( )
A. B. C. D.
12.(5分)已知抛物线C:y2=8x的焦点为F,点M(﹣2,2),过点F且斜率为k
的直线与C交于A,B两点,若 ,则k=( )
A. B. C. D.2
二、填空题:本大题共4小题,每小题5分.
13.(5分)设f(x)是以2为周期的函数,且当x∈[1,3)时,f(x)=x﹣2,则
f(﹣1)= .
14.(5分)从进入决赛的6名选手中决出1名一等奖,2名二等奖,3名三等奖,
则可能的决赛结果共有 种.(用数字作答)
15.(5分)若x、y满足约束条件 ,则z=﹣x+y的最小值为 .
16.(5分)已知圆O和圆K是球O的大圆和小圆,其公共弦长等于球O的半径,
,则球O的表面积等于 .
第2页 | 共4页三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(10分)等差数列{a }中,a =4,a =2a ,
n 7 19 9
(Ⅰ)求{a }的通项公式;
n
(Ⅱ)设b = ,求数列{b }的前n项和S .
n n n
18.(12分)设△ABC的内角A,B,C的内角对边分别为a,b,c,满足(a+b+c
)(a﹣b+c)=ac.
(Ⅰ)求B.
(Ⅱ)若sinAsinC= ,求C.
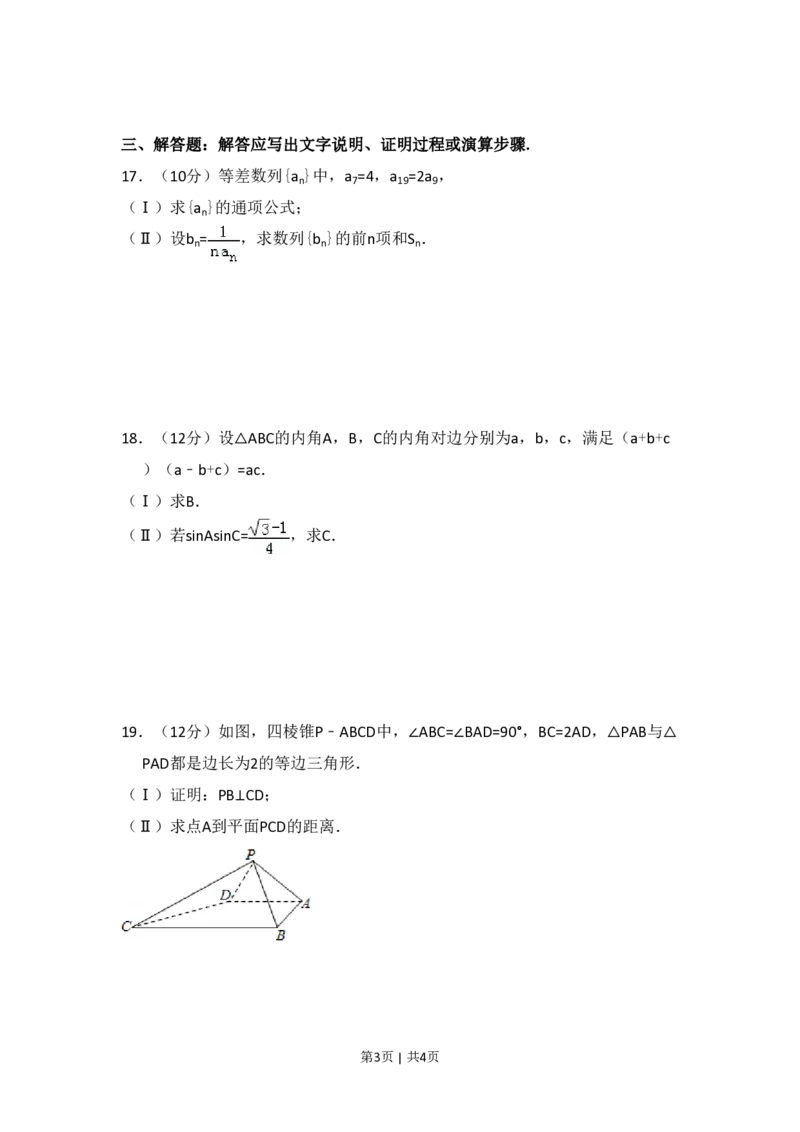
19.(12分)如图,四棱锥P﹣ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△
PAD都是边长为2的等边三角形.
(Ⅰ)证明:PB⊥CD;
(Ⅱ)求点A到平面PCD的距离.
第3页 | 共4页20.(12分)甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁
判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率
均为 ,各局比赛的结果都相互独立,第1局甲当裁判.
(Ⅰ)求第4局甲当裁判的概率;
(Ⅱ)求前4局中乙恰好当1次裁判概率.
21.(12分)已知函数f(x)=x3+3ax2+3x+1.
(Ⅰ)求a= 时,讨论f(x)的单调性;
(Ⅱ)若x∈[2,+∞)时,f(x)≥0,求a的取值范围.
22.(12分)已知双曲线C: =1(a>0,b>0)的左、右焦点分别为F
1
,F ,离心率为3,直线y=2与C的两个交点间的距离为 .
2
(I)求a,b;
(II)设过F 的直线l与C的左、右两支分别相交于A、B两点,且|AF |=|BF |,证
2 1 1
明:|AF |、|AB|、|BF |成等比数列.
2 2
第4页 | 共4页