第Ⅰ卷
一.选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，
只有一项是符合题目要求的.
1．若数z =i(-2-i) (i为虚数单位) 在复平面内所对应的点在
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．若集合A= xÎR ax2 +ax+1 中只有一个元素，则a=（ ）
A．4 B． 2 C．0 D．0或4
a 3
3.若sin = ，则cosa=（ ）
2 3
2 1 1 2
A．- B．- C ． D．
3 3 3 3
4.若集合A=2,3，B=1,2,3，从A，B中各任意取一个数，则这两数之和等于4的
概率是
2 1 1 1
A． B． C． D．
3 2 3 6
5.总体由编号01，,02，…，19,20的20个个体组成。利用下面的随机数表选取5个个
体，选取方法是随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，
则选出来的第5个个体的编号为
7816 6572 0802 6314 0702 4369 9728 0198
第1页 | 共6页3204 9234 4935 8200 3623 4869 6938 7481
A．08 B．07 C．02 D．01
A.08 B.07 C.02 D.01
1
6．下列选项中，使x< < x2成立的x的取值范围是（ ）
x
A．(-¥,-1) B．(-1,0) C． (0,1) D．(1,+¥)
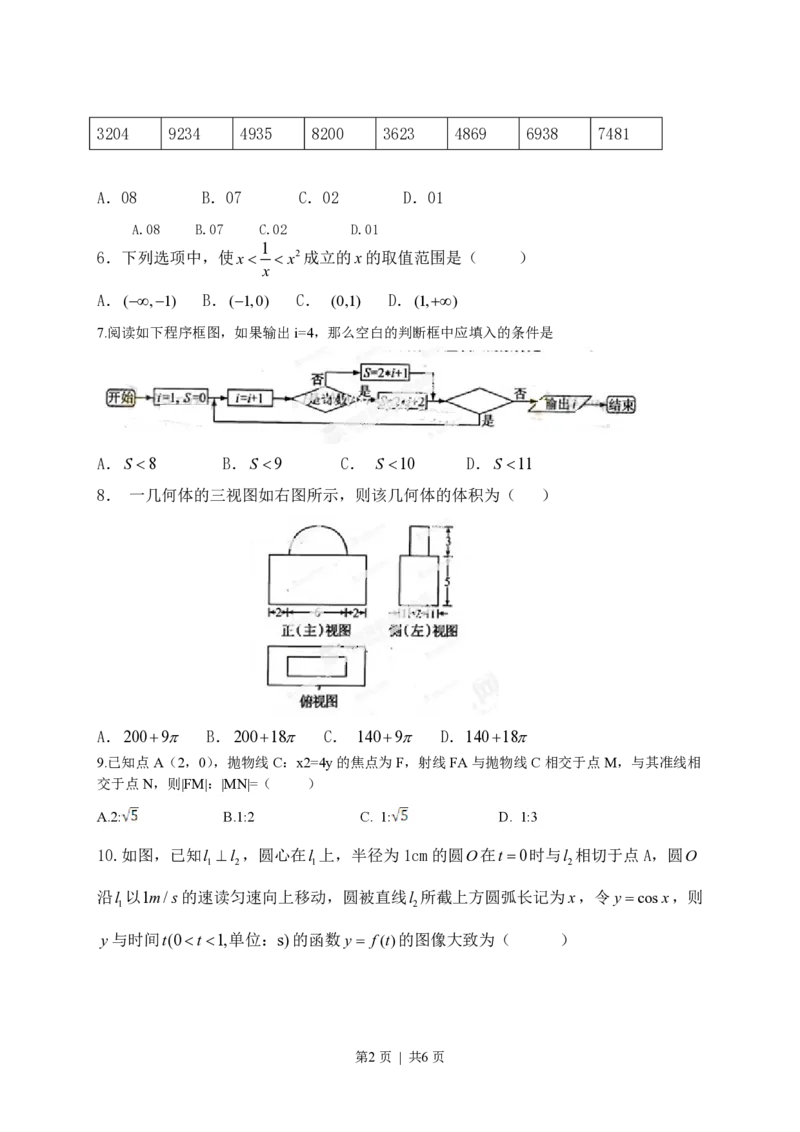
7.阅读如下程序框图，如果输出i=4，那么空白的判断框中应填入的条件是
A．S <8 B．S <9 C． S <10 D．S <11
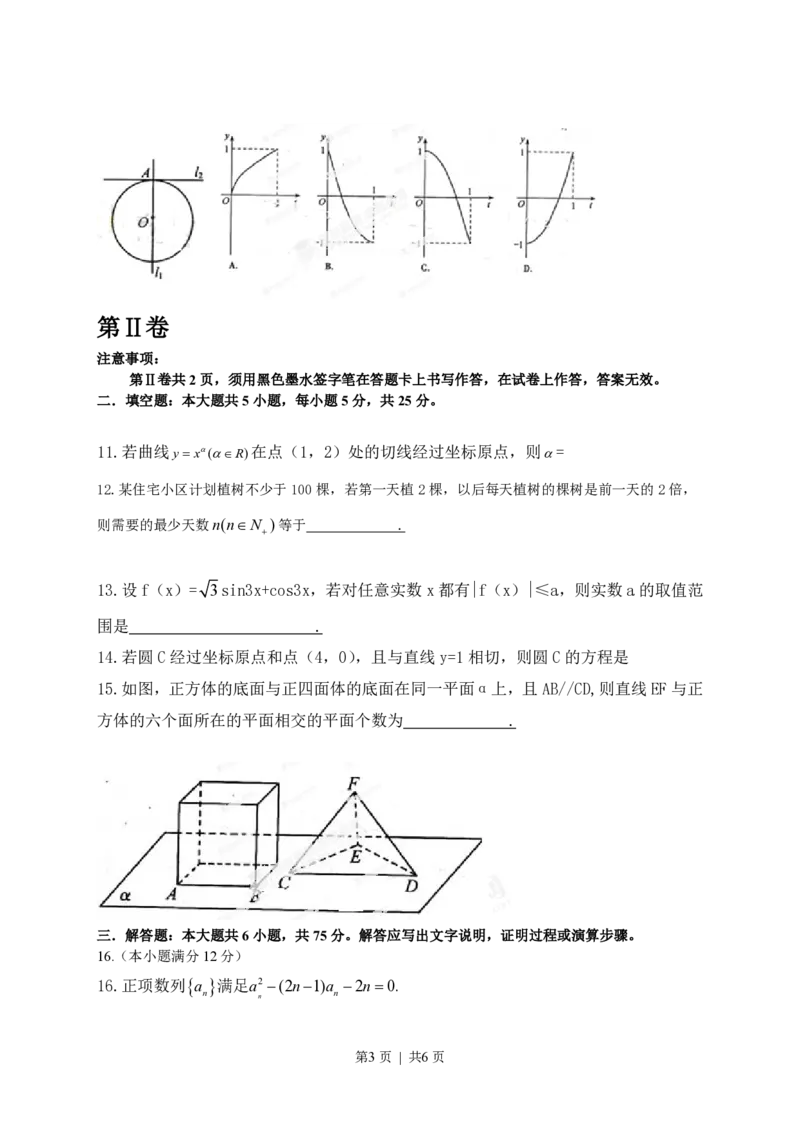
8． 一几何体的三视图如右图所示，则该几何体的体积为（ ）
A．200+9p B．200+18p C． 140+9p D．140+18p
9.已知点A（2，0），抛物线C：x2=4y的焦点为F，射线FA与抛物线C相交于点M，与其准线相
交于点 N， 则|FM |：|MN|=（ ）
A.2: B.1:2 C. 1: D. 1:3
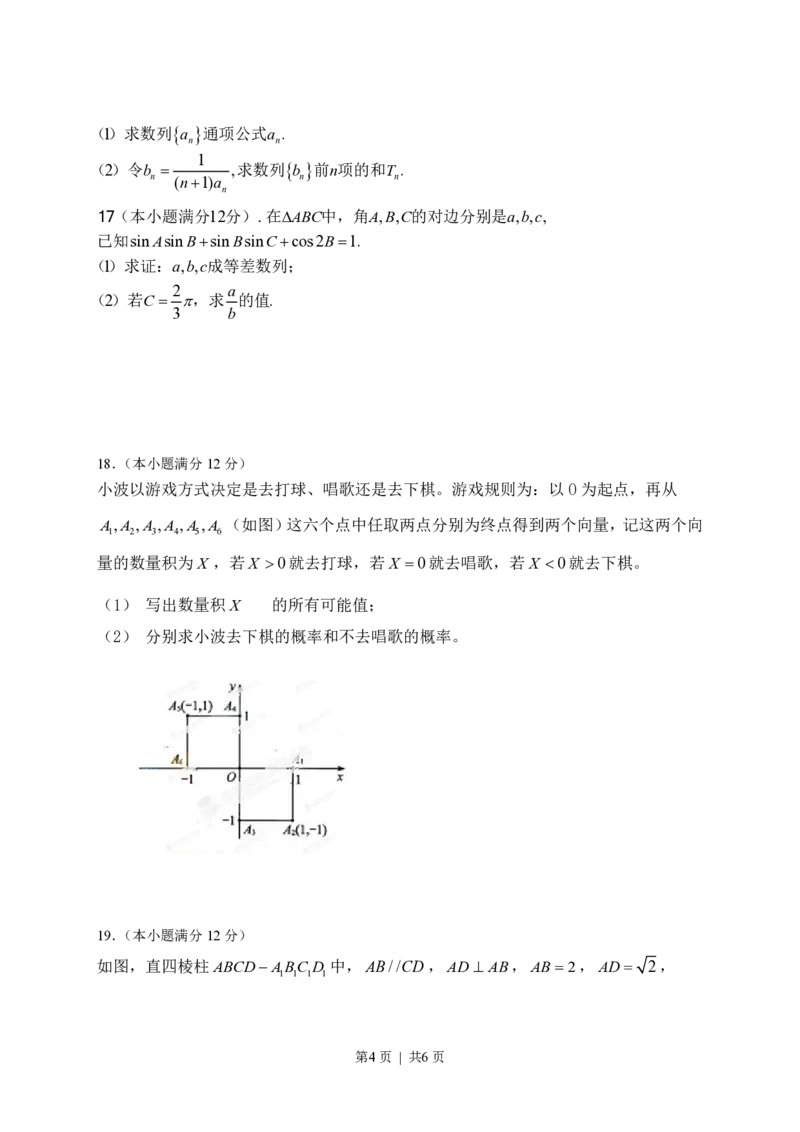
10.如图，已知l ^l ，圆心在l 上，半径为1cm的圆O在t =0时与l 相切于点A，圆O
1 2 1 2
沿l 以1m/s的速读匀速向上移动，圆被直线l 所截上方圆弧长记为x，令y =cosx，则
1 2
y与时间t(0<t <1,单位：s)的函数y = f(t)的图像大致为（ ）
第2页 | 共6页第Ⅱ卷
注意事项：
第Ⅱ卷共2页，须用黑色墨水签字笔在答题卡上书写作答，在试卷上作答，答案无效。
二．填空题：本大题共5小题，每小题5分，共25分。
11.若曲线y=x(ÎR)在点（1，2）处的切线经过坐标原点，则=
12.某住宅小区计划植树不少于100棵，若第一天植2棵，以后每天植树的棵树是前一天的2倍，
则需要的最少天数n(nÎN )等于 .
+
13.设f（x）= 3sin3x+cos3x，若对任意实数x都有|f（x）|≤a，则实数a的取值范
围是 .
14.若圆C经过坐标原点和点（4，0），且与直线y=1相切，则圆C的方程是
15.如图，正方体的底面与正四面体的底面在同一平面α上，且AB//CD,则直线EF与正
方体的六个面所在的平面相交的平面个数为 .
三．解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。
16.（本小题满分12分）
16.正项数列a 满足a2 -(2n-1)a -2n=0.
n n
n
第3页 | 共6页（1）求数列a 通项公式a .
n n
1
（2）令b = ,求数列b 前n项的和T .
n (n+1)a n n
n
17（本小题满分12分）.在ABC中，角A,B,C的对边分别是a,b,c,
已知sin AsinB+sinBsinC+cos2B=1.
（1）求证：a,b,c成等差数列；
2 a
（2）若C = p，求 的值.
3 b
18．（本小题满分12分）
小波以游戏方式决定是去打球、唱歌还是去下棋。游戏规则为：以O为起点，再从
A,A ,A ,A ,A ,A （如图）这六个点中任取两点分别为终点得到两个向量，记这两个向
1 2 3 4 5 6
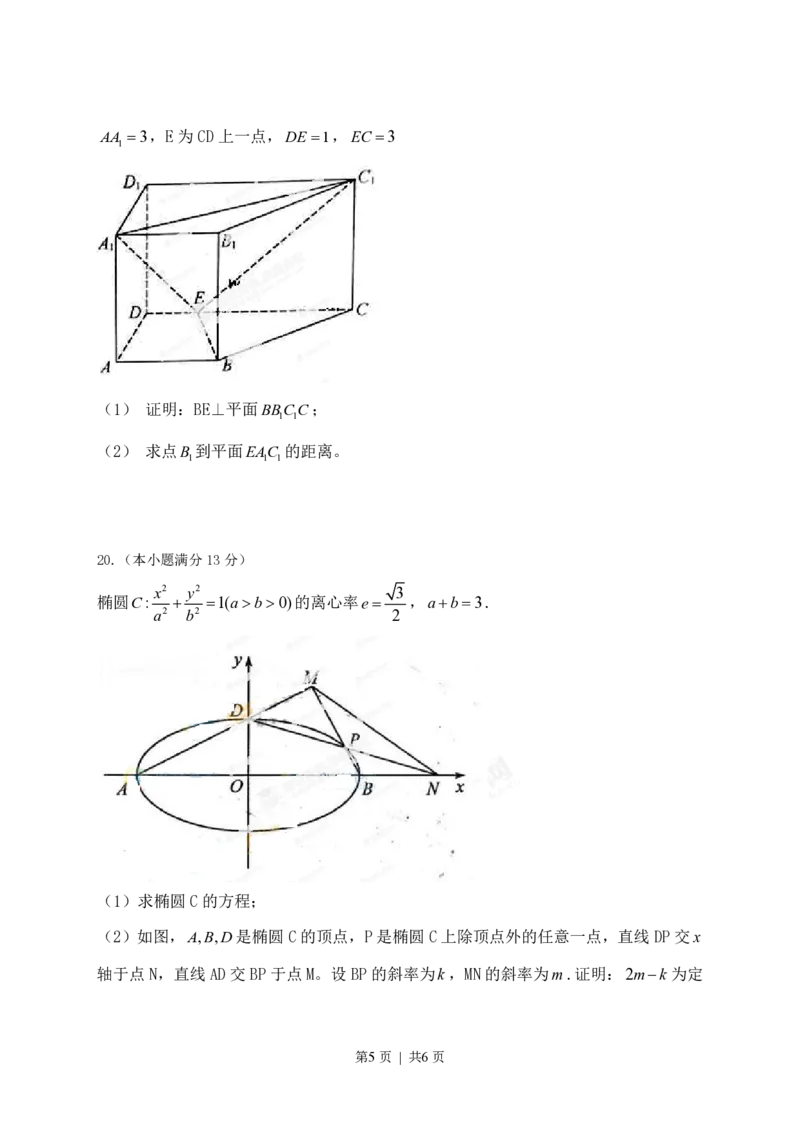
量的数量积为X ，若X >0就去打球，若X =0就去唱歌，若X <0就去下棋。
（1） 写出数量积X 的所有可能值；
（2） 分别求小波去下棋的概率和不去唱歌的概率。
19．（本小题满分12分）
如图，直四棱柱ABCD-ABC D 中，AB//CD，AD^ AB，AB =2，AD= 2，
1 1 1 1
第4页 | 共6页AA =3，E为CD上一点，DE =1，EC =3
1
（1） 证明：BE⊥平面BBCC；
1 1
（2） 求点B 到平面EAC 的距离。
1 1 1
20.（本小题满分13分）
x2 y2 3
椭圆C: + =1(a>b>0)的离心率e= ，a+b=3.
a2 b2 2
（1）求椭圆C的方程；
（2）如图，A,B,D是椭圆C的顶点，P是椭圆C上除顶点外的任意一点，直线DP交x
轴于点N，直线AD交BP于点M。设BP的斜率为k，MN的斜率为m.证明：2m-k 为定
第5页 | 共6页值。
21.（本小题满分14分）
1
x, 0 xa.
a
设函数 f(x)= .a为常数且aÎ(0,1)
1
(1-x),a< x1.
1-a
1 1
（1）当a= 时，求 f(f( ))；
2 3
（2）若x 满足 f(f(x ))= x ，但 f(x)¹0，则称x 为 f(x)的二阶周期点.证明函数 f(x)
0 0 0 0
有且仅有两个二阶周期点，并求二阶周期点x ,x ；
1 2
（3）对于（2）中的x ,x ，设A(x , f(f(x ))),B(x , f(f(x ))),C(a2,0)，记 ABC的面积
1 2 1 1 2 2 V
é1 1ù
为S(a)，求S(a)在区间 , 上的最大值和最小值。
ê ú
ë3 2û
第6页 | 共6页
