2013年高考数学试卷（理）（江西）（解析卷）_数学历年高考真题_新·PDF版2008-2025·高考数学真题_数学（按试卷类型分类）2008-2025_自主命题卷·数学（2008-2025）

第Ⅰ卷（选择题 共50分） 一.选择题：本大题共10小题。每小题5分，共50分。在每个小题给出的四个选项中， 只有一项是符合题目要求的. 1.设集合M={1，2，zi},i为虚数单位，N=｛3，4｝，M∩N=｛4｝，则复数z= （ ） A. -2i B. 2i C. -4i D.4i 2.函数y  xln(1x)的定义域为 （ ） A.(0,1) B.[0,1) C.(0,1] D.[0,1] 【答案】B x0 【解析】  y  xln(1x)， ,0 x1,选B. 1x0 【学科网考点定位】该题主要考查函数的概念、定义域及其求法. 第1页 | 共14页3.等比数列x，3x+3，6x+6，…的的第四项等于 （ ） A.-24 B.0 C.12 D.24 4.总体由编号为01，02，…，19，20的20个个体组成.利用下面的随机数表选取5个 个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数 字，则选出来的第5个个体的编号为 （ ） 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4934 8200 3623 4869 6938 7481 A.08 B.07 C.02 D.01 1 5.(x2  )5展开式中的常数项为（ ） x3 A．80 B.-80 C.40 D.-40 【答案】C 【解析】 T Cr(2)rx105r,令105r=0，得r 2,常数项为C2(2)2=40.选C.  r1 5 5 【学科网考点定位】本题主要考查二项式定理、二项展开式的应用. 2 21 2 6.S  x2dx,S  dx,S  exdx,若 ，则s,s ,s 的大小关系为（ ） 1 1 2 1 x 3 1 1 2 3 A. s＜s＜s s＜s＜s s＜s＜s s＜s＜s 1 2 3 B. 2 1 3 C. 2 3 1 D. 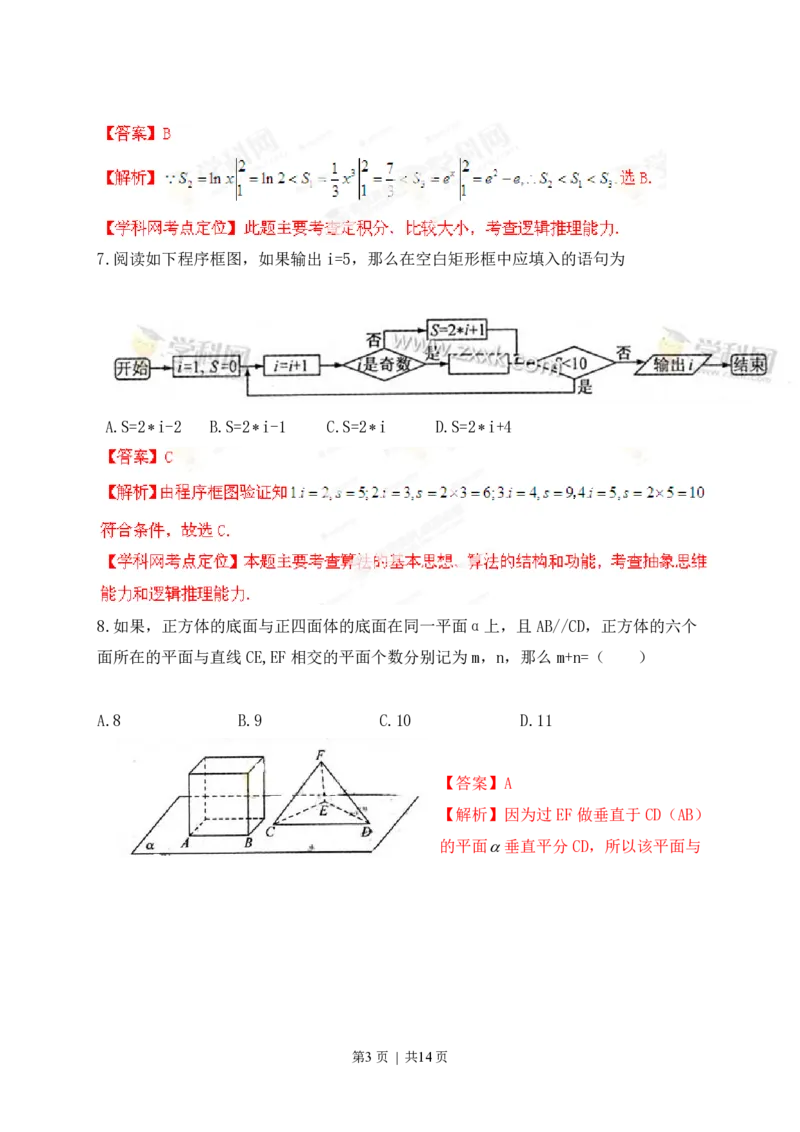3 2 1 第2页 | 共14页7.阅读如下程序框图，如果输出i=5，那么在空白矩形框中应填入的语句为 A.S=2i-2 B.S=2i-1 C.S=2i D.S=2i+4 8.如果，正方体的底面与正四面体的底面在同一平面α上，且AB//CD，正方体的六个 面所在的平面与直线CE,EF相交的平面个数分别记为m，n，那么m+n=（ ） A.8 B.9 C.10 D.11 【答案】A 【解析】因为过EF做垂直于CD（AB） 的平面垂直平分CD，所以该平面与 第3页 | 共14页9.过点（ ，0）引直线ι与曲线y  1x2 交于A,B两点 ，O为坐标原点，当△AOB 的面积取最大值时，直线ι的斜率等于（ ） A. B.- C. D- 10.如图，半径为1的半圆O与等边三角形ABC夹在两平行线ι ，ι 之间，ι//ι ，ι 1 2 1 与半圆相交于F,G两点，与三角形ABC两边相交于E,D两点。 设弧FG的长为x(0＜x＜π),y=EB+BC+CD，若ι从ι 平行移动到ι，则函数y=f(x)的 1 2 图像 大致是 第4页 | 共14页第Ⅱ卷 二．填空题：本大题共 4 小题，每小题 5 分，共 20 分 11．函数y=sin2x+2 sin2x的最小正周期T为_______. 12．设e，e 为单位向量。且e、e 的夹角为 ，若a=e +3e，b=2e，则向量a在b 1 2 1 2 1 2 1 方向上的射影为________. 5 【答案】 2 第5页 | 共14页13．设函数f(x)在（0，+∞）内可导，且f(ex)=x+ex，则 f(1) =__________. 14．抛物线x2=2py（p＞0）的焦点为F，其准线与双曲线 - =1相交于A，B两点， 若△ABF为等边三角形，则p=___________. 三．选做题：请在下列两题中任选一题作答，若两题都做按其中一题评阅计分。本题 共 5 分。 15（1）．（坐标系与参数方程选做题）设曲线C的参数方程为：x=t，y=t2 （t为参数）， 若以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标 方程为_______. 第6页 | 共14页（2）（不等式选做题）在实数范围内，不等式 x2 1 1的解集为___________. 四．解答题：本大题共 6 小题，共 75 分.解答应写出文字说明、证明过程或演算步 骤. 16．（本小题满分12分） 在△ABC中，角A，B，C所对的边分别为a，b，c，已知 cosC(cosA 3sin A)cosB0. （1）求角B的大小； （2）若a+c=1，求b的取值范围. 第7页 | 共14页【学科网考点定位】本题主要考查解三角形、正余弦定理、基本不等式等基础知识，考 查分析问题解决问题的能力. 17．（本小题满分12分） 正项数列{a}的前n项和S 满足：S2 (n2 n1)S (n2 n)0 n n n n （1）求数列{a}的通项公式a； n n n1 （2）令b  ，数列{b}的前n项和为T ．证明：对于任意n Î N*，都有T＜ n (n2)2a2 n n n n 5 . 64 18.（本小题满分12分） 小波以游戏方式决定是参加学校合唱团还是参加学校排球队，游戏规则为：以0为起点， 第8页 | 共14页再从A，A ,A ,A ,A ,A ,A ,A （如图）这8个点中任取两点分别分终点得到两个向量， 1 2 3 4 5 6 7 8 记这两个向量的数量积为X。若X=0就参加学校合唱团，否则就参加学校排球队。 （1） 求小波参加学校合唱团的概率； （2） 求X的分布列和数学期望. 【学科网考点定位】该题主要考查离散型随机变量X的概率分布、期望，平面向量的概 念和运算，随机变量的概率等基础知识，考查综合分析能力和运算能力. 19（本小题满分12分） 如图，四棱锥P-ABCD中，PA⊥平面ABCD，E为BD的中点，G为PD的中点，△DAB ≌△ 第9页 | 共14页DCB，EA=EB=AB=1，PA= ，连接CE并延长交AD于F. （1） 求证：AD⊥平面CFG； （2） 求平面BCP与平面DCP的夹角的余弦值. 第10页 | 共14页20．（本小题满分13分） x2 y2 如图，椭圆C：  1(ab0)经过点P（1. ），离心率e= ，直线l的方程为x=4. a2 b2 (1)求椭圆C的方程； (2)AB是经过右焦点F的任一弦（不经过点P），设直线AB与直线l相交于点M，记PA， PB，PM的斜率分别为k ,k ,k .问：是否存在常数λ，使得k +k =k ？若存在， 1 2 3 1 2 3 第11页 | 共14页求λ的值；若不存在，说明理由. 直线方程表示斜率，通过化简求解. 【学科网考点定位】本题主要考查圆锥曲线的定义、标准方程、几何性质，直线与圆锥 曲线的交点等基础知识，考查分析问题、解决问题的能力，考查逻辑推理能力，推理论 证能力和计算能力. 21.（本小题满分14分） 1 已知函数 f(x)a(12 x ),a为常数且a＞0. 2 （2）证明：函数f（x）的图像关于直线x= 对称； （3）若x 满足f（f（x））= x 但f（x）≠x，则x 称为函数f（x）的二阶周期点， 0 0 0， 0 0 0 如果f（x）有两个二阶周期点x，x，试确定a的取值范围； 1 2 第12页 | 共14页（4）对于（2）中的x，x，和a，设x 为函数f（f（x））的最大值点，A（x，f（f 1 2 3 1 （x））），B（x，f（f（x））），C（x，0），记△ABC的面积为S（a），讨论S 1 2 2 3 （a）的单调性. 第13页 | 共14页第14页 | 共14页