数学（全国卷理科02）（考试版A3）_2024高考押题卷_62024学科网全系列_24学科网高考押题预测卷_2024年高考数学押题预测卷_数学（全国卷理科02）-2024年高考押题预测卷

……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ … ……………… 学 校 ： ______________ 姓 名 ： _____________ 班 级 ： _______________ 考 号 ： ______________________ 绝密★启用前 1 x2 f xcos2x  exex f(x) ln A． B． x x21 2024 年高考押题预测卷【全国卷 02】 exex x21 f(x) f(x)sin2xln 理科 数学 C． x D． x2  a    b  c 0  , a b 1,c  3   （考试时间：120分钟 试卷满分：150分） 5．已知平面向量a,b,c满足 ，则a与b 的夹角为（ ） 注意事项： π π 3 2 A． B． C． π D． π 1．答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。 4 3 3 4 2．回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦 1 2 6．已知 f x1在R上单调递增，且为奇函数.若正实数a，b满足 f a4 f b2，则  的最小值为 a b 干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。 （ ） 3．考试结束后，将本试卷和答题卡一并交回。 3 2 3 3   2  2 第一部分（选择题 共60分） A．4 2 B．4 C．32 2 D．2 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求 7．2024年3月16日下午3点，在贵州省黔东南苗族侗族自治州榕江县“村超”足球场，伴随平地村足球队在 的．  x1  对阵口寨村足球队中踢出的第一脚球，2024年第二届贵州“村超”总决赛阶段的比赛正式拉开帷幕.某校足球社 1．已知集合 A  x x3 0 ，Bx|log 2 (x1)3 ，则 � R AB（ ） 的五位同学准备前往村超球队所在村寨调研，将在第一天前往平地村、口寨村、忠诚村，已知每个村至少有一 位同学前往，五位同学都会进行选择并且每位同学只能选择其中一个村，若学生甲和学生乙必须选同一个村， 3,9 (1,9] (1,3] (1,3) A． B． C． D． 则不同的选法种数是（ ） 1i 2025 A．18 B．36 C．54 D．72 z  2．已知复数 1i ，则 z 的虚部为（ ） 2 1 sincos ,cossin cos22 8．已知 2 2，则 （ ） A．1 B．i C．1 D．i l m   l ∥ ml m 7 7 5 39 5 39 3．设 ， 是两条不同的直线， ， 是两个不同的平面，若 ， ，则“ ”是“ ”的   A．32 B． 32 C． 32 D． 32 （ ） asin0.5,b30.5,clog 0.5 a,b,c A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 9．已知 0.3 ，则 的大小关系是（ ） 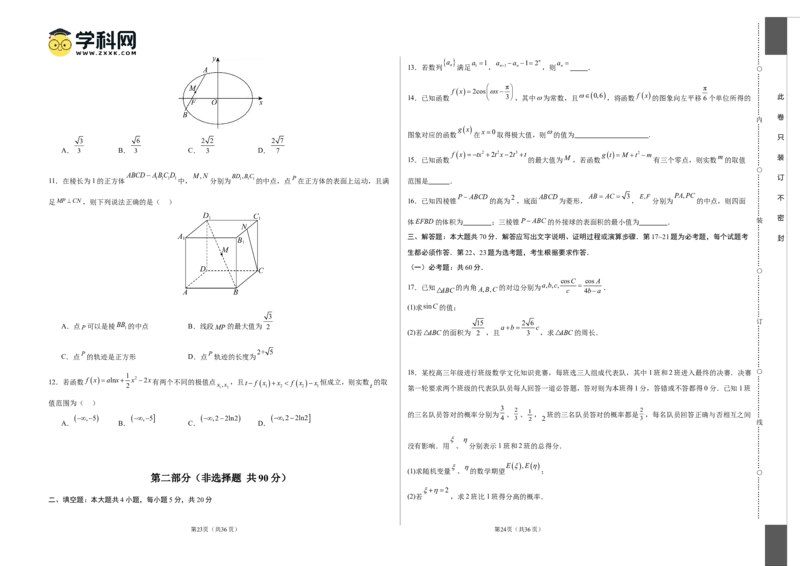4．已知函数 f(x)的图象如图所示，则函数 f(x)的解析式可能为（ ） A．abc B．cab C． acb D．cba x2 y2  1ab0 10．已知椭圆E：a2 b2 的左焦点为F ，如图，过点F 作倾斜角为60的直线与椭圆E交于A， 5 FM  OF B两点， M 为线段 AB 的中点，若 （ O 为坐标原点），则椭圆 E 的离心率为（ ） 第15页（共36页） 第16页（共36页） 学科网（北京）股份有限公司……………… ○ ……………… 外 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… ……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… a  a 1 a a 12n a  13．若数列 n 满足 1 ， n1 n ，则 n ．  π π 14．已知函数 f x2cos  x 3  ，其中为常数，且 0,6 ，将函数 f x 的图象向左平移6个单位所得的 此 卷 gx x0  图象对应的函数 在 取得极大值，则 的值为 . 只 3 6 2 2 2 7 A． 3 B． 3 C． 3 D． 7 15．已知函数 f xtx22t2x2t3t 的最大值为 M ，若函数 gtM t2m 有三个零点，则实数 m 的取值 装 11．在棱长为1的正方体 ABCDA 1 B 1 C 1 D 1中， M,N 分别为 BD 1 ,B 1 C 1的中点，点 P 在正方体的表面上运动，且满 范围是 ． 订 PABCD 2 ABCD AB AC  3 E,F PA,PC 不 足MPCN，则下列说法正确的是（ ） 16．已知四棱锥 的高为 ，底面 为菱形， ， 分别为 的中点，则四面 密 体EFBD的体积为 ；三棱锥PABC的外接球的表面积的最小值为 ． 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．第17~21题为必考题，每个试题考 封 生都必须作答．第22、23题为选考题，考生根据要求作答． （一）必考题：共60分． cosC cosA 17．已知 的内角 的对边分别为a,b,c,  ． ABC A,B,C c 4ba (1)求sinC的值； 3 A．点P可以是棱BB 1 的中点 B．线段MP的最大值为 2 15 ab 2 6 c (2)若ABC的面积为 2 ，且 3 ，求ABC的周长． 2+ 5 P P C．点 的轨迹是正方形 D．点 轨迹的长度为 18．某校高三年级进行班级数学文化知识竞赛，每班选三人组成代表队，其中1班和2班进入最终的决赛．决赛 1 12．若函数 f xalnx x22x有两个不同的极值点 ，且t f x x  f x x 恒成立，则实数 的取 2 x 1 ,x 2 1 2 2 1 t 第一轮要求两个班级的代表队队员每人回答一道必答题，答对则为本班得1分，答错或不答都得0分．已知1班 值范围为（ ） 3 2 1 2 的三名队员答对的概率分别为 、 、 ， 班的三名队员答对的概率都是 ，每名队员回答正确与否相互之间 ,5 ,5 ,22ln2 ,22ln2 4 3 2 2 3 A． B． C． D．   没有影响．用 、 分别表示1班和2班的总得分．   E,E (1)求随机变量 、 的数学期望 ； 第二部分（非选择题 共90分） 2 (2)若 ，求2班比1班得分高的概率． 二、填空题：本大题共4小题，每小题5分，共20分 第23页（共36页） 第24页（共36页）……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ … ……………… 学 校 ： ______________ 姓 名 ： _____________ 班 级 ： _______________ 考 号 ： ______________________ OO ABBA AA BB OO 19．如图，在圆柱 1中，一平面沿竖直方向截圆柱得到截面矩形 1 1，其中 1， 1为圆柱 1的母线，     点 C 在底面圆周上，且 BC 过底面圆心 O ，点D，E分别满足 A 1 D2DA,B 1 E 2EC ，过 DE 的平面与 BB 1交于点   BF FB(0) F ，且 1 . f xxex2ax(a0) 21．已知函数 ． (1)当2时，证明:平面DEF//平面ABC； e 10 (1)若函数 f x在 处的切线与坐标轴围成的三角形的面积为 ，求 的值； x1 2 a (2)若AA 2AB2AC,AF 与平面ABC所成角的正弦值为 10 ，求的值. 1 1 1 f x e a (2)若函数 的最小值为 ，求 的值． （二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题计分． 选修4-4：坐标系与参数方程 E D(1,0) x=1 E C xOy C 20．已知动圆 经过定点 ，且与直线 相切，设动圆圆心 的轨迹为曲线 . 22．已知在平面直角坐标系 中，以坐标原点O为极点，x轴的非负半轴为极轴建立极坐标系，曲线 1的极 (1)求曲线C的方程； (2)设过点 P(1,2) 的直线 l 1， l 2分别与曲线 C 交于 A ， B 两点，直线 l 1， l 2的斜率存在，且倾斜角互补，求证：直 坐标方程为 ；在平面直角坐标系 中，曲线 的参数方程为    xm 3cos （ 为参数），点 2sin xOy C 2 y 3sin  A 线AB的倾斜角为定值.  π  6,  的极坐标为 4且点A在曲线C 2 上. 第35页（共36页） 第36页（共36页） 学科网（北京）股份有限公司……………… ○ ……………… 外 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… ……………… ○ ……………… 内 ……………… ○ ……………… 装 ……………… ○ ……………… 订 ……………… ○ ……………… 线 ……………… ○ ……………… C C (1)求曲线 1的普通方程以及曲线 2的极坐标方程； (2)已知直线 l:x 3y0 与曲线 C 1 ,C 2分别交于 P ， Q 两点，其中 P ， Q 异于原点 O ，求 △APQ 的面积. 此 卷 只 装 订 选修4-5：不等式选讲 不 f x x  x2 xa 23．已知函数 . 密 f x14 封 a2 (1)当 时，求不等式 的解集； f x x28 x 16 (2)若 恒成立，求a的取值范围. 第43页（共36页） 第44页（共36页）