文档内容
2013年全国统一高考数学试卷(理科)(新课标Ⅱ)
一、选择题:本大题共12小题.每小题5分,共60分.在每个小题给出的四个
选项中,只有一项是符合题目要求的.
1.(5分)已知集合M={x|(x﹣1)2<4,x∈R},N={﹣1,0,1,2,3},则M
∩N=( )
A.{0,1,2} B.{﹣1,0,1,2}
C.{﹣1,0,2,3} D.{0,1,2,3}
2.(5分)设复数z满足(1﹣i)z=2i,则z=( )
A.﹣1+i B.﹣1﹣i C.1+i D.1﹣i
3.(5分)等比数列{a }的前n项和为S ,已知S =a +10a ,a =9,则a =(
n n 3 2 1 5 1
)
A. B. C. D.
4.(5分)已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n
,l⊄α,l⊄β,则( )
A.α∥β且l∥α B.α⊥β且l⊥β
C.α与β相交,且交线垂直于l D.α与β相交,且交线平行于l
5.(5分)已知(1+ax)(1+x)5的展开式中x2的系数为5,
则a=( )
A.﹣4 B.﹣3
C.﹣2 D.﹣1
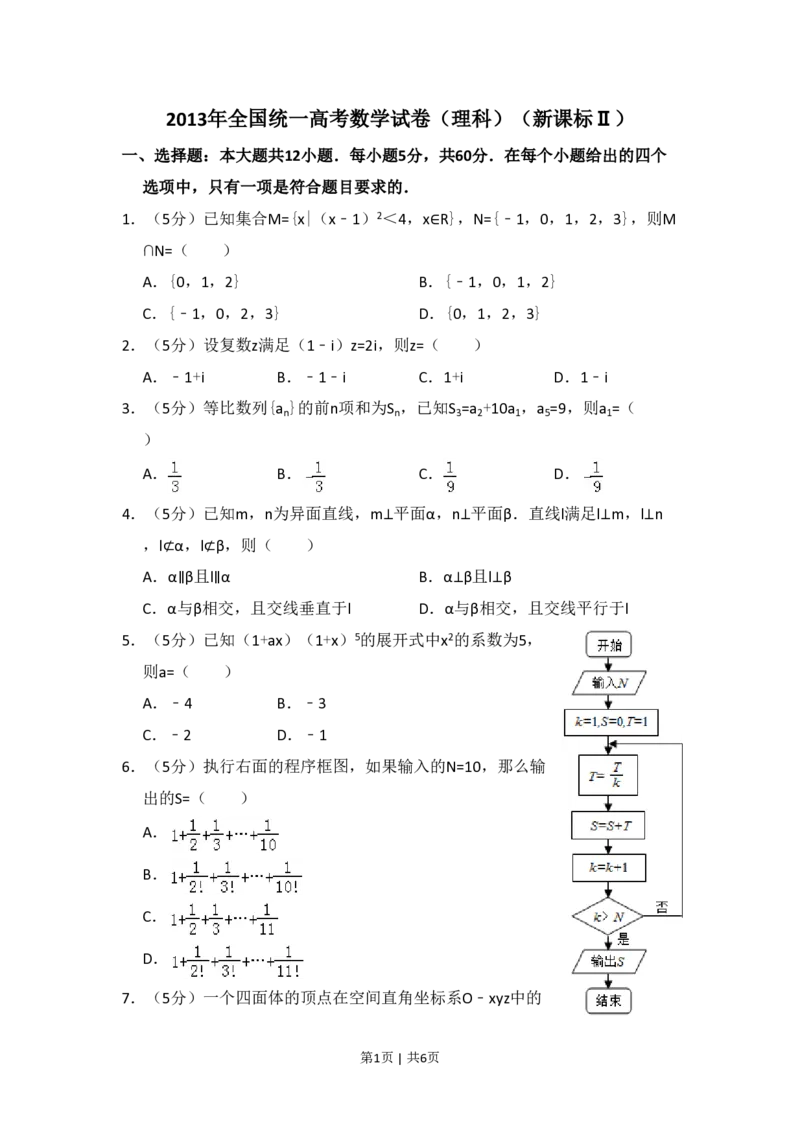
6.(5分)执行右面的程序框图,如果输入的N=10,那么输
出的S=( )
A.
B.
C.
D.
7.(5分)一个四面体的顶点在空间直角坐标系O﹣xyz中的
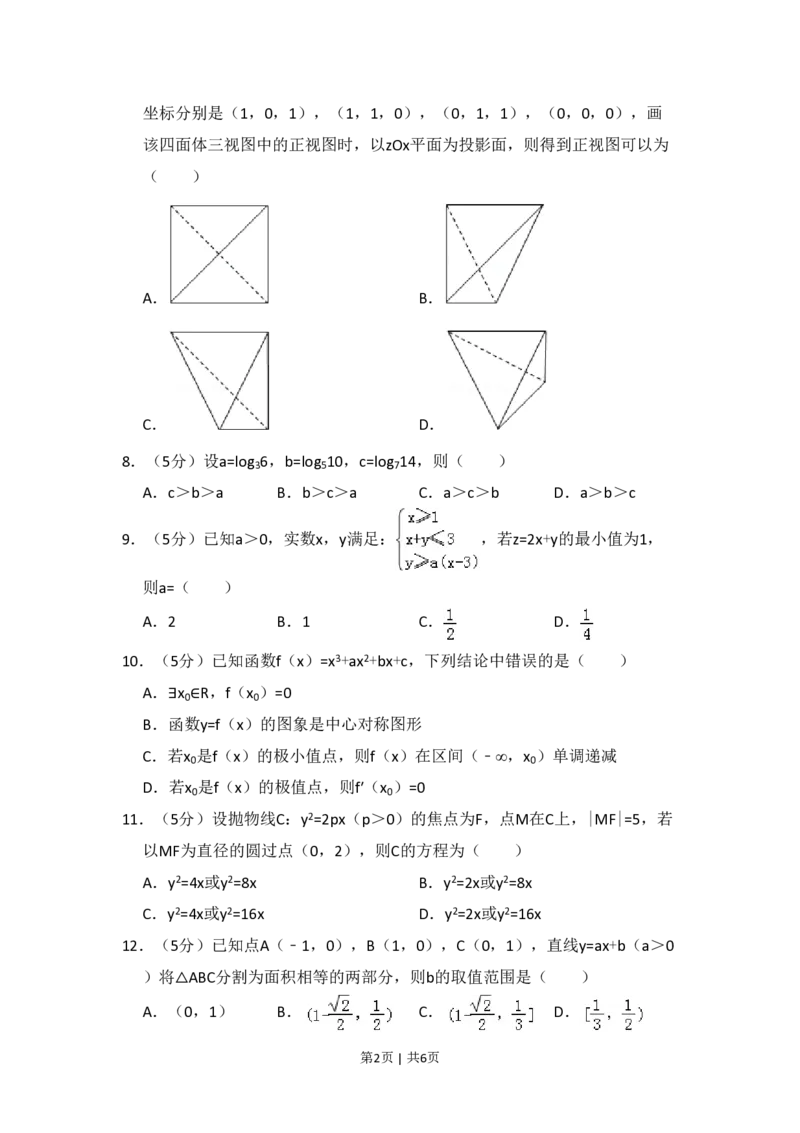
第1页 | 共6页坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画
该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为
( )
A. B.
C. D.
8.(5分)设a=log 6,b=log 10,c=log 14,则( )
3 5 7
A.c>b>a B.b>c>a C.a>c>b D.a>b>c
9.(5分)已知a>0,实数x,y满足: ,若z=2x+y的最小值为1,
则a=( )
A.2 B.1 C. D.
10.(5分)已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
A.∃x ∈R,f(x )=0
0 0
B.函数y=f(x)的图象是中心对称图形
C.若x 是f(x)的极小值点,则f(x)在区间(﹣∞,x )单调递减
0 0
D.若x 是f(x)的极值点,则f′(x )=0
0 0
11.(5分)设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若
以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
12.(5分)已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0
)将△ABC分割为面积相等的两部分,则b的取值范围是( )
A.(0,1) B. C. D.
第2页 | 共6页二、填空题:本大题共4小题,每小题5分.
13.(5分)已知正方形ABCD的边长为2,E为CD的中点,则 • = .
14.(5分)从n个正整数1,2,…,n中任意取出两个不同的数,若取出的两数
之和等于5的概率为 ,则n= .
15.(5分)设θ为第二象限角,若tan(θ+ )= ,则sinθ+cosθ= .
16.(5分)等差数列{a }的前n项和为S ,已知S =0,S =25,则nS 的最小值
n n 10 15 n
为 .
三.解答题:解答应写出文字说明,证明过程或演算步骤:
17.(12分)△ABC在内角A、B、C的对边分别为a,b,c,已知a=bcosC+csinB
.
(Ⅰ)求B;
(Ⅱ)若b=2,求△ABC面积的最大值.
18.(12分)如图,直棱柱ABC﹣A B C 中,D,E分别是AB,BB 的中点,AA =
1 1 1 1 1
AC=CB= AB.
(Ⅰ)证明:BC ∥平面A CD
1 1
(Ⅱ)求二面角D﹣A C﹣E的正弦值.
1
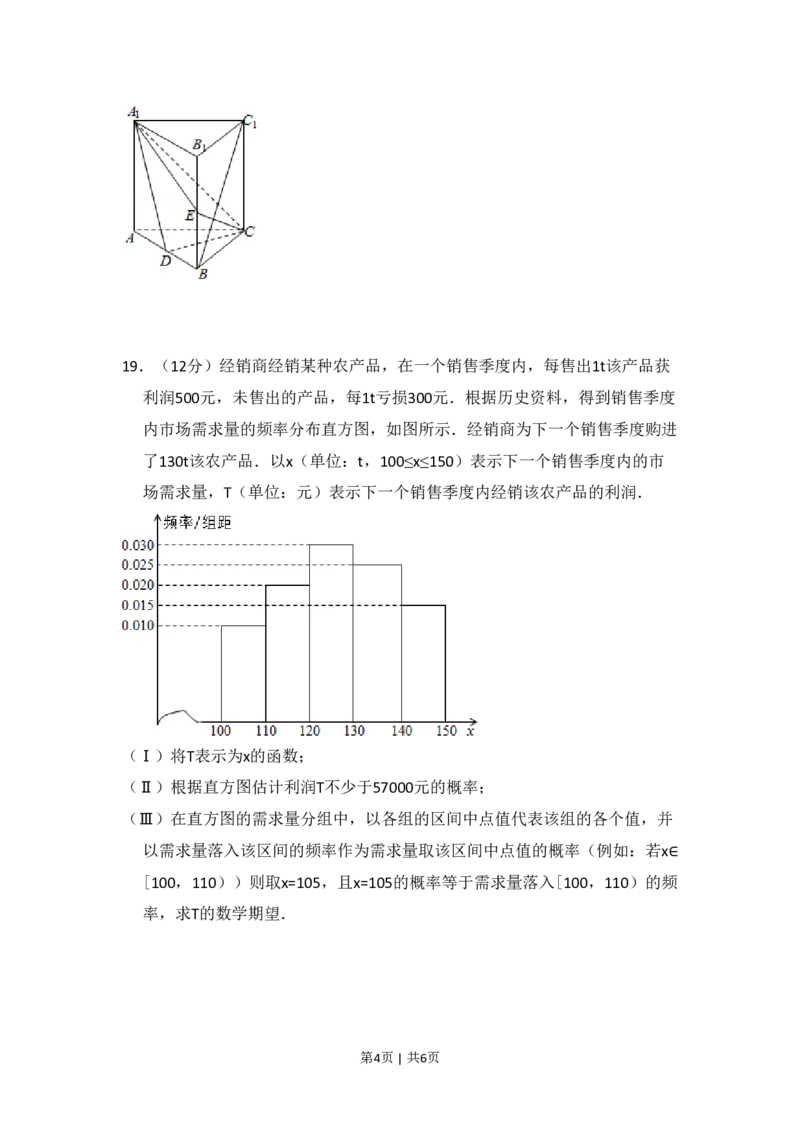
第3页 | 共6页19.(12分)经销商经销某种农产品,在一个销售季度内,每售出1t该产品获
利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度
内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进
了130t该农产品.以x(单位:t,100≤x≤150)表示下一个销售季度内的市
场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将T表示为x的函数;
(Ⅱ)根据直方图估计利润T不少于57000元的概率;
(Ⅲ)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并
以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈
[100,110))则取x=105,且x=105的概率等于需求量落入[100,110)的频
率,求T的数学期望.
第4页 | 共6页20.(12分)平面直角坐标系xOy中,过椭圆M: (a>b>0)右焦
点的直线x+y﹣ =0交M于A,B两点,P为AB的中点,且OP的斜率为 .
(Ⅰ)求M的方程
(Ⅱ)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面
积的最大值.
21.(12分)已知函数f(x)=ex﹣ln(x+m)
(Ι)设x=0是f(x)的极值点,求m,并讨论f(x)的单调性;
(Ⅱ)当m≤2时,证明f(x)>0.
第5页 | 共6页第6页 | 共6页