1_重庆市巴蜀中学2024届高考适应性月考卷（三）数学试题(1)_2023年10月_0210月合集_2024届重庆巴蜀中学高三适应性月考（三）_重庆巴蜀中学2024届高考适应性月考卷（三）数学

巴蜀中学 届高考适应性月考卷 三 2024 ( ) 数 学 注意事项： 1.答题前，考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上填写清楚. 2.每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净 后，再选涂其他答案标号.在试题卷上作答无效. 3.考试结束后， 请将本试卷和答题卡一并交回.满分150分， 考试用时120分钟. 一、单项选择题 (本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合 题目要求的) l.已知集合A={x|x=4k,k∈Z|,B={x|x=4m+1, m∈Z}, C=|x|x=4n+2, n∈Z|,D={x|x=4t+3, t∈Z}, 若a∈B,b∈C, 则下列说法正确的是 A.a+b∈A B.a+b∈B C.a+b∈C D.a+b∈D 2.已知a-b∈[5,27],a+b∈[6,30],则7a-5b的取值范围是 A.[-24,192] B.[-24,252] C.[36,252] D.[36,192] 3.已知函数 （ ＞ 恒过定点M(m,n),则函数 的图象不经过 A.第一象限 f x =Ba.ˣ 第 ⁻¹ 二 − 象 2 限 a C0.,a 第 ≠ 三 1 象 ) 限 D.第四象限 g x =m+xⁿ 4.已知非零向量石，b的夹角为2π/3，且满足( 则向量在向量b方向上的投影向量为 a+b ⊥a, 1 1 1 3 5.A已.−知 4 抛b物线CB:y.2²=b2px(p>0),C点.−M2 在b C上,直D.线−l： 2 b2x-y+6=0与x轴、y轴分别交于A，B两点，若△AMB 面积的最小值为, ,则p= 15 A.44 B.4 2 C.4或44 D.1或4 6. 把二项式 的所有展开项重新排列，记有理项都相邻的概率为p，有理项两两不相邻的概率为 8 1 q，则 x+x p A.5 q = B. C.4 D. 1 1 7.已知等差数列|aₙ|5的前n项和为Sₙ,对任意的n4∈N',均有 成立，则 的值的取值范围是 8 A.(3,+∞) B.[3,+∞) S₅≤ Sₙ 6 C.(-∞,-3)∪[3,+∞) D.(-∞,-3]∪[3,+∞) 8.已知函数f(x)的定义域为(0,+∞),导函数为f'(x),不等式 >xf(x)恒成立，且 则不 ' 7 等式 的解集为 x+1 2f x +xf x f 6 = 12, 3x+15 2 f x+4 < x+4 第1页共4页A.(-∞,4) B.(0,2) C.(-4,2) D.(-4,4) 二、多项选择题(本大题共４个小题，每小题５分，共20分，在每个给出的四个选项中，有多项是满足要求 的，全部选对的得５分，部分选对的得２分，有选错的得０分) 9.分别经过以下选项中的图象变换之后，能得到函数 的图象的是 π A.先将y=cosx的图象上各点的横坐标缩小为原来的y=再si将n图3x象−关 2 于x轴翻折 1 3, π B.先将y=sinx的图象上各点的横坐标缩小为原来的 ，再向右平移 个单位长度 1 3 6 π C.先将y=sinx的图象向右平移 个单位长度，再将各点的横坐标缩小为原来的 1 6 3 D.先将y=cosx的图象向左平移π个单位长度，再将各点的横坐标缩小为原来的 1 3 10.已知向量 其中a>0，b>0，则下列说法正确的是 1 1 A.若 ， m， =n可2以 a 作,n为 =平面 b4向量, 的一组基底，则log₂ab≠-3 B.若 则 C.若ma+b⊥=n1,, 则2²ᵃ⁺ᵇ有=最1 小值 D.若 则 m⋅n 6+4 2 b 7 11. 已知|定m义|=在|nR|>上4的函2,数f(ax∈)=x1sin2x-λcosx(λ>-1)，记f(x)在[-kπ，kπ](k∈N.)上的极值点为 共n个，则下列说法正确的是 x1,x2,⋯,xn(x1 < Ax.2n=<2⋯(k+<1)xn) B. C. 当 +1k==10 时,对任意λ>-1,x₁,x₂, ,x n 均为等差数列 D.当k=2时,存在λ>-1,使得x₁,x₂,…,x 为等差数列 n 12.已知函数 且a≠1)，则下列说法正确的是 |x| A.若函数yf=xf(x=)有a4个−零|lo点ga,|则x||0a1 D.当a>1时,函数y=f(x)有2个零点 三、填空题(本大题共4小题，每小题5分，共20分) 13.已知在等比数列|an|中,a₂,a₁₀是方程x²-13x+14=0的两个实数根，则a₆= . 14.已知F₁(0,-c),F₂(0,c)是双曲线E: 的下、上焦点，直线y=x+c与x轴交于A点，与双 2 2 y x 2 2 曲线的渐近线在第三象限内交于aB−点b，=且1 a 0,b> 0) 则双曲线的渐近线方程为 . F1 第F2 2 +页F1 共 B 4 =页2F1A,15. 已知函数 f(x)满足: ①f(x)的图象过点 ②f(x)是偶函数；③对任意的非零实数 3 请写出一个满足上8述 2 条;件的函数f(x)= . x1,x2,f x1 = x1 16. 在f三x2 角,x函 1,数x2 部,f分x2，=我f们x研 2 ,究过二倍角公式cos2x=2cos²x-1,我们还可以用类似方式继续得到三倍角公式.根 据你的研究结果解决如下问题：在锐角△ABC中，角 A，B，C的对边分别为 a, b, c,若 π 则 的取值范围是 . A≤ 3,cosC+ 3 1 四、解4co答s题A(−共37c0os分A，=解0,答应4写tan出A文+字tan说B明−A，证明过程或演算步骤) 17.(本小题满分10分) 2023年9月23 日，第19届亚洲运动会在杭州正式开幕.这是1990年第11届北京亚运会、2010年第16 届广州亚运会之后，中国第三次主办亚运盛会，也进一步激发了中国全民参与体育活动的热情. 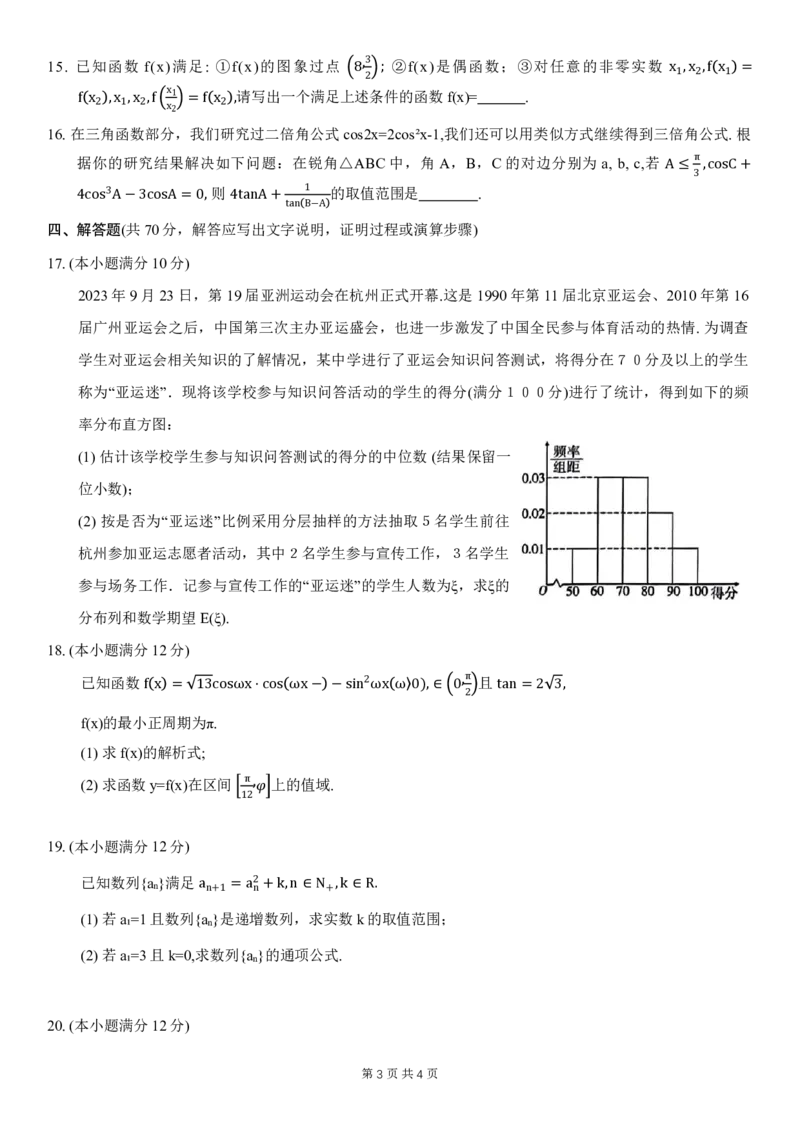为调查 学生对亚运会相关知识的了解情况，某中学进行了亚运会知识问答测试，将得分在７０分及以上的学生 称为“亚运迷”．现将该学校参与知识问答活动的学生的得分(满分１００分)进行了统计，得到如下的频 率分布直方图： (1) 估计该学校学生参与知识问答测试的得分的中位数(结果保留一 位小数)； (2) 按是否为“亚运迷”比例采用分层抽样的方法抽取５名学生前往 杭州参加亚运志愿者活动，其中２名学生参与宣传工作，３名学生 参与场务工作．记参与宣传工作的“亚运迷”的学生人数为ξ，求ξ的 分布列和数学期望E(ξ). 18.(本小题满分12分) 已知函数 且 2 π f x = 13cosωx⋅cos ωx− −sin ωx ω 0), ∈ 02 tan= 2 3, f(x)的最小正周期为π. (1)求f(x)的解析式; (2)求函数y=f(x)在区间 上的值域. π 12 19.(本小题满分12分) 已知数列{a }满足 n 2 (1)若a₁=1且数列{ a a n+ } 1 是=递a增 n+数k列,n，∈求N实 +,数k ∈ k R的. 取值范围； n (2)若a₁=3且k=0,求数列{a }的通项公式. n 20.(本小题满分12分) 第3页共4页已知△ABC的内角A,B,C所对的边分别为a,b,c, 2 (1)若b=2,求△ABC的面积; 2asinB= 3b,AC⋅AB=|AB| . (2) 若D为△ABC所在平面内一点,且D与B不在直线AC的同一侧,CD=3AD=6, 求四边形ABCD 面积 的最大值. 21.(本小题满分12分) 已知椭圆 C： 的上、下顶点分别为A, B, 左顶点为 D, △ABD是面积为 的正三角 2 2 x y 2 2 形. a +b =1 a b> 0) 3 (1)求椭圆C的方程; (2)过椭圆外一点M(m，0)的直线交椭圆于P，Q两点，已知点P与点P'关于x轴对称，直线P'Q与x轴 交于点K；若∠AKB是钝角，求m的取值范围. 22.(本小题满分12分) 已知函数 sinx (1)求证: f x = x时,,gf(x x )<=1;acosx. π (2)当 x ∈ 02 时,f(x)>g(x)恒成立,求实数a的取值范围; π π (3)当x ∈ −20 ∪ 02 时，[f(x)]²>g(x)恒成立，求实数a的取值范围. π π x ∈ −20 ∪ 02 第4页共4页