2024年高考数学试题（新课标II卷）_2024年高考真题卷_新课标Ⅱ卷（适用地区辽宁、重庆、海南、吉林、黑龙江、山西、云南、广西、甘肃、贵州、新疆）

2024年高考数学试题（新课标II卷） 一、选择题:本题共8小题，每小题5分，满分40分．每小题给出的四个选项中，只有一个是符合题意的. 1.已知z=-1-i ，则 z= A.0 B.1 C. 2 D.2 2.已知命题p:∀x∈R，x+1>1；命题q:∃x>0，x3=x，则 A.p和q都是真命题 B.¬p和q都是真命题 C.p和¬q都是真命题 D.¬p和¬q都是真命题 3.已知向量a，b满足: a=1，a+2b=2，且b-2a  ⊥b，则 b= 1 2 3 A. B. C. D.1 2 2 2 4.某农业研究部门在面积相等的100块稻田上种植新型水稻，得到各块稻田的亩产量(单位: kg )并部分 整理如下表所示. 亩产 [900，950) [950，1000) [1000，1050) [1050，1150) [1150，1200) 频数 6 12 18 24 10 根据表中数据，下列结论正确的是 A.100块稻田亩产量的中位数小于1050kg B.100块稻田中亩产量低于1100kg的稻田所占比例超过40% C.100块稻田亩产量的极差介于200kg到300kg之间 D.100块稻田亩产量的平均值介于900kg到1000kg之间 5.已知曲线C：x2+y2=16y>0  ，从C上任意一点P向x轴作垂线段PP，P为垂足，则线段PP的中 点M的轨迹方程为 x2 y2 A. + =1y>0 16 4  x2 y2 B. + =1y>0 16 8  y2 x2 C. + =1y>0 16 4  y2 x2 D. + =1y>0 16 8  6.设函数fx  =ax+1  2-1，gx  =cosx+2ax(a为常数)，当x∈-1，1  时，曲线y=fx  和y=gx  恰有一个交点，则a= 1 A.-1 B. C.1 D.2 2 52 7.已知正三棱台ABC-ABC的体积为 ，AB=6，AB =2，则AA与平面ABC所成角的正切值为 3 1 1 1 A. B.1 C.2 D.3 2 8.设函数fx  =x+a  lnx+b  ，若fx  ≥0，则a2+b2的最小值为 1 1 1 A. B. C. D.1 8 4 2 1二、选择题:本题共3小题，每小题6分，满分18分．每小题给出的备选答案中，有多个选项是符合题意 的．全部选对得6分，部分选对得3分，选错或不选得0分. 9.对于函数fx  =sin2x和gx  π =sin(2x- )，下列正确的有 4 A.fx  与gx  有相同零点 B.fx  与gx  有相同最大值 C.fx  与gx  有相同的最小正周期 D.fx  与gx  的图象有相同对称轴 10.抛物线C：y2=4x的准线为l，P为C上动点，过P作⊙A:x2+y-4  2=1的一条切线，Q为切点．过 P作C的垂线，垂足为B，则 A.l与⊙A相切 B.当P、A、B三点共线时，PQ= 15 C.当 PB=2时，PA⊥AB D.满足 PA= PB的点A有且仅有2个 11.设函数fx  =2x3-3ax2+1 ，则 A.当a>1时，fx  的三个零点 B.当a<0时，x=0是fx  的极大值点 C.存在a,b，使得x=b为曲线fx  的对称轴 D.存在a，使得点 1，f1    为曲线y=fx  的对称中心 三、填空题:本题共3小题，每小题5分，满分15分. 12.记S 为等差数列a n n  的前n项和，若a +a =7，3a +a =5 ，则S = . 3 4 2 5 10 13.已知α为第一象限角，β为第三象限角，tanα+tanβ=4，tanαtanβ= 2+1，则sinα+β  = . 14.在下图的4*4方格表中有4个方格，要求每行和每列均恰有一个方格被选中，则共有 种选法； 在符合上述要求的选法中，选中方格中的四个数之和的最大值是 . 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 四、解答题:本题共5小题，满分87分．解答应写出必要的文字说明、证明过程或演算步骤. 15.(本题满分13分)记△ABC的内角A,B,C的对边分别为a,b,c，已知sinA+ 3cosA=2. （1）求A； （2）若a=2， 2bsinC=csin2B ，求△ABC的周长. 216.(本题满分15分)已知函数fx  =ex-ax-a3. （1）当a=1时，求曲线y=fx  在点 1，f1    处的切线方程； （2）若fx  有极小值，且极小值小于0，求a的取值范围. 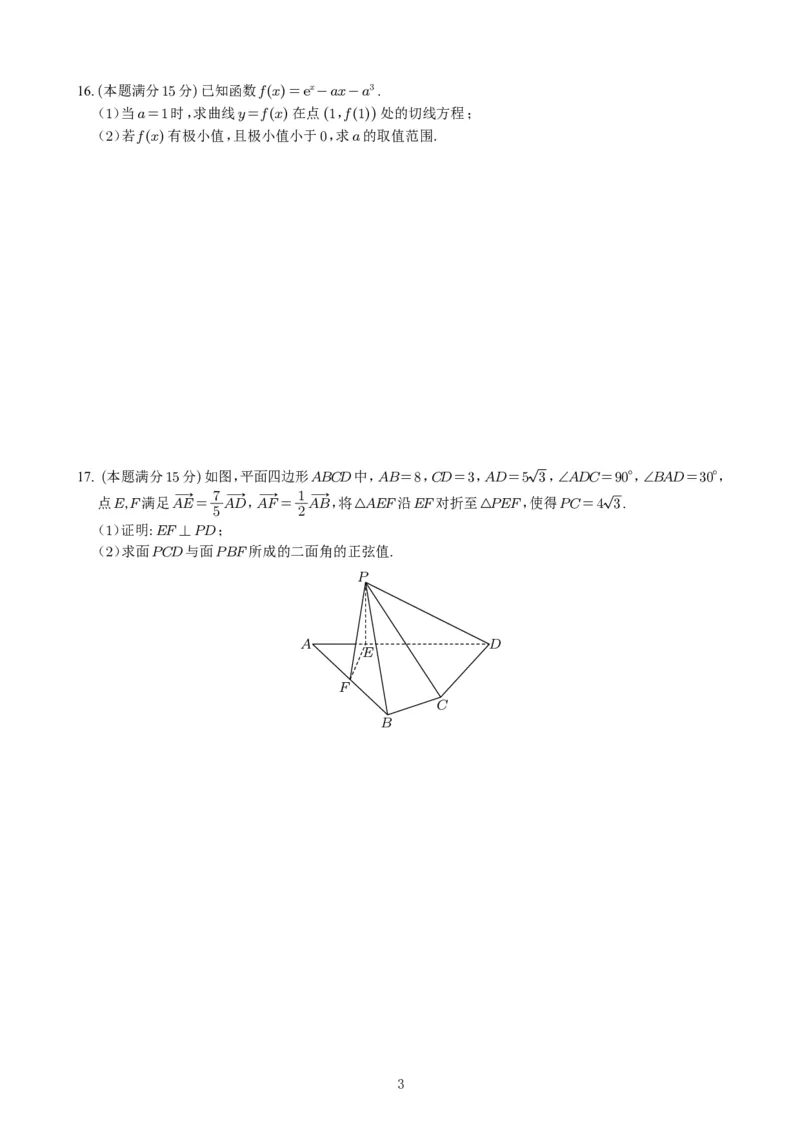17. (本题满分15分)如图，平面四边形ABCD中，AB=8，CD=3，AD=5 3，∠ADC=90°，∠BAD=30°，     7 1 点E,F满足AE= AD，AF= AB，将△AEF沿EF对折至△PEF，使得PC=4 3. 5 2 （1）证明:EF⊥PD； （2）求面PCD与面PBF所成的二面角的正弦值. P A D E F C B 318. (本题满分17分)某投篮比赛分为两个阶段，每个参赛队由两名队员组成，比赛具体规则如下:第一阶 段由参赛队中一名队员投篮3次，若3次都未投中，则该队被淘汰，比赛成绩为0分；若至少投中1次， 则该队进入第二阶段，由该队的另一名队员投篮3次，每次投中得5分，未投中得0分．该队的比赛成 绩为第二阶段的得分总和．某参赛队由甲、乙两名队员组成，设甲每次投中的概率为p，乙每次投中的 概率为q，各次投中与否相互独立. （1）若p=0.4，q=0.5，甲参加第一阶段比赛，求甲、乙所在队的比赛成绩不少于5分的概率； （2）假设00  ，点P 15,4  在C上，k为常数，0