文档内容
年广东省高考数学试卷(理科)
2013
一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的
.
1.(5分)(2013•广东)设集合M={x|x2+2x=0,x∈R},N={x|x2﹣2x=0,x∈R},则M∪N=( )
A {0} B {0,2} C {﹣2,0} D {﹣2,0,2}
. . . .
2.(5分)(2013•广东)定义域为R的四个函数y=x3,y=2x,y=x2+1,y=2sinx中,奇函数的个数是( )
A 4 B 3 C 2 D 1
. . . .
3.(5分)(2013•广东)若复数z满足iz=2+4i,则在复平面内,z对应的点的坐标是( )
A (2,4) B (2,﹣4) C (4,﹣2) D (4,2)
. . . .
4.(5分)(2013•广东)已知离散型随机变量X的分布列为
X 1 2 3
P
则X的数学期望E(X)=( )
A B 2 C D 3
. . . .
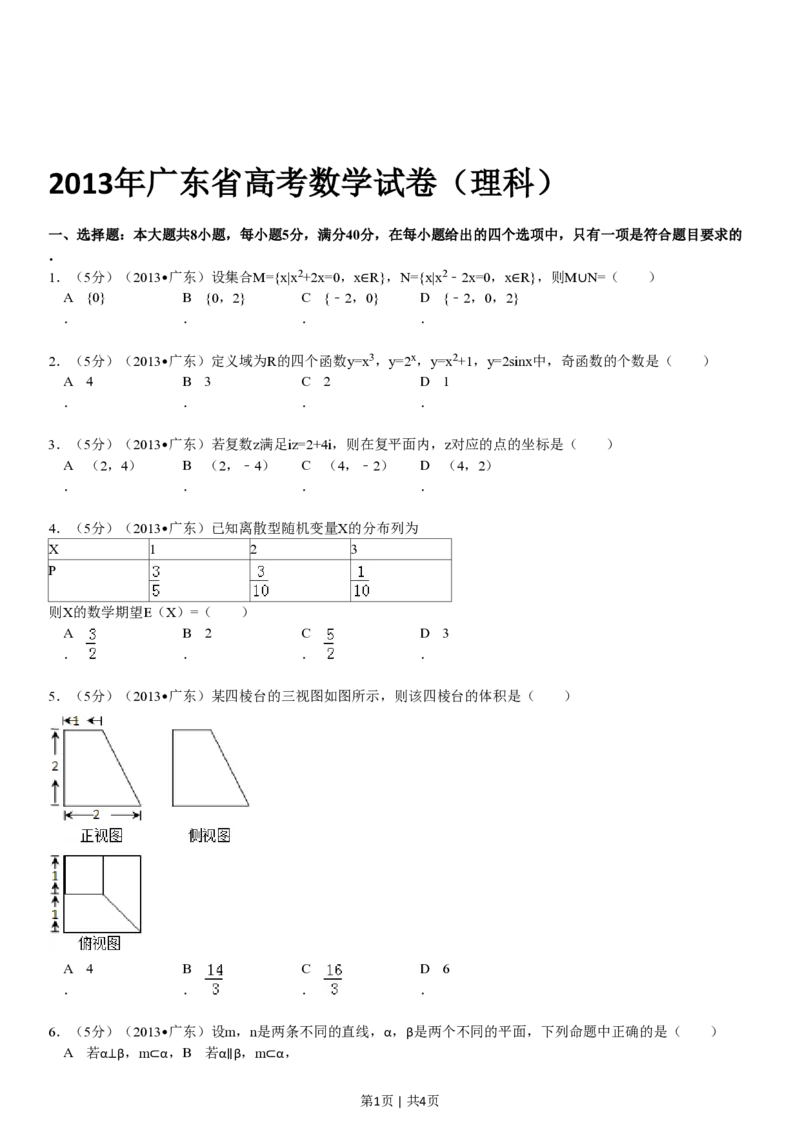
5.(5分)(2013•广东)某四棱台的三视图如图所示,则该四棱台的体积是( )
A 4 B C D 6
. . . .
6.(5分)(2013•广东)设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是( )
A 若α⊥β,m⊂α,B 若α∥β,m⊂α,
第1页 | 共4页. n⊂β,则m⊥n . n⊂β,则m∥n
C 若m⊥n,m⊂α D 若m⊥α,m∥n,
. ,n⊂β,则α⊥β . n∥β,则α⊥β
7.(5分)(2013•广东)已知中心在原点的双曲线C的右焦点为F(3,0),离心率等于 ,则C的方程是(
)
A B C D
. . . .
8.(5分)(2013•广东)设整数n≥4,集合X={1,2,3,…,n}.令集合S={(x,y,z)|x,y,z∈X,且三条件x
<y<z,y<z<x,z<x<y恰有一个成立}.若(x,y,z)和(z,w,x)都在S中,则下列选项正确的是(
)
A (y,z,w)∈SB (y,z,w)∈SC (y,z,w)∉ D (y,z,w)∉
. ,(x,y,w). ,(x,y,w). S,(x,y,w . S,(x,y,w
∉S ∈S )∈S )∉S
二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分.
9.(5分)(2013•广东)不等式x2+x﹣2<0的解集为 _________ .
10.(5分)(2013•广东)若曲线y=kx+lnx在点(1,k)处的切线平行于x轴,则k= _________ .
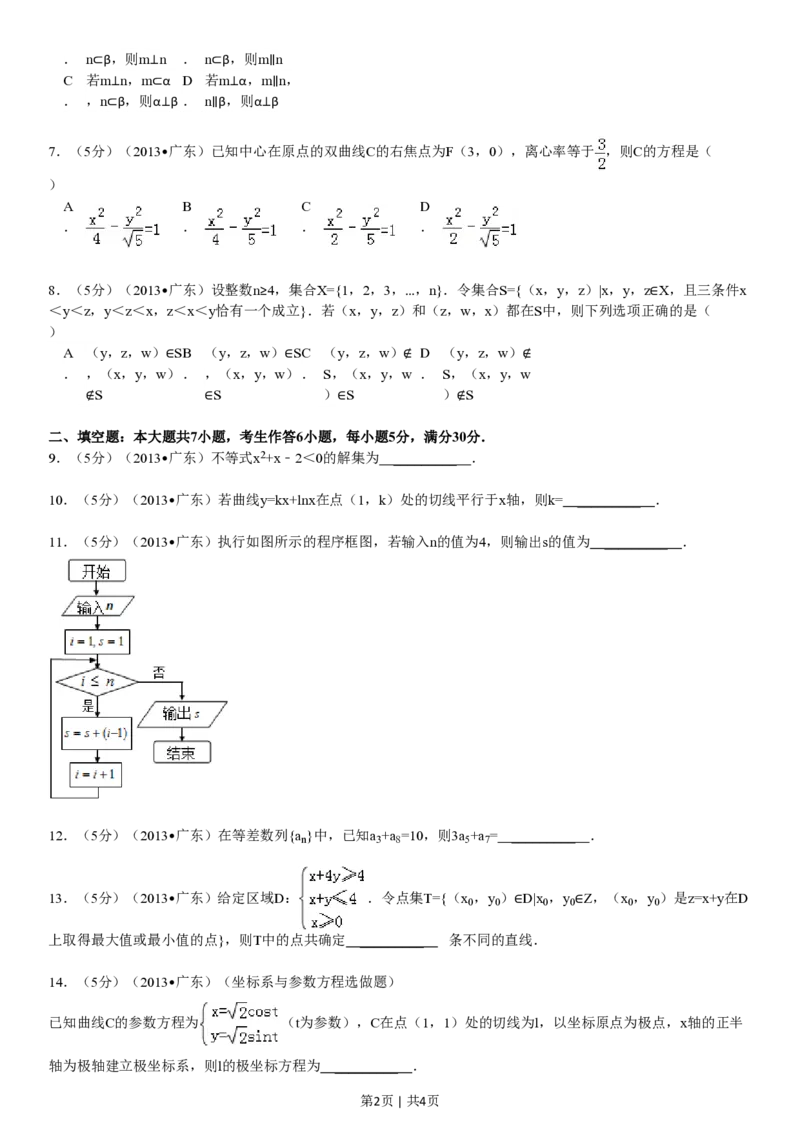
11.(5分)(2013•广东)执行如图所示的程序框图,若输入n的值为4,则输出s的值为 _________ .
12.(5分)(2013•广东)在等差数列{a }中,已知a +a =10,则3a +a = _________ .
n 3 8 5 7
13.(5分)(2013•广东)给定区域D: .令点集T={(x ,y )∈D|x ,y ∈Z,(x ,y )是z=x+y在D
0 0 0 0 0 0
上取得最大值或最小值的点},则T中的点共确定 _________ 条不同的直线.
14.(5分)(2013•广东)(坐标系与参数方程选做题)
已知曲线C的参数方程为 (t为参数),C在点(1,1)处的切线为l,以坐标原点为极点,x轴的正半
轴为极轴建立极坐标系,则l的极坐标方程为 _________ .
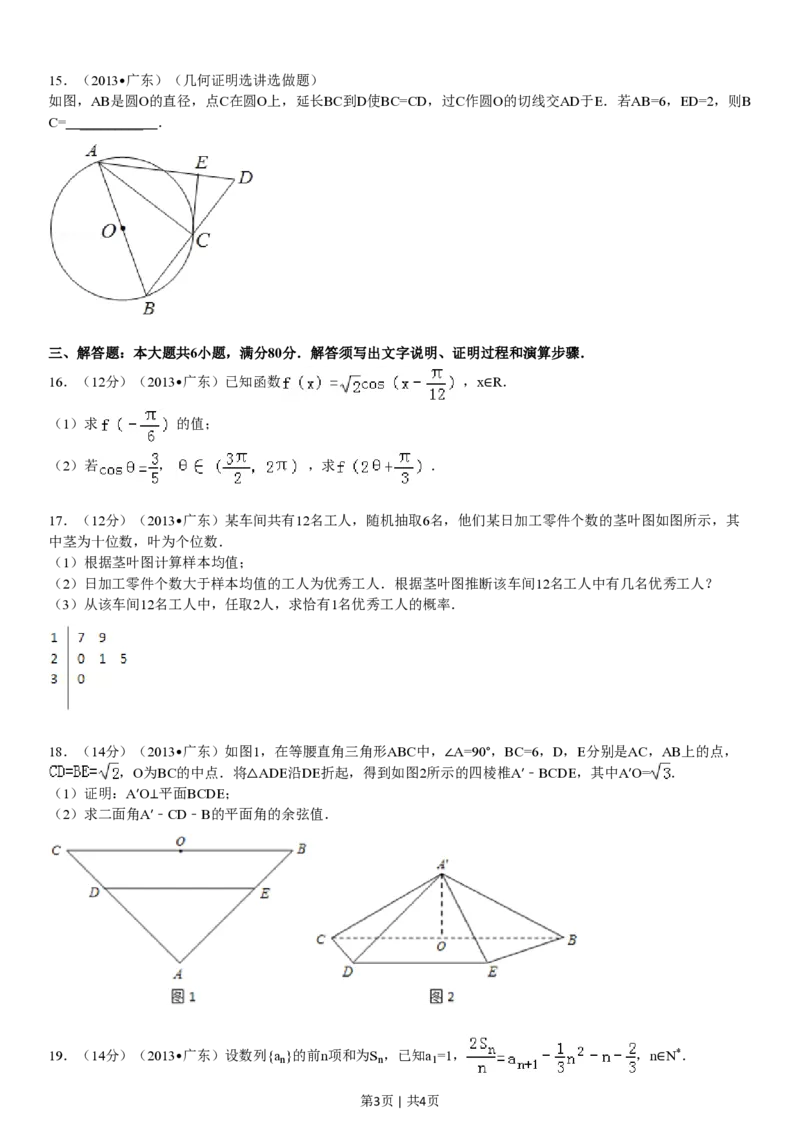
第2页 | 共4页15.(2013•广东)(几何证明选讲选做题)
如图,AB是圆O的直径,点C在圆O上,延长BC到D使BC=CD,过C作圆O的切线交AD于E.若AB=6,ED=2,则B
C= _________ .
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
16.(12分)(2013•广东)已知函数 ,x∈R.
(1)求 的值;
(2)若 , ,求 .
17.(12分)(2013•广东)某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其
中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)日加工零件个数大于样本均值的工人为优秀工人.根据茎叶图推断该车间12名工人中有几名优秀工人?
(3)从该车间12名工人中,任取2人,求恰有1名优秀工人的概率.
18.(14分)(2013•广东)如图1,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,
,O为BC的中点.将△ADE沿DE折起,得到如图2所示的四棱椎A′﹣BCDE,其中A′O= .
(1)证明:A′O⊥平面BCDE;
(2)求二面角A′﹣CD﹣B的平面角的余弦值.
19.(14分)(2013•广东)设数列{a }的前n项和为S ,已知a =1, ,n∈N*.
n n 1
第3页 | 共4页(1)求a 的值;
2
(2)求数列{a }的通项公式;
n
(3)证明:对一切正整数n,有 .
20.(14分)(2013•广东)已知抛物线C的顶点为原点,其焦点F(0,c)(c>0)到直线l:x﹣y﹣2=0的距离为
,设P为直线l上的点,过点P作抛物线C的两条切线PA,PB,其中A,B为切点.
(1)求抛物线C的方程;
(2)当点P(x ,y )为直线l上的定点时,求直线AB的方程;
0 0
(3)当点P在直线l上移动时,求|AF|•|BF|的最小值.
21.(14分)(2013•广东)设函数f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)当k=1时,求函数f(x)的单调区间;
(2)当 时,求函数f(x)在[0,k]上的最大值M.
第4页 | 共4页