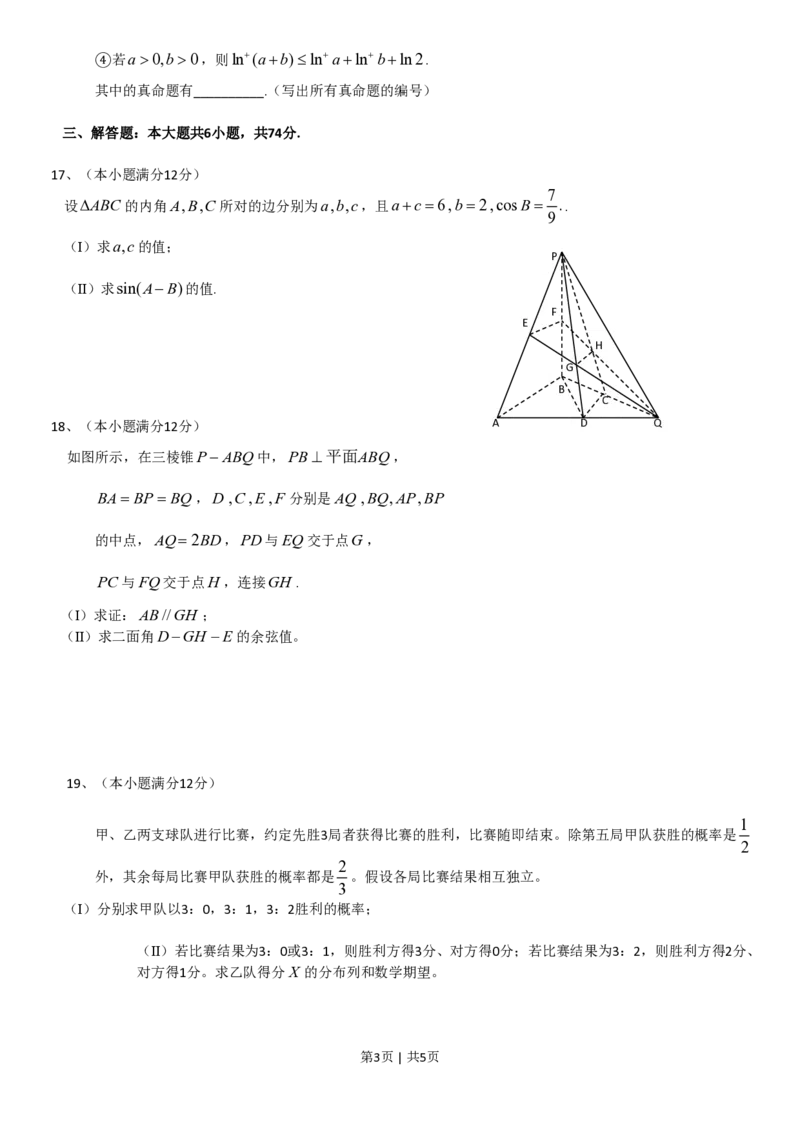文档内容
2013年普通高等学校招生全国统一考试(山东卷) 理 科 数 学
P(AB)= P(A)·P(B)
参考公式:如果事件A、B互斥,那么P(A+B)= P(A)+P(B) 如果事件A、B独立,那么 。
第Ⅰ卷(共60分)
一、选择题:本大题共12小题。每小题5分共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、复数z满组(z-3)(2-i)=5(z为虚数单位),则z的共轭复数z为
(A) 2+i (B) 2-i (C) 5+i (D) 5-i
2、已知集合A=0,1,2,则集合B= x- y xÎA,yÎA 中元素的个数是
(A) 1 (B) 3 (C) 5 (D) 9
1
3、已知函数 f(x)为奇函数,且当x>0时, f(x)= x2 + ,则 f(-1)=
x
(A) -2 (B) 0 (C) 1 (D) 2
9
4、已知三棱柱ABC-ABC 的侧棱与底面垂直,体积为 ,底面是边长为 3的正三角形,若P为底面
1 1 1 4
ABC 的中心,则PA与平面ABC所成角的大小为
1 1 1
5p p p p
(A) (B) (C) (D)
12 3 4 6
p
5、将函数y =sin(2x+j)的图象沿x轴向左平移 个单位后,得到一个偶函数的图象,则j的一个可能取值
8
为
3p p p
(A) (B) (C) 0 (D) -
4 4 4
ì2x- y-2³0,
ï
6、在平面直角坐标系xOy中,M 为不等式组íx+2y-1³0, 所表示的区域上一动点,则直线OM
ï
3x+ y-8£0
î
的斜率的最小值为
1 1
(A) 2 (B) 1 (C) - (D) -
3 2
7、给定两个命题 p,q. 若Øp是q的必要不充分条件,则 p是Øq的
(A) 充分不必要条件 (B) 必要不充分条件 (C) 充要条件 (D) 既不充分也不必要条件
8、函数y = xcosx+sinx的图象大致为
y y y y
p p p p
O x O x O x O x
第1页 | 共5页(A) (B) (C) (D)
9、过点(3,1)作圆(x-1)2 + y2 =1的两条切线,切点分别为A,B,则直线AB的方程为
(A) 2x+ y-3=0 (B) 2x- y-3=0 (C) 4x- y-3=0 (D) 4x+ y-3=0
10、用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为
(A) 243 (B) 252 (C) 261 (D) 279
1 x2
11、抛物线C : y = x2(p>0)的焦点与双曲线C : - y2 =1的右焦点的连线交C 于第一象限的点M. 若
1 2p 2 3 1
C 在点M 处的切线平行于C 的一条渐近线,则 p=
1 2
3 3 2 3 4 3
(A) (B) (C) (D)
16 8 3 3
xy 2 1 2
12、设正实数x,y,z满足x2 -3xy+4y2 -z =0.则当 取得最大值时, + - 的最大值为
z x y z
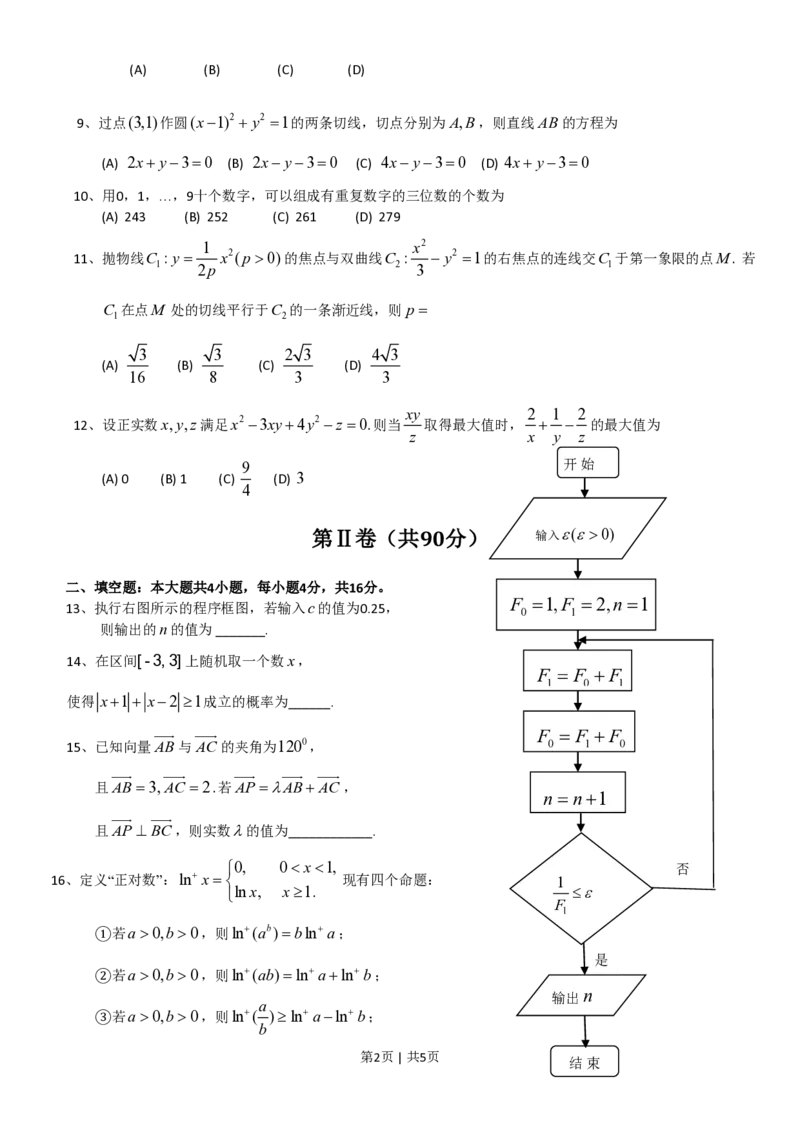
9 开 始
(A) 0 (B) 1 (C) (D) 3
4
第Ⅱ卷(共90分) 输入e(e>0)
二、填空题:本大题共4小题,每小题4分,共16分。
F =1,F = 2,n =1
13、执行右图所示的程序框图,若输入c的值为0.25,
0 1
则输出的n的值为_______.
14、在区间[-3,3] 上随机取一个数x,
F = F + F
1 0 1
使得 x+1+ x-2 ³1成立的概率为______.
uuur uuur F = F + F
15、已知向量AB与AC的夹角为1200, 0 1 0
uuur uuur uuur uuur uuur
且AB=3,AC =2.若AP=lAB+ AC,
n = n+1
uuur uuur
且AP^ BC,则实数l的值为____________.
ì0, 0< x<1, 否
16、定义“正对数”:ln+ x=í 现有四个命题: 1
îlnx, x³1. £e
F
1
①若a>0,b>0,则ln+(ab)=bln+ a;
是
②若a>0,b>0,则ln+(ab)=ln+ a+ln+b;
n
输出
a
③若a>0,b>0,则ln+( )³ln+ a-ln+b;
b
第2页 | 共5页
结 束④若a>0,b>0,则ln+(a+b)£ln+ a+ln+b+ln2.
其中的真命题有__________.(写出所有真命题的编号)
三、解答题:本大题共6小题,共74分.
17、(本小题满分12分)
7
设DABC 的内角A,B,C 所对的边分别为a,b,c,且a+c=6,b=2,cosB= ..
9
(Ⅰ)求a,c的值;
P
(Ⅱ)求sin(A-B)的值.
F
E
H
G
B
C
18、(本小题满分12分) A D Q
如图所示,在三棱锥P-ABQ中,PB^平面ABQ,
BA= BP= BQ,D ,C,E,F 分别是AQ ,BQ,AP,BP
的中点,AQ=2BD,PD与EQ交于点G,
PC与FQ交于点H ,连接GH .
(Ⅰ)求证:AB//GH ;
(Ⅱ)求二面角D-GH -E的余弦值。
19、(本小题满分12分)
1
甲、乙两支球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
2
2
外,其余每局比赛甲队获胜的概率都是 。假设各局比赛结果相互独立。
3
(Ⅰ)分别求甲队以3:0,3:1,3:2胜利的概率;
(Ⅱ)若比赛结果为3:0或3:1,则胜利方得3分、对方得0分;若比赛结果为3:2,则胜利方得2分、
对方得1分。求乙队得分X 的分布列和数学期望。
第3页 | 共5页20、(本小题满分12分)
设等差数列a 的前n项和为S ,且S =4S ,a =2a +1.
n n 4 2 2n n
(Ⅰ)求数列{a }的通项公式;
n
a +1
(Ⅱ)设数列{b }的前n项和为T ,且T + n =l(l为常数)。令c =2b ,(nÎN*),求数
n n n 2n n 2n
列{c }的前n项和R 。
n n
21、(本小题满分13分)
x
设函数 f(x)= +c(e=2.71828… 是自然对数的底数,cÎR)
e2x
(Ⅰ)求 f(x)的单调区间、最大值;
(Ⅱ)讨论关于x的方程 lnx = f(x)根的个数。
22、(本小题满分13分)
x2 y2 3
椭圆C: + =1(a>b>0)的左、右焦点分别是F ,F ,离心率为 ,过F 且垂直于x轴
a2 b2 1 2 2 1
的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P是椭圆C上除长轴端点外的任一点,连接PF ,PF 。设ÐFPF 的角平分线PM 交C
1 2 1 2
的长轴于点M(m,0),求m的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点。设直线
第4页 | 共5页1 1
PF ,PF 的斜率分别为k ,k ,若k ¹0,试证明 + 为定值,并求出这个定值.
1 2 1 2 kk kk
1 2
第5页 | 共5页